基于目标分流方法的船舶概念方案多学科设计优化
王健,谢伟,王涛,刘晓军
1中国舰船研究设计中心,湖北武汉430064
2江苏省特种设备安全监督检验研究院,江苏镇江212000
基于目标分流方法的船舶概念方案多学科设计优化
王健1,谢伟1,王涛1,刘晓军2
1中国舰船研究设计中心,湖北武汉430064
2江苏省特种设备安全监督检验研究院,江苏镇江212000
[目的]船舶概念设计是通过多个学科分析、协调从而得到综合优化概念方案的过程,也是一项技术难度大、涵盖范围广泛的复杂系统设计问题。同时,与船舶单个子学科技术的迅速发展相比,船舶总体设计优化方法发展相对缓慢。[方法]在阐述船舶分解与协调策略的基础上,采用解析目标分流方法(ATC),以某油船设计为例,建立由浮态与稳性、阻力与推进(快速性)、操纵性、舱容、经济性共5个学科组成的船舶概念设计优化数学模型,探讨船舶概念设计阶段的总体设计优化问题。[结果]数值算例表明,解析目标分流方法可以较好地解决船舶总体设计学科间复杂耦合所带来的计算困难,具有良好的稳定性与收敛性,[结论]可有效支撑船舶的总体设计优化。
解析目标分流法;多学科设计优化;分解协调策略;船舶概念设计
Abstract:[Objectives]Ship conceptual design requires the coordination of many different disciplines for comprehensive optimization,which presents a complicated system design problem affecting several fields of technology.However,the development of overall ship design is relatively slow compared with other subjects.[Methods]The decomposition and coordination strategy of ship design is presented,and the analytical target cascading(ATC)method is applied to the multidisciplinary design optimization of the conceptual design phase of ships on this basis.A tank ship example covering the 5 disciplines of buoyancy and stability,rapidity,maneuverability,capacity and economy is established to illustrate the analysis process in the present study.[Results]The results demonstrate the stability,convergence and validity of the ATC method in dealing with the complex coupling effect occurring in ship conceptual design.[Conclusions]The proposed method provides an effective basis for optimization of ship conceptual design.
Key words:analytical target cascading(ATC) method; multidisciplinary design optimization;decomposition and coordination strategy;ship conceptual design
0 引 言
舰船总体设计是一门综合集成技术,是舰船研制的核心技术[1-2],也是一个多特性平衡、多系统协同、多学科优化的复杂设计过程,而传统设计过程通常未充分考虑到复杂系统间的耦合效应,难以在较短的设计时间和全局设计空间内获得综合效能优化的方案。近年来,随着计算机技术的迅猛发展,面向复杂系统的多学科设计优化方法(Multidisciplinary Design Optimization,MDO)得到了广泛关注[3],如冯佰威等[4-5]围绕水面舰船的主船体型线开展了面向航行性能的多学科设计优化研究。然而,国内船舶多学科设计优化应用研究起步不久,所探讨MDO方法的种类较为集中,对新型MDO方法的研究较少。其中,解析目标分流方法(Analytical Target Cascading,ATC)[6-8]作为一种基于多层级模型框架、并行设计思想的多学科优化设计方法,在飞机、汽车等复杂系统设计方面表现卓越,逐渐引起国内外工程师和学者的广泛关注。为分析ATC方法在船舶总体设计中的适用性和有效性,本文将某油船的概念设计简化为由浮态与稳性、阻力与推进(快速性)、操纵性、舱容、经济性5个学科组成的多学科设计问题,建立基于ATC方法的概念设计数学模型,并进行优化。
1 船舶多学科设计优化
1.1 船舶总体设计的分解与协调
船舶总体设计涉及的变量、学科、约束、目标等因素众多,为了减少复杂性和便于并行设计,通常需要对涉及的内容或按研制过程进行分解,建立各环节的相互联系,明确各自的责任、需求与目标。执行基于分解的设计优化通常需要两个步骤:首先,定义系统分解结构;其次,建立协调子系统间矛盾的求解策略。依据子系统间数据信息接口组成的不同,将复杂系统分为层次系统和非层次系统。其中,层次性系统的子系统之间没有信息交换,组织框架表现为树状结构;非层次系统的子系统信息可能存在交互或耦合作用,其组织框架表现为网状结构,如图1和图2所示。
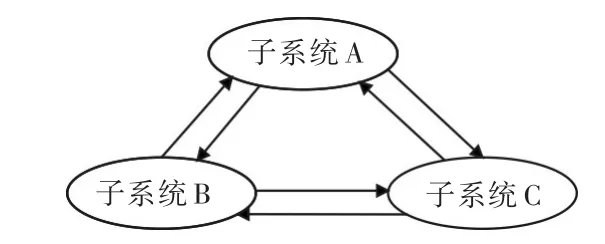
图1 非层次系统Fig.1 Non-hierarchic system
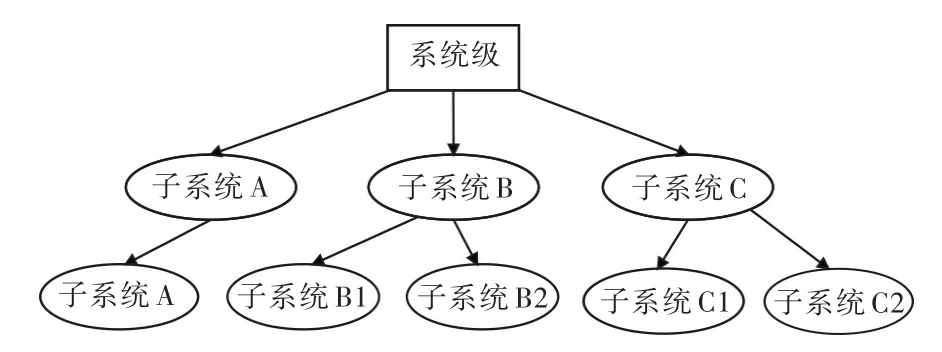
图2 层次系统Fig.2 Hierarchic system
总体设计协调是指依据合理的分解结构,通过耦合的设计参数将各子系统的相互作用有序联系和协同,使之为实现总体优化而服务的过程。针对众多的总体设计优化需求,需将这些分散的优化目标进行分类、重组,以有利于更合理、高效地开展总体设计的组织、协调与优化设计。图3所示为船舶总体设计经过分解与协调后,重组为船型设计、重量重心、使用效能和经济费用4个子系统的求解优化结构。
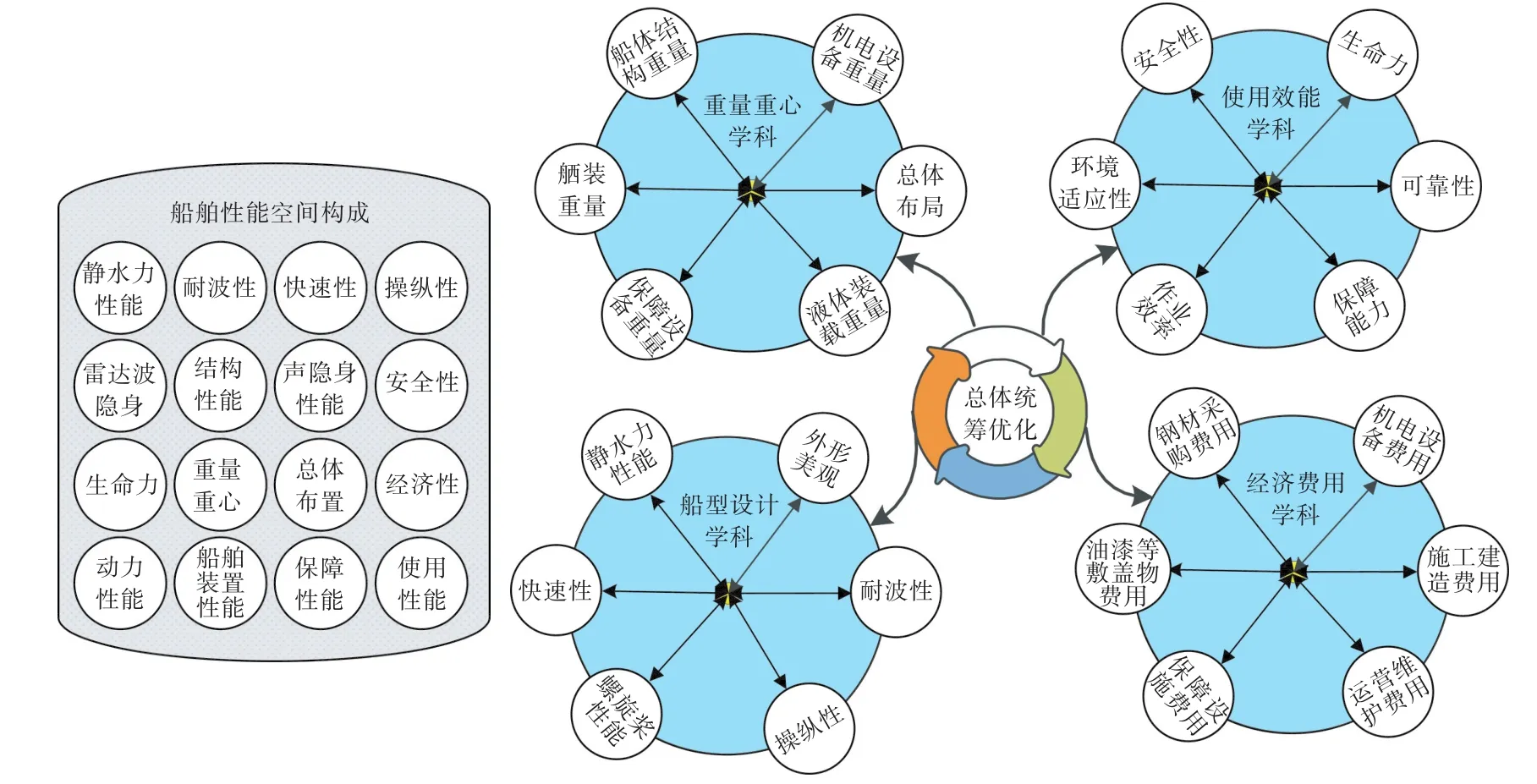
图3 船舶总体设计分解后的协同框架Fig.3 Coordination framework of overall ship design
协调策略中一个重要的方面是各子问题的求解顺序,以及耦合参数的传递顺序。通常对于不同的船舶总体设计分解结构,对应采用不同的协调策略。对非层次系统,所有的子系统在同一层次通过耦合变量互相联系;对层次系统,上层次各个系统可分解成下层次的一组子系统,同层次的子系统间共享若干变量或状态参数,协调通常是通过子系统与其上层系统之间交换数据来实现的。对此,不仅需要建立目标分解、逐层分流的正向优化流程,还需要建立子系统到系统、系统到总体的一致性反馈流程,以实现舰船总体设计方案的整体协调与优化,如图4所示。
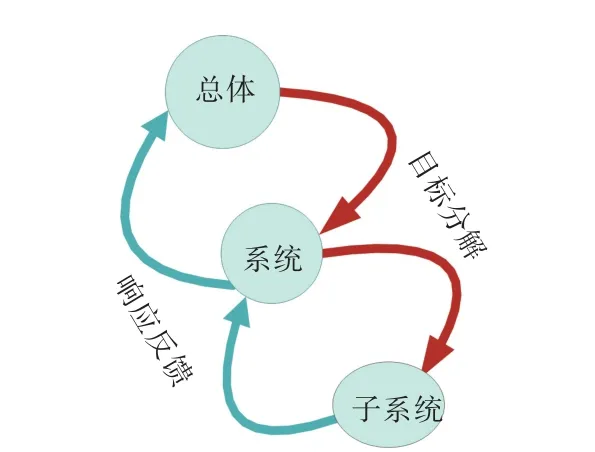
图4 目标分解与协调Fig.4 Target cascading and coordination
1.2 多学科设计优化方法
MDO方法来源于对复杂系统求解优化过程的思考与探索,该方法通过建立合适的系统分解结构、信息交互结构、计算分析与反馈结构等,结合搜索算法,以解决复杂耦合系统的综合优化问题。与传统的设计优化方法相比,MDO方法主要有以下特点:
1)充分利用不同学科间的耦合效应,以获得整体性能最优的设计方案;
2)将复杂工程分解为不同子系统的设计,实现并行设计,缩短设计周期;
3)采用高效的求解策略,组织子系统之间的数据传递和信息交流,在协调解决学科间一致性问题的同时,获得全局优化解。
按照MDO组织结构形式的不同,可分为单级优化方法和多级优化方法。其中,单级优化方法仅在系统层进行优化求解,子系统级只负责分析或计算;多级优化方法中各子系统层可相对独立地进行优化分析,系统层主要负责各系统优化结果的协调与控制。常用的多级优化方法有:协同优化(Collaborative Optimization,CO)[9]、并行子空间优化(ConcurrentSubspace Optimization,CSSO)[3]、二级系统一体化合成优化(Bi-Level Integrated System Synthesis,BLISS)[10]等。
2 目标分流方法的基本原理
2.1 ATC优化求解流程
ATC方法的思想是将复杂的系统设计问题逐层分解,形成基于面向目标的层级组合,通过由上至下逐层分解目标的过程,将总体目标期望传递给各级层次的子系统,各子系统以总体分配的目标值开展并行优化。
ATC上层系统的性能目标值一旦确定,其下层各级元素的子目标值可通过逐级转换得到,其中,每个系统单元包括分析和优化两个模型。对于由总体层、系统层和子系统层组成的三层次框架,作为中间层的系统层同时接受总体层的分析信息和子系统反馈的优化信息,并在其分析与优化过程中将这些信息作为设计参数,中间层优化得到的结果将作为设定的目标值传递给子系统,同时作为性能函数的输出反馈给总体层。当总体层、系统层及子系统层之间的输入和输出间的偏差达到设计要求时,停止迭代。其目标分解过程如图5所示。
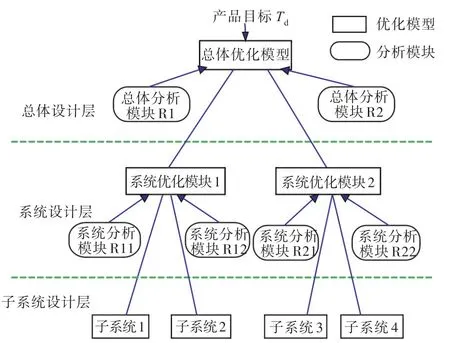
图5 基于ATC的产品层次分解结构Fig.5 Allocation structure of ATC hierarchy element
2.2 ATC的数学模型
在ATC结构中,对于第i层、第j单元的求解优化单元pij,由第i-1层给定响应目标值和联系变量的目标值,通过与该层次求解得到的响应目标值相比较,并以两者之间的偏差最小作为优化的目标,其响应协调的相应参数信息流如图6所示。
以单元pij为例,ATC通过引入与其上层父单元之间的耦合变量tij和响应变量rij,以实现各层之间解耦和各单元独立求解。当响应变量与原目标问题满足一致约束时,可保障目标分解问题的协调一致,如式(1)所示。

式中,cij为约束,表示第i层、第j单元的目标值与响应值的非一致性。对于由N个层级,共计M个单元所组成的目标分流结构,其一次性整体优化(All-in-one,AIO)数学模型如式(2)所示。
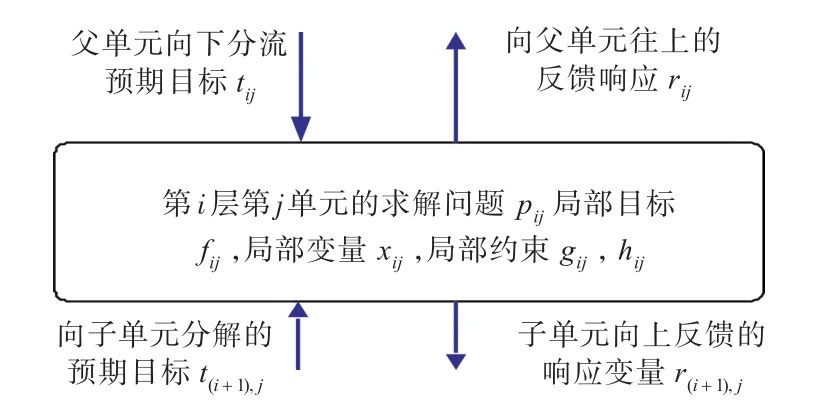
图6 单元pij响应协调的参数信息流向示意图Fig.6 Information flow of ATC elementpij
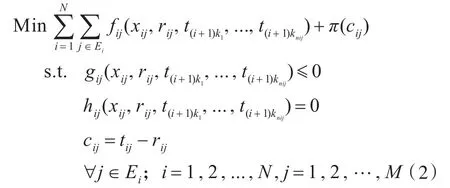
式中:fij,xij,gij,hij分别为第i层、第j单元的目标函数、设计变量、不等式约束和等式约束;Ei表示第i层中全部求解优化单元的集合。其中,总体层优化问题以达到产品预期为目标,并收集整个系统的相关信息,尽量减少总体层与系统层的偏差。总体层优化问题的数学模型如下:
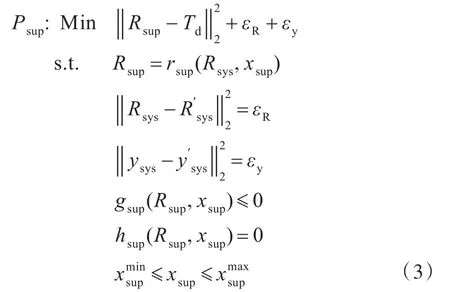
式中:Td为设计目标;Rsup为总体层目标响应值;rsup为总体层目标响应值的求解函数;xsup为总体层的设计变量;εR为系统层的响应偏差;εy为系统层耦合变量偏差;Rsys为系统层目标响应值;为总体层向系统层分解提出的目标值;为总体层耦合变量;ysys为系统层耦合变量;gsup为总体层的不等式约束;hsup为总体层的等式约束。
2.3 ATC的一致性约束方法
最初,ATC采用二次罚函数(Quadratic Penalty Function,QPF)对一致性约束进行松弛,后来,Lassiter采用普通拉格朗日函数(Ordinary Lagrangian Function,OLF)松弛,Kim和Tosserams采用增广拉格朗日函数(Augmented Lagrangian Function,ALF)松弛,从而产生了3种不同的ATC公式。
1)使用QPF的一致性松弛函数用式(4)表示,权重系数用式(5)更新。
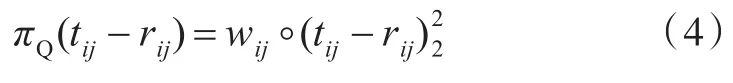
式中:wij为权重;符号◦表示Hadamard乘积;πQ为二次罚函数。

式中:β为步长;上标k为迭代次数。
2)采用OLF的一致性松弛函数用式(6)表示,拉格朗日乘子用式(7)所示的次梯度方法更新。
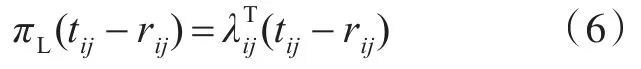
式中:λij为拉格朗日乘子;πL为基于拉格朗日函数松弛的罚函数。
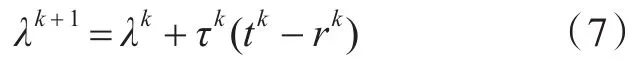
式中:τ为步长。
3)采用ALF的一致性松弛函数用式(8)表示,拉格朗日乘子用式(9)更新。
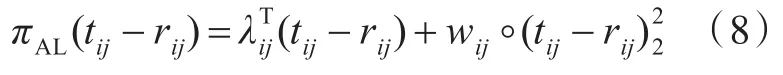
式中,πAL为基于增广拉格朗日函数松弛的罚函数。
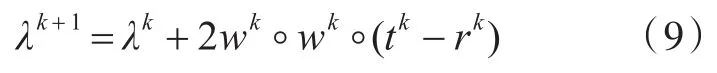
3 面向船舶概念设计的ATC优化方法
3.1 某船舶概念方案设计问题
一艘载重35 000 DWT的油船,主机功率Ps为7 860 kW,转速为123 r/min,球艏中心至龙骨的高度4 m,附体湿表面50 m2,球艏横剖面面积20 m2,艉横剖面面积16 m2,采用B系列螺旋桨,单桨,敞水式艉部,矩形舵板。
优化问题:以经济性为优化目标进行概念设计,优化主尺度与船型参数。需求解共计14个设计参数,分别为:船长L、船宽B、型深D、吃水T、方形系数CB、横剖面系数Cm、水线面系数Cwp、浮心纵向位置LCB、设计航速Vs、螺旋桨盘面比AE/Ao、螺旋桨螺距比p/Dp、螺旋桨直径Dp、舵面高度hR、舵面宽度bR。
3.2 概念设计的各学科简化模型
根据船舶总体概念设计的流程,按照多学科设计优化的思路,给出该油船总体概念设计阶段的框架。船舶多学科优化框架包括系统层和子系统层,共包括了浮态与稳性、阻力与推进、操纵性、舱容、经济性等学科,各学科的数学模型如下。
1)浮态与稳性学科。
对船舶设计而言,首先要保证浮态与稳性。一般来说,船舶浮态与稳性学科分析包括以下3方面内容:
(1)排水量Δ与船舶重量W的一致性约束,即Δ=W。
(2)初稳性高GM的约束,在概念设计阶段,其一般要求为GM≥0.04B。
(3)横摇周期Ts的约束,一般要求:Ts≥8.5 s。
其中,船舶重量由空船重量与载重量两部分组成,空船重量WL可依据经验公式,分为船体钢材、舾装设备和机电设备3个类型,分别估算得到。
船体钢材重量可按式(10)进行估算。
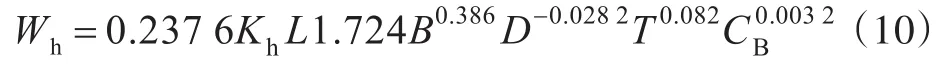
式中,Kh为船体结构形式对钢材重量的影响系数,取Kh=1。
舾装设备重量可按式(11)进行估算。
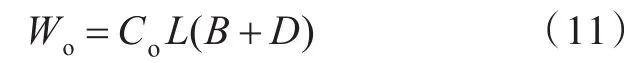
式中,Co=0.342 8(DWT×10-4)-1.495+0.088 6,其中DWT为载重量。
机电设备重量可按式(12)进行估算。
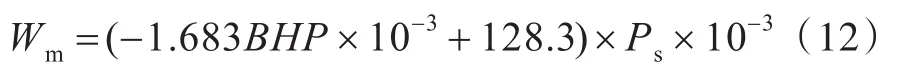
式中,Ps为主机功率,kW。
设计状态的初稳性高GM可按式(13)进行计算。
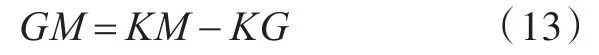
式中,KM和KG分别由式(14)和式(15)估算得到。
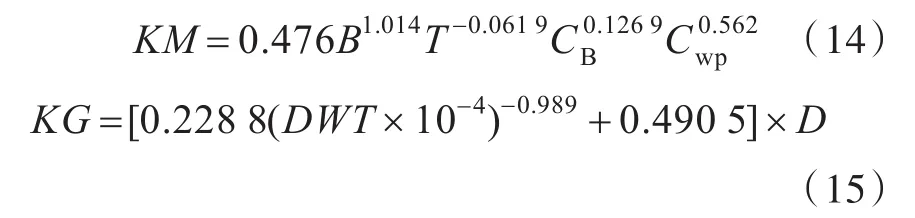
2)阻力与推进学科。
船舶阻力与推进学科包括以下3方面内容:
(1)船舶阻力RT与螺旋桨推力Tprop的平衡;
(2)螺旋桨转矩KQ的平衡;
(3)螺旋桨空泡的约束。
其中,船舶阻力RT可采用Holtrop公式(式(16))进行估算。
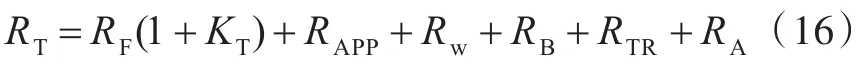
式中:RF为摩擦阻力;(1+KT)为船型系数;RAPP为附体阻力;RW为兴波和破波阻力;RB为球艏附加阻力;RTR为船艉附加粘压阻力;RA为船模修正阻力。
螺旋桨的推进效率由敞水效率、相对旋转效率、船身效率和轴系效率共同决定。系数KT和KQ可采用上海交通大学AU型螺旋桨回归公式(式(17)和式(18))进行估算。

式中:J为进速系数;Aijk,Bijk为计算系数。
3)操纵性学科。
在船舶概念设计阶段,重点分析直线稳定性和回转性能两个指标。其中,直线稳定性的无因次衡准指数C′可按式(19)进行估算,回转性无因次指标D′按式(20)进行估算,并需满足以下约束条件:0.002<C′<0.02,0<D′<4.0。

对于敞水式艉部船舶,相对回转直径可采用Lyster和Knights回归公式(式(20))进行估算。矩系数;
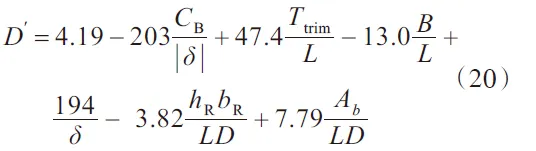
式中:δ为舵角;Ab为球艏浸湿面积;Ttrim为纵倾值。
4)舱容学科。
舱容学科设计的要求为新船所能提供的容积VH等于或大于新船所需舱容Vo,即

新船所需舱容为货油舱、专用压载水舱、污油舱、艏尖舱等舱所需体积之和,可按式(22)计算:
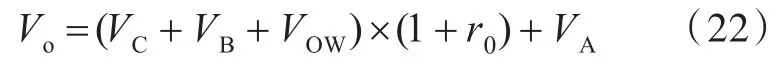
式中:VC为货油舱所需容积,按载运的货油量WC及货油比重确定,WC=DWT(1-KP),其中,KP=2.112×10-6×R+1.981×10-10×R2,R为续航力;VB为专用压载水舱所需容积,VB=P1×VC,其中P1=527DWT0.0501;VOW为污油舱所需容积,不小于货油舱容积的2%~3%;VA为其他舱室容积,取货油舱容积的2%~3%;r0为结构构件所占据的容积修正系数,在0.02~0.03范围内。
新船所能提供的容积可根据船的主尺度进行估算,如式(23)所示。

式中:CBD为计算到型深的方形系数;D1为计入舷弧和梁拱的相当型深。
5)经济性学科。
船舶的营运费用包括建造费用和使用维护费用2部分,本文仅针对建造费用进行分析。采用分项经费估算方法,针对船体钢材、舾装设备和机电设备3大项,依据分类的重量估算结果,按单位重量价格进行估算,如式(24)所示。
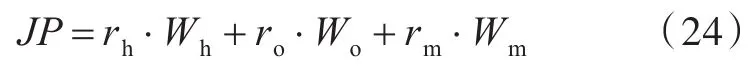
式中:rh,ro,rm分别为船体钢材、舾装设备和机电设备的单位重量价格,万元;Wh,Wo,Wm分别为钢材、舾装设备和机电设备的重量。
3.3 基于ATC的船舶概念设计方法
按照多学科协同优化设计思路,将船舶概念设计分为以船舶造价为系统控制层,协调浮态与稳性、舱容、阻力和推进、操纵性4个子学科。
各学科主要设计参数与约束如表1所示。

表1 各学科设计参数与约束Table 1 The design variable and constraint of disciplines
船舶概念设计多学科优化框架如图7所示。
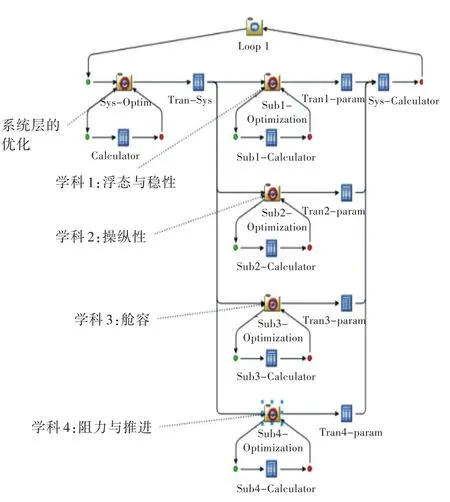
图7 基于ATC方法的船舶概念设计多学科优化框架Fig.7 The structure of ship conceptual design based on ATC
多学科优化具体过程为,系统层负责建造经费的控制优化,并对子系统层提出优化目标;子系统层负责各学科的设计,以及与系统层的协调。
1)系统级优化问题:
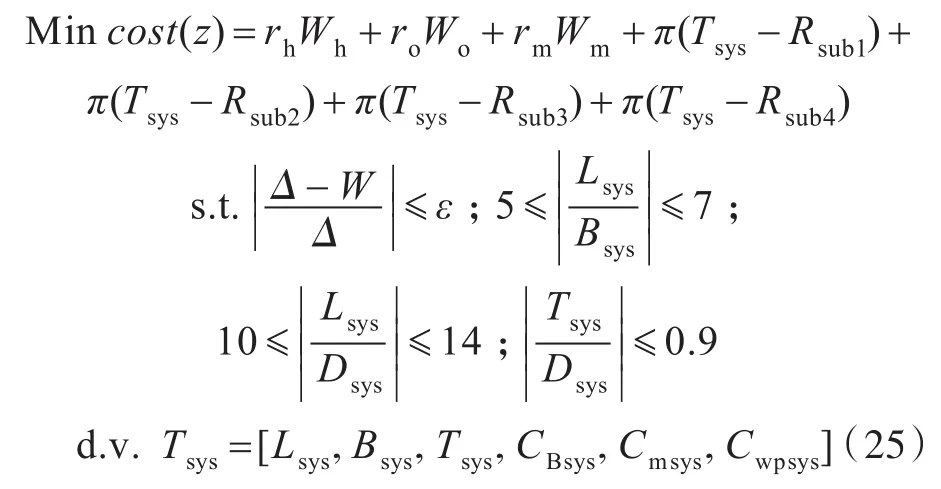
其中,π(T-R)采用增广拉格朗日一致性松弛函数更新,即
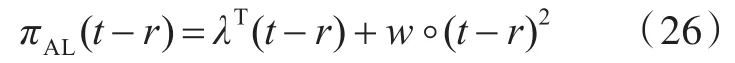
其中,第1个约束表示船舶重量W和排水量Δ相等,考虑初步设计阶段误差,控制二者误差在5%以内,即。
2)子系统3:以阻力与推进子学科优化问题为例,优化数学模型如式(27)所示。
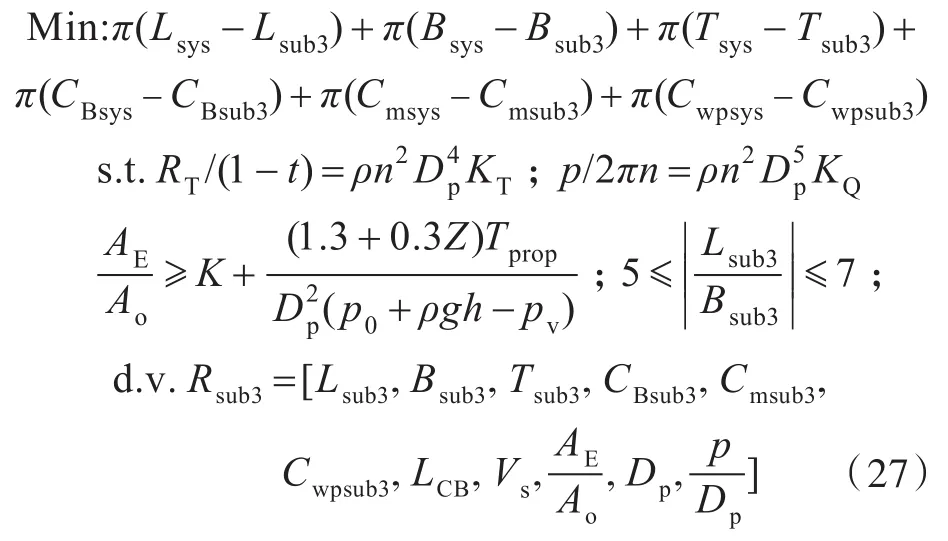
式中:K=0.2,为常数;Z为桨叶数;p0为标准大气压;ρ为空气质量密度;h为桨轴沉没深度;g为重力加速度;pv为气化压力。式(27)中,2个等式约束分别表示桨推力与阻力的平衡、桨转矩与主机输出扭矩的平衡。
3.4 设计优化结果
基于文中给出的船舶概念设计数学模型,在搭建的目标分流优化框架下,通过设定以下优化、约束参数,可开展优化求解:
1)系统与子系统一致性的约束误差不大于1×10-4;
2)增广拉格朗日一致性松弛函数初始值为λ=0,w=1.2;
3)系统层、子系统层均采用常规的二次序列搜索算法。
系统层经过32轮搜索求解,得到了优化方案,优化结果如图8~图11和表2所示。
通过该算例求解分析表明,采用面向目标的分解策略建立船舶概念设计的多层级设计优化结构,并应用ATC优化方法可实现总体与各子系统(单学科)的并行设计与优化。其中,采用增广拉格朗日松弛的ATC方法具有较好的收敛性和稳定性,通过设置合适的初始权重系数和迭代步长,可高效求解得到总体层与系统层相互匹配的优化结果,一致性误差满足工程要求。
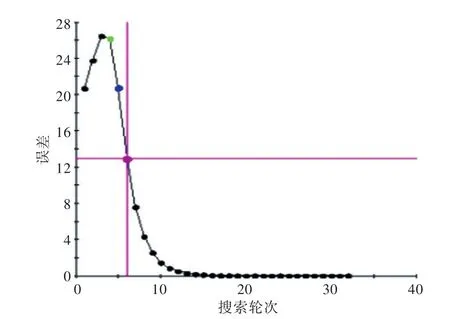
图8 系统层间的一致性误差Fig.8 Plot for convergent error between systems
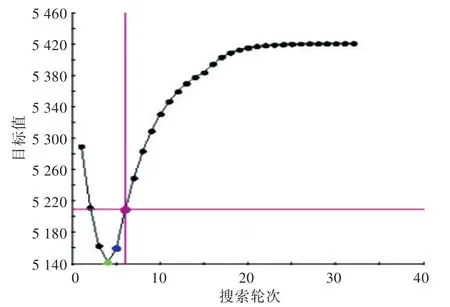
图9 系统层的设计优化目标Fig.9 Plot for objective function
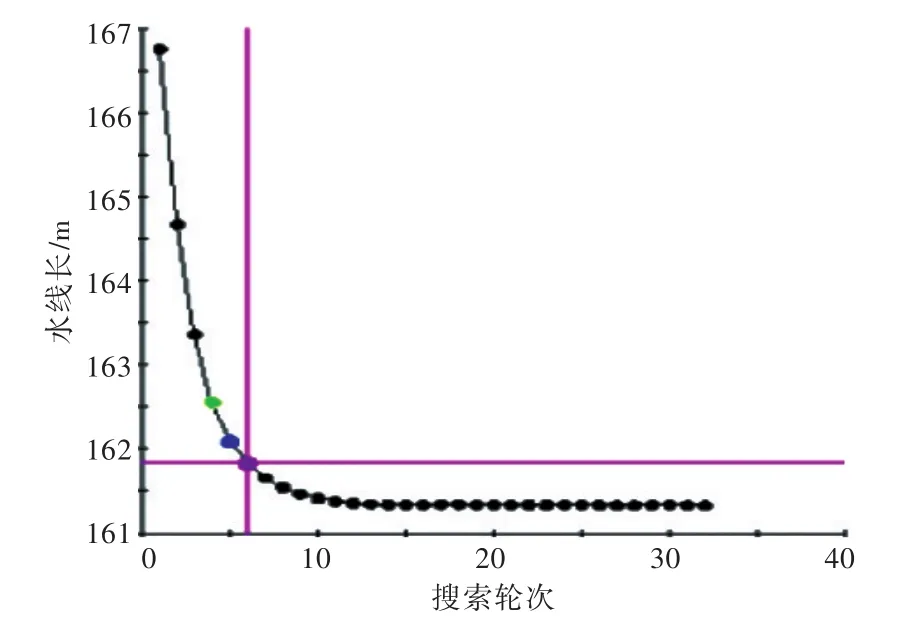
图10 水线长LWL优化过程Fig.10 Plot for LWLin pptimization process
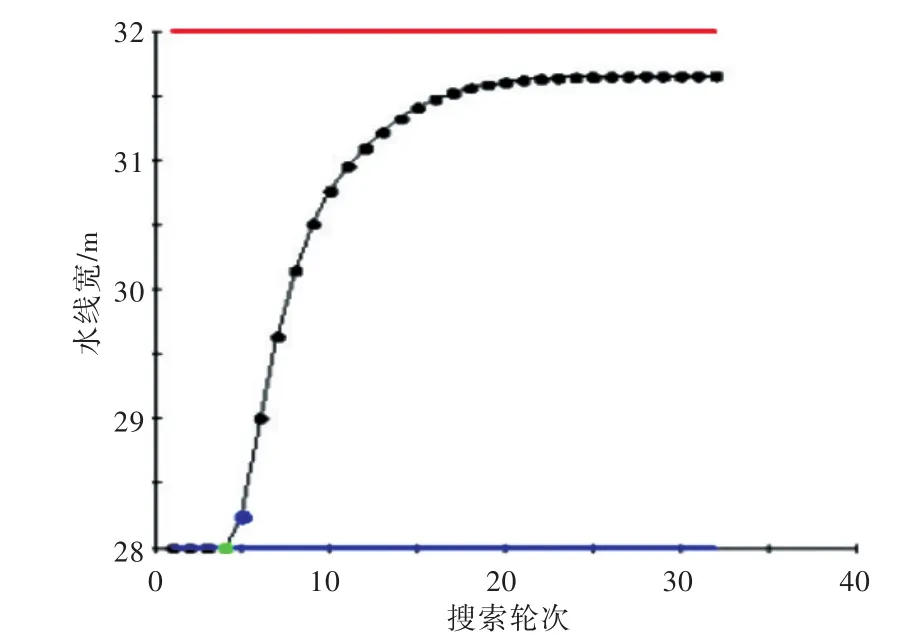
图11 水线宽BWL的优化过程Fig.11 Plot for BWLin optimization process
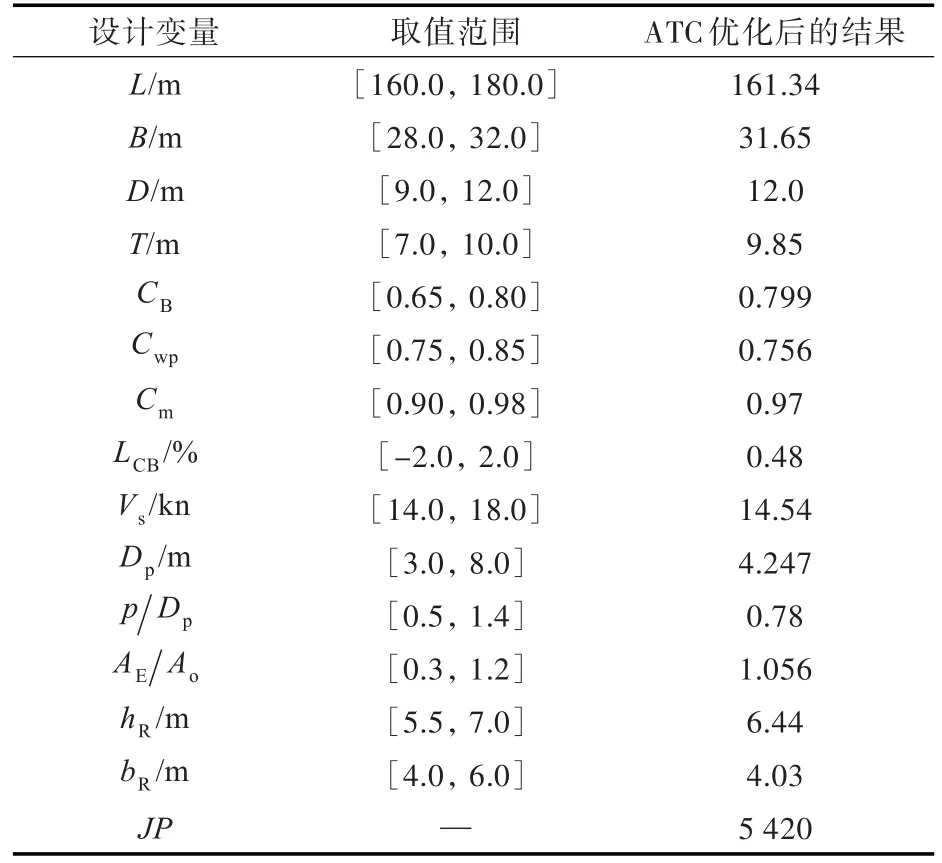
表2 设计变量及目标优化结果Table 2 The optimization results of design variable and objective
4 结 语
本文构建了简化的船舶概念设计数学模型,并应用目标分流方法进行了设计优化,算例结果表明了该多学科优化方法在舰船总体概念设计优化中的合理性与有效性:
1)目标分流法符合系统工程思想,强调从整体出发对各局部的协调,有利于充分发现和利用各子系统的协同效应;
2)目标分流法可促进舰船总体设计的并行,一旦子系统满足设计目标,较低层次的元素就可以在细节上被独立设计。
对于船舶实际工程研制,总体设计接口更为复杂,各子学科分析可以引入数值仿真软件,或利用近似技术,以更高效地获得准确的优化方案。
[1]邵开文,张骏.总体者,集大成也[J].中国舰船研究,2008,3(1):1-4,12.SHAO K W,ZHANG J.Warship design and integration[J].Chinese Journal of Ship Research,2008,3(1):1-4,12(in Chinese).
[2]徐青.舰船总体设计流程分析[J].中国舰船研究,2012,7(5):1-7.XU Q.Analysis of the overall warship design process[J].Chinese Journal of Ship Research,2012,7(5):1-7(in Chinese).
[3]SOBIESZCZANSKI-SOBIESKI J.Optimization by decomposition:a step from hierarchic to non-hierarchic systems:N89-25149[R].Hampton,Virginia:NASA Langley Research Center,1989.
[4]冯佰威,刘祖源,常海超.多学科设计优化技术在船舶初步设计中的应用[J].中国造船,2009,50(4):109-116.FENG B W,LIU Z Y,CHANG H C.Application of multi-disciplinary design optimization techniques in ships'preliminary design[J].Shipbuilding of China,2009,50(4):109-116(in Chinese).
[5]冯佰威,刘祖源,聂剑宁,等.基于iSIGHT的船舶多学科综合优化集成平台的建立[J].武汉理丁大学学报(交通科学与工程版),2009,33(5):897-899.FENG B W,LIU Z Y,NIE J N,et al.Establishment of ship multi-disciplinary design optimization platform based on the iSIGHT[J].Journal of Wuhan University of Technology(Transportation Science&Engineering),2009,33(5):897-899(in Chinese).
[6]KIM H M,MICHELENA N F,PAPALAMBROS P Y,et al.Target cascading in optimal system design[J].Journal of Mechanical Design,2003,125(3):475-480.
[7]KIM H M.Target cascading in optimal system design[D].Michigan:University of Michigan,2001.
[8]LASSITER J B,WIECEK M M,ANDRIGHETTI K R.Lagrangian coordination and analytical target cascading:solving ATC-decomposed problems with Lagrangian duality[J].Optimization and Engineering,2005,6(3):361-381.
[9]KROO I,ALTUS S,BRAUN R,et al.Multidisciplinary optimization methods for aircraft preliminary design[J].AIAA paper,1994,4325.
[10]SOBIESZCZANSKI-SOBIESKI J,AGTE J S,SANDUSKY R R.Bi-level integrated system synthesis(BLISS):NASA/TM-1998-208715[R].Hampton,Virginia:NASA Langley Research Center,1998.
Application of analytical target cascading method in multidisciplinary design optimization of ship conceptual design
WANG Jian1,XIE Wei1,WANG Tao1,LIU Xiaojun2
1 China Ship Development and Design Center,Wuhan 430064,China
2 Special Equipment Safety Supervision Inspection Institute of Jiangsu Province,Zhenjian 212000,China
U662.2
A
10.3969/j.issn.1673-3185.2017.05.003
2017-03-15< class="emphasis_bold">网络出版时间:
时间:2017-9-26 11:08
王健(通信作者),男,1980年生,博士生,工程师。研究方向:舰船总体研究与设计。
E-mail:13797049060@139.com
谢伟,男,1969年生,博士,研究员,博士生导师。研究方向:舰船总体研究与设计
http://kns.cnki.net/kcms/detail/42.1755.TJ.20170926.1108.030.html期刊网址:www.ship-research.com
王健,谢伟,王涛,等.基于目标分流方法的船舶概念方案多学科设计优化[J].中国舰船研究,2017,12(5):22-29.
WANG J,XIE W,WANG T,et al.Application of analytical target cascading method in multidisciplinary design optimization of ship conceptual design[J].Chinese Journal of Ship Research,2017,12(5):22-29.
——“永远跟党走”黄浦江两岸光影秀的总体设计考虑

