基于压缩感知的图片压缩与加密GUI系统①

吕 军, 陈 烁, 李秀梅



基于压缩感知的图片压缩与加密GUI系统①

吕 军, 陈 烁, 李秀梅

(杭州师范大学信息科学与工程学院, 杭州 311121)

利用Matlab平台设计了基于压缩感知的图片压缩和加密GUI系统, 主要解决海量图片的存储空间利用率低和图片数据安全问题. 本系统采用小波变换基将图片系数稀疏化, 将使用高斯随机矩阵进行压缩测量后得到的数据存储在服务器中, 以减少存储空间, 提高服务器空间利用率; 同时将测量矩阵作为密钥进行加密, 增加了图片信息的安全性, 在需要访问时使用密钥矩阵和重构算法重构出原始图片. 该GUI系统能够直观反映基于压缩感知的图片压缩与加密系统的工作过程. 并且通过MCC将代码独立化为可执行exe文件, 以便于直接对图片进行压缩、加密、存取和重构.

压缩感知; 高斯随机矩阵; 正交匹配追踪算法; 图片加密

随着互联网络的快速发展, 各种社交网站和电子商务越来越流行, 海量数据尤其是图片的存储需求越来越大. 然而, 如果把所有图片数据直接存储到服务器, 就需要拥有超级庞大的服务器群来处理、传输、存储图片, 并需要投入大量的资金去维护服务器的正常运行. 并且, 对于一些沉积在服务器中很少被用到的图片数据, 占有存储资源是一种极大的浪费. 现如今, 云存储越来越盛行, 为了防止数据的丢失, 越来越多的移动端用户将自己的图片数据备份到云上, 而数据的安全隐私就没有了保障, 因此对于上传数据图片的加密要求越来越迫切.

为了缓解海量图片存储对于服务器的存储压力, 减少图片存储的空间大小, 我们可以利用压缩感知这一新兴的信号处理理论, 将图片进行压缩测量后存储在服务器上. 压缩感知是2004年提出的信号处理理论, 打破了奈奎斯特采样定理, 实现了采样与压缩的同步完成, 避免了不必要的资源浪费[1,2]. 压缩感知利用空间描述信号, 通过直接采样得到少数的线性观测数据, 而这些数据中包含了信号的全部信息, 通过求解一个优化问题就可以从压缩观测的数据中恢复出原始信号. 本文将图片进行压缩测量, 并将得到的少量数据保存到服务器上, 以减少存储需要的空间. 同时, 由于测量矩阵的随机性, 只有知道测量矩阵才能恢复出原始的图片数据. 因此在上传图片压缩测量数据时, 相当于给图片内容做了加密处理, 使得用户的图片数据更加安全.

本文利用Matlab构建了基于压缩感知的图像压缩与加密GUI系统, 采用小波变换基作为稀疏变换基, 将要存储的图片进行稀疏化, 采用高斯随机矩阵对于稀疏后的系数进行压缩测量, 然后将测量数据和测量矩阵以文件的形式存储在本地, 通过网络发送到服务器中. 当需要图片时, 选择数据和对应的测量矩阵, 通过重构算法重构出原始图像. 最后, 为了便于程序的运行, 通过MCC将matlab的GUI代码编译成可执行文件.

本文的其它部分安排如下: 第1部分简单介绍压缩感知的过程, 第2部分介绍了图片压缩与加密系统GUI的设计实现, 并分析了系统实现的效果, 第3部分给出结论.

1 压缩感知过程

1.1 压缩感知

压缩感知主要包括信号的稀疏表示、测量矩阵的构建和信号的重构, 其优势是实现了采样和压缩的同步进行, 核心是通过这种特殊地采样方式得到的少量的低维信号恢复出原始的高维信号[1,2].

压缩感知是通过测量值恢复出原始信号, 其必须满足的条件之一是必须是稀疏的, 但由于本身通常不是稀疏的, 所以首先做稀疏化处理[3]:

(2)

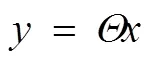
然而, 由来求解的方程式是一个欠定方程, 因此需要求解一个复杂的优化问题:

求解压缩感知问题(4)需要满足两个条件: 信号的稀疏性; 测量矩阵与稀疏基之间的非相干性或者信息算子满足RIP(约束等距性质)[4,5]. 虽然自然信号大多不是稀疏的, 可以通过稀疏基得到原始信号的稀疏系数, 对于稀疏系数做压缩感知的过程, 最后再反变换得到原始信号. 而测量矩阵与稀疏基之间的非相干性意味着它们不能相互稀疏表示. 非相干性越小, 压缩测量需要的测量数量就会越小, 即压缩测量中包含的的信息就越多. 当测量矩阵和稀疏基之间的非相干性达到最大值时, 压缩感知只需个压缩测量就能以很大概率精确重构出原始信号, 其中为原始信号在域上的稀疏度. 而满足RIP性质即约束等距约束常数, 使得任意2列组成的子矩阵趋向于正交, 压缩感知转化为约束范数最小化的凸优化问题, 从而保证压缩感知在数值计算上的可行性, 当的2阶等距约束常数小于, 约束最优化问题(4)能够利用个压缩测量精确重构原始信号[5].

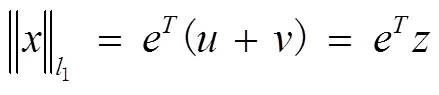
(6)

这是一个经典的线性规划问题[6], 利用一般的求解线性规划工具可以求解出未知变量.

1.2 信号的重构算法OMP

压缩感知的信号重构算法中常用的分为贪婪算法和凸优化算法[7,8]. 本文中采用的是贪婪算法中的OMP算法实现信号的重构[7,8]. OMP算法是由匹配追踪算法MP改进而来, MP的基本思想是在每一次迭代过程中, 从过完备字典原子库(测量矩阵)中选择与信号最匹配的原子来构建稀疏逼近, 且求出信号表示残差, 接着继续选择与信号残差最为匹配的原子. 这样经过一定次数的迭代, 信号可以由一些原子线性表示, 但由于信号在选定原子(测量矩阵的列向量)集合上的投影的非正交性使得每次迭代的结果可能是次最优的, 获得收敛可能需要较多次数的迭代. OMP继承了MP的原子选择原则, 通过递归地对已选原子集合进行正交化以保证迭代的最优性, 减少迭代次数. 其算法步骤如下:

输入:

(2)维的观测向量;

(3) 稀疏度;

输出:

(2) 重构误差;

(1) 循环找到观测矩阵的列向量与冗余向量的内积最大的索引位置;

需要说明的是, 本文采用OMP算法进行图像的重构与加密, 也可以采用其它的信号重构算法, 如CoSaMP算法[9]和稀疏贝叶斯学习[10]等.

2 基于压缩感知的图像压缩与加密GUI系统设计

该部分将在Matlab开发环境下, 完成基于压缩感知的图像压缩与加密GUI系统, 包括界面设计和算法程序设计. 系统框图如图1所示.

利用该GUI可视化系统, 用户只需在主界面选择进行压缩或恢复. 当进行压缩操作时, 可以选择是否使用密钥. 若选择使用密钥, 则选择要处理的图片, 不必选择测量矩阵(后台自动随机产生), 点击压缩按钮, 显示压缩测量后的图片, 并将压缩测量数据和对应的测量矩阵存储到本地文件夹; 若不选择使用密钥, 则选择要处理的图片, 选择一个测量矩阵(测量矩阵为压缩端和恢复端约定共享的固定矩阵), 点击压缩按钮, 显示压缩测量后的图片, 点击另存为将压缩测量数据保存到本地文件夹.

图1 系统框图

当进行恢复操作时, 若压缩时选择不使用密钥, 这里也选择不使用密钥, 进入相应GUI界面, 选择压缩保存的数据后, 进行图片的重构显示, 并将重构的图片保存下来; 若压缩时选择使用密钥, 这里也选择使用密钥, 进入相应GUI界面, 选择保存的数据, 选择保存数据对应的密钥, 进行图片的重构显示, 并将重构的图片保存下来.

需要说明的是, 在没有选择密钥的情况下, 测量矩阵是事先构造好并存储下来的, 压缩端和恢复端共享, 分为五种; 在选择密钥的情况下的测量矩阵是程序运行时随机生成的; 在压缩和恢复操作时对于同一个图片的操作必须要同步, 即加密的情况就必须选择加密, 不加密的情况下必须选择相同种类的测量矩阵.

2.1 压缩与加密GUI系统演示

下面以变换基选择小波变换基、测量矩阵选择高斯随机矩阵、重构算法选择正交匹配追踪算法OMP, 选择加密的方式压缩和恢复图片. 首先, 进入压缩图片的主界面, 进行压缩操作, 如图2所示. 并把压缩后的图片数据和随机产生的测量矩阵保存上传服务器中, 如图3所示.

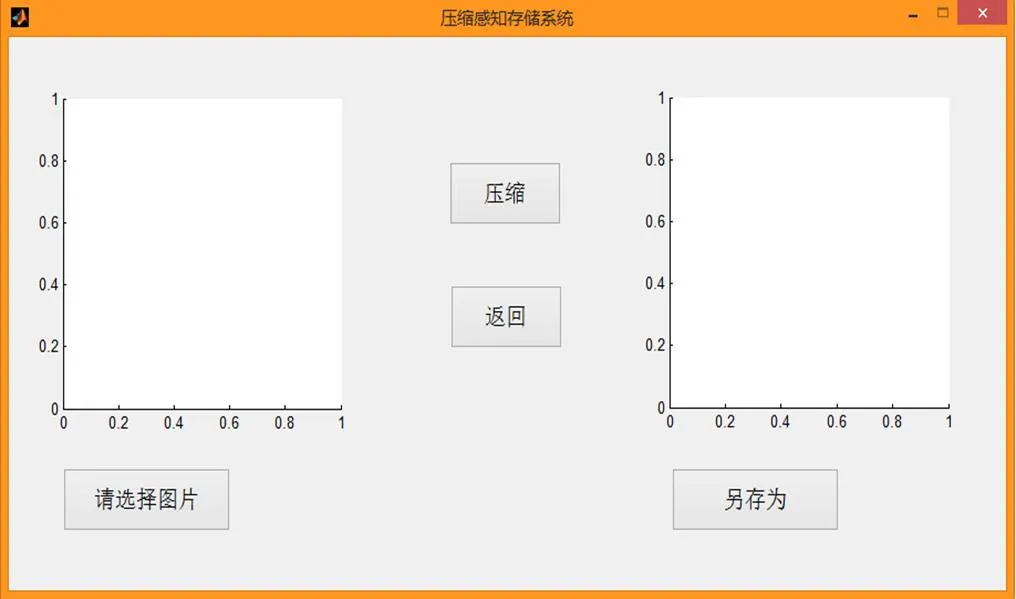
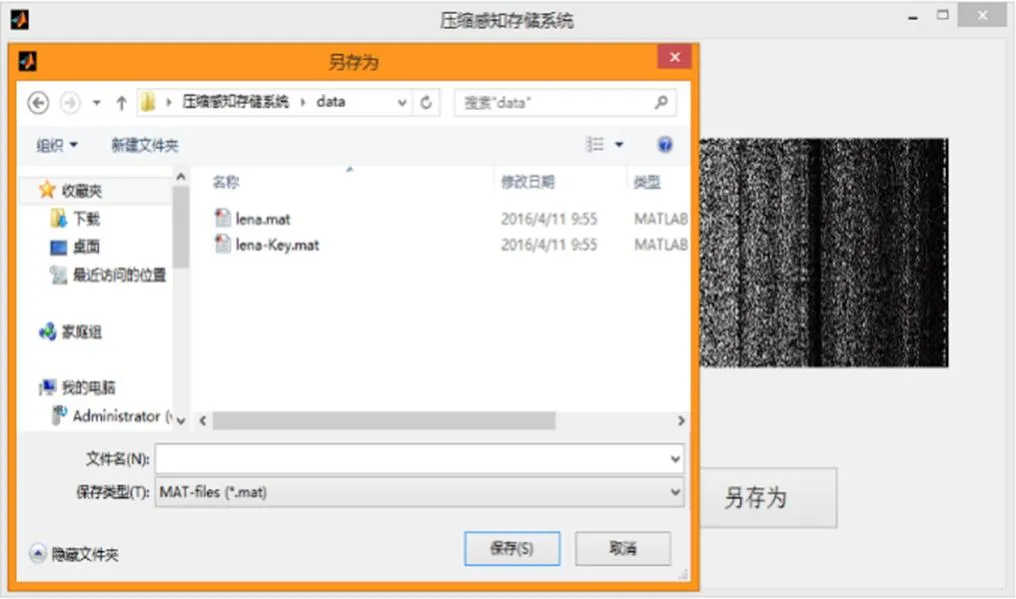
图3 压缩后的图片存储

在用户主界面中, 选择“恢复”按钮, 得到服务器中压缩数据进行恢复操作. 进入图4的GUI界面.

选择对应的密钥, 得到恢复的图像如图5所示, 将恢复的图片显示给用户.

同样, 可以选择不使用密钥的过程, 此时压缩端和恢复端都会出现一个测量矩阵的下拉框, 在两端选择相同的测量矩阵, 即可实现图片的压缩和恢复.

对于灰度标准图中选取的不同的图片进行测试, 结果如表1所示.

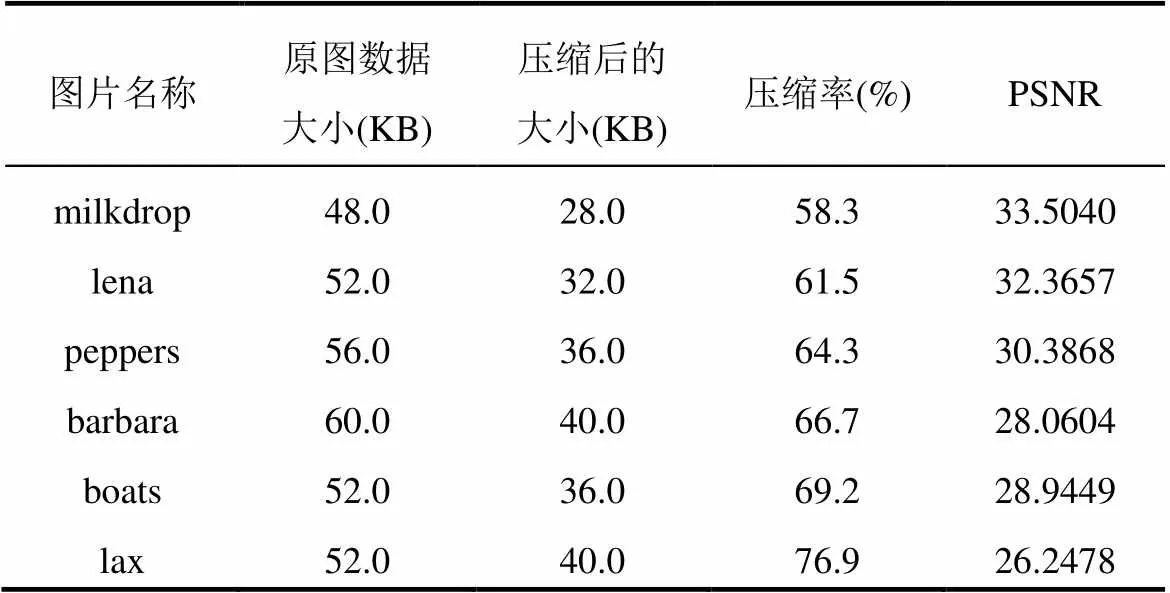
表1 图片压缩前后对比表

其中压缩率=压缩后的空间/原始文件的空间,是评价图像的客观标准,,是每个采样值的比特数,,和分别是原图片和重构后图片的第个像素的灰度值,,表示图像横向和纵向的像素点个数. 由于人眼的视觉对于误差的敏感度并不是绝对的, 其感知结果会受到许多因素的影响而产生变化, 为了便于实验效果的比对, 引入这一最广泛的客观评价标准.值越大表示重构图片与原始图片的差异越小, 重构的图片越接近原始信号.

从表1可以看出, 当压缩率达到60%左右时, 依然可以获得较高的, 即重构图片的质量依然较高.

2.2 利用MCC编译为可执行文件

为了便于程序的运行, 可利用MCC将Matlab代码编译成为可执行文件, 主要步骤如下:

(1) 安装编译器: 可以选择自带的LCC.

(2) 设置编译器: 在Matlab命令行中输入mbuild –setup,选择安装的C语言编译器.

(3) 进入GUI系统所在目录, 命令行输入mcc-m filename, 其中filename是需要转化为exe文件的.m文件.

(4) 安装 oolboxcompilerdeploywin64目录下的MCRInstaller.

通过以上的步骤将Matlab代码生成一个可执行文件, 双击即可运行GUI系统, 方便操作, 无需安装Matlab编辑器.

3 结论

本文利用Matlab设计了基于压缩感知的图像压缩与加密GUI可视化系统, 以解决目前海量图片的存储问题以及图片内容的加密问题. 基于压缩感知信号处理框架, 将图片在服务端的压缩存储和客户端的显示过程进行的直观仿真, 有效提升了服务器端存储空间的利用率, 有效地解决了大数据时代的海量数据的存储问题; 由于压缩测量使用的是随机矩阵, 对于图像信息起到了加密作用, 在没有测量矩阵的情况下很难得到图像的数据信息, 保证了图像的安全性. 最后, 为了方便直接运行, 通过MCC将所有的代码独立化为可执行文件.

1 Donoho D. Compressed sensing. IEEE Trans. on Information Theory, 2006, 52(4): 1289–1306.

2 Baraniuk RG. Compressive sensing. IEEE Signal ProcessingMagazine, 2007, 24(1): 118–121.

3 Ganguli S, Sompolinsky H. Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Annual Review of Neuroscience, 2012, 35(5): 485–508.

4 Candes E. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Mathematique, 2008, 346(9-10): 589–592.

5 邵文泽,韦志辉.压缩感知基本理论:回顾与展望.中国图形图像学报,2012,17(1):1–12.

6 Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. The Annals of Statistics, 2004, 2(32): 407–499.

7 Majumdar A, Krishnan N, Pillai SRB, et al. Extensions to orthogonal matching pursuit for compressed sensing, communications. National Conference on Communications (NCC). 2011. 1–5.

8 方红,杨海蓉.贪婪算法与压缩感知理论.自动化学报,2011, 37(12):1413–1421.

9 Needell D, Tropp JA. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Applied and Computational Harmonic Analysis, 2009, 26: 301–321.

10 Ji S, Xue Y, Carin L. Bayesian compressive sensing. IEEE Trans. on Signal Processing, 2008, 56(6): 2346–2356.

Compressive Sensing Based Image Compression and Encryption GUI System

LV Jun, CHEN Shuo, LI Xiu-Mei

(School of Information Science and Engineering, Hangzhou Normal University, Hangzhou 311121, China)

In this paper, we design an image compression and encryption GUI system based on compressive sensing with Matlab platform, to improve the image storage space utilization and to increase the security of the image data. The system adopts the wavelet transform to decompose the data of images into sparse coefficients, uses Gaussian random matrix to sample the coefficients and stores in the server, to improve server space utilization; meanwhile the system takes the measurement matrix as a key to encryption, increasing security of the image information.The key matrix and reconstruction algorithm are used to reconstruct the original image when needed. The GUI can help to illustrate the process of the image compression and encryption system based on compressive sensing. Additionally, we compile the code into independent executable file, in order to run directly on the image compression, encryption, access and reconstruction.

compressive sensing; Gaussian random matrix; orthogonal matching pursuit algorithm (OMP); image encryption

国家自然科学基金(61571174);浙江省自然科学基金(LY15F010010)

2016-04-23;收到修改稿时间:2016-05-30

[10.15888/j.cnki.csa.005555]