单线图动态规划最优布局成图技术①

赵 越, 李 培, 王 震, 王 平



单线图动态规划最优布局成图技术①

赵 越1, 李 培1, 王 震2, 王 平2

1(国网江苏省电力公司扬州供电公司, 扬州225000)2(厦门亿力吉奥信息科技有限公司, 厦门361008)

提出了一种基于动态规划算法得到布局最优解实现区域电网单线图生成的方法. 根据电网空间数据构建拓扑模型, 执行广度优先算法得到多个能构成连通图的邻接矩阵以及矩阵遍历序列, 根据邻接矩阵宽度计算出能容纳全部设备的正方形范围, 并建立了设备最小间距为优化目标的数学模型. 提出了动态规划最优布局求解的算法, 应用该算法求解布局最优解数组, 最后按照最少交叉原则进行正交化处理. 应用实例表明通过最优解布局的成图美观且高效.

区域电网; 拓扑模型; 动态规划算法; 单线图; 布局最优解

单线图对于电网的意义和价值非常大, 不管是配网生产的规划设计、电网调度的调度管理还是配网运行的运行检修, 单线图都是一种必不可少的常用工具. 不过随着电网建设更新日新月异, 单线图更新也日益频繁, 同时电网用户对于单线图的展现效果要求亦不断提高, 因此单线图的维护工作量越来越多, 如果能有一种可行、高效、美观的单线图自动生成方法来解决这个难题, 就可以进一步提高配网生产的工作效率.

当前国内许多学者针对电网地理信息到单线图的自动生成课题进行了大量研究[1-3]. 同时国内外还有很多学者对于退火算法、树图算法、遗传算法等各种先进算法在单线图布线上的结合应用也进行了研究和实践[4-13]. 以上文献提出的单线图自动生成方法都有一定的参考价值, 但是无法满足目前日益复杂的电网结构以及用户不断提高的布局展示要求.

如何设计合适算法, 结合电力GIS系统准确高效的实现单线图的自动生成, 值得进行深入研究, 本文在深入了解电网单线图自动生成具体要求以及综合各种先进布局理论算法后, 提出了运用动态规划算法分阶段计算并最终得到符合电网生产实际使用所需单线图自动生成的方法.

1 基于动态规划算法的图形布局机制

目前行业内存在各种专题图系统, 其中图形布局所采用的算法基本上为以下三种算法.

a) 树图布局算法: 层次数据的空间填充性布局算法;

缺点: 应对复杂层次数据时, 有序树图正方化性能差, 难以满足各层数据展现需求, 需要人工参与.

b) 正交遗传算法: 通过旋转正交法快速提取解空间中的优异个体的布局算法;

缺点: 算法对新空间的探索能力是有限的, 也容易收敛到局部最优解. 涉及到大量个体的计算, 当问题复杂时, 严重影响性能, 同时对非线性约束的处理方式是添加惩罚因子, 这是一笔不小的性能开支.

c) 有向无环算法: 采用消环、分层、排序、路径管理的布局算法.

缺点: 很多电网数据局部成环, 无法处理.

为了避免布局时的人工参与, 减少计算性能消耗, 在通过综合蚁群算法、褪火算法、正交遗传算法、贪心算法、动态规划算法等先进理论算法后, 最终在动态规划算法的基础上延伸拓展出最适合电力网络的布局算法.

动态规划算法基本思想与分治法类似, 将问题分解为N个子问题, 依次解决各子问题, 最后一个子问题就是初始问题的解. 在实际应用中动态规划算法可按以下几个简化的步骤进行设计:

(1) 分析最优解的性质, 并刻画其结构特征;

(2) 递归的定义最优解;

(3) 以自底向上或自顶向下的记忆化方式(备忘录法)计算出最优值;

(4) 根据计算最优值时得到的信息, 构造问题的最优解.

2 单线图自动生成技术设计思路

基于动态规划最优布局算法的单线图自动生成设计思路如下.

a) 根据源地理沿布数据建立电网拓扑存储模型, 实现设备、单线图、拓扑关系的存储, 然后完成各段拓扑模型的去重、合并处理, 建立网络图拓扑模型;

b) 根据网络图拓扑模型, 建立连通图得到连通图的邻接矩阵, 然后采用广度优先遍历算法遍历邻接矩阵顶点得到矩阵遍历序列;

c) 开启动态规划算法对序列中的顶点信息求解最优值, 得到最优值数组[];

d) 遍历最优值数组, 按照最优值坐标放置设备, 通过图形引擎完成每一个设备的渲染绘制;

e) 以最少交叉原则完成图纸正交化处理.

上述步骤中, 重点在a步、c步、e 步中, 即如何建立网络图的拓扑模型和计算网络图设备最优坐标. 本文的处理方法是采用动态规划的方法结合电力接线图特点计算得到设备布局最优值数组.

3 网络图拓扑模型构建

(1) 单线图对象存储

根据电力系统的空间数据, 按照线路进行分类存储设备信息和拓扑关系, 即构建多线路模型, 以单条线路为标记, 分别存储各自对应的设备信息和拓扑关系.

//单线图对象

{

;// 设备集合

; //版本信息

;// 图档类型

;// 变电站名称

; //馈线

;// 馈线名称

;// 坐标原点

; //连接关系列表

;// 关联关系(包含关系)

}

(2) 网络图对象存储

构建基于单线图的环网拓扑关系模型, 用于确定子图档与子图档之间的关系, 构建连通图模型, 通过联络关系来确定线路之间的关系是否正常, 联络关系为环网点(环网开关), 拓扑关系模型包括馈线F1、馈线F2和联络开关K三个基本属性.

//网络图对象

{

;// 版本信息

>;// 包含的子图档

;// 联络关系

}

//联络关系模型

{

;// 联络开关

1;// 馈线1的;

2;// 馈线2的

;// 与联络开关相连的设备

}

(3) 合并与去重复处理

对构建的各段拓扑关系模型进行合并和去重处理; 其中, 如有需要还可以简化设备, 形成新的拓扑关系模型. 如图 1、图2 所示, 2 段拓扑中 A1 与A2(B1 与 B2)均代表同一个设备, 为消去相同的, 需要对两段拓扑中的A、 B 两个设备进行去重与合并处理, 融合成 A12、B12, 结果如图 3 所示.

图1 拓扑段1

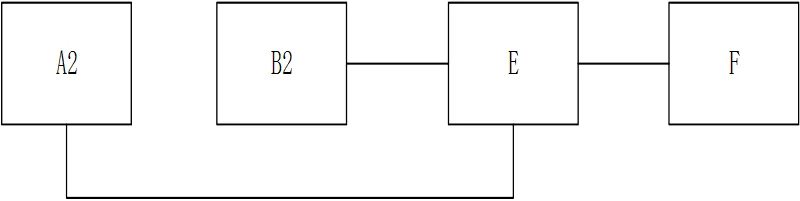
图2 拓扑段2

图3 拓扑段合并处理结果

最初的线路模型经过去重与合并处理后生成了单条或者多条大的网络拓扑模型.

4 基于动态规划的成图布局处理

4.1 基于动态规划的最优值求解

(1) 获取容纳全部设备的正方形范围

根据邻接矩阵的宽度, 计算出一个能容纳全部子图档并留有最少空位的正方形范围, 考虑到范围越大, 计算函数需要花费的时间越大, 所以使用一个能容纳全部子图档并留有最少空位的正方形范围;

满足:>=(-1)*(-1);

(2) 建立设备最小间距的目标函数模型

遍历第一个设备到最后一个设备, 如果两个设备间有连接关系(,), 就计算两个点之间的距离, 不重复计算距离, 为了减少设备间连接的交叉, 构建的函数模型应满足有关系设备尽量紧凑, 同时不能重叠.

对应的函数模型为:

为计算设备间距离的公式:

其中,和属于1到L之间的正整数, 代表每个备中心点的坐标值;

(3) 动态规划算法求解最优值

开启动态规划算法, 迭代寻找函数新的最优解, 直到确定每个设备中心点的x和y的值.

a) 根据Link的长度(序列长度=设备数量)计算出顶点范围, 构建*个格子, 每个格子用于存储当前格子存储的设备下标编号和对应的,值;

b) 根据动态规划算法, 按下标计算出第一个设备顺序放入空闲格子的函数值;

c) 根据连接关系寻找最优解并迭代执行该过程, 直至设备全部遍历完成, 在迭代过程中需要判断设备是否有连接, 如果无连接, 则将下标记录到无连接数组中, 继续迭代该过程; 否则进行动态规划算法, 按下标继续放置设备;

d) 遍历完序列Link后, 整理数据, 遍历每个子图档存储的唯一格子对象, 根据格子对象中的设备对象的下标进行排序, 并返回每个设备的和值.

本算法中, 以计算解出的值是否为最小值为最优解, 即如果为最小值则记录为最佳位置, 直至计算完毕后无法找到更小值为止. 计算完毕后, 如图4所示, 按下标存储每个设备的最优解, 最优解数组的格式为[](二维整形数组), 比如[1,1], [2,2], [3,3]..., [1,1]对应设备1的最佳位置.

得到最优解数组的动态规划最优布局算法如图4所示.

图4 最优解数组生成流程图

4.2 基于动态规划的图纸正交化处理

经过之前的处理, 每个设备都已经按层等间距互不重叠地排列, 后续的调整都不应该再调整设备的坐标, 所以我们参考设备的位置来完成图纸正交化处理

根据单线图基本布局规则, 所有设备之间的连线都应该是横平竖直的, 所以需要对设备连接线按照某些规则添加一些拐点形成正交化的形态. 我们目前采用的是动态规划的方法为边线添加拐点达到正交化, 图5是一幅最优布局后的图, 我们从上到下逐层调整上下子设备之间的边线.

以上图为例调整上游设备与各下游设备之间连线的正交化. 首先求得上游设备连线的数目,然后求出一个中位数/2

对于每一条连线做如下处理:

(=-1;>=0;--)

{

处理左边正交化;

+=3.0;;

}

(=;j<;++)

{

(==)

{处理中间正交化;MiddleSpace+=2.0;}

Else

{处理右边正交化;RightSpace-=3.0;}

}

a) 处理左连线正交化

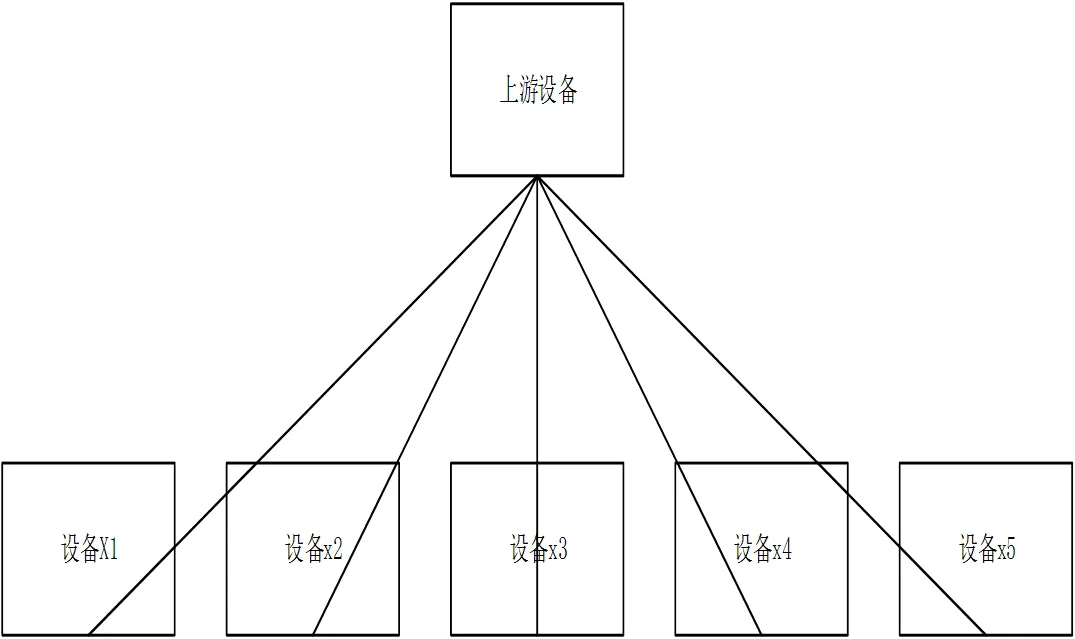
图5 设备连线正交化处理前

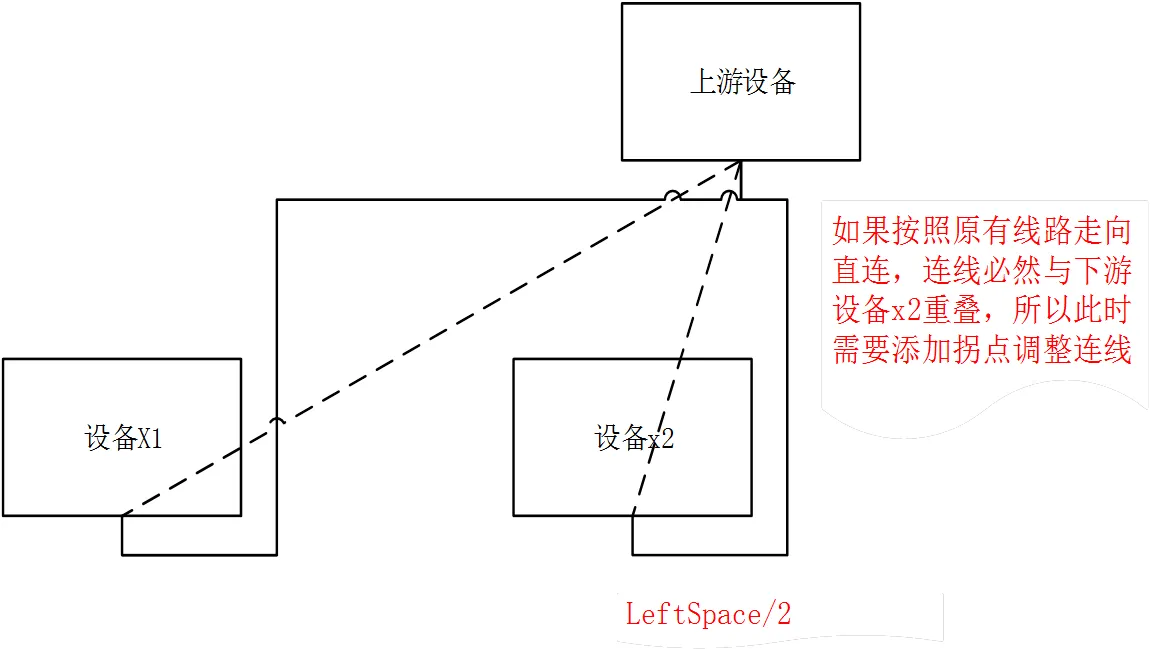
图6 处理左连线正交化

b) 处理中间连线正交化

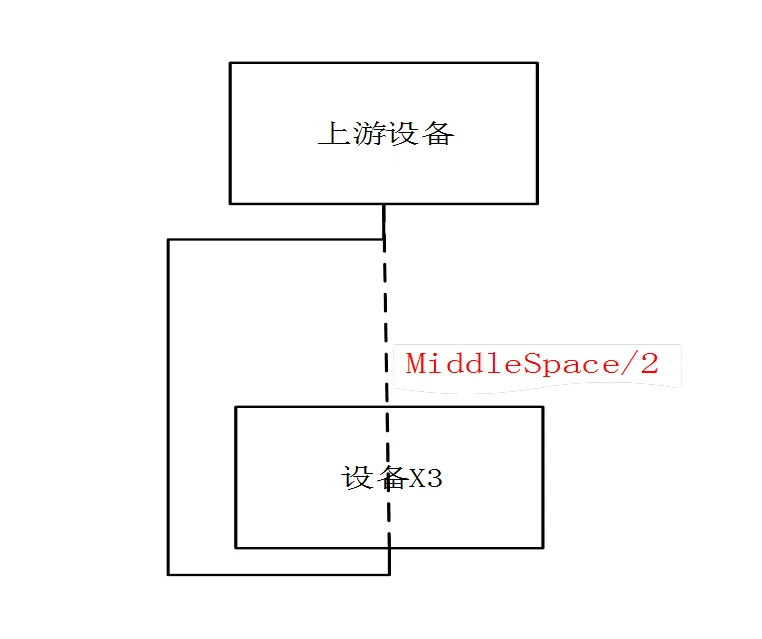
图7 中间连线正交化

c) 处理右连线正交化

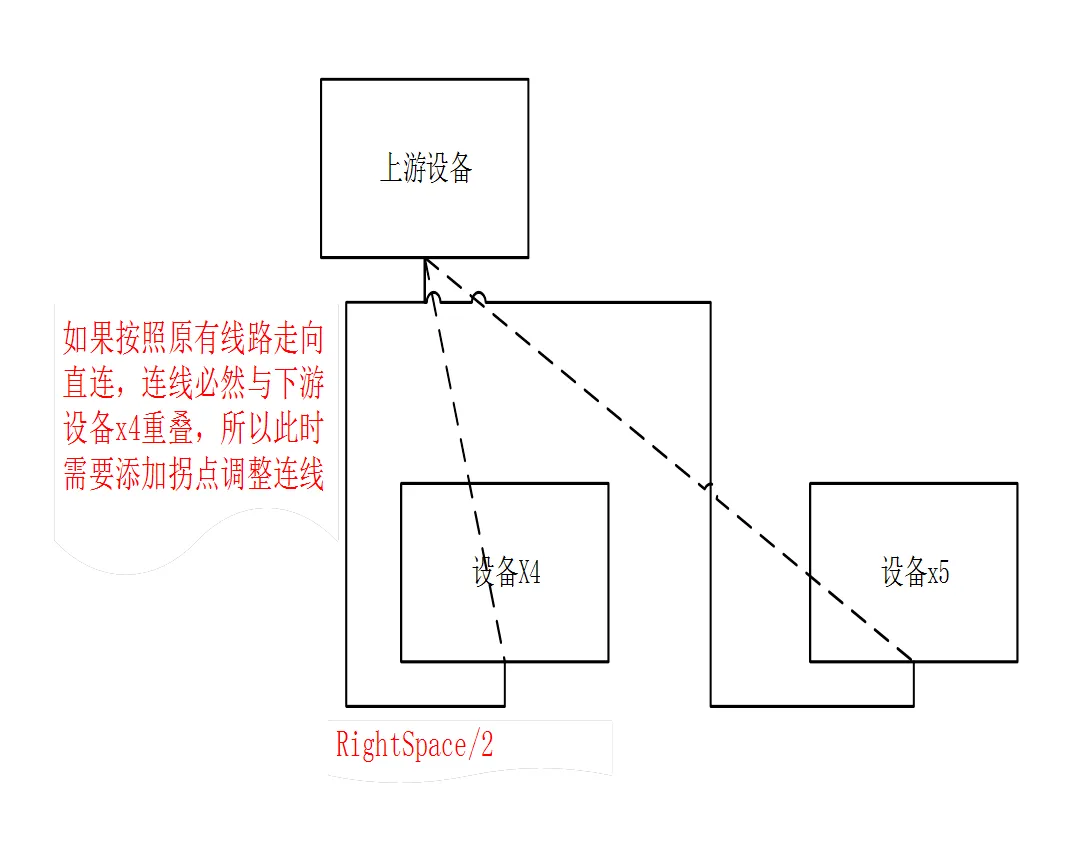
图8 右连线正交化

以上三种处理方法都要考虑到一种情况, 如图9, 设备X2 本身有多条线穿出, 当前调整的这条线从哪边穿出能减少与其他边的交叉是很值得考虑的.

图9 连线正交化参考下游设备调整

5 算法示例

本文引用某地区电网架构模型, 该模型具备线路之间环网多的特点, 可用于验证上述原理. 某地区局部电网联络线路数据如表1所示.

表1 某地区局部电网联络线路数据

表中, 第1列表示联络开关, 第2、3、4、5列都是有联络关系的线路. 某地区电网采用最优布局算法前、后布局如图9, 图10所示. 可以看出采用动态规划最优布局算法布局后图形绘制区域整体布局更加均匀、美观、清晰, 满足单线图自动布局的要求. 验证了基于动态规划方法的最优布局算法的正确性及有效性.

图9 普通算法布局

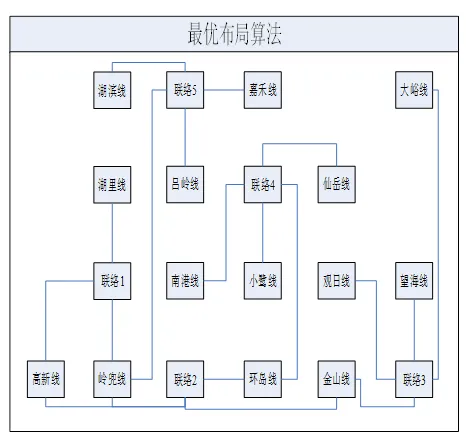
图10 动态规划算法布局

6 结语

本文提出了一种基于动态规划最优布局算法的单线图自动生成方法. 通过分析现有布局算法的不足, 并深入研究布局过程, 采用动态规划思想重新设计布局算法, 为单线图生成的自动布局处理提供了更多的选择. 通过对布局算法的优化, 拓广了动态规划方法的应用范围, 同时提高了单线图自动布局的效率和美观程度.

与现有技术相比, 存在下面两点优点:

第一、提出了由多条线路构成的网络连通图构想方案, 通过函数模型计算出连通图顶点的位置来确定设备的位置, 并且该位置是最合适的, 能够快速、完美成图.

第二、放弃树图布局算法、遗传算法等算法, 通过算法优化, 使用动态规划算法计算出最优解, 而不是近似的最优解.

1 徐彭亮,何光宇,梅生伟,张王俊,王伟.基于地理信息的输电网单线图自动生成新算法.电网技术,2008,32(21):9–12.

2 刘健,吴媛,刘巩权.配电馈线地理图到电气接线图的转换.电力系统自动化,2005,29(14):73–77.

3 章坚民,叶琳,孙维真.基于地理相对位置的省级输电网均匀接线图自动生成.电力系统自动化,2010,(24):55–59.

4 陈学松,蔡述庭.基于模拟退火算法的矩形优化排样问题的研究.数学的实践与认识,2008,38(9):68–71.

5 沈伟,吴文传,张伯明,镐俊杰.能量管理系统中电网潮流单线图自动生成算法.电力系统目动化,2010,34(6):48–53.

6 邢佳磊,杨洪耕,何亚平.地区电网运行单线图的智能自动布局.电力系统自动化,2010,34(4):59–64.

7 王治华,董树锋,张王俊.输电网单线图自生成的新方法.电力系统保护与控制,2010,38(18):155–159.

8 张旭,冯恩民.具有性能约束布局问题的优化算法及收敛性.大连理工大学学报,2005,45(5):766–771.

9 陈勇,邓其军,周洪.无重叠交叉的配电网单线图自动生成算法.电力自动化设备,2010,30(11):90–93.

10 Rossouw FJ, Beukes HJ, Enslin JHR. Modelling network problems with power flow equations and diagrams. AJ. Africon, 1999 IEEE, 1999, (2): 643–648.

11 Deng QJ, Zhou H, Chen Y. Design and implement of drawing of GOO one-line diagram of smart distribution network. 2010 International Conference Electrical and Control Engineering (ICECE). 2010. 3533–3536.

12 Li X, Feng XL, Zeng ZY, et al. Distribution feeder one-line diagrams automatic generation from geographic diagrams based on GIS. Third International Conference Electric Utility Deregulation and Restructuring and Power Technologies (DRPT 2008). 2008. 2228–2232.

13 Zhang LH, Pei XD, Kleine U. Analog macro-cell placement with very fast simulated re-annealing algorithm. Journal of Software, 2002, 13(6): 1059– 1062.

Optimal Layout Mapping Technology for Single Line Dynamic Programming

ZHAO Yue1, LI Pei1, WANG Zhen2, WANG Ping2

1(State Grid Yangzhou Power Supply Company, Yangzhou 225000, China)2(Xiamen Great Power GEO Information Technology Co. Ltd., Xiamen 361008, China)

A new method for generating the single line diagram of the regional power network is proposed based on the dynamic programming algorithm. According to the topological model of spatial data in power grid, the implementation of the breadth first algorithm can obtain the adjacency matrix and matrix traversal sequence of the connected graph, and the square range of the total equipment can be accommodated by the adjacency matrix. A dynamic programming optimal layout algorithm is proposed, which is used to solve the layout optimization problem. The application example shows that the optimal solution layout is beautiful and efficient.

regional power network; topological model; dynamic programming algorithm; single line graph; layout optimal solution

2015-11-13;

2015-12-21

[10.15888/j.cnki.csa.005256]