优先聚类和高斯混合模型树相融合的递增聚类研究

资和周

摘 要： 传统聚类算法实现大数据集聚类时，耗费大量的时间和内存，无法适应大数据流的动态性，聚类稳定性较差。因此，提出基于优先聚类和高斯混合模型树的递增聚类方法。采用优先聚类算法对大数据集进行优先聚类，获取典型数据集，降低大数据集的数据复杂度，采用高斯混合模型树的递增聚类算法，将典型数据集中的数据插入到高斯混合模型树内，塑造数据集的高斯混合模型树，树的叶子节点和非叶子节点分别同单高斯数据分布和高斯混合模型分布对应，基于插入结果对高斯混合模型树实施调整，检测插入到模型树内的数据是否需要删除，并完成数据的删除操作，采用广度优先方法获取最佳的树节点作为最终的聚类结果。实验结果表明该算法取得了很好的效果，具有较高的可扩展性和稳定性。

关键词： 大数据； 聚类分析； 高斯混合模型； 仿真实验

中图分类号： TN911.1?34； TP391.4 文献标识码： A 文章编号： 1004?373X（2017）19?0177?05

Research on incremental clustering integrating priority clustering

with Gaussian mixture model tree

ZI Hezhou

（School of Finance and Trade Management， Yunnan College of Business Management， Kunming 650106， China）

Abstract： The traditional clustering algorithms consume a large amount of time and memory for large dataset clustering， can′t adapt to the dynamic performance of big data flow， and have poor clustering stability. Therefore， an incremental clustering method based on partial?priority clustering and Gaussian mixture model tree is put forward. The partial?priority clustering algorithm is used to perform the priority clustering for large dataset， acquire the typical dataset， and reduce the data complexity of large dataset. And then the incremental clustering algorithm based on Gaussian mixture model tree is used to insert the data in typical dataset into a Gaussian mixture model tree to construct the Gaussian mixture model tree of the dataset. The leaf nodes and none?leaf nodes of the tree are matched with single Gaussian data distribution and Gaussian mixture model distribution respectively. According the insertion results， the Gaussian mixture model tree is adjusted， the data inserted into the model should be deleted whether or not is detected， and data deletion is accomplished. The breadth?first method is adopted to get the best tree node as the final clustering result. The experimental results indicate that the proposed incremental clustering algorithm has perfect clustering effect， strong expansibility， and high stability.

Keywords： big data； clustering analysis； Gaussian mixture model； simulation experiment

0 引 言

隨着计算机和数据分析计算的高速发展，信息在人们的生产和生活中具有重要的作用，并且当前互联网中数据量呈现爆炸式增长，人们需要通过聚类技术从大数据环境中采集有价值的信息。聚类技术在生物学、数据挖掘、信息检索等领域具有较高的应用价值。大数据环境下的聚类技术，成为相关人员分析的重点[1]。当前大数据集的聚类算法主要是静态聚类算法，其对总体数据集进行检索，耗费大量的时间和内存，并且无法适应大数据流的动态性，聚类稳定性较差[2]。因此，本文提出基于优先聚类和高斯混合模型树的递增聚类方法。

1 基于优先聚类和高斯混合模型树的递增聚类

方法

1.1 优先聚类算法

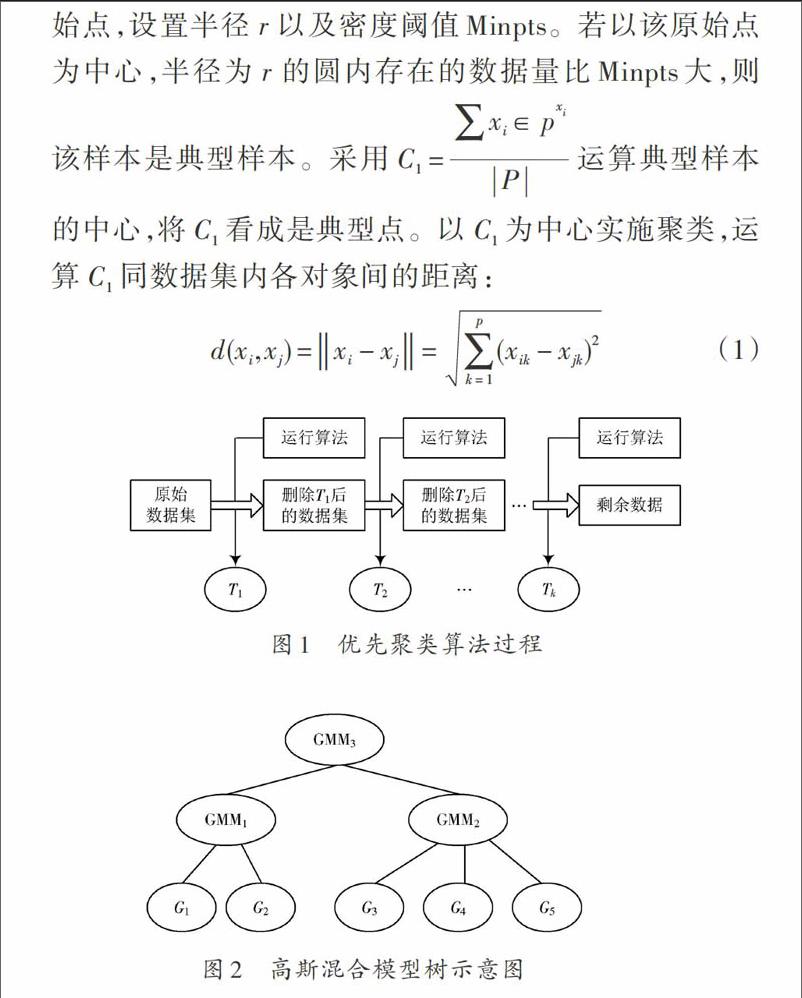
优先聚类算法的示意图如图1所示。

优先聚类算法从某个大数据集内任意采集样本[A，]若分析[A]是典型样本，则获取典型点，否则继续进行分析，直至获取典型样本。随机从[A]内采集一个点当成原始点，设置半径[r]以及密度阈值Minpts。若以该原始点为中心，半径为[r]的圆内存在的数据量比Minpts大，则该样本是典型样本。采用[C1=xi∈pxiP]运算典型样本的中心，将[C1]看成是典型点。以[C1]为中心实施聚类，运算[C1]同数据集内各对象间的距离：

[d（xi，xj）=xi-xj=k=1p（xik-xjk）2] （1）

若[C1]同某对象[xi]间的聚类比数值[r]低，则将该对象划分到该类内，否则分析后续对象，直至完成数据集内全部数据的分析。

设置原始空集是[T1，]并向其融入典型点[C1，]若运算[T1]内全部点同[C1]间的距离比阈值[r]低，则将该对象[xi]融入[T1，]最终获取第一个类[T1。]将该类中的数据从原始数据集内过滤掉，确保[T1]中的数据不再进行后续的分类，降低数据的复杂度。循环进行形成第一类的过程，直到剩余數据不再符合规范，形成相关的类是[T1，T2，…，Tk]。这些类中存在着大部分数据，并且各类中存在一个典型点[Ck（k=1，2，…，k）]。因为剩余数据是不符合规范的点，则将这些数据平均划分成[k]类，再将其分配到前期产生的[k]个[T1，T2，…，Tk]类内，获取的典型数据集是[T′1，T′2，…，T′k （i=1，2，…，k）]。

上述分析的优先聚类算法采用随机大数据集样本，获取典型样本以及典型点，将典型样本的均值当成典型点实现聚类，可提高“召集”数据量，确保原数据集最大程度的缩小。获取首个类后，从原始数据集中将其过滤掉，可大大降低原始数据集的复杂度。

1.2 高斯混合模型树的递增聚类算法

采用1.1节分析的优先聚类算法对大数据集进行优先聚类，获取典型数据集，大大降低了大数据集的数据复杂度，为后续的数据递增聚类过程提供可靠的基础。进而采用高斯混合模型树的递增聚类算法实现大数据集的高精度聚类。该算法将优先聚类算法获取的典型数据集中的数据插入到当前的高斯混合模型树中，基于插入结果对高斯混合模型树实施调整，检测插入到模型树内的数据是否需要删除，并完成数据的删除操作，获取最终的聚类结果。

1.2.1 高斯混合模型树的构建

结合高斯混合模型与树型的框架构成高斯混合模型树。数据聚类、子聚类以及整个数据集间的联系可通过高斯混合模型树呈现。由下至上组建高斯混合模型树的方法与递增聚类的流程一致。叶子节点与单一高斯成分相对应，构成了高斯混合模型树中数据散布程度最密集的区域，高位节点处于数据散布稀疏区域，全部数据集的高斯混合模型分散度与根节点的分散度一致，构成高斯混合模型树中数据分散度最高的区域。数据集中的各聚类簇头同一个高斯混合模型对应，高斯混合模型描述了数据的分散状态[3]。多个高斯混合模型构成了高斯混合模型树。塑造高斯混合模型树的流程与数据集匹配高斯混合模型的流程相同，叶子节点处于数据最密集的区域，树的层数与数据分散度成反比。

高斯混合模型树示意图如图2所示，其中[G1～G3]表示叶子节点，分别与单一高斯成分相对应，GMM1～ GMM3表示非叶子节点，与高斯混合模型相对应。由图2可知，GMM1作为[G1，G2]的父亲节点，其数据分散状态受[G1，G2]的数据分散状态制约。非叶子节点连接着单一高斯成分与高斯混合模型，即非叶子节点的构成可以是单一高斯成分也可以是高斯混合模型。高斯模型GMM1与GMM2组成根节点GMM3。

1.2.2 数据插入

数据插入是塑造数据集的高斯混合模型树的关键。将优先聚类算法获取的典型数据集中的各个新数据点插入到高斯混合模型树的叶子层，获取高斯混合模型树。这个新数据既可能形成新的叶子节点，也可能被安插到已有的叶子节点中。基于对上文的分析，叶子节点反映出高斯混合模型树中单高斯分布最密集的区域，使获取的新数据能够被精确地安插到适合的叶子节点上，需要求出新数据点与全部单高斯成分的平均值的欧式距离，其中与欧式距离最小值对应的则是待检索的叶子节点。阈值[Tinsert]的使用可保障叶子层单高斯成分的密集度[4]，当最小的欧式距离大于该阈值时，会有新的叶子节点诞生，与该叶子节点相应的单高斯成分的方差是一个较小的起始值，数据点即是平均值；当最小的欧式距离小于该阈值时，与最小欧式距离相应的叶子节点会接收新的数据点。如果叶子节点密集度变大，会降低新插入的节点与全部叶子节点欧式距离的运算速度，因此，可由高到低即从根节点开始，依据类条件概率密度的方法确定相似度最高的叶子节点。详细过程为：

（1） 先获取新数据，再对不同的高斯混合模型树已有的叶子节点量采用不同的数据安插方式，比较已存在的高斯混合模型树叶子节点量与设定的阈值，如果已存在的高斯混合模型树叶子节点量不大于阈值，那么接受过程（2）的方式；如果已存在的高斯混合模型树叶子节点量大于阈值时，那么接受过程（3）的方式。

（2） 求出过程（1）获取的新数据与全部单高斯成分的平均值的欧氏距离，并将其中最小的欧氏距离以及与之相应的叶子节点做好标记[5]；当最小的欧氏距离小于等于设定的阈值时，此欧氏距离值由相应的叶子节点保管；当最小的欧氏距离大于设定的阈值时，此欧氏距离值由形成的新叶子节点保管。

（3） 以根节点作为开端，基于类条件概率密度的方法确定相似度最高的叶子节点，类条件概率密度的公式为：

[Co=argmaxkPXCk] （2）

用[k]描述目前数据集相应的聚类量，用[P，X]分别描述条件概率以及数据，用[Ck，][Co]分别描述第[k]个聚类以及符合公式的类。过程（2）中新数据安插到已有的叶子节点时，要对新叶子节点中高斯成分的参数进行更改，更改平均值以及方差的公式为：

[μn+1=μn+1n+1xn+1-μn] （3）

[σn+1=n-1nσn+1n+1xn+1-μnxn+1-μnT] （4）

1.2.3 数据删除

本文研究的递增聚类算法对当前高斯混合模型树中的数据点可以进行删除操作。对数据进行删除与插入数据都是以叶子层节点作为开端。当该叶子节点上仅存在一个数据点时，删除这个数据点也就意味着删除该叶子节点[6]。当该叶子节点上存在多个数据点时，可采用以下公式对叶子节点相应的高斯成分参数进行更改：

[μn+1=nn-1μn-1m-1xn] （5）

[Σn+1=n-1n-2Σn-n-1n?（n-2）xn-μn+1xn-μn+1T] （6）

对式（3）～式（6）的推算过程如下：

针对数据集[D1=x1，…，xm-1，xm，]平均值、方差为：

[μm=1mj=1mxj] （7）

[Σm=1m-1j=1mxj-μmxj-μmT] （8）

新数据点被安插至原数据集，进而得到新的数据集：

[D2=x1，…，xm-1，xm，xm+1] （9）

新的高斯成分的平均值为：

[μm+1=1m+1j=1m+1xj=1m+1j=1m+1xj+1m+1xm+1=mm+11mj=1mxj+1m+1xm+1=mm+1μm+1m+1xm+1] （10）

进而得到高斯成分的新方差，被安插的新数据点相应的平均值以及方差为：

[μm+1=mm+1（xj-m）+m+1m+1μm] （11）

[Σm+1=m-1mΣm+1m+1xm+1-μmxm+1-μmT] （12）

对一个数据点进行删除操作后的数据集为：[D3=x1，x2，…，xm-1] （13）

更改后的平均值以及方差为：

[μm-1=m-xm-1j=1m-1xj] （14）

[Σm-1=1m-2j=1m-1xj-μm-1xj-μm-1T] （15）

同理可得，对一个数据点进行删除操作后的高斯成分得到的新均值以及方差为：

[μm-1=mm-1μm-1m-1xm] （16）

[Σm-1=m-1m-2Σm-m-1mm-2xm-μm-1xm-μm-1T] （17）

1.2.4 高斯混合模型树的更新

高斯混合模型树的更新流程包括对相应父节点参数进行更新以及确认父节点是否具备裂变条件。对相应父节点参数进行更新的具体过程是：对数据进行安插或删除操作后，利用全部和数据安插节点来自于同一父节点的节点，对安插节点的父节点进行参数更新[7]，其中，主要参数是与父节点相应的高斯混合模型的平均值、方差以及权重等。确认父节点是否具备裂变条件的具体过程是：求出父节点中子节点的连通图数量，体现出父节点的连通度，同时也体现出高斯混合模型树与数据粘稠度[8]。两个高斯混合模型树间的距离可通过两个节点间的距离描述。若连通程度GQFD比阈值[Tdivide]高，则说明节点拥有较小的连通度，将该父节点分割成多个同其处于同层的新节点；否则当GQFD比阈值[Tdivide]低时，保持该父节点稳定不变。循环运行上述两个过程，直至根节点，完成高斯混合模型树的更新。

1.2.5 聚类结果的确定

本文基于类内距离和类间聚类两个指标，获取高质量的聚类结果。类内聚类越小，类间聚类越大，说明聚类效果越优。高斯混合模型树的非叶子节点描述了模型的数据分布情况[9]，高斯分布是最小的数据单元。基于高斯混合模型的相似度聚类公式，运算类内聚类和类间聚类公式为：

[IC=i=1M1≤p≤q≤kiGQFDGpi，Gqi] （18）

[IS=1≤i≤j≤MGQFDCi，Cj] （19）

式中：设置[C1，C2，…，CM]是[M]个聚类族，各聚类族表示一个高斯混合模型；[Gji]表示第[i]个聚类族内的第[j]个高斯成分；第[i]个聚类族相关的高斯数量为[Ki]。通过聚类质量CQ能够衡量聚类算法的聚类性能，表达式为：

[CQ=ICIS] （20）

类内聚类越低，类间距离越高，说明数据的聚类质量效果越佳。塑造完高斯混合模型樹后，基于CQ指标分析聚类效果的优劣，采用广度优先方法获取最佳的树节点作为最终的聚类结果。

2 实验结果与分析

2.1 有效性分析

实验采用本文递增聚类方法对菌群功能代谢通路以及表达基因两种类型大数据集进行聚类分析，检测本文方法的有效性。实验分析的菌群功能代谢KEGG数据库是常用的功能注释数据库，其是一种生物代谢通路分析数据库，其中包含了完备的代谢通路地图以及注释说明，其还具备KAAS等在线注释分析平台，基于用户提交的菌群蛋白序列，能够得到相应的KO注释信息，进而分析不同菌群样本的功能代谢。基于KEGG数据库的注释结果，采用本文聚类方法对注释结果实施聚类分析，获取菌群样本的功能代谢通路聚类情况，如图3所示，采用不同的颜色描述聚类结果。

采用本文方法实现芯片数据的聚类分析，采用的示例芯片数据来自于GEO数据库内GSE11787的Affvmetrix芯片的CEL文件，其中包括6个CEL文件、3个正常对照组以及3个HPS刺激组，是免疫器官脾脏的表达数据。读入原始数据后，采用AffvBatch目标将数据变换成ExpressionSet目标，为了提高差异表达基因的检测统计精度，采用本文方法对数据对过滤后的数据集实施递增聚类，聚类效果图如图4所示。

分析图3和图4的结果能够看出，本文方法实现了菌群功能代谢通路聚类以及表达基因的聚类，说明本文方法进行大数据集的数据聚类是有效的，具有较高的应用价值。

2.2 可扩展性和稳定性分析

大数据集具有动态性，稳定性好的递增算法能够确保在数据规模、特征维数以及聚类簇数量提高的状态下，将内存以及时间的消耗都控制在线性增长的维度，获取更为稳定的聚类效果，该稳定性确保算法具有较高的可扩展性。实验检测本文递增聚类方法同[k]均值聚类方法、EM聚类方法的可扩展性和稳定性结果，如图5～图7所示。其中的矩形图和曲线图分别用于描述不同方法的内存耗费和时间耗费情况。

对比分析图5～图7能够看出，无论在何种情况下本文方法的时间消耗和内存消耗都比其他两种算法低。同时随着数据规模、特征维度以及聚类簇个数的逐渐提高，本文方法的时间消耗呈现线性增长趋势，而其他两种方法却呈现指数增长趋势，说明本文方法在时间消耗方面具有较高的稳定性和可扩展性。本文方法需要进行旧节点的删除和新节点的生成操作，需要进行的操作较多，但是随着高斯模型树的增长，节点合并和删除，节点数量逐渐降低，使得本文方法的内存消耗低于其他两种算法。并且本文方法的内存消耗呈现线性增长，确保在内存消耗上本文方法具有较高的稳定性和可扩展性。

3 结 语

本文提出一种基于优先聚类和高斯混合模型树的递增聚类方法，先采用优先聚类算法对大数据集进行优先聚类，获取典型数据集，然后在典型数据集的基础上，采用高斯混合模型树的递增聚类算法获取最佳的聚类结果。

参考文献

[1] 卢志茂，冯进玫，范冬梅，等.面向大数据处理的划分聚类新方法[J].系统工程与电子技术，2014，36（5）：1010?1015.

[2] 张晓，王红.一种改进的基于大数据集的混合聚类算法[J].计算机工程与科学，2015，37（9）：1621?1626.

[3] 韩岩，李晓.加速大数据聚类K?means算法的改进[J].计算机工程与设计，2015，36（5）：1317?1320.

[4] 李斌，王劲松，黄玮.一种大数据环境下的新聚类算法[J].计算机科学，2015，42（12）：247?250.

[5] 向尧，袁景凌，钟珞，等.一种面向大数据集的粗粒度并行聚类算法研究[J].小型微型计算机系统，2014，35（10）：2370?2374.

[6] 马蕾，杨洪雪，刘建平.大数据环境下用户隐私数据存储方法的研究[J].计算机仿真，2016，33（2）：465?468.

[7] 冷泳林，陈志奎，张清辰，等.不完整大数据的分布式聚类填充算法[J].计算机工程，2015，41（5）：19?25.

[8] 周润物，李智勇，陈少淼，等.面向大数据处理的并行优化抽样聚类K?means算法[J].计算机应用，2016，36（2）：311?315.

[9] 龙虎，张小梅.基于修正二阶锥规划模型的大数据聚类算法[J].科技通报，2016，32（8）：168?171.