一种改进型逐点比较圆弧插补算法的FPGA实现

韩赛飞+施佺+刘炎华+黄新明+孙玲

摘 要： 逐点比较圆弧插补作为一种常见的插补算法在数控系统中广泛应用。为了进一步提高传统插补算法的速度，通过分析逐点比较法的特点简化了给进判别逻辑，提出一种改进的逐点比较圆弧插补算法实现方案。充分利用Verilog HDL语言特点，通过设计全局变量并使用FPGA丰富的内部逻辑资源实现了算法精度的可调。算法的FPGA硬件验证结果表明该实现方案具有运算速度快、插补精度可调和逻辑资源占用少的优点。

关键词： 圆弧插补； Verilog 硬件描述语言； FPGA； 逐点比较法

中图分类号： TN492?34 文献标识码： A 文章编号： 1004?373X（2017）19?0153?03

Implementation of an improved circular interpolation algorithm

with point?by?point comparison based on FPGA

HAN Saifei， SHI Quan， LIU Yanhua， HUANG Xinming， SUN Ling

（School of Electronic Information， Nantong University， Nantong 226019， China）

Abstract： As one of the common interpolation algorithms， the circular interpolation algorithm with point?by?point comparison is widely used in numerical control systems. In order to improve the speed of the traditional interpolation algorithm， the characteristics of point?by?point comparison method is analyzed to simplify the feed discrimination logic， and an improved implementation scheme of circular interpolation algorithm with point?by?point comparison is proposed. With the use of feature of Verilog HDL， the global variable is designed and the rich internal logic resources of FPGA are used to realize the precision adjustment of the algorithm. The results of FPGA hardware verification show that the proposed scheme has the advantages of fast computation speed， adjustable interpolation precision and little logic resource occupation.

Keywords： circular interpolation； Verilog HDL； FPGA； point?by?point comparison method

0 引 言

数控技术是工业制造的基础，数控机床在进行各种工件的轮廓加工时，一般都要用到插补算法[1]。插补算法根据起点、终点和半径等初始条件，实时计算工件加工过程中刀具移动的轨迹及其坐标值。数控插补算法主要有硬件和软件两种实现方法，其中，传统的硬件插补电路是由小规模数字电路模块搭建而成，不仅存在电路复杂、元器件多、体积和功耗大、可靠性低的不足，而且其加工速度和精度很难得到进一步提高[2?3]。而软件插补则受到计算机软件运算速度限制，插补的速度、精度等性能指标也很难满足高速控制要求[4?5]。随着“中国制造2025”实现制造强国战略目标的提出，数控技术必将迎来新的发展机遇和挑战，高速、高精度的插补算法实现技术则是核心之一。

目前，插补算法主要有逐点比较法[6]、数字积分法[7]和数字比较法[8]，其中，逐点比较法因为其控制精度高、算法简单成为在两轴插补系统中最常用的算法。借助FPGA芯片集成度高、工作速度快、逻辑单元功能强大，并具有灵活性高和可反复编程的特点[9]，本文针对现有逐点比较插补算法硬件实现的不足，提出一种改进的基于FPGA的算法实现方案。采用可综合的Verilog HDL语言完成了算法的硬件电路设计，给出了仿真验证与结果分析。

1 传统逐点比较圆弧插补算法

传统的逐点比较插补算法流程分为偏差判别、坐标给进、偏差计算和终点判别4步。

以图1所示的第一象限内一段逆圆弧为例，设其起点[S]的坐标为[Xs，Ys，]终点[E]的坐标为[E（Xe，Ye），][N（Xi，Yi）]为插补路径上的动点，圆心为原点[O（0，0），]半径为[R。]

为了表达动点[N]与理想圆弧之间的位置关系，引入偏差函数[Fi=X2i+Y2i-R2，]根据[Fi]的正负情况来判断动点是在圆内还是圆外，因此有如下插补规则：

（1） 当[Fi>0]时，动点在圆外，给进为[-ΔX。]

（2） 当[Fi=0]时，动点恰好在圆上，给进为[-ΔY。]

（3） 当[Fi<0]时，动点在圆内，给进为[+ΔY。]

上述插补规则只局限于第一象限的逆圆，表1归纳总结了实际插补中可能出现的其他象限和顺圆情况下的插补规则[10]，其中，[SRi]（[i=]1，2，3，4）代表第[i]象限的顺圆弧，[NRi]（[i]=1，2，3，4）代表第[i]象限的逆圆弧。

2 改进型逐点比较圆弧插补算法设计与实现

由表1可见，插补过程中首先需要判断偏差的正负，然后在确定的偏差情况下判断下一步给进[ΔX]或[ΔY]的多少。实现这一判别的直接方法就是通过多个条件语句依次进行，其不足是判别速度慢，也不利于算法实现中精度的提高。为此，本文提出一种简化给进判别条件的方法。

2.1 改进的算法设计

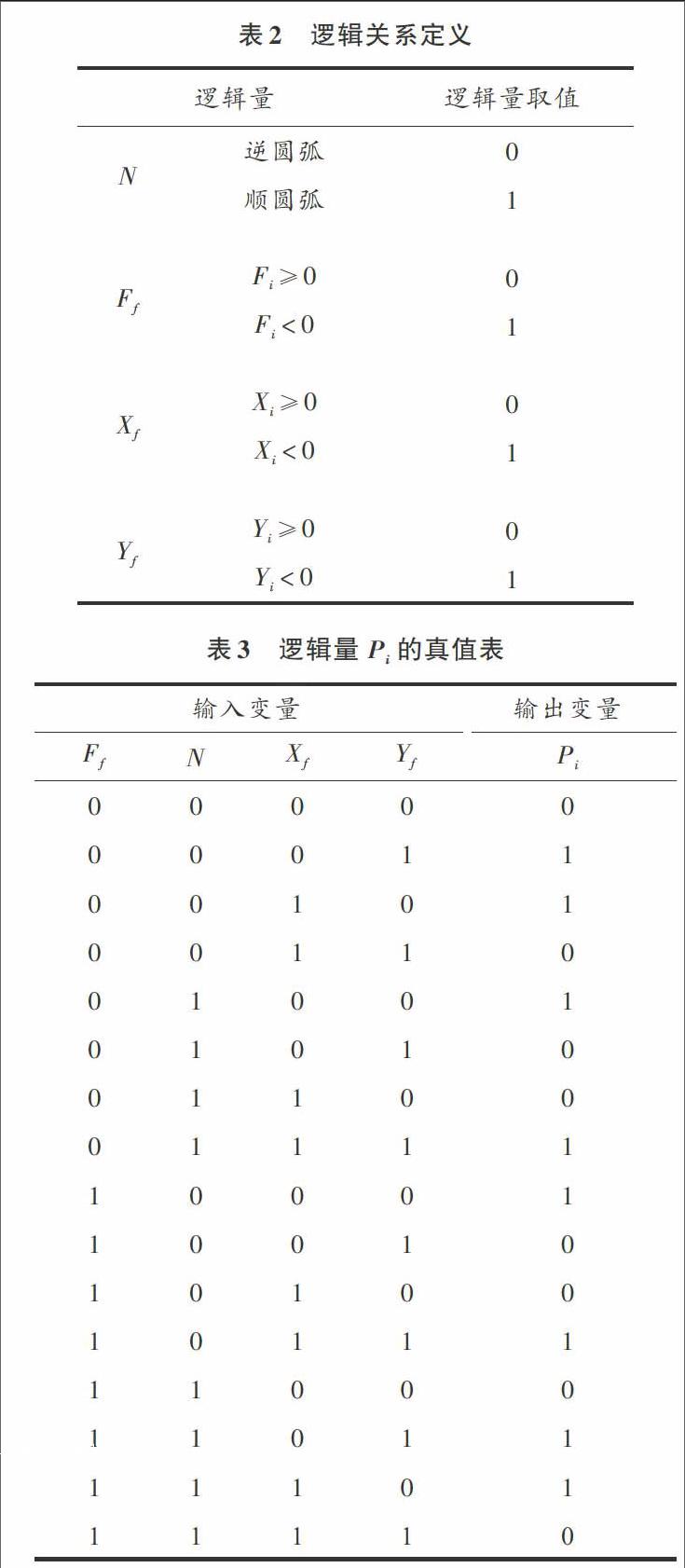
通过分析表1，本文将偏差判别函数分为大于等于“0”和小于“0”两种状态，并引入二进制逻辑，将表1中的所有情况定义为表2所示的逻辑关系。本设计还引入了一个新的逻辑变量[Pi，]规定[Pi=0]时，给进[X；][Pi=1]時，给进[Y。]根据上述分析条件，可归纳出如表3所示的[Pi]真值表。

由式（1）首先可以确定给进方向是[x]轴还是[y]轴，但无法判断给进的方向是正方向还是负方向，因此，需要再引入另外两个逻辑量[Fx]和[Fy，]并设定：当需要给进[x]的正方向时，[Fx=0；]给进[x]的负方向时，[Fx=1；]同理，当给进[y]的正方向时，[Fy=0；]给进[y]的负方向时，[Fy=1。]综合表1和表3可以得到[Fx]和[Fy]的逻辑表达式为：

[Fx=NYf] （2）

[Fy=NXf] （3）

通过式（1）～式（3）可以分别计算出[Pi，Fx]和[Fy，]从而可以确定动点下一步给进方向。

逐点比较法中，常通过比较动点和终点的坐标数值是否相等来判断插补过程是否完成。然而，当插补一个整圆时，起点的坐标和终点坐标相等。这种情况下，上述判别方法不再适用。因此，本文在程序设计中引入了一个标志寄存器[Q，]如果起点不等于终点，寄存器[Q]置0，插补程序正常执行；如果起点等于终点，寄存器[Q]置1，先停止一拍，在下一个触发脉冲到来时，寄存器[Q]置0，然后即可进行插补。本设计实现的改进型圆弧插补算法流程如图2所示。

2.2 改进的算法实现

根据改进后的逐点比较插补算法，在Quartus Ⅱ13.0和ModelSim 10.4软件平台下，本文完成了插补电路的可综合Verilog HDL语言设计，并进行了仿真验证。选用CycloneIV E系列EP4CE6E22C6器件的条件下，仿真得到的第一象限逆圆弧插补波形如图3所示。图中，输入的二进制起点横坐标[Xs]为00101，起点纵坐标[Ys]为00000；输入的二进制终点坐标[Xe，Ye]为（00000，00101）。en为使能信号，当[en=0]时，输入端有效。Sorn为路径方向信号，当Sorn=0时，进行逆圆弧插补；Sorn=1时，进行顺圆弧插补。x_out与y_out为输出的动点坐标；end_ f=1标志插补过程结束信号。

改进后的算法灵活性好，可以通过扩大输入起点、终点坐标以及半径的倍数来获得更多的步进点数，从而提高插补的精度。图4所示为步进点数为100的[14]圆弧的插补轨迹，从图4曲线可见，刀具的运动轨迹与理想圆弧的拟合程度较好。图5为起点坐标和终点坐标均为（50，0）的整圆插补轨迹。由于改进了终点判别条件机制，本文方案可以完成一个整圆的插补过程。

可见，本文改进后的圆弧插补算法在相同条件下占用的硬件资源较少，这是因为本文设计的算法省去了大量的条件判断语句，使得程序风格简洁，不仅节省了逻辑资源，也大大提高了算法的速度和效率。

3 结 语

本文提出一种基于符号条件位判别的改进型逐点比较圆弧插补算法，并进行了FPGA仿真验证。验证结果表明，仿真波形与理论分析一致。与传统的算法实现相比，本文方案具有插补速度快，占用资源少，插补精度高，输出脉冲稳定，硬件实现功耗低的特点，并解决了传统插补算法在起点与终点相同的情况下终点判别失效的问题，可应用于数控机床系统。

注：本文通讯作者为施佺。

参考文献

[1] 肖力.FPGA测试控制系统[D].北京：北方工业大学，2012.

[2] HAN Xingguo， WANG Binwu， WANG Weiqing. The research of open CNC system circular interpolation track based on kinetics and kinematics [C]// Proceedings of the Fifth IEEE Conference on Measuring Technology and Mechatronics Automation. Hongkong， China： IEEE， 2013： 1216?1218.

[3] 杨敬威.基于FPGA的数控硬件插补系统的研究与实现[D].西安：西安工业大学，2013.

[4] 张伟，王黎.基于FPGA的数字积分法插补控制器设计与实现[J].现代电子技术，2011，34（22）：150?153.

[5] 王汉霆.基于FPGA的运动插补控制芯片的研究与设计[D].武汉：华中科技大学，2009.

[6] 李莉，冯志永.数控系统中圆弧插补算法的改进和实现[J].控制与检测，2009（7）：61?62.

[7] 李存志，邢建国.比较积分法直线、圆弧插补方法的改进[J].机械设计与制造，2015（9）：185?188.

[8] 陈宏臣.基于FPGA技术的数控插补器算法改进研究[D].成都：西南交通大学，2010.

[9] 王诚.Altera FPGA/CPLD设计基础篇[M].北京：人民邮电出版社，2011.

[10] 席港港.传统逐点比较法直线插补方法的改进[J].山东理工大学学报，2012，26（1）：67?69.