断层突水非线性渗流-应力耦合研究
,,,
(山东科技大学 矿业与安全工程学院,山东 青岛 266590)
断层突水非线性渗流-应力耦合研究
郭惟嘉,赵金海,尹立明,江宁
(山东科技大学 矿业与安全工程学院,山东 青岛 266590)
针对断层水突出日益严重的问题,为揭示断层水突出过程中流固耦合作用影响下突水不同时刻、不同阶段的承压水运移规律,在断层破碎带中应用非达西流动方程并考虑应力作用和孔隙水压力作用对断层带中岩石力学参数的影响,应用Comsol软件建立含水层-断层-工作面三个阶段的断层导通前后达西-非达西-自由流动方程,获得应力-水压力作用下断层水突出及流动机理。结果表明:非达西Forchheimer方程能有效模拟计算高水压高流速水流在断层中的流动过程;流固耦合作用对断层中的非达西流动特性影响较大,断层破碎带作为含水层和工作面的连接部,其在应力作用下的渗透性突变是断层突水形成的根源。
采矿工程;断层破碎带;流固耦合;非达西流;突水
Abstract: In view of the increasingly severe fault water inrush, the non-Darcy flow equation was applied to the fault fractured zones and the effect of stress and pore water pressure on the mechanical parameters in the fault zone was considered so as to uncover the pressure-bearing water flow law at different moments and stages influenced by fluid-solid coupling in the fault water inrush process. The Comsol Multiphysics software was adopted to establish the Darcy-and-non-Darcy-and-free-flow equation before and after the fault breakover in the stages of aquifer, fault and working face, thus obtaining the fault water inrush and current flow mechanism under the effect of stress and water pressure. Results show that the non-Darcy Forchheimer equation can help to effectively simulate and calculate the flow process of current with high water pressure and high flow rate. The liquid-solid coupling has a significant influence on the non-Darcy flow characteristics in the fault. As the joint between aquifer and working face, the fault fractured zone will change abruptly in permeability under stress, which constitutes the root of fault water inrush.
Keywords: mining engineering; fault fractured zone; fluid-solid coupling; non-Darcy flow; water inrush
中国是矿井水文地质条件最复杂的国家,近年来随着矿井开采深度与强度的增加,底板突水问题更加严重。国内外学者对断层等构造突水问题进行了大量的研究。黎良杰等[1]分析了断层产生破坏、张开和冲刷的三种断层透水模式及突水模式相互转化的可能。李白英等[2-3]运用下三带理论,揭示了断层存在增加突水危险性的原因。罗浩等[4]分析了断层附近应力场变化的规律及水平构造力引起的断层下盘扭转现象。宋振骐等[5]将断层切割后的底板隔水层岩体视为悬臂梁结构,分析了留设的煤柱被压酥破坏后突水的全过程。上述方法从断层的产状、形成条件等方面对断层的赋存条件和水文地质条件进行了划分,分析了断层附近随煤层开采过程应力场的变化,指出了留设断层煤柱对防治断层突水方面的安全隐患,但未对含水层-断层-工作面中岩层运动过程渗透性受开采影响后的孔隙水在应力作用下的耦合过程和非线性渗流过程进行分析。
本研究将顶板-破碎煤柱-隔水层-含水层作为一个系统工程来考虑,分析水流从外界补给到含水层、在含水层中的达西渗流,断层、裂隙等破碎岩体中的应力-渗流耦合直至水流突破隔水煤柱进入开采工作面中的全过程,拟为预测断层突水水量和突水压力提供参考。
1 断层突水理论模型
1.1 含水层-断层-破碎煤柱-巷道的突水路径
断层是在复杂的地质构造作用下形成的,其材料强度相对较弱,开采过程中在断盘面附近易形成应力集中现象引发突水灾害。大量的断层突水事故表明,突水路径一般是沿着图1中三条突水路径涌入工作面,沿突水路径①突涌的必要条件是底板隔水层带发生破坏,不能起阻水作用。沿路径②突涌的必要条件是煤柱在上覆岩层作用下被压酥,支撑作用减小,煤柱中的孔隙、裂隙增加,孔隙率增大最终不能起到对承压水的阻水作用而发生突水。沿路径③突涌的必要条件是在路径②的前提下,破坏向上延伸,在顶板形成涌水裂隙。突水通道的形成是裂隙多通道并进,最终失稳的过程。岩体在应力作用下的材料性质变化在宏观上可以归结为孔隙率的变化,突涌过程也可视为承压水在破碎岩体等多孔介质材料中的运移过程。

图1 突水路径及边界条件
1.2 流场控制方程
目前描述流体在破碎岩体中的流动方程主要有达西和非线性渗流方程两大类。其中达西定律仅考虑压差作用和渗透性对流体流动的影响,适用于矿井水突出以前,含水层、岩体裂隙中的渗透流动,也可用于断层中的破碎带在完全活化以前,承压水在断层中的流动。当流体突破隔水层限制形成完整的水流路径后,流动呈现非线性变化,Darcy流不再满足该流动特征。
地下水在含水层中的线性达西层流流动,瞬态方程[6]可以表示为:

(1)
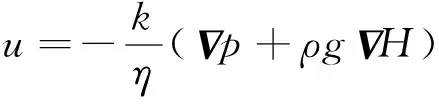
(2)
φ=φ0(1+cφ·Δp) 。
(3)

流体在工作面中的流动符合自由流动Navier-Stokes方程[7]:

(4)

(5)
其中,I为单位矩阵。
流体在多孔介质中的流动过程[8]介于达西层流和自由流动之间[9-11],渗流速度、水压力、固体骨架属性等方面的研究[12-13]是揭示非线性渗流的基础。基于理论和实验提出的Forchheimer方程,能很好的表现双重介质中的非线性渗流问题,适用于高速流体在断层破碎带中的流动[14],表述为:

(6)

其中,βf为Forchheimer曳力参数
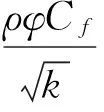
(7)
其中,Cf为流动过程中的摩擦系数,根据参考文献[12]表示为

(8)
突水通道形成以前,流体在含水层、断层以及破碎岩体中的流速较低,可应用达西定律近似求解。突水通道形成以后,断层破碎带中的渗透系数阶跃突增,流速明显增大,这时满足以动量方程为主导的Forchheimer方程。
2 数值模型的建立
2.1 Comsol Multiphysics软件简介
Comsol以有限元法为基础,基于偏微分方程组开发的多物理场耦合分析软件,用数学方法求解真实的物理现象[14]。以流动的连续性为基本方程,将Forchheimer非线性流动方程与Darcy线性流动方程和自由流动N-S方程耦合在一起,在含水层-断层、断层-破碎岩体、破碎岩体-巷道等交界面上分别满足水压相等和流速相等,求解断层突水问题。
2.2 模型建立及参数
各岩层力学参数如表1所示。

表1 模型初始力学参数
建立如图2所示的断层突水计算模型,模型长1 000 m,高400 m,其中底部含水层长1 000 m,高度为100 m,断层倾角45°,平均宽度为5 m,为含水断层,并贯穿整个模型。开采煤层厚度为5 m,工作面开采长度为600 m,开采步距20 m。底部含水层边界为进水流量边界,流速为4×10-3m/s,工作面边界为流体压力边界,压力为大气压0.1 MPa,含水层中流体粘性系数1×10-3Pa·s。
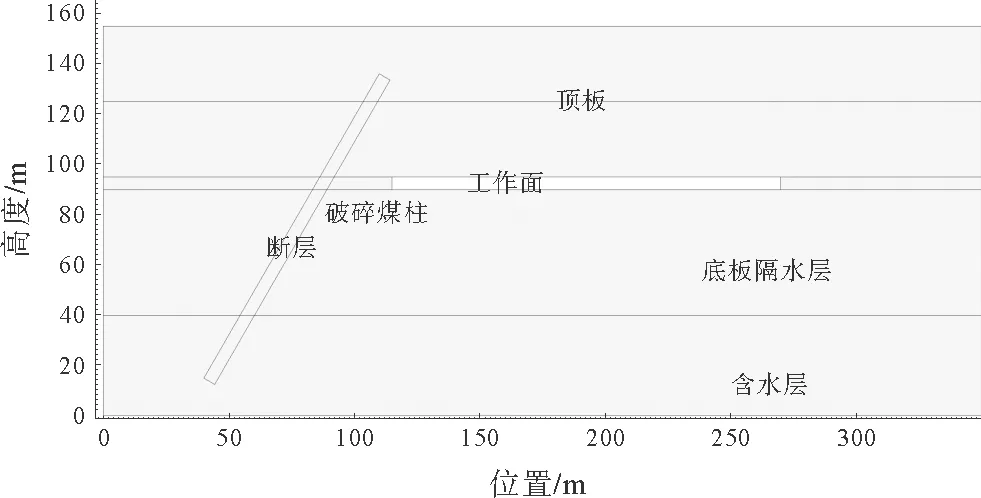
图2 断层突水的模型示意图
3 断层突水非线性算例分析
设置四种求解工况,分别模拟在突水通道形成前后的情况,揭示断层中的非达西流作用机制。其中,工况1表示形成突水通道以前,岩层中渗透率相同。含水层边界为恒定流量边界,入口流速为1×10-4m/s,Darcy区域和Forchheimer区域渗透率均为1×10-12m2;工况2表示形成突水通道以后,断层中渗透率增加10倍,入口流速为1×10-4m/s,Darcy区域渗透率为1×10-12m2,Forchheimer区域渗透率为1×10-11m2;根据初步预算结果,获得工况2条件下的边界压力为14.35 MPa,为便于对水压边界和速度边界进行比较分析,设置工况3和4的压力边界均为14.35 MPa。工况3表示形成突水通道以后,断层中渗透率增加10倍, Darcy区域渗透率为1×10-12m2,Forchheimer区域渗透率为1×10-11m2;工况4表示形成突水通道以前,岩层中渗透率相同, Darcy区域和Forchheimer区域渗透率均为1×10-12m2。
3.1 不考虑耦合作用时的渗流规律
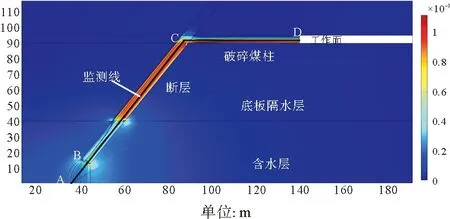
图3 不考虑流固耦合流速分布云图Fig.3 Distribution of the velocity field regardless of the fluid-structure coupling
图3 为不考虑流固耦合的流速分布云图,图4~5中显示了不考虑流固耦合作用时、四种工况下流体沿监测线A-B-C-D(图3)上速度变化和压力变化图。流速梯度的大幅度变化主要集中在断层(Forchheimer控制方程)区域,压力梯度的变化主要在含水层(Darcy控制方程)和断层中,但含水层中压降斜率更大。工况1中,含水层中最大流速为 7.5×10-4m/s,与断层交界面处的流速为 1.5×10-4m/s。进入断层后,流速逐渐增大,之后流速维持在3.9×10-4m/s,在断层与工作面交界面处,流速略

图4 监测线上流速分布曲线Fig.4 Flow rate distribution curveon monitoring line

图5 监测线上孔隙水压分布曲线
有降低,进入工作面自由流动区域后,流速逐渐恢复到3.6×10-4m/s。工况2中,在边界流速不变的情况下,断层区域渗透率提高10倍,在含水层中最大流速为 5.8×10-4m/s,进入断层区域后,流速略有降低,在含水层上边界发生阶跃变化,最大流速为1.7×10-3m/s,与工况1相比,流速增加3.2倍,之后流速维持在1.59×10-3m/s,与工况1相比流速增加4.1倍。
工况4中,在含水层区域最大流速为 5.5×10-4m/s,与断层区域交界面处的流速为 1.4×10-4m/s。进入断层区域后,由于Forchheimer方程考虑动能耗散作用,流速逐渐降低,在含水层上边界发生阶跃变化,在断层与工作面交界面处,流速略有降低,为1.05×10-4m/s,进入采空区自由流动区域后,流速逐渐恢复到1.5×10-4m/s。工况3中含水层最大流速为 6×10-4m/s,与断层区域交界面处的流速为 5.6×10-4m/s。进入断层区域后,流速略有降低,在含水层边界达到5×10-4m/s,在含水层上边界发生阶跃变化,最大流速为1.11×10-3m/s,与突水通道形成以前相比,流速增加6.5倍,之后流速维持在1.08×10-3m/s,与裂隙导通以前相比流速增加6.75倍。
承压水水压力变化方面,当断层与含水层渗透率相同时,从含水层到断层,孔隙水压由26 MPa降为22 MPa。断层渗透率增加10倍后,孔隙水压由14.35 MPa降为8.55 MPa,降低了1.68倍,表明断层和岩体中的渗透率增大,具有明显的降压作用。该模拟过程变化与杨天鸿等[15-16]的模拟结果相对应。
3.2 考虑流固耦合作用时的渗流规律

图6 不同覆岩压力下渗透率变化Fig.6 Permeability changes under different strata pressure
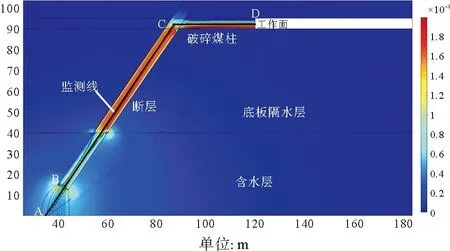
图7 考虑流固耦合流速分布云图
上述模拟过程中含水层和断层中的渗透率均设为恒定值,而固体场中应力的变化对岩体的渗透特性会产生较大影响。由于工作面(破碎煤柱)中的流体流动不受应力变化的影响,因此仅探讨含水层和断层中的变化,即监测线A-B-C上的变化规律。考虑流固耦合作用后,以覆岩压力为5和9 MPa为例(图6),断层带中的渗透率迅速增加为2.3×10-11和2.8×10-11m2,分别比初始渗透率增加2.3倍和2.8倍,在断层带中部位置,渗透率则呈现明显的下降趋势,此时主要是孔隙水压力的下降和应力集中的影响造成断层中渗透率的分区分布特性。在断层带与煤层交界处的岩层薄弱带,应力释放,达到渗透率的最大值。
对比图3、图7可知,流速、压力的变化规律与不考虑应力-渗流耦合作用时差别较大。覆岩(图1)压力为5和7 MPa时(图8),Darcy区域最大流速分别为 7.5×10-4和9.0×10-4m/s,与非耦合时相比分别增大1.3倍和1.6倍; 含水层与断层区域交界面处的流速为6×10-4和8.2×10-4m/s,分别增大1.3倍和1.8倍;进入断层区域后,流速逐渐增大,在含水层上边界发生阶跃变化,最大流速为1.2×10-3和1.65×10-3m/s,分别增大1.3倍和1.83倍。
承压水边界水压力恒定为12.3 MPa(图9),当断层与含水层渗透率相同时,从含水层区域到断层区域,孔隙水压由12.3降为7.15 MPa。而覆岩压力为5和7MPa时,孔隙水压分别降为7.3和7.05 MPa,曲线斜率增大,在含水层上方时斜率发生变化,水压下降也呈现明显的非线性变化。

图8 考虑耦合作用时不同覆岩压力下流速分布曲线Fig.8 Flow rate distribution curve under different strata pressure considering fluid-structure coupling

图9 考虑耦合作用时不同覆岩压力下压力分布曲线Fig.9 Pressure distribution curve under different strata pressure considering fluid-structure coupling
4 结论
在含水层、断层破碎带、工作面采空区中耦合应用Darcy、Forchheimer、Navier-Stokes三类水流运移方程,并与固体力学场耦合,分析了导水通道形成前后水流压力和流速变化特征,结果表明:断层作为含水层和工作面的主要导通区域,其应力状态下的渗透率的变化,对突水压力和突水流速的变化起关键作用;对恒定水压和恒定流量两种工况进行比较分析,恒定水压条件下,随断层中应力增大,渗透率在断层内部相对减小,而在断层带与煤层交界位置的应力释放区发生突增,孔隙水压力降增加,渗流速度增大,煤层开采到断层附近时应力释放,渗透率突增是诱发断层活化突水的主要原因。
[1]黎良杰,钱鸣高,李树刚.断层突水机理分析[J].煤炭学报,1996,21(2):119-123. LI Liangjie,QIAN Minggao,LI Shugang.Mechanism of water-inrush throughcaused by fault[J].Journal of China Coal Society,1996,21(2):119-123.
[2]李白英.预防矿井底板突水的“下三带”理论及其发展与应用[J].山东矿业学院学报,1999,18(4):11-18. LI Baiying.“Down Three Zones” in the prediction of the water inrush from coalbed floor aquifer-theory,new development and applicationof special mining technology in China[J].Journal of Shandong Institute of Mining and Technology,1999,18(4):11-18.
[3]魏久传,李白英.承压水上采煤安全性评价[J].煤田地质与勘探,2000,28(4):57-59. WEI Jiuchuan,LI Baiying.Security evaluation of coal mining above the confined aquifers[J].Coal Geology& Exploration,2000,28(4):57-59.
[4]罗浩,李忠华,王爱文,等.深部开采临近断层应力场演化规律研究[J].煤炭学报,2014,39(2):322-327. LUO Hao,LI Zhonghua,WANG Aiwen,et al.Study on the evolution law of stress field when approaching fault in deep mining[J].Journal of China Coal Society,2014,39(2):322-327.
[5]宋振骐,郝建,汤建泉,等.断层突水预测控制理论研究[J].煤炭学报,2013,38(9):1511-1515. SONG Zhenqi,HAO Jian,TANG Jianquan,et al.Study on water inrush from fault’s prevention and control theory[J].Journal of China Coal Society,2013,38(9):1511-1515.
[6]杨天鸿,师文豪,李顺才,等.破碎岩体非线性渗流突水机理研究现状及发展趋势[J].煤炭学报,2016,41(7):1598-1609. YANG Tianhong,SHI Wenhao,LI Shuncai,et al.State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass[J].Journal of China Coal Society,2016,41(7):1598-1609.
[7]黄玉萍,罗志强.Navier-Stokes方程自由面数值模拟(英文)[J].工程数学学报,2016,33(3):319-330. HUANG Yuping,LUO Zhiqiang.Numerical simulation of free surface for Navier-Stokes equations[J].Chinese Journal of Engineering Mathematics,2016,33(3):319-330.
[8]THAUVIN F,MOHANTY K K.Network modeling of non-Darcy flow through porous media[J].Transport in Porous Media,1998,31(1):19-37.
[9]SEDGHI-ASL M,RAHIMI H,SALEHI R.Non-Darcy flow of water through a packed column test[J].Transport in Porous Media,2014,101(2):215-227.
[10]李顺才,缪协兴,陈占清,等.承压破碎岩石非Darcy 渗流的渗透特性试验研究[J].工程力学,2008,25(4):85-92. LI Shuncai,MIAO Xiexing,CHEN Zhanqing,et al.Experimental study on seepage properties of non-Darcy flow in confined broken rocks[J].Engineering Mechanics,2008,25(4):85-92.
[11]CHERUBINI C,GIASI C I,PASTORE N.Bench scale laboratory tests to analyze non-linear flow in fractured media[J].Hydrology and Earth System Sciences,2012,16(8):2511-2522.
[12]黄先伍,唐平,缪协兴,等.破碎砂岩渗透特性与孔隙率关系的试验研究[J].岩土力学,2005,26(9):1385-1388. HUANG Xianwu,TANG Ping,MIAO Xiexing,et al.Testing study on seepage properties of broken sandstone[J].Rock and Soil Mechanics,2005,26(9):1385-1388.
[13]许凯,雷学文,孟庆山,等.非达西渗流惯性系数研究[J].岩石力学与工程学报,2012,31(1):164-170. XU Kai,LEI Xuewen,MENG Qingshan,et al.Study of inertial coefficient of non-Darcy seepage flow[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(1):164-170.
[14]AMIRI A,VAFAI K.Transient analysis of incompressible flow through a packed bed[J].International Journal of Heat & Mass Transfer,1998,41(24):4259-4279.
[15]杨天鸿,陈仕阔,朱万成,等.矿井岩体破坏突水机制及非线性渗流模型初探[J].岩石力学与工程学报,2008,27(7):1411-1416. YANG Tianhong,CHEN Shikuo,ZHU Wancheng,et al.Water inrush mechanism in mines and nonlinear flow model for fractured rocks[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(7):1411-1416.
[16]师文豪,杨天鸿,刘洪磊,等.矿山岩体破坏突水非达西流模型及数值求解[J].岩石力学与工程学报,2016,35(3):446-455. SHI Wenhao,YANG Tianhong,LIU Honglei,et al.Non-Darcy flow model and numerical simulation for water inrush in fractured rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(3):446-455.
(责任编辑:傅 游)
StudyonFaultWaterInrushMechanismandNonlinearSeepage-stressCoupling
GUO Weijia, ZHAO Jinhai, YIN Liming, JIANG Ning
(College of Mining and Safety Engineering, Shandong University of Science and Technology, Qingdao, Shandong 266590, China)
TD741
A
1672-3767(2017)06-0001-07
10.16452/j.cnki.sdkjzk.2017.06.001
2016-12-29
国家自然科学基金项目(51404144,51604167);山东科技大学研究生创新基金项目(SDKDYC170205)
郭惟嘉(1957—),男,山东济南人,教授,博士,主要从事矿井特殊开采和开采损害与环境保护方面的教学与研究工作.E-mail:wjguo@sdust.edu.cn 赵金海(1989—),男,山东潍坊人,博士研究生,主要从事矿山岩石力学与煤矿底板突水灾害控制的研究,本文通信作者.E-mail:363722411@qq.com

