新疆某黄土的土水特征及其分形描述

周跃峰，龚壁卫，周武华，刘 军

（长江科学院 水利部岩土力学与工程重点实验室，湖北 武汉 430010）

新疆某黄土的土水特征及其分形描述

周跃峰，龚壁卫，周武华，刘 军

（长江科学院 水利部岩土力学与工程重点实验室，湖北 武汉 430010）

本研究采用新疆某引水渠道边坡的黄土填料进行土水特征曲线试验，研究压实度和应力水平对土料的土水特征的影响规律。针对试验结果，本研究首先采用经典的van Genuchten模型进行曲线拟合。然后采用分形理论进行土水特征曲线的比较分析。结果表明：（1）随着压实度的增加，土水特征曲线向下移动；随着轴向应力的增加，土水特征曲线也会有所下移；（2）相应于孔隙分布，该土料的土水特征曲线具有明显的分形特性；（3）在相同压实度下，不同应力水平的SWCC分形拟合基本平行。采用本文所述的分形方法，在已知不同应力水平下的孔隙率时，可较为合理的从一个应力水平下的土水特征曲线推求其它应力水平下的土水特征曲线。

黄土；非饱和土；填料；土水特征曲线；分形

1 研究背景

新疆地域辽阔，地形复杂，工程建设被称为“稳疆兴疆”的基础工作，与人们生产生活紧密相关。近年来，新疆基础工程建设数量剧增，规模空前。工程活动改变了黄土的原生状态，也遇到了一系列新的问题。由于受到异常干燥、昼夜温差大等环境因素影响，新疆黄土从物源和后期成土环境等方面均与黄土高原的黄土存在较大差异［1］，非饱和黄土力学特性的研究成果亦少于其他地区。区域内某渠道工程部分区间为填方施工，采用当地黄土土料进行填筑（图1）。

工程施工所用黄土普遍处在非饱和状态（如最优含水率）下。土水特征曲线（SWCC）是非饱和土力学中描述土的非饱和状态对其水力、力学性质影响的一个重要指标，它在“含水率-吸力”平面中的位置和形状能够反映土中孔隙结构的特点以及土的持水能力。非饱和土力学中的多个研究领域，如强度理论、渗流理论、固结理论、本构理论都涉及到土-水特征曲线的应用。土水特征曲线作为非饱和土的一个重要指标，受多种因素影响。孙德安等［2］、李志清等［3］、周葆春等［4］等分析了孔隙比、密实度、干密度等对土水特征曲线的影响，提出孔隙结构是其重要影响因素。叶为民等［5］、卢应发等［6］、周跃峰等［7］研究了应力状态、干湿循环、结构破坏等因素对土水特征曲线的影响。分形几何的出现为建立非饱和土的水分特征曲线模型提供了理论基础［8］。分形方法所确定的土水特征曲线中的参数与土体本身的结构性质直接联系起来，具有明确的物理意义，是较为理想的方法，并已取得了一些有价值的成果［8-10］。

2 试验土料、设备及方案

2.1 试验土料试验土料取自新疆某渠道工程填方段的邻近开挖料场。土料特征为：黄色，较干燥，土质均匀，有少量虫孔及植物根茎孔洞存在。土料的级配采用筛分法与比重计法联合测试，得到该土料砂粒含量约28.2%，粉粒含量约60.5%，黏粒含量约11.3%，胶粒含量约5.5%。按《土工试验方法标准》（GBT50123-1999）［11］，在实验室内对土料进行击实试验，最优含水率及最大干密度分别为13%和1.82 g/m3（图1）。综合该土料的颗粒级配与液塑限分析，参照《土工试验方法标准》（GBT50123-1999），该土料应划分为粉土。

图1 土料的击实曲线

2.2 试验设备和方法土-水特征曲线采用Fredlund SWCC仪进行测定（图2）。Fredlund SWCC仪包括两个主要部件，分别为压力容器和压力仪表面板。容器是不锈钢结构，包括周期性冲刷和测量扩散空气的必要的管路和阀门。作为选件的气压加载架可以用来施加轴向应力。

图2 Fredlund土水特征曲线仪

该仪器可以在不同的轴向应力与基质吸力条件下测量土壤的土水特征曲线（SWCC）。采用15 bar的陶土板，该仪器可以控制基质吸力从0到1 500 kPa，并且能够对试样进行一维K0固结，然后使用一个土样来获得任意多个平衡数据点。

具体试验过程如下：（1）将准备好的试样放入环刀内，环刀下垫滤纸，放入盛水容器内吸水24 h进行饱和。（2）将试样小心放入Fredlund SWCC试验仪，在侧限K0条件下，通过配重施加轴向荷载。（3）在脱湿测试阶段，按照轴平移原理，逐级增加气压，每级气压下记录不同时间排水体积，直至趋于平衡，然后施加下一级气压。（4）气压达到目标值1 200 kPa并趋于平衡后，取出试样称重、烘干、再次称重，并进行不同吸力水平下土样含水率与饱和度的换算。

2.3 试验方案水利工程中，对土体的填筑密度常用压实度表示。土方填筑施工前参照土料的最大干密度和最优含水率进行控制，按设计干密度进行质量控制。填筑压实完成后，对碾压渠段进行干密度现场检测，检测过程严格按照《水利水电工程施工质量检验与评定规程》（SL176-2007）［12］执行。本项目渠道工程堤身设计填筑压实度不得小于0.95，填筑含水量控制在最优含水量附近，其上、下限偏离最优含水量在±1.5%以内。

由于土体在不同松密状态下的力学特性显著不同，为研究施工时土样正常压密和欠压密状态所展现的力学特性，试验中压实度Dc取0.86和0.96两个水平进行制样，对应的干密度分别为1.565和1.747 g/cm3。当地地质灾害通常为浅层滑坡，滑体最大厚度小于6 m，本研究中取3个较低的目标应力水平的进行测试，分别为轴向应力0、60和120 kPa，相对应的压实度为0.86的试验编号分别为SWCC086-1、SWCC086-2和SWCC086-3，压实度为0.96的试验编号分别为SWCC096-1、SWCC096-2和SWCC096-3。

试验结束后，根据基质吸力和含水率数据，进行土的质量含水率和体积含水率的换算，并结合不同吸力水平下的轴向变形校正体积含水率。按土的三相组成进行分析，土的体积含水率θ与质量含水率w关系如下：

式中：ρd为土的干密度，ρw为水的密度。

3 土-水特征曲线影响因素分析

3.1 应力水平的影响如图3所示，随着应力水平的提高，试验曲线逐渐向下移动，即在吸力相同时，轴向应力低的试样比轴向应力高的试样含水率高。当压实度Rc=0.86时，在饱和段，0 kPa压力下的含水率约比120 kPa轴压下高4%；在过渡段，三条曲线开始逐渐接近；当基质吸力为1200 kPa，该土体的吸力状态基本达到了残余段，含水率的最大差值约为2%。当压实度Rc=0.96时，试样在三级压力水平下的土水特征与Rc=0.86时试样所表现的规律基本一致。

图3 不同轴向应力下土-水特征曲线的比较

3.2 压实度的影响以轴向应力为0 kPa为例进行比较分析（图4）。在近饱和阶段，在吸力相同时，Rc=0.86的试样土水特征曲线明显高于Rc=0.96的试样。当基质吸力接近25 kPa时，两条曲线开始靠近，两个压实度下的各体积含水率的差值在1%以内。

图4 不同压实度下土-水特征曲线的比较（轴向应力为0 kPa）

当吸力大于25 kPa，压实度对土-水特征曲线的影响不明显。当基质吸力超过50 Pa时，压实度Rc=0.96的土水特征曲线略高于Rc=0.86的曲线，在两者相差不大时，应为前者较高的初始干密度按照式（1）换算所带来的影响。

4 土-水特征曲线的拟合与分形描述

4.1 土-水特征曲线的拟合由于实验室试验测得数据为离散点，需要做进一步分析，得到连续的土-水特征曲线，获取数值模拟或本构建模所需的基本参数。目前，有多个经验公式可用来描述土壤土-水特征曲线，包括：Brooks-Corey模型、Garden模型、van Genuchten模型、Fredlund&Xing模型等。其中，van Genuchten模型作为较有代表性的公式被广泛使用：

表1 黄土土-水特征曲线的van Genuchten拟合参数

式中：θ，θr，θs分别为体积含水率（满足θ=ϕs，即孔隙率ϕ和饱和度s的乘积）、残余含水率和最小吸力含水率；ua和uw分别为孔隙气压力和孔隙水压力；af，nf，mf为拟合参数。

采用式（2）对试验所得离散点进行拟合，各参数取值概括于表1。饱和含水率、残余含水率均随应力增加而降低，亦随密实度提高而降低。

4.2 土-水特征曲线的分形描述由Mandelbrot创建并发展的分形（fractal）理论已被广泛地应用于众多领域。大量研究表明，由形状与大小各异的岩土体颗粒和孔隙组成的孔隙介质具有分形特性。张季如等［9］，陶高粱等［10］推导出了三维空间内孔隙体积的分形模型，并通过实测数据进行了验证：

式中：V（＞r）为孔径大于r的累积孔隙体积；Va为土体总体积；L2为研究区域尺度；D为分维数。

按照Young-Laplace方程，基质吸力与有效孔径的关系可表征为：

式中：Ts为表面张力；α为接触角。在特定温度和土粒微观形貌下，2Tscosa为常数。

式中：A为包含表面张力、接触角与分维数的常数。

按照土的三相图与质量平衡关系，可推导出：

Dc=0.86的3个试验进气值在10～13 kPa，分维数2.754～2.760；Dc=0.96的3个试验进气值在15～21 kPa，分维数2.775～2.780。尽管对数坐标上的散点拟合可能带来进气值的一定误差，但仍可看出随着压实度提高，进气值亦有所提高；分维数随之提高。

基于前文不同压实度黏性土土-水特征曲线试验获得的试验数据作散点图，并进行线性拟合。表2给出了相应的拟合表达式、相关系数R2及计算所得的分维数D。计算获得的分维数随干密度增加，整体上呈增加的趋势。

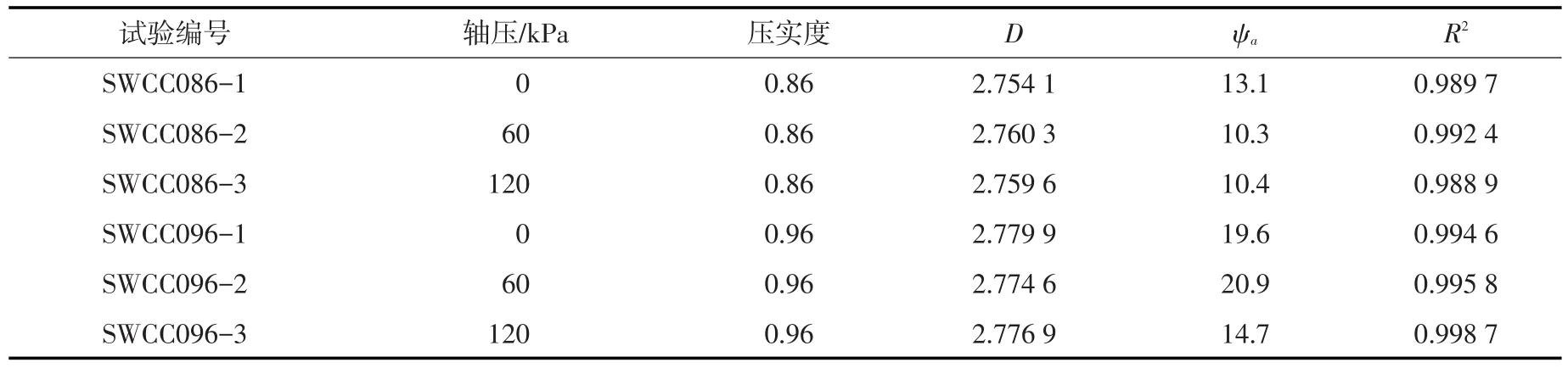
表2 各土-水曲线分维取值

已知土体含水率表示的土-水特征曲线，则以ln（1/Gs+w）为纵坐标、以-lnψ为横坐标作散点图，如果具有明显的线性部分具有分形特征，可根据斜率k求出分维数D=3-k。将本研究所得的6条土水特征曲线按上述分形方法绘制在图5中。在高于进气值的基质吸力水平下，土水特征曲线采用分形方法能够良好地线性拟合，相同压实度但不同应力水平下的拟合线基本平行。当压实度Rc=0.86时，分维数在2.754 1～2.760 3的范围内；当压实度Rc=0.96时，分维数在2.774 6～2.779 9的范围内。在低于进气值的区间，含水率接近固定值，可简化为水平线。

图5 不同压实度下土-水特征曲线的分形特征

5 结论

本文以新疆某渠道边坡黄土填料为对象，通过不同压实度和应力水平下的土水特征曲线研究，得出以下结论：（1）随着压实度的增加，土水特征曲线向下移动；随着轴向应力的增加，土水特征曲线也会有所下移。不同压实度下的土体，在吸力高于25 kPa时，土水特征曲线较为接近，含水率差值在2%以内。（2）相应于孔隙分布，该土料的土水特征曲线具有明显的分形特性，当压实度Rc=0.86时，分维数在2.754 1～2.760 3的范围内；当压实度Rc=0.96时，分维数在2.774 6～2.779 9的范围内。（3）相同压实度下，不同应力水平的SWCC拟合线基本平行。采用本文所述分形方法，在已知不同应力水平下的孔隙率时，可合理的从一个应力水平下的土水特征曲线推求其它应力水平下的曲线。

［1］ 徐张建，林在贯，张茂省.中国黄土与黄土滑坡［J］.岩石力学与工程学报，2007，26（7）：1297-1312.

［2］ 孙德安，孟德林，孙文静，等.两种膨润土的土-水特征曲线［J］.岩土力学，2011，32（4）：973-978.

［3］ 李志清，胡瑞林，王立朝，等.非饱和膨胀土SWCC研究［J］.岩土力学，2006，27（5）：730-734.

［4］ 周葆春，孔令伟.考虑体积变化的非饱和膨胀土土水特征［J］.水利学报，2011，42（10）：1152-1160.

［5］ 叶为民，白云，金麒，等.上海软土土水特征的室内试验研究［J］.岩土工程学报，2006，28（2）：260-263.

［6］ 卢应发，陈高峰，罗先启，等.土-水特征曲线及其相关性研究［J］.岩土力学，2008，29（9）：2481-2486.

［7］ 周跃峰，谭国焕，甄伟文，等.非饱和渗流分析在FLAC3D中的实现和应用［J］.长江科学院院报，2013，30（2）：57-61.

［8］ 徐永福，董平.非饱和土的水分特征曲线的分形模型［J］.岩土力学，2002，23（4）：400-405.

［9］ 张季如，陶高梁，黄丽，等.表征孔隙孔径分布的岩土体孔隙率模型及其应用［J］.科学通报，2010（27）：2761-2770.

［10］ 陶高梁，孔令伟，肖衡林，等.土-水特征曲线的分形特性及其分析拟合［J］.岩土力学，2014，35（9）：2443-2447.

［11］ 中华人民共和国水利部.GB/T 50123-1999土工试验方法标准［S］.北京：中国计划出版社，1999.

［12］ 中华人民共和国水利部.SL176-2007水利水电工程施工质量检验与评定规程［S］.北京：中国水利水电出版社，2007.

Abstract：In this research，laboratory tests were performed using an infilled loess material from a channel slope in Xinjiang，to investigate the soil-water characteristics of the material which are affected by the de⁃gree of compaction and the stress level.In this article，the classical van Genuchten’s equation was used firstly on the test results to obtain best-fitted curves.And then the fractal theory was adopted to conduct comparison between the SWCCS.Some conclusions are drawn below：（1）With the increase of the degree of compaction or the increase of the axis stress，the SWCC could move downward to some extent.（2） In contrast to the distributions of pores，the SWCCs of the material shows obvious fractal characteristics.（3）The curves of the SWCC from fractal fitting are parallel at different stress levels but the same degree of compaction.Adopting the fractal method suggested in this article，the SWCC could be predicted from a known curve.

Keywords：loess；unsaturated soil；infilled material；SWCC；fractal

（责任编辑：杨 虹）

The soil-water characteristics and the fractal feature of a typical loess in Xinjiang

ZHOU Yuefeng，GONG Biwei，ZHOU Wuhua，LIU Jun
（Yangze River Scientific Research Institute，Key Laboratory of Geotechnical Mechanics and Engineering of MWR，Wuhan 430010，China）

P642.3

A

10.13244/j.cnki.jiwhr.2017.04.011

1672-3031（2017）04-0308-06

2017-06-15

国家自然科学基金青年基金项目（51509018）；人社部留学人员科技活动择优资助项目（CKSD2016310/YT）；中央级公益性科研院所基本科研业务费项目（CKSF2016272/YT）

周跃峰（1982-），男，山西侯马人，博士，高级工程师，主要从事边坡工程与滑坡灾害研究，土的应力路径与剪胀性研究，非饱和土与特殊土研究。E-mail：zhou.yuefeng@163.com