利用化学势探究不同海拔的氧气浓度
王恒辰

摘要本文首先对玻尔兹曼能量分布律进行推导,之后通过利用玻尔兹曼能量分布律进行计算,推导出了氧气浓度与海拔的关系,并计算出不同海拔下氧气的浓度,应用MATLAB建立模型后得出不同海拔下氧气浓度,计算结果与实际情况基本相符。本文所提供的计算氧气浓度的方法,简单快捷。经分析表明,能够很好地与实际情况联系起来,最后提出了此种方法所存在的缺陷。
关键词玻尔兹曼能量分布律;MATLAB;不同海拔
氧气浓度的变化会对人类的生产、生活产生很大影响,研究不同海拔的氧气浓度很有必要。在测量不同海拔下氧气浓度时,可以利用氧气浓度测量仪进行实地测量,这种方法简单直接,可以测量得到实时数据,但是测量海拔较高时的氧气浓度就显得费时费力。也可以通过收集一瓶空气并与铜加热计算铜的增重,间接计算氧气的质量,进而计算出氧气浓度,但是这种方法误差较大,并且耗费资源。事实上,我们还可以利用化学势与玻尔兹曼能量分布律对不同海拔下氧气浓度进行计算。
化学势指的是物体所含有的能量,而微观粒子总是会从化学势高的相进入化学势低的相,从而降低系统的总自由能,并使系统达到平衡态。玻耳兹曼能量分布律是对化学势的一个补充,能够描述理想气体在受保守外力作用或保守外力作用不可忽略时,处于热平衡状态下的气体按能量分布的规律。
玻尔兹曼分布律是由玻尔兹曼提出来的。路德维希·玻尔兹曼(1844年2月20日一1906年9月5日),奥地利物理学家和哲学家,是热力学与统计物理学的奠基人之一,他发展了通过原子的性质来解释并预测物质的物理性质的统计物理学,并对热力学第二定律从统计意义上进行了阐述与解释。1869年,他通过将麦克斯韦速度分布律推广到保守力作用下的情况,得到了玻尔兹曼能量分布律。
玻尔兹曼能量分布律一般适用于处于平衡状态气体中的分子、原子。当粒子问的相互作用力可以微小到忽略不计时,液体、固体中的很多粒子同样适用玻尔兹曼能量分布律。因为其能描述在保守力场(如重力场)处于热平衡状态下的气体按能量分布的规律,所以我们可以利用该分布律导出不同海拔高度和气体分子密度(浓度)之间的关系。
利用玻尔兹曼能量分布律对不同海拔下的氧气/空气分子密度的计算,为本文中不同海拔下氧气浓度的模型提供了理论基础。在本文中,我们将会利用玻尔兹曼能量分布律计算不同海拔下的空气中氧气浓度,并和实际测得的数据进行对比分析,同时探索实践意义。
1玻尔兹曼分布律
一个物理系统内分子和原子运动造成了这个物理系统的温度变化。对于包含大量粒子的物理系统,麦克斯韦速度分布律很好地描述了这个系统里处于特定速度范围内的粒子数量。然而,当理想气体体系处于保守力场中,其气体分子的空间分布将会不均匀。玻尔兹曼分布律描述了处于热平衡和保守立场的理想气体体系在空间和速率上的分布
玻尔兹曼分布律是一个普遍的规律,当粒子间的相互作用力可以微小到忽略不计时,处于平衡状态气体中的分子、原子都适用玻尔兹曼能量分布律。因为其能描述在保守力场(如重力场)处于热平衡状态下的气体按能量分布的规律,所以我们可以利用该分布律导出不同海拔高度和气体分子体积密度之间的关系。
为参考位置的分子数量,在本文中设为海平面处的特定分子的数量,对分子运动速度进行积分,得所以在单位体积内的分子数量为
由此,我们可以得出在重力场中,单位体积气体分子数与海拔高度的分布规律。
2利用玻尔兹曼分布律对不同海拔下氧气浓度的计算
由玻尔兹曼分布律可知单位体积内,当海拔h升高,分子质量m增大时,n会减小。由此可知,当海拔升高时,单位体积内所有的气体分子数量将会减小,表示气压将会降低。而分子质量比较大的气体分子数将会比分子质量小气体分子数减小得更快,造成不同海拔下空气的组分比例变化,为氧气浓度的计算提供了可能。
我们可以分别计算出在海拔为h时单位体积内的氧气分子数量,再除以海平面处的空气“分子”密度,即为海拔h处的氧气浓度。
3利用MATLAB进行计算,并得出海拔与氧气浓度的关系图像
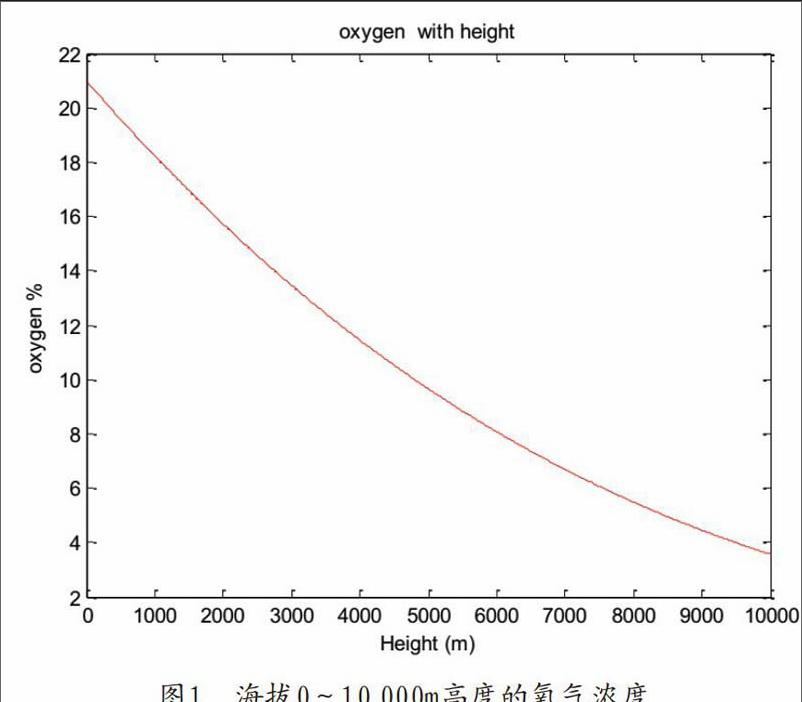
根据第二节的计算方式,利用MATLAB作图可以得到海拔与氧气浓度关系的图像如图1所示。
根据图l所示,在海拔高度0m~10000m内随着海拔的升高,氧气浓度会逐渐降低。当海拔为零时氧气浓度大约为21%,当达到10000m高空时,氧气浓度降至约3.8%。
4误差分析
根据第二节的计算过程可以得知,由于自然对数e为无限不循环小数,我们在公式中对于e的取值小于e本身的数值大小,因此计算值会小于真实值得到的结果;且地球的重力加速度的取值偏大,因此计算的结果会相对真实结果偏大;空气在海拔为零处的密度偏大,结果也会大于实际结果,同时,温度与海拔的关系相对来说取值较为偏大,因此我们得到的整体数据对于真实情况偏大一些。比如在海拔为零处值通过计算得到为21%,而实际情况下真实浓度20.8%。再加上由于计算过程是将空气处于理想状态下考虑得到的结果,而在实际生活中,由于人类活动的影响,比如说城市中汽车运行要利用氧气,同时会产生二氧化碳等气体,会导致结算的结果大于真实数据,再例如在森林等植被覆盖较多的地区,由于光合作用的影响,氧气浓度相对于结算结果偏高。再比如夏天由于太阳照射的影响,近地面温度偏高,近地面的空气上升导致近地面氧气浓度比正常值低。因此运用我们的计算得到的氧气浓度相对现实生活中氧气浓度存在一定量的误差。
5计算结果对实际的意义
实际生活中,有些工作人员以及普通游客会处于高海拔地区,比如去登山的游客、飞行员、跳伞运动员等,他们所处于的地区相对于低海拔地区的人来说,空气中氧气浓度更低,在氧气浓度为19.5%~23.5%之间时,属于正常浓度,对人几乎没有什么影响。当浓度处于19%时,会影响人的工作效率,甚至对人体头部、肺部以及全身循环系统产生一定影响。当氧气浓度处于14%~19%之间时,会使人呼吸急促、脉搏加快协调能力和感知判断力降低。当氧气浓度降低到10%~12%时,人们会出现呼吸急促,判断力丧失、嘴唇发紫等。当氧气浓度降低到8%~10%时,会使人智力丧失、昏厥、无意识、脸色苍白,恶心呕吐等。而当氧气浓度降低到6%~8%时大于等于8min,人100%死亡;6min,50%可能死亡;4min~5min,可能恢复。而当氧气浓度低于6%时,40s后,人会昏迷、抽搐,呼吸停止,死亡。氧气浓度过低时对人类的影响很大,因此,计算得到的结果虽然与实际情况存在误差,但可以反映出不同海拔下氧气浓度的大致情况,以便于人们在高海拔地区作业、游玩时做到适度的防备。
6结论
在本文中,我们通过利用玻尔兹曼能量分布律对不同海拔下氧气浓度进行了计算,由之前的计算结果可以得知,利用这种方法计算与实际情况的偏差不会很大,最主要的误差原因是低海拔下人类的活动。本文的计算方法,能够相对方便的计算出较高海拔下的氧气浓度,与利用氢气球实际测量等测量方式相比,本文方法成本相对较低、计算方式简单快捷,而且不需要動用十分复杂的仪器,因此,本文所介绍的计算不同海拔下氧气浓度的方法值得推广。endprint

