基于主动控制策略的智能完井生产优化
党 震,张 娇,王 浩
(1.西安石油大学,陕西西安 710000;2.陕西延长石油国际勘探开发工程有限公司,陕西西安 710000;3.宿迁职业技术学院,江苏宿迁 223800;4.江苏双星彩塑新材料股份有限公司,江苏宿迁 223800)
基于主动控制策略的智能完井生产优化
党 震1,2,张 娇3,王 浩1,4
(1.西安石油大学,陕西西安 710000;2.陕西延长石油国际勘探开发工程有限公司,陕西西安 710000;3.宿迁职业技术学院,江苏宿迁 223800;4.江苏双星彩塑新材料股份有限公司,江苏宿迁 223800)
为充分发挥油藏数值模型在生产预测方面的作用,从而指导智能完井生产优化方案的制定。本文以油藏数值模型为载体,结合数学最优化算法,研究了在水平非均质油藏中智能完井的有效价值。同时为寻找一种高效的、稳定的优化算法,本文借助MATLAB优化工具箱研究了序贯二次规划最优化算法在智能完井生产优化中的应用。
智能完井;主动控制;生产优化
智能完井主动控制策略是指:在当前油藏油气分布下,将油藏整个生产周期划分为多个优化周期,运用油藏数值模拟技术和数学最优化原理,以油田的净现值或采收率作为目标函数,通过优化各阶段的井下控制阀阀孔的打开面积,从而得到一套最佳的油田生产方案[1]。
主动控制策略由于在油田未见水之前,就对井下控制阀进行调控,在理论上来说可以获得相对于被动控制更高的净现值,延缓出水的时间,降低出水的速度,但是主动控制需要巨大的计算量。例如将油井生产周期划分为10个时间段,即在油井生产周期内共调节了10次控制阀,若一口井安装了4个井下控制阀,此时单井的控制变量达到了40个,对于含有多口油井的油田来说,优化的自变量将达到数百以上,为了获得最优结果,优化过程耗费很长的时间,下文将对比各算法的最优结果,并讨论算法的优化效率。
1 优化算法与数值模型相结合
为实现智能完井主动控制优化生产,关键是要将数学优化算法与油藏数值模型之间结合。主动控制策略的调节变量是智能完井井下控制阀阀孔的面积,同时将油藏的最终采收率或净现值作为目标函数[2],其数学形式如下所示:

式中:将NPV作为目标函数,t为时间节点。如将优化周期划分为10段,则N=10。d为折现率,即将未来产生的利润折算成现在的价值,随着时间的增加,同等利润折算成现在的价值也会越来越低。当考虑未来油价的不确定性等因素时,折现率将变得不是很重要,本文中在计算净现值时将不再考虑折现率的问题。Oil Prince表示原油价格,本文中取 300$/m3,Water Handling Cost表示水处理价格,本文取18$/m3。
油藏数值模拟器在控制系统中等同于“黑箱”的作用。所谓“黑箱”即向系统输入一组变量,系统会返回一个相对应的结果,无需去了解系统内部的计算过程,只要获取系统的反馈结果。油藏工程师不需要求解压力和饱和度的差分方程,把油藏数值模拟看做黑箱系统,优化算法将变量输入到数值模拟之后,油藏数值模拟器输出所需的日产量和井底压力。本章选用MATLAB作为编程工具,其内置的优化工具箱可以解决多种有类型的优化问题,同时操作方便,效率高[3]。
2 人工验证模型
本文仅采用简化模型作为研究对象,该模型中的数据通过Eclipse自带的练习数据包演化而来,即反映一些典型的地层非均质特征的人工模型,储层构造简单,对地质的描述准确,不存在不确定性问题。本章以该模型为对象,研究智能完井水平井在平面非均质性油藏中的最优生产方案[4]。
该模型顶层深度为2500m,初始油藏压力为26MPa,油藏的水平方向渗透率分布图(见图1),图中红色区域为高渗带,表示油藏中的裂缝。在油藏开发初期方案中,水平井的井筒方向与地层主裂缝方向是垂直的,构成双重孔隙系统,这样有利于地层中的流体流出,但是在后期注水开发过程中,裂缝将造成水体前缘前进速度加快,易造成整个井筒处于水淹状态。该模型的渗透率分布情况(见表1),将模型分为4个区域,每个区域的渗透率属性都存在较大差异。在生产约束方面,生产井P1采用定日产液量的控制方式,目标日产液量为500 sm3,最小井底流压为20MPa,注水井采用恒压注水的方式,井底压力保持30MPa。

图1 油藏水平渗透率分布示意图

表1 模型水平渗透率及孔隙度分布
2.1 传统完井方式油井生产状况
在生产了1000 d之后,传统完井方式的油藏剩余油分布(见图2)。正如预测的一样,高渗带中水体突破速度快,使得油井含水率急剧升高,但是低渗带的剩余油饱和度依然较高,生产井P1的含水率变化曲线(见图3),在生产了500 d左右,高渗带的水体突破,造成P1的含水率从0%直接上升到55%,生产900 d之后,含水率达到了65%左右,水平井P1面临关井的问题。当前我国部分油田,由于构造和裂缝的复杂性,水平井在生产一段时间之后,面临着严重水淹的问题,因此如何解决该问题,成为当前研究的热点。
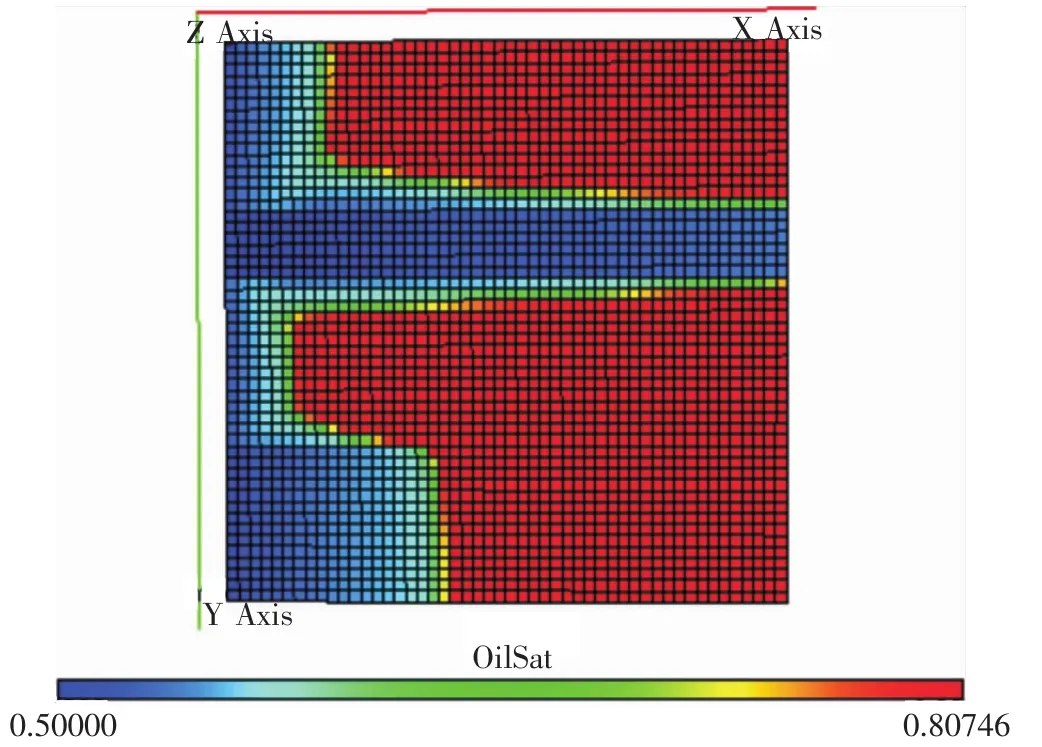
图2 传统完井方式剩余油饱和度分布

图3 传统完井方式生产井含水率变化曲线
3 SQP算法简介
序列二次规划(Sequential Quadratic Programming,SQP)最先由Wilson于1963年在其博士论文中提出,该方法特别适用于非线性约束规划问题,算法的基本思想是在迭代点附近用近似的二次规划模型替代原始模型并求解,然后以一系列二次规划的解逼近最优解[5,6]。
原始问题的模型可表述为:
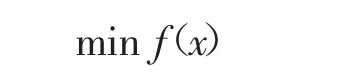
s.t.gi(x)≤0,j∈I,I为正整数集合{1,2,…,m}。
其中,子问题为原始问题的近似,其模型为:
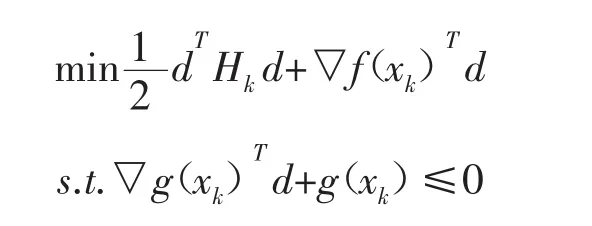
设当前的迭代点为xk,通过求解子问题可以得到dk及其相应的Lagrange乘子λk,同时令下一个迭代点xk+1=xk+dk。
3.1 SQP算法应用
MATLAB优化工具箱中的SQP算法,具有简洁的界面操作,省去了算法设计和编写过程。优化的模拟过程(见图4),采用SQP算法优化控制阀的面积时,共需要调用305次油藏数值模拟器,经过7代的迭代即收敛到优化结果。主动控制策略将生产周期分割成很多阶段,使得优化变量大大增加,但是SQP算法展现了快速收敛速度,较低的优化时间,大大提高优化效率。

图4 SQP算法优化过程和结果
4 模拟结果
模式搜索算法优化后累积生产结果与传统结果的对比(见图5),图中红色曲线代表智能完井方式的生产结果,蓝色表示传统完井方式的累积生产结果。经过1000 d的生产后,P1井的累积产油量为415502.52 m3,比传统完井方式360215.19 m3增长了15.35%;累积产水量为84657.156 m3,比传统完井方式的139784.81 m3降低了39.44%;累积净现值为1231.27×105美元,比传统完井方式的1055.48×105美元增长了16.65%。从出水时间来看,其优化方案并没有推迟水体的突破,但是从总体优化效果来看,SQP算法仍然带来了很大的收益。
如图6所示,(a)图为智能完井方式油藏剩余油饱和度分布图,(b)图为传统完井方式的剩余油饱和度,两图对比可以清晰地看出,智能完井方式下的油藏高渗带流体推着低渗带的油向两侧流动,高渗带的含水饱和度也低于传统完井方式的含水饱和度,同时第4渗流带的油水前缘也向前推进的一段距离,采用主动控制策略在生产了1000 d之后,P1井的含水率在0.45,而传统方式的含水率为0.62,降低了油井的含水率,提高油藏的采收率。因此,SQP算法在解决智能完井主动控制生产优化问题是有效的。

图5 SQP优化后累积产油量和累积产水量与传统完井对比
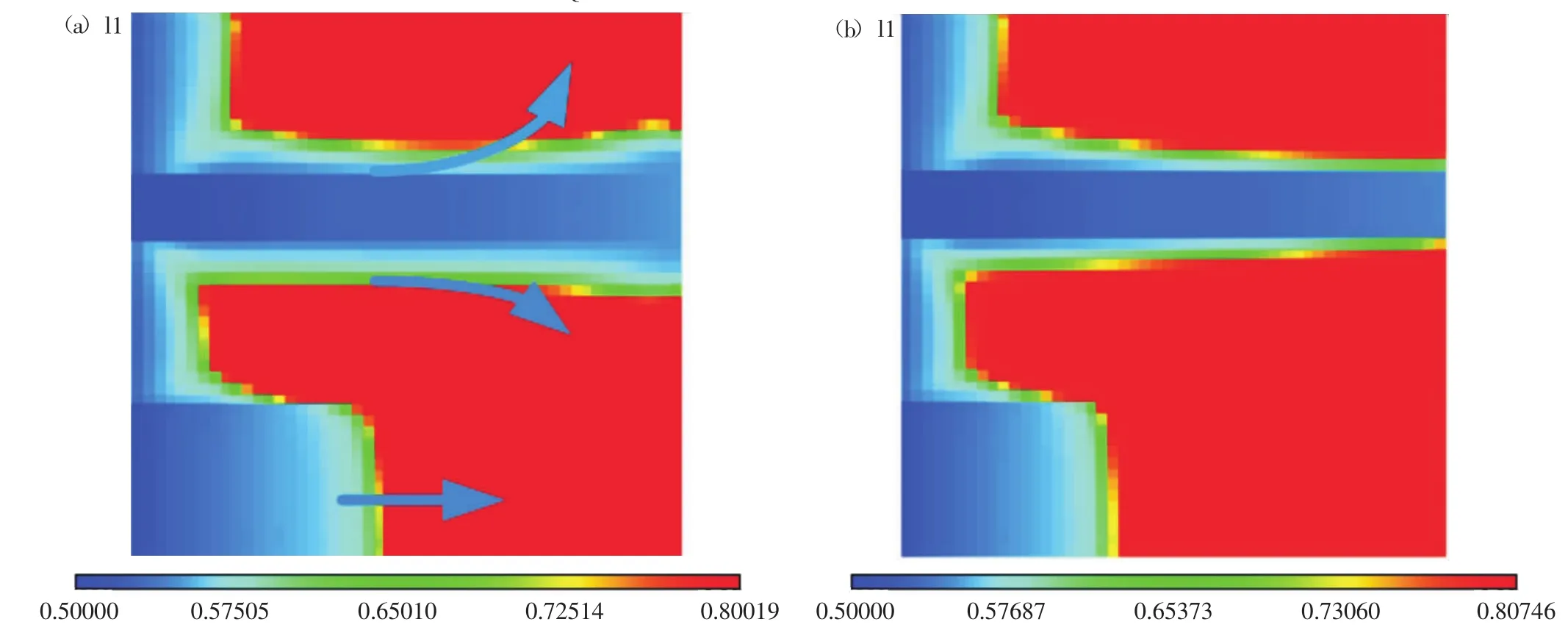
图6 智能完井和传统完井剩余油饱和度
[1]Brouwer D.R.and Jansen J.D.Dynamic Optimization of Water Flooding with Smart Wells Using Optimal Control Theory[R].SPE 78278,2002.
[2]Carvajal,G.A.,Boisvert.I.,Knabe,S..A Smart Flow for Smart Wells:Reactive and Proactive Modes[R].SPE 167821,2014.
[3]Kai Sun,Boyun Guo,Luigi Saputelli.Applying Multi-Node Intelligent Well Technology for"Active"Control of Inflow Profile in Horizontal/Inclined Wells[R].SPE130490,2010.
[4]王子健.基于最优控制理论的智能井动态优化技术[J].石油学报,2012,33(5):887-891.
[5]石国春.关于序列二次规划算法求解非线性规划问题的研究[D].兰州:兰州大学,2009.
[6]张奇.非线性约束条件下SQP算法研究[D].青岛:青岛大学,2008.
Optimization of intelligent completion production based on active control strategy
DANG Zhen1,2,ZHANG Jiao3,WANG Hao1,4
(1.Xian Shiyou University,Xi'an Shanxi 710000,China;2.Shanxi Yanchang Petroleum International Exploration and Development Engineering Co.,Ltd.,Xi'an Shanxi 710000,China;3.Suqian Vocational and Technical College,Suqian Jiangsu 223800,China;4.Jiangsu Shuangxing Colour Plastic New Materials Co.,Ltd.,Suqian Jiangsu 223800,China)
In order to give full play to the role of reservoir numerical model in production prediction,it is necessary to guide the development of intelligent completion production optimization scheme.Based on the reservoir numerical model and the mathematical optimization algorithm,this paper studies the effective value of intelligent completion in horizontal heterogeneous reservoirs.At the same time,in order to find a highly efficient and stable optimization algorithm,this paper uses MATLAB optimization toolbox to study the application of sequential quadratic programming optimization algorithm in intelligent completion optimization.
intelligent completion;active control;production optimization
TE319
A
1673-5285(2017)09-0035-04
10.3969/j.issn.1673-5285.2017.09.009
2017-08-28
党震,西安石油大学在读研究生,长期从事智能完井研究工作。

