基于SPH方法的非均质煤层瓦斯渗流模拟

， ，，

(山东科技大学 矿业与安全工程学院,山东 青岛 266590)

基于SPH方法的非均质煤层瓦斯渗流模拟

程国强，赵芳，明德志，谭云亮

(山东科技大学 矿业与安全工程学院,山东 青岛 266590)

基于煤层瓦斯渗流方程，通过虚粒子法处理边界条件,提出了一种对非均质煤层瓦斯瞬态渗流进行模拟的光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法。煤层存在三个典型的非均质性:(a)沿煤层走向的非均质性,(b)Weibull随机分布的非均质性,(c)是(a)和(b)两种情况都存在的非均质性。结果表明:通过SPH方法得到的数值模拟解与解析解一致,三种非均质煤层都会导致瓦斯渗流的非线性行为。而瓦斯流动的非线性程度与煤层的非均质性参数m和n有关。该数值模拟提供了一种揭示煤层中瓦斯渗流和瓦斯灾害非线性行为机理的有效方法。

光滑粒子流体动力学;瓦斯;非均质;虚粒子;非线性

Abstract: Based on gas seepage equations, a smoothed particle hydrodynamics (SPH) method was proposed by dealing with boundary conditions through virtual particle for the purpose of gas transient seepage simulation in heterogeneous coal seam. Three typical heterogeneous conditions were considered, namely, (a) heterogeneity along coal seam strike, (b) heterogeneity of Weibull random distribution, and (c) heterogeneity of integration of both (a) and (b). The results show that the numerical solution obtained by the SPH method is consistent with the analytical solution and that all the three kinds of heterogeneous coal seam can result in the nonlinear behavior of gas flow. The nonlinearity degree of gas flow is correlated tomandn, the two heterogeneity parameters of coal seam. The simulations provide an effective approach for revealing the mechanisms of the nonlinear behavior of gas seepage and gas disasters in coal seam.

Keywords: SPH; gas; heterogeneous; virtual particles; nonlinear

It is necessary to study the migration characteristics of gas in coal seam to establish a perfect gas seepage theory system and to explore the outburst mechanism of coal and gas[1]. At present, the research on gas seepage in coal seam has already formed the Darcy flow theory, the non-Darcy flow theory, the solid-gas coupling theory and the earth physical field effect theory[2-5]. Darcy flow theory uses Darcy’s law to deduce the gas seepage equation in homogeneous coal seam, which provides a theoretical basis for the study of gas seepage law[6]. However, as a special kind of porous medium, coal has a complicated fracture development and occurrence state. As a result, the gas seepage in coal is not consistent with the simulation results under the Darcy flow theory. Based on large numbers of experimental studies, the power law theory of gas flow in homogeneous coal seam, that is, the non-Darcy flow theory, was proposed by Japanese scholars. Sun[7]extended power law to heterogeneous anisotropic coal seam, and established a nonlinear gas flow model. Power law has guiding significance for the research and development of nonlinear gas flow theory. With further understandings of gas flow, many scholars have studied the nonlinear gas flow from the angle of solid-gas coupling and the geophysical field[8-9]. All of these studies are based on the homogeneous coal bed, and the Darcy’s law is modified to establish and develop the corresponding flow model and numerical method[10]. However, coal is a heterogeneous porous medium and the studies on the nonlinear seepage flow caused by heterogeneity is relatively fewer[11].

As a basic property of coal body, heterogeneity is usually described by the change of permeability coefficient, one of the important parameters which can reflect the difficulty of gas seepage in coal seam. Therefore, the heterogeneity of coal body has an important influence on the gas flow. The nonlinear seepage mechanism caused by the coal body’s own property is studied, which is a necessary precondition to further study the influence of solid-gas coupling, multi-physical field effect and other factors on gas seepage.

At present, the finite element method is widely used in the numerical simulation of gas flow in coal seam. However, it is difficult to obtain the subtle interaction mechanism between gas molecules with the finite element method. Smoothed particle hydrodynamics method (SPH) is an adaptive meshless particle method[12], which was initially used to solve three-dimensional open space astrophysics problems. Now, the SPH method has been applied to many fields such as solid mechanics, fluid dynamics, explosion, high speed impact, material dynamic response and so on[13-16]. With this method, a series of particles can be used to describe the problem domain and obtain interaction force between particles by solving the integral equation and partial differential equations.

This paper uses SPH numerical method to establish the gas seepage model of coal seam, and simulates typical heterogeneity of coal seam by changing the permeability coefficient of particles. The law of gas flow in coal seam based on Darcy’s law is obtained, and the nonlinear seepage mechanism caused by the heterogeneity of the coal body is revealed.

1 The basic principle of SPH method

Initially used to solve three-dimensional open space astrophysics problems, the SPH method has now been applied to several fields such as solid mechanics, fluid dynamics, explosion, high speed collision, and material dynamics response. In SPH method, problem domain is represented by the randomly-distributed particles and the result of the continuous functionA(x) is estimated by the summation of series of discrete points. The construction of its equation includes kernel and particle approximations of field function. The basic principle of SPH method is shown in Figure 1.Integral expressions of functionA(x) and its derivative can be written as:

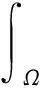
(1)

(2)

Particle approximation expressions of functionA(x) and its derivative can be written as:

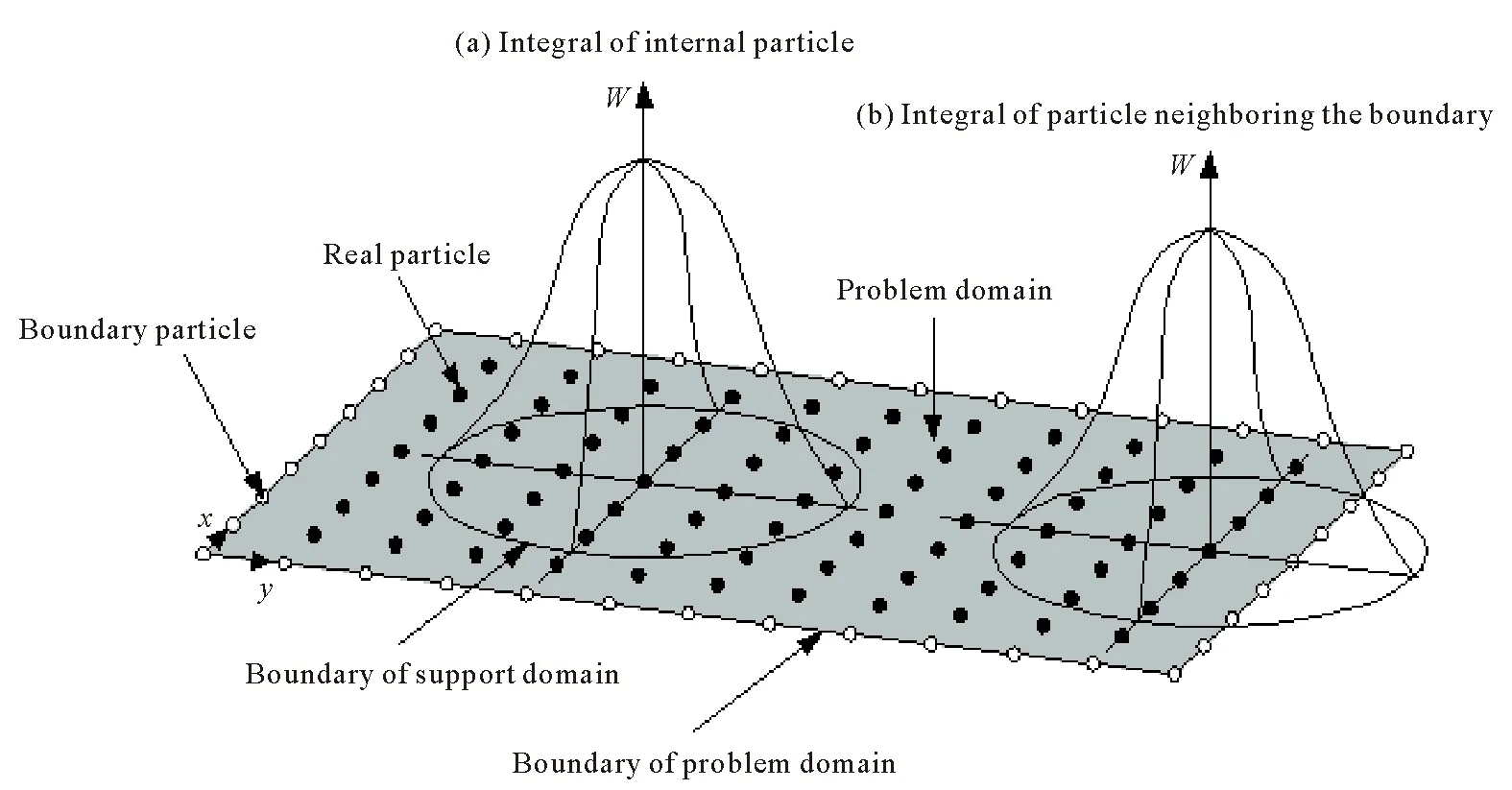
Fig.1 Schematic description of SPH method

(3a)

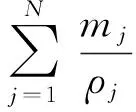
(3b)

WhereΦis kernel function,his the influence area of kernel functionΦ，mjis the quality of particlej,ρjis the density of particlej. We use the cubic spline kernel function:

(4)

whereR=rij/h,rijis the distance between two particles.

In SPH method, the particles in boundary or near the border will cause integral error because kernel functionΦis truncated by boundary, as shown in Figure 1(b). In this paper, we apply the virtual particle method to solve the problem of boundary defects in the simulation of gas seepage in coal seam. The gas pressure values of the virtual particles are determined by the real particles and the boundary particles.Moreover, the virtual particles having the same properties with real particles were arranged outside the problem domain to compensate the integral error caused by the missing boundary particles.

2 Establishment of gas seepage model

2.1 Gas seepage control equation in coal seam

Gas seepage control equation (7) in coal seam is established according to gas content equation(5), law of mass conservation and gas flow which obey the Darcy law.

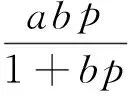
(5)

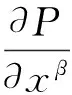
(6)

(7)

where

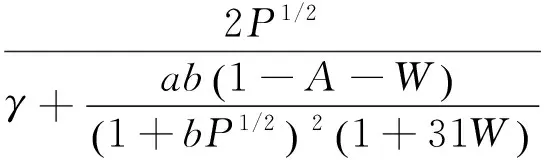
(8)

whereXis gas content,γis the porosity of coal,a,b,W,Aare parameters of coal seam,Pis gas pressure, andP=p2·λβ,qβare permeability coefficient and gas flow quantity along theβdirection respectively.

2.2 The SPH discrete of gas seepage equation

By applying the SPH particle approximations, equation (6) and equation (7) can be expressed as:

(9)

(10)

2.3 SPH model for gas seepage simulation

As a simulation example, a coal seam region of 10 m in width and 1 m in height was selected. The size of physical model and the arrangement of particles are shown in Figure 2. Values are as follows:h=0.025 1 m,n=10%,a=27 m3/t,b=0.7 MPa-1,W=3%,A=20%,p0=1 MPa,p1=0.101 325 MPa.

Coal medium behaves heterogeneously throughout the process of gas seepage. This heterogeneity is partially caused by the mining pressure. This contributes to increasing permeability coefficient with decreasing distance from the coal wall. Meanwhile, the permeability coefficient also shows random distribution in directions where the thicknesses of coal seam are the same. Therefore, the expression of permeability coefficient is expressed as

(11)

whereλ0is the original permeability coefficient of coal seam,xis the distance from the working surface,x0is the influence range of broken zone of coal wall,ζis the random number,nis heterogeneous degree,mandkare coal parameters.

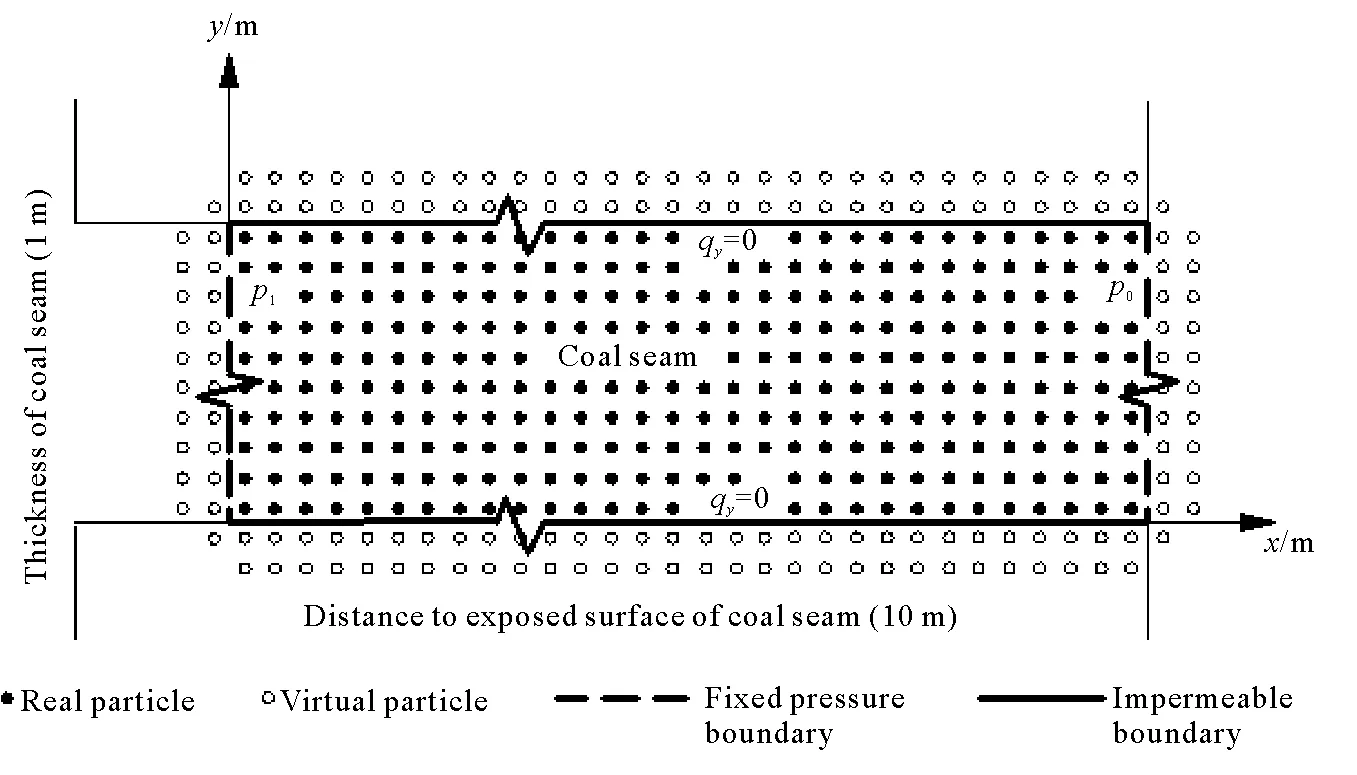
Fig.2 SPH model for gas seepage simulation

3 SPH numerical simulation of gas seepage in homogeneous coal seam

Whenm=0 andk=0, the model indicates homogeneous coal seam. Permeability coefficient of homogeneous coal seam isλ=1 m2/(MPa2·d) in the following numerical simulation of gas flow. TakingPtoP0in equation (7) for the problem of one-way seepage in homogeneous coal seam, and then considering analytical solutions of gas pressure, gas emission quantity in coal wall are calculated by

(12)

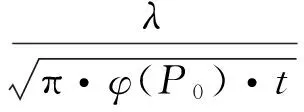
(13)

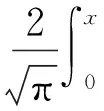
SPH numerical simulation of gas seepage in homogeneous coal seam is conducted by using gas seepage equation whose coefficient isφ(P0). We applied the same parameter to solve equations (9) and (10) in order to obtain analytical solutions of gas pressure and gas emission quantity in coal wall. Simulation results were processed by pressure criterion, flow criterion, time criterion and distance criterion, as shown in Figure 3.

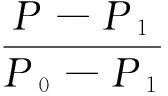
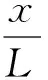
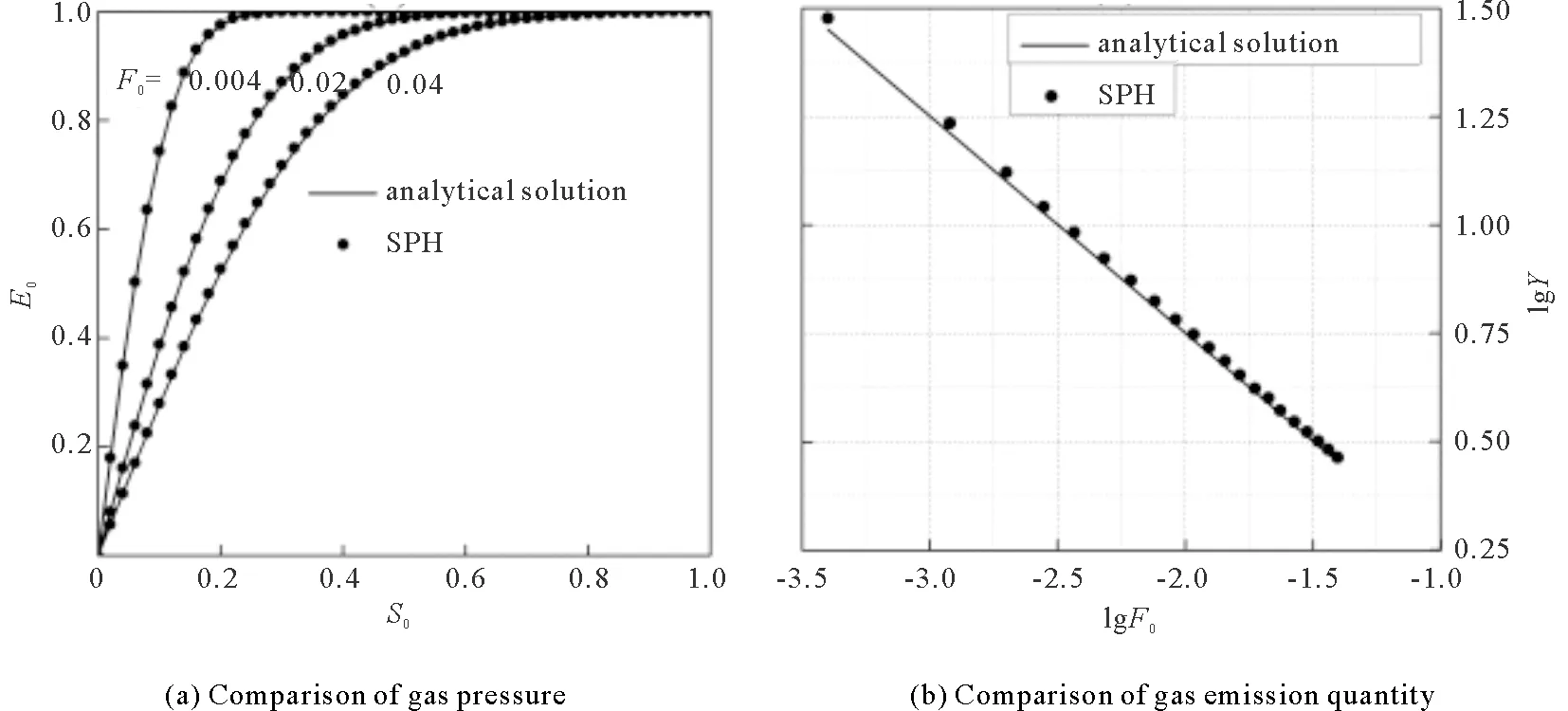
Fig.3 Analytical solution and SPH solution in different time periods

From Figure 3, it can be seen that for gas pressure, the SPH solution and analytical solution have sufficient accuracy. The gas emission quantity appears with little deviation between SPH solution and analytical solution because the gas pressure gradient is higher at the beginning of the SPH numerical simulation. Moreover, the SPH solution and analytical solution converge gradually with the extension of computing time. Therefore, SPH method can be a preferable way to simulate unsteady gas flow in infinite coal seam.

4 SPH numerical simulation of gas seepage in heterogeneous coal seam

The SPH simulation of gas flow in heterogeneous coal seam using gas seepage equation of variable coefficientφ(P) is carried out. Whenk=0, the model indicates heterogeneous condition along strike of coal seam, with valuesm=1/2,λ0=1,x0=4.

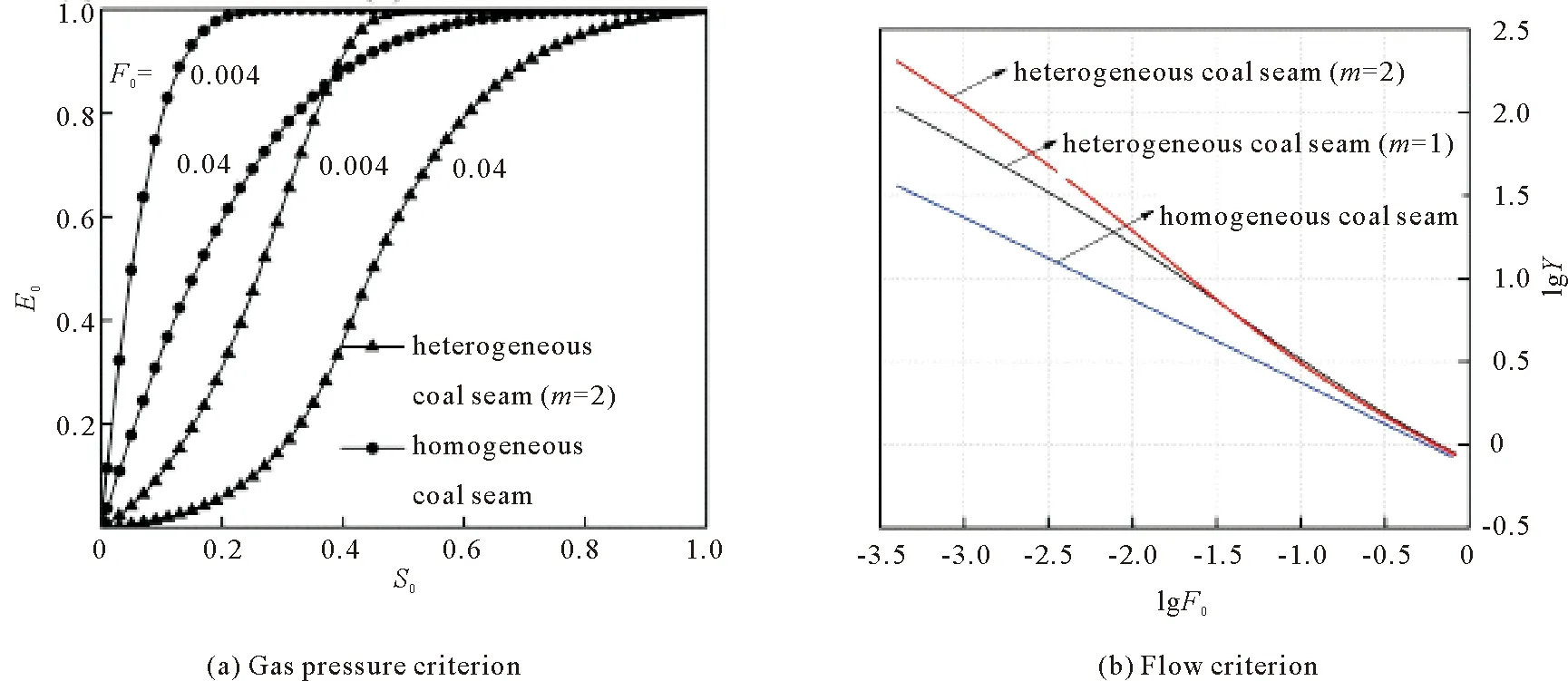
Fig.4 The distinctive curves of gas pressure criterion and flow criterion

From Figure 4(a), it can be seen that for heterogeneous condition along strike of coal seam, the gas pressure decreases rapidly and the pressure gradient near the coal wall is much lower as compared with homogeneous coal seam. From Figure 4(b), it can be found that the gas emission quantity shows linear distribution in homogeneous coal seam. In heterogeneous conditions along strike of coal seam, gas emission in coal wall increases evidently, while later it gradually weakens and tends to be homogeneous coal seam along with extended exposure time. The greater the value of parameterm, the more obvious the nonlinearity of gas flow will be.

Whilem=0 andk=1, the model indicates heterogeneous condition of Weibull distribution, by taking valuesn=2/10,λ0=1, and fork=1,λ0=1,m=1/2,x0=4,n=2/10 in the actual heterogeneous coal seam. The nephogram of permeability coefficient assigned by Weibull distribution is shown in Figure 5. The permeability coefficient in actual heterogeneous coal seam is shown in Figure 6.

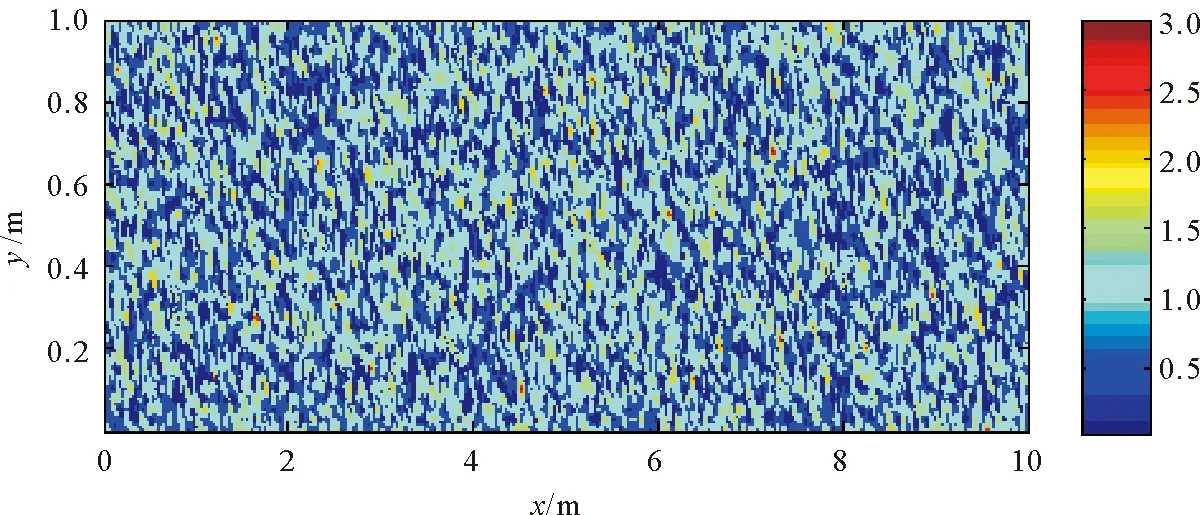
Fig.5 Permeability coefficient assigned by Weibull random distribution (n=2)

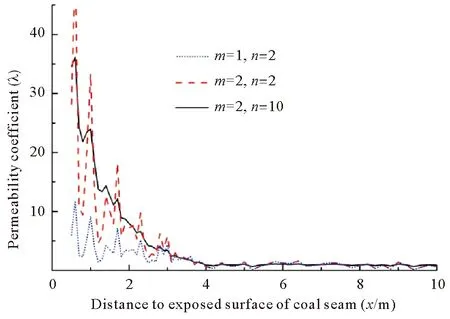
Fig.6 Permeability coefficient of section y=5 m

Flow criterions in heterogeneous condition of Weibull distribution and actual heterogeneous coal seam are shown in Figure 7 and Figure 8.

In homogeneous coal seam, the size and direction of gas flow are similar in the samexsection and there is no gas flow in theydirection. When permeability coefficient is assigned by Weibull distribution, the gas flow appears with fluctuations in size along strike of coal seam, and the fluctuation of size and direction appeared in the direction of the thickness of coal seam. Besides, for smaller values ofn, there will be more deviation in gas flow, compared with that of homogeneous coal seam. With this, the nonlinear flow characteristics can be shown obviously, as shown in Figure 7. The gap of gas flow inxandydirection is not evident when value of heterogeneous degreenis the same whilemis not. Whenmis the same, thenis smaller, and the average difference of gas emission quantity in thexandydirection is higher, as shown in Figure 8.

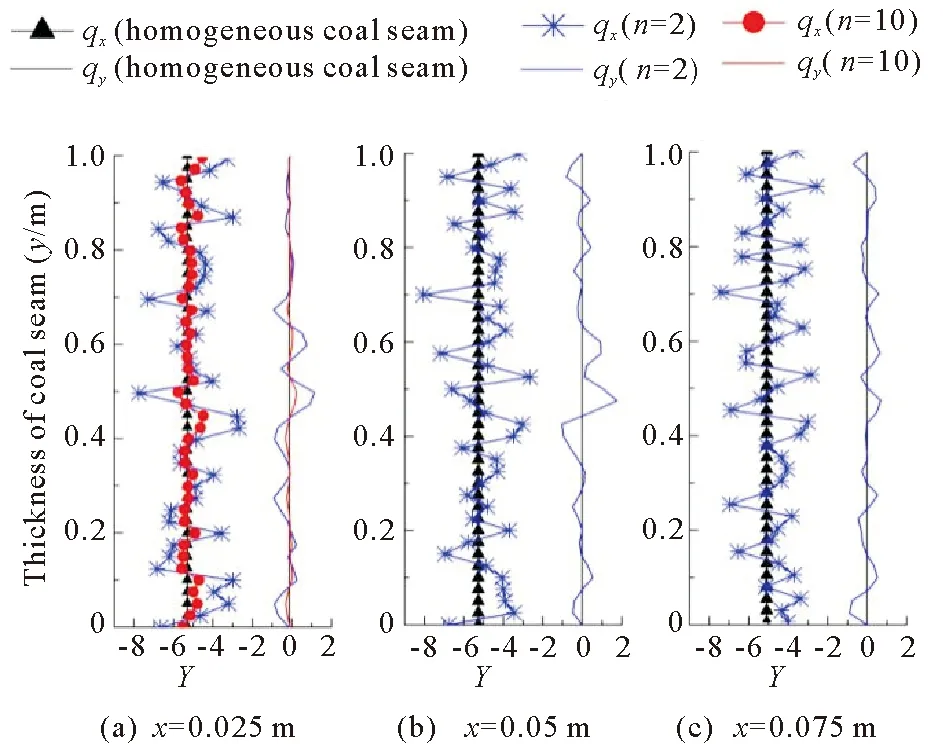
Fig.7 Flow criterions in heterogeneous coal seam andhomogeneous coal seam when F0=0.02

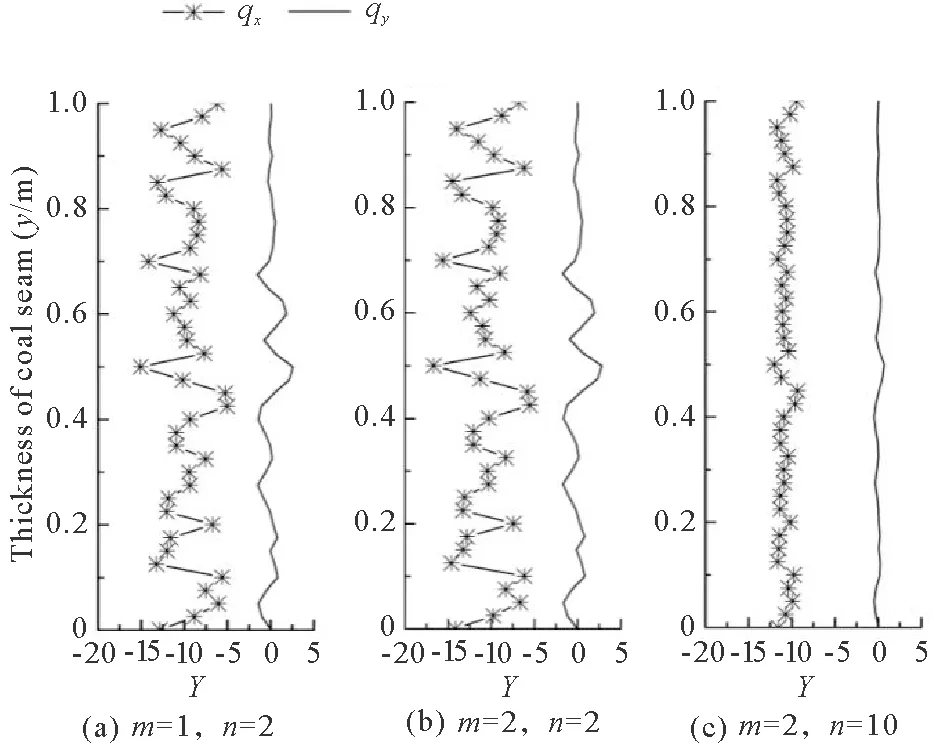
Fig.8 Flow criterions in seam thickness direction alongsection of x=0.025 m when F0=0.02

In order to illustrate the nonlinear characteristic of gas pressure in heterogeneous coal seam, letδ1=(Pxw-Pxh)/Pxh×100%,δ2=(Pxa-Pxs)/Pxs×100%, wherePxwis the gas pressure at locationxin heterogeneous condition of Weibull distribution,Pxhis the gas pressure at locationxin homogeneous coal seam,Pxais the gas pressure at locationxin actual heterogeneous coal seam,Pxsis the gas pressure at locationxin heterogeneous condition along strike of coal seam. As shown in Figure 9, gas pressure in the direction of seam thickness is no longer equal but produces a gradient in the heterogeneous condition of Weibull distribution. The smaller the value ofn, the more deviation there will be in the gas pressure as compared with that in homogeneous coal seam. Similarly, with the increase ofx, the average value ofδ1increases. This shows that the Weibull distribution weakens the permeability in the deep seam, and this weakening increases with the decrease ofn. There is a position of the relatively large gas pressure in Figure 9. It is evident that the large deviations of permeability coefficient of surrounding particles in the position makes the gas flow slower and leads to the smaller changes in the gas pressure. Due to higher gas pressure, this position may induce violent gas bursting, rock bursting and other similar disasters. As shown in Figure 10, pressure gradient in direction ofyin actual coal seam can be obtained. For smaller values ofnthere will be more deviation in the gas pressure, compared with the heterogeneous condition along strike of coal seam.

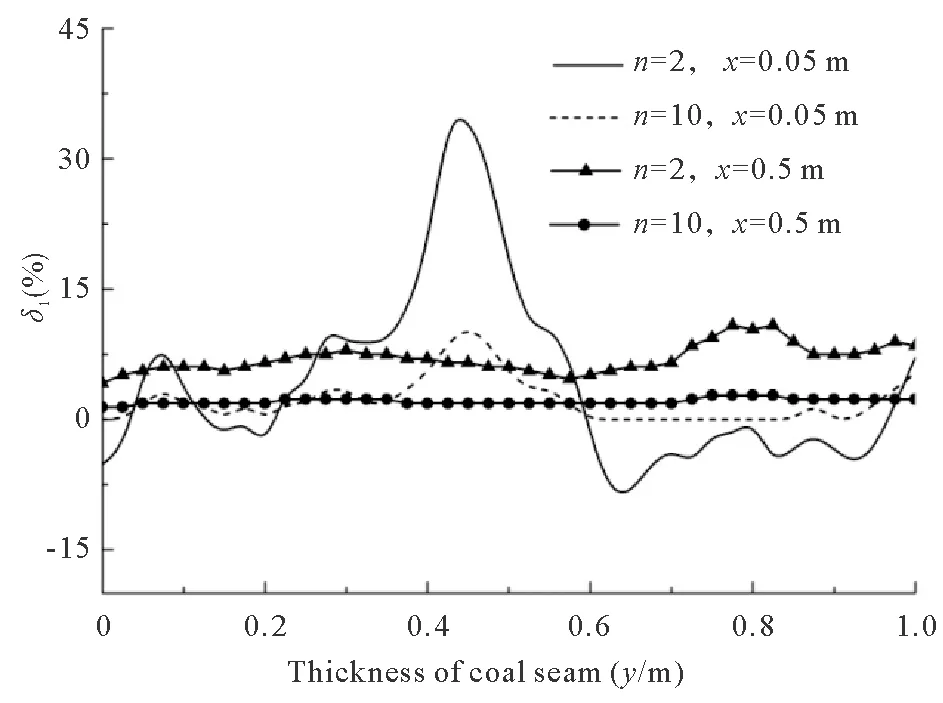
Fig.9 The change of δ1 in heterogeneous conditionof Weibull distribution when F0=0.02

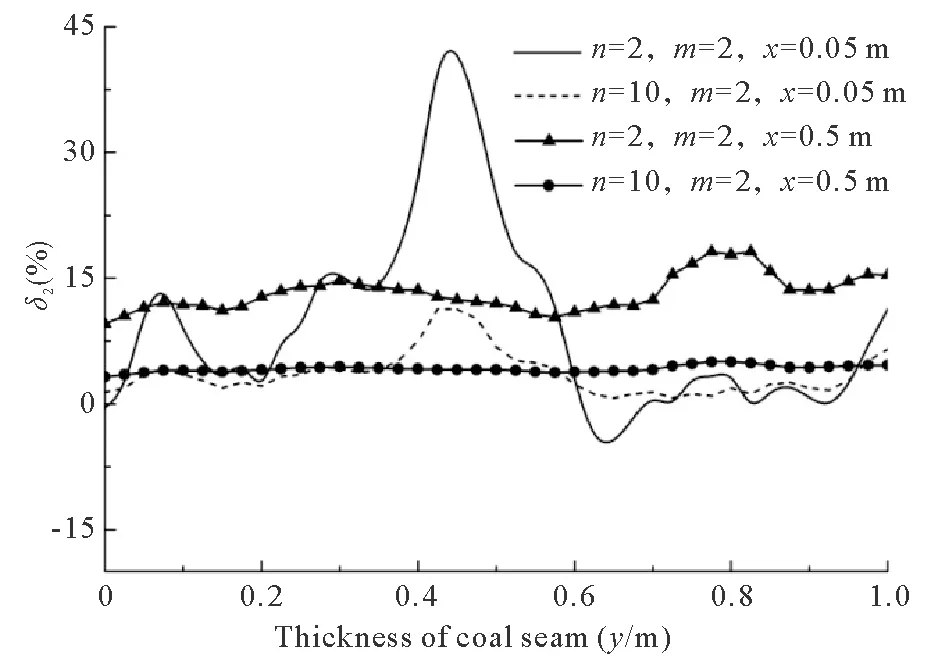
Fig.10 The change of δ2 in actual heterogeneouscoal seam when F0=0.02

In this paper, three kinds of typical heterogeneities are considered. The paper presents how the heterogeneity of coal causes nonlinear flow of gas. In addition, the characteristics of gas adsorption and desorption, the gas-liquid-solid coupling effect in coal seam are all likely to cause different gas flow in coal seam compared with linear flow.

5 Conclusions

1) We have verified that SPH solution has sufficient accuracy to simulate gas seepage. Simulation of gas flow in heterogeneous coal seam has been carried out by changing the permeability coefficient of coal seam.

2) It is found that the nonlinearity strength of gas flow is different when differentmvalues andnvalues are considered.

3) Even though the gas seepage equation has been established based on Darcy’s law, the gas flow still presents strong nonlinear characteristics considering the heterogeneous characteristics of coal seam.

4) The SPH method provides a novel and effective method for further study of gas seepage principles in heterogeneous coal medium.

[1]ZHOU S N,LIN B Q.The theory of gas flow and storage in coal seams[M].Beijing:China Coal Industry Publishing House,2009.

[2]HU G Z,WANG H T,TAN H X,et al.Gas seepage equation of deep mined coal seams and its application[J].Journal of China University of Mining and Technology,2008,18(4):483-487.

[3]TAN Y L,TENG G R,ZHANG Z A.Modified LBM model for simulating gas seepage in fissured coal considering Klinkenberg effects and adsorbability-desorbability[J].Chinese Physics Letters,2010,27(1):14-20.

[4]OSIPOV S N,PYASETSKII B P.Gas movement near exposed surface of a coal stratum with variable gas permeability[J].Fluid Dynamics,1966,1(3):96-100.

[5]FENG Z C,ZHAO D,ZHAO Y S,et al.Effects of temperature and pressure on gas desorption in coal in an enclosed system:A theoretical and experimental study[J].International Journal of Oil,Gas and Coal Technology,2016,11(2):56-74

[6]WANG J G,AKIM K,LIU J S.Effects of non-Darcy flow on the performance of coal seam gas wells[J].International Journal of Coal Geology,2012,93(6):62-74.

[7]SUN P D.Study on the law of gas flow in coal seam[J].Coal Journal,1987,4(7):74-82.

[8]CONNELL L D.Coupled flow and geomechanical processes during gas production from coal seams[J].International Journal of Coal Geology,2009,79(6):18-28.

[9]ZHANG C H,ZHAO Q S,YU Y J.Model of coupled gas flow and deformation process in heterogeneous coal seams and its application[J].Journal of Coal Science and Engineering,2011,17(1):76-80.

[10]CHENG G Q,ZHAO F,SHANG Y H,et al.Simulation of gas seepage in heterogeneous coal seam by SPH method[J].Journal of China Coal Society,2016,41(5):1152-1158.

[11]ZENG T F.Program realization and numerical simulation of gas seepage in heterogeneous coal seam by SPH method[D].Qingdao:Shandong University of Science and Technology,2012(in chinese).

[12]LIU G R,LIU M B.Smoothed particle hydrodynamics:A mesh free particle method[M].Singapore:World Scientific Publishing,2003.

[13]MONAGHAN J J,KOCHARYAN A.SPH simulation of multi-phase flow[J].Computer Physics Communications,1995,87(1):225-235.

[14]MONAGHAN J J.Implicit SPH drag and dusty gas dynamics[J].Journal of Computational Physics,1997,110(2):399-406.

[15]MONAGHAN J J,KAJTAR J B.SPH particle boundary forces for arbitrary boundaries[J].Computer Physics Communications,2009,180(10):1811-1820.

[16]SHEN H T,SU S J,LIU L W.SPH simulation of river ice dynamics[J].Journal of Computational Physics,2000,165(2):752-770.

(责任编辑：吕海亮)

SPHMethodforGasSeepageSimulationinHeterogeneousCoalSeam

CHENG Guoqiang, ZHAO Fang, MING Dezhi, TAN Yunliang

(College of Mining and Safety Engineering, Shandong University of Science and Technology, Qingdao, Shandong 266590, China)

TD712

A

1672-3767(2017)06-0052-08

10.16452/j.cnki.sdkjzk.2017.06.008

2016-12-29

国家自然科学基金项目(51274133,51474137);瓦斯灾害监控与应急技术国家重点实验室开放课题(2012CQCCTEG04KF01)

程国强(1969—)，男，山西翼城人，教授，博士，主要从事岩石计算力学科研与教学工作. E-mail: sdnslab@163.com