The number of solutions of generalized Markoff-Hurwitz-type equations over finite fields

2017-10-10 01:02HUShuangnianLIYanyan

浙江大学学报（理学版） 2017年5期

HU Shuangnian, LI Yanyan

(1. School of Mathematics and Statistics, Nanyang Institute of Technology, Nanyang 473004, Henan Province, China;2. School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, China; 3. School of Electronicand Electrical Engineering, Nanyang Institute of Technology, Nanyang 473004, Henan Province, China)

HU Shuangnian1,2, LI Yanyan3

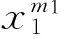
finite field; rational point; Markoff-Hurwitz-type equations

0 Introduction and the main result

Markoff-Hurwitz-type equations are the following type of the Diophantine equation:

wheren,care positive integers andn≥3. This type of equations were firstly studied by MARKOFF[1]for the casen=3,c=3 because of its relation to Diophantine approximation. More generally, these equations were studied by HURWITZ[2].

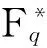
Recently, BAOULINA[5-7]studied the generalized Markoff-Hurwitz-type equation:

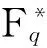
(1)

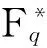
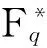
In this paper, we consider the rational points of the further generalized Markoff-Hurwitz-type equations of the form

(2)

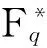
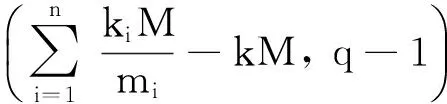
Nq=qt-1+(-1)n-1(q-1)t-n.

Clearly,Nqis independent of the coefficientsai,cand the exponentskn+1,…,kt. Lettingt=n, then theorem 1 reduces to the theorem of PAN et al[8]. Theorem 1 also generalizes the main results of [10] in some other cases.

This paper is organized as follows. In section 1, we recall some useful known lemmas. In section 2, we make use of the results presented in section 1 to show theorem 1. Some interesting applications of theorem 1 will be provided as corollaries at the end.

1 Preliminary lemmas

In this section, we present some useful lemmas which are needed in section 2. Letmbe a positive integer andh(x1,x2,…,xr) be a polynomial with integer coefficients. We useN[h≡0(modm)] to denote the number of the solutions of the congruenceh(x1,x2,…,xr)≡(modm). We first recall two well known results in the elementary number theory.

Lemma1[13]Leta,bbe positive integers. Then

gcd(a,b)lcm[a,b]=ab.

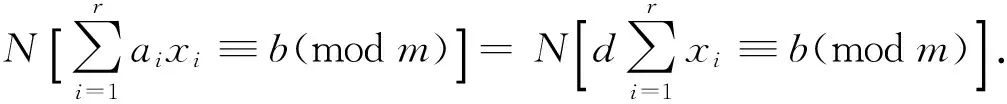
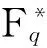
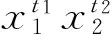
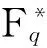
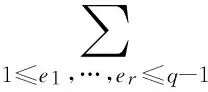
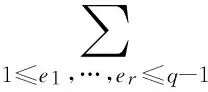
Nq[a(x1x2…xr)d=α].

Since lemma 2 tells us that

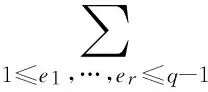
Then the desired result follows immediately. This ends the proof of lemma 2.

The following result comes from PAN et al[8].

Nq[a1x1m1+a2x2m2+…+anxnmn=cx1k1x2k2…xnkn]=

qn-1+(-1)n-1.

2 Proof of theorem 1

In this section, we give the proof of theorem 1.

ProofFirstly, we claim that the condition of lemma 5 is equivalent to the conditions of theorem 1. That is, the condition

is equivalent to the following two conditions:

are pairwise coprime. Since

thus we can deduce that the condition

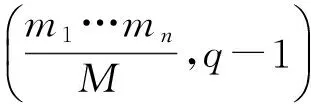
(3)

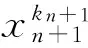
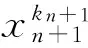
qt-n-(q-1)t-n.

(4)

Using the assumptiond1,d2,…,dnare pairwise coprime, it follows from (4) and lemma 4 that

(qt-n-(q-1)t-n)×

qn-1(qt-n-(q-1)t-n)=

qt-1-qn-1(q-1)t-n.

(5)

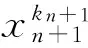
d(q-1)t-n-1×

(6)

Then, it follows from lemma 6 that

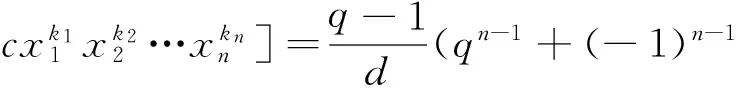
(7)

Using (6) and (7), one can derive that

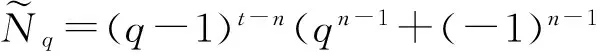
(8)The desired result can follow immediately from (3),(5) and (8). This ends the proof of theorem 1.

In concluding this section, we present some trivial corollaries.

Corollary1For the further generalized Markoff-Hurwitz-type equations of the form

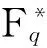
Nq=qt-1+(-1)n-1(q-1)t-n.

Corollary2For the further generalized Markoff-Hurwitz-type equations of the form

(a1x1m1+a2x2m2+…+anxnmn)k=cx1m1x2m2…xtmt

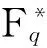
Nq=qt-1+(-1)n-1(q-1)t-n.

Corollary3For the further generalized Markoff-Hurwitz-type equations of the form

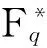
Nq=qt-1+(-1)n-1(q-1)t-n.

Clearly, corollaries 1～3 are some special cases of theorem 1. For example, consider the further generalized Markoff-Hurwitz-type equation over

(8)

[1]MARKOFFAA.Surlesformesquadratiquesbinairesindéfinies[J].MathematischeAnnalen,1880,17(3):379-399.

[2] HURWITZ A. Über eine aufgabe der unbestimmten analysis[J].ArchivderMathematikundPhysik,1907(3):185-196.

[3] CARLITZ L. Certain special equations in a finite field[J].MonatshefteFürMathematik,1954,58(1):5-12.

[4] CARLITZ L. The number of solutions of some equations in a finite field[J].PortugaliaeMathematica,1954,13(1):25-31.

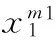
[6] BAOULINA I. Generalizations of the Markoff-Hurwitz equations over finite fields [J].JournalofNumberTheory,2006,118(1):31-52.

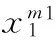
[8] PAN X L, ZHAO X R, CAO W. A problem of Carlitz and its generalizations[J].ArchivderMathematik,2014,102(4):337-343.

[9] CAO W. On generalized Markoff-Hurwitz-type equations over finite fields [J].ActaApplicandaeMathematicae,2010,112(3):275-281.

[10] SONG J, CHEN F Y. The number of some equations over finite fields[J].JournalofUniversityofChineseAcademyofSciences,2015,32(5):582-587.

[11] CAO W, SUN Q. On a class of equations with special degrees over finite fields [J].ActaArithmetica,2007,130(2):195-202.

[12] ZHAO Z J, CAO X W. On the number of solutions of certain equations over finite fields [J].JournalofMathematicalResearchandExposition,2010,30(6):957-966.

[13] KENG H L.IntroductiontoNumberTheory[M]. Heidelberg: Springer-Verlag,1982.

[14] BAOULINA I. Solutions of equations over finite fields: Enumeration via bijections [J].JournalofAlgebraandItsApplications,2016,15(7):1650136.

[15] LIDL R, NIEDERREITER H.FiniteFields-EncyclopediaofMathematicsandItsApplications[M]. 2nd ed. Cambridge: Cambridge University Press,1997.

胡双年1,2，李艳艳3

(1. 南阳理工学院数学与统计学院，河南南阳 473004； 2. 郑州大学数学与统计学院，河南郑州 450001； 3. 南阳理工学院电子与电气工程学院，河南南阳 473004)

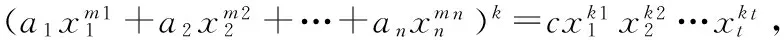
有限域；有理点；Markoff-Hurwitz-type方程

O 156.1

：A

：1008-9497(2017)05-516-04

date：Nov.7, 2016.

Supported by the Key Program of Universities of Henan Province of China (17A110010), China Postdoctoral Science Foundation Funded Project (2016M602251) and by the National Science Foundation of China Grant (11501387).

Abouttheauthor:HU Shuangnian (1982-),ORCID:http://orcid.org/0000-0002-5174-8460,male, Ph.D, lecturer, the field of interest is number theory, E-mail:hushuangnian@163.com.

10.3785/j.issn.1008-9497.2017.05.003

有限域上广义Markoff-Hurwitz-type方程的有理点个数.浙江大学学报(理学版),2017,44(5):516-519,537