扭转索面斜拉桥索力调整

李才，陈婷婷

(山东省交通科学研究院，山东 济南 250031)

扭转索面斜拉桥索力调整

李才，陈婷婷

(山东省交通科学研究院，山东 济南 250031)

为研究较为合理的扭转索面斜拉桥索力调整的方法，结合工程实践，阐述索力调整的目标和原则，利用影响矩阵法和桥梁结构有限元分析软件Midas Civil 2012，采用试算法制定调索方案，并对调索效果进行分析。监测结果表明：索力调整后，全桥索力接近目标值，主梁线形和塔偏也比较理想。

斜拉桥；索力调整；扭转索面；影响矩阵；Midas

斜拉桥具有优越的结构受力体系和美丽的外形，主要由主塔、拉索和主梁组成[1-4]。斜拉桥索力调整一直是研究的热点，一座斜拉桥包含很多拉索，一根索索力的变化会影响到其他索，因此调整斜拉桥索力时要全桥考虑[5-7]。斜拉桥索力调整的计算方法主要有影响矩阵法、逼近法、数学规划法等，这些方法具有各自的特点和适用性，在实际应用中要根据具体的桥梁和试验反复调整[8-9]。扭转索面是指斜拉索在空间上呈扭转曲面布置，最长的斜拉索在塔上的锚点位置最低，而最短的拉索在塔上的锚点位置最高，最长拉索与桥面的夹角仅为23.4°。本文结合钢箱梁扭转索面斜拉桥索力调整实践，阐述索力调整的目标和原则，利用影响矩阵法和桥梁结构有限元分析软件Midas Civil 2012，采用试算法制定调索方案，对调索过程进行监测，并对调索效果进行分析。

1 工程概况

天津蓟运河大桥为两跨布置的空间扭转索面独塔斜拉桥，主梁为扁平式钢箱梁。跨境布置为2×118 m ，桥梁全长为236 m。主桥结构采用半飘结构体系，主塔与主墩固结，桥塔全高91.5 m，主塔由钢塔和混凝土塔2部分组成，具体分为塔顶、钢塔、钢混结合段塔、混凝土塔4部分，基础均为钻孔灌注桩基础。全桥共设4×13 根斜拉索。斜拉索一侧锚固在塔上，一侧锚固在钢箱梁外侧腹板。斜拉索顺桥向间距7 m，水平索距由主塔中心起向两端桥台为(23+12×7+11)m，主塔一侧无索区长度为23 m，边墩无索区长度为11 m。斜拉索上锚固端位于钢塔两侧箱室腹板上，竖向索距2.5 m。设计汽车荷载为城市-A，人群荷载3.5 kPa。蓟运河大桥立面布置如图1所示。

2015-01-06，全桥拉索张拉完成后发现桥面标高没有达到预期值，索力动测仪测量结果显示全桥索力均未达到预期值，这是由于摩阻力使张拉千斤顶油表读数不准，导致张拉力不足。为使索力和桥面标高达到预期值，需要进行索力调整。第一次张拉完成后的索力与预期值对比见表1。

2 索力调整

2.1目标和原则

索力不足是全桥桥面标高达不到预期值的根本原因。对于斜拉桥，可以通过调整索力改变全桥拉索的受力状态和桥面线型，使桥梁结构达到最佳受力状态和线型更接近设计线型[10]。本次调索的目标为：调索后全桥索力相对于目标索力的差值在±5%内，桥面标高与预期值的偏差在±20 mm内。

图1 蓟运河大桥立面布置图

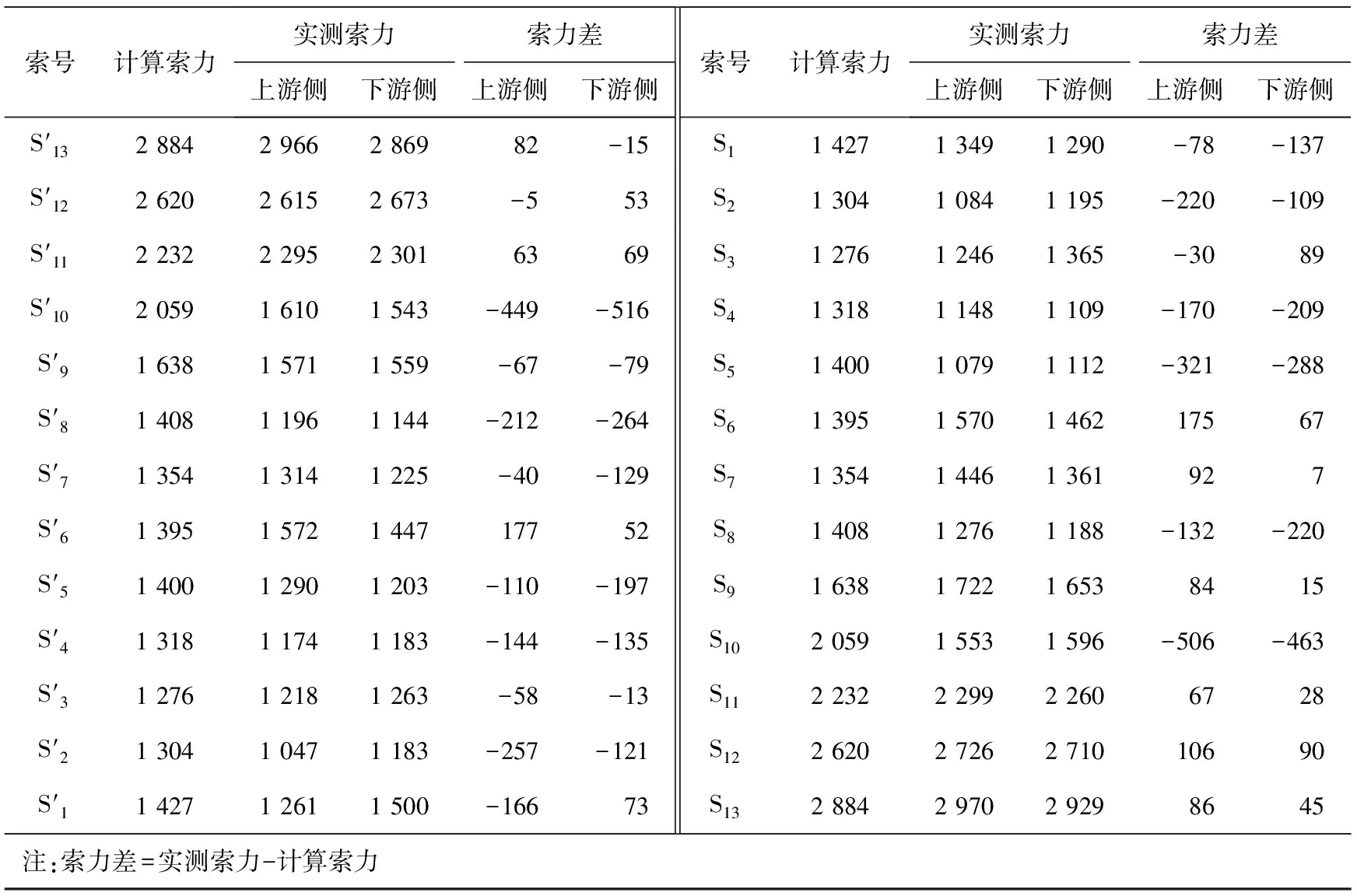
表1 第一次张拉完成后的索力 kN

索力调整应兼顾主梁线型、主梁应力以及塔偏的变化[11-12]。第一次张拉完成后，桥面标高整体较预期值低很多，因此，调索后应使桥面整体升高，并避免主梁线型产生较大变化，以免主梁应力过大。

2.2索力调整难点

扭转索面与平面索面不仅在形式上大不相同，结构受力也更为复杂，调整索力时主要难点有：1)扭转索面拉索长度差别较大，拉索越长索力越大。2)长拉索与桥面夹角较小，索力变化时对主梁内力影响较大，调索时需兼顾主梁内力。3)一根索力调整对全桥索力影响很大，计算索力时需要反复迭代计算，直至闭合。

2.3索力调整方案

调索计算采用桥梁结构有限元分析软件Midas Civil 2012。主塔和主梁采用梁单元模拟，拉索采用索单元模拟，全桥共划分73个梁单元、52个索单元，计算模型如图2所示。

图2 计算模型

计算时首先采用影响矩阵法分析相邻拉索之间的相互影响程度[13-14]，分别计算每组拉索张拉100 kN的全桥索力，分析调索对其他拉索的影响程度。分析结果表明：索力调整仅对该索号前后各3对拉索的索力影响明显，对其余索的影响可忽略不计。以第一次张拉完成后的索力为原始状态，利用Midas Civil 2012结合迭代计算制定出调索顺序和调整值[15-16]。迭代计算的步骤为：1)将1#拉索实测索力与目标索力差值的一半施加到相应拉索上，分析全桥索力的变化，然后以相同的方法依次调整2#～13#拉索；2)重复步骤1)直至全桥索力达到目标值；3)每根拉索的累积调整量即为调索时的索力调整值。

调索过程中对索力、桥面标高和塔偏进行监控，调索过程中的索力监测采用索力动测仪[17-19]，每调整完一组索力，比较实测值和计算值及其偏差，如偏差太大，应分析原因及时调整调索方案。调索时，相同编号的4根索同时对称张拉。根据计算结果制定调索步骤如表2。

表2 索力调整步骤

2.4调索效果分析

调索过程中分别对索力变化、桥面高程变化和塔偏进行监测，并将实测变化量和计算变化量进行对比分析，结果表明索力桥面高程和塔偏的变化规律均与预期相吻合。现将调索前后全桥结构状态的变化进行对比分析。

1)全桥索力

调索完成后将实测索力与计算索力进行对比，见图3。结果表明索力与计算值吻合较好，偏差均在±5%以内。

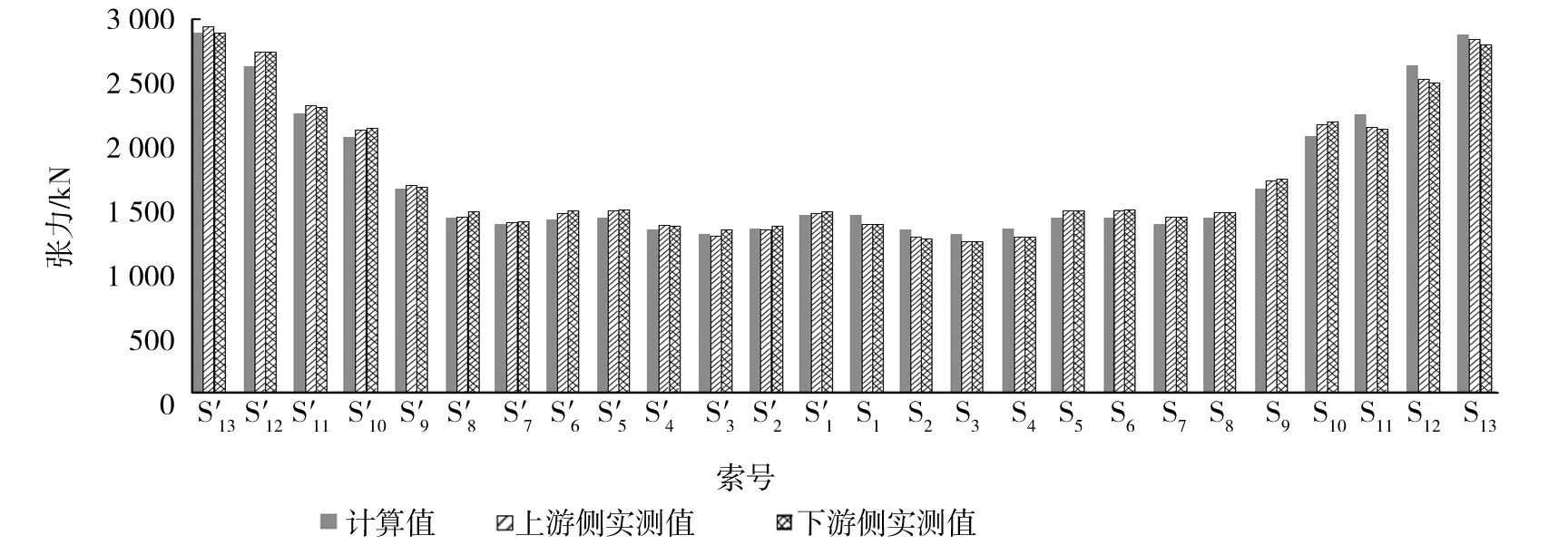
图3 调索后索力实测值与计算值对比表

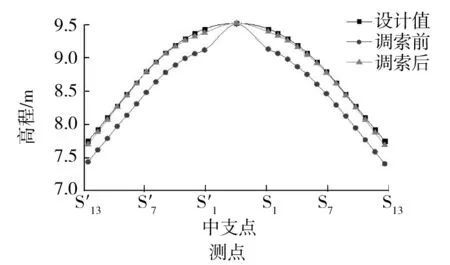
图4 调索前后桥面线形的变化

2)桥面线形

调索后，桥面线形的变化如图4所示。从图4可以看出，桥梁线形和预期值吻合较好，使主梁的受力更趋合理，调索后桥面总体升高了，最大抬高量为92 mm，在S7的下游侧。

3)塔顶偏位

调索前，即第一次张拉完成后，塔顶偏位为纵桥向28 mm，横桥向无偏位。调索完成后，纵桥向为-14 mm，横桥向右偏13 mm。调索使得塔偏有所缓解。

3 结论

1)对于主梁为钢箱梁的扭转索面斜拉桥，采用桥梁结构有限元分析软件结合迭代法计算索力调整值是可行的。

2)由于摩阻力的存在，用张拉千斤顶的油表读数控制索力是不可靠的，特别是对倾斜度较大的拉索。

3)本文采用的索力调整方法和工程实践为斜拉桥的索力调整积累了经验，可作为类似工程的参考。更加精准的索力检测技术还有待研究。

[1]蒋伟平.斜拉桥换索理论及其技术问题的研究[D].成都：西南交通大学，2000. JIANG Weiping. Research on cable-changing theory and technical problems of cable-stayed bridge[D].Chengdu: Southwest Jiaotong University，2000.

[2]VIRLOGEUX M. Recent evolution of cable-stayed bridges[J]. Engineering Structures，1999，12(8):737-755.

[3]贾丽君，肖汝诚，孙斌，等.确定斜拉桥施工张拉力的影响矩阵法[J].苏州城建环保学院学报，2000，13(4)：17-21. JIA Lijun，XIAO Rucheng，SUN Bin，et al. Influence matrix method for determining tensile force of cable-stayed bridge[J]. Journal of Suzhou Urban Construction Environmental Protection College，1999，12(8):737-755.

[4]严国敏.现代斜拉桥[M].成都:西南交通大学出版社，1989.

[5]肖汝诚，项海帆.斜拉桥索力优化的影响矩阵法[J].同济大学学报，1998，26(3)：235-240. XIAO Rucheng，XIANG Haifan. Influence matrix method for cable force optimization of cable-stayed bridge[J]. Journal of Tongji University，1998，26(3)：235-240.

[6]杜蓬娟，张哲，刘春城，等.斜拉桥索力张拉过程的最优控制[J].计算力学学报，2005，22(3)：326-329. DU Pengjuan，ZHANG Zhe，LIU Chuncheng，et al. Optimal control of cable tensioning process of cable-stayed bridge[J]. Chinese Journal of Computational Mechanics，2005，22(3)：326-329.

[7]官万轶，韩大建.斜拉桥的索力调整[J].昆明理工大学学报，2000，25(1)：125-128. GUAN Wanyi，HAN Dajian. Cable tension adjustment of cable-stayed bridge[J]. Journal of Kunming University of Technology，2000，25(1)：125-128.

[8]王美.红枫湖大桥成桥后索力调整及其调索顺序的优化[D].大连：大连理工大学，2005. WANG Mei. Adjustment of cable force and optimization of tuning order of Hongfeng Lake Bridge[D].Dalian：Dalian University of Technology，2005.

[9]方志，汪建群，颜江平.基于频率法的拉索及吊杆张力测试[J].振动与冲击，2007，26(9):78-82. FANG Zhi，WANG Jianqun，YAN Jiangping. Tension test of cable and boom based on frequency method[J]. Vibration and Shock，2007，26(9):78-82.

[10]PODOLNY J W J，SCALZI J. Construction and design of cabled-stayed bridge[M]. New York: John Wiley & Sons，1986.

[11]林元培.斜拉桥[M].北京:人民交通出版社，1994.

[12]许立强.确定斜拉桥合理成桥索力的综合方法与施工控制研究[D].武汉:武汉理工大学，2007. XU Liqiang. Study on comprehensive method and construction control of cable-stayed bridge[D].Wuhan: Wuhan University of Technology，2007.

[13]金增洪.斜拉桥的历史和美学(上)[J].国外公路，1997，17(2):21-26. JIN Zenghong. The history and aesthetics of cable-stayed bridge(I)[J]. Foreign Highway，1997，17(2):21-26.

[14]金增洪.斜拉桥的历史和美学(下)[J].国外公路，1997，17(3):26-32. JIN Zenghong. The history and aesthetics of cable-stayed bridge(II)[J]. Foreign Highway，1997，17(3):26-32.

[15]蔡国宏.斜拉桥的发展经验和展望[J].国外公路，1997，17(4):19-24. CAI Guohong. Development experience and prospect of cable-stayed bridge[J]. Foreign Highway，1997，17(4):19-24.

[16]TANG M C. Cable-stayed bridges in North America[J]. Cable-Stayed Bridge，1991，17(2):14-17.

[17]TANG M C. International symposiumon on cable-stayed bridges[C]. Shanghai:[s.n.]，1994.

[18]刘士林，梁智涛，侯金龙，等.斜拉桥[M].北京:人民交通出版社，2002.

[19]铁道部大桥工程局桥梁科学研究所.斜拉桥[M].北京:科学技术文献出版社，1992.

CableForceAdjustmentofCable-StayedBridgewithTwistingCablePlane

LICai,CHENTingting

(ShandongScientificResearchInstituteofTransportation,Jinan250031,China)

In order to explore the reasonable method to adjust the cable force of the cable-stayed bridge with the twisting cable plane, the objectives and principles of the cable tension adjustment combining with engineering practice is discussed. The influence matrix method, the finite element analysis software of bridge structure, Midas Civil 2012 and a trial method are used to design the scheme and analyze the effect of the adjustment. The monitoring results show that the cable force of the bridge is close to the target value after the adjustment of the cable force, and the bridge line and tower are also ideal.

cable-stayed bridge; cable force adjustment; twisting cable plane; influence matrix; Midas

U448.27

：A

：1672-0032(2017)03-0057-05

(责任编辑：郎伟锋)

2016-12-11

李才(1986—)，男，山东菏泽人，工学硕士，助理工程师，主要研究方向为桥梁，382994631@qq.com.

10.3969/j.issn.1672-0032.2017.03.009