遗传与粒子群算法在闭环混合系统运作中的应用
王心月 郭健全

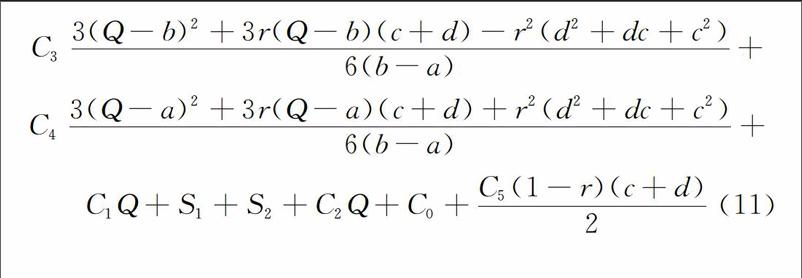

摘 要:设计需求和再制造率不确定情况下的制造/再制造系统的最优回收及生产策略模型,并通过具体算例,采用遗传算法(GA)和粒子群算法(PSO)求解,对比验证模型的信度和效度。仿真结果表明,两种算法既可灵活获得多种情况下的系统最优运作策略,又能反映制造数量和回收品质量水平在不同再制造率下的变化规律,可为企业在多重不确定下降低总成本提供参考。
关键词:随机需求;随机再制造率;闭环混合系统;GA&PSO
DOI:10.11907/rjdk.172073
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2017)009-0034-04
Abstract:The optimal recycling and production strategy model based on random demand and yield is investigated in a closed-loop hybrid manufacturing/remanufacturing system. A numerical example is used to verify the validity and credibility of the model by adopting genetic algorithm (GA) and particle swarm optimization (PSO) algorithm. The results show that it is applicable for GA and PSO to solve the optimal operation strategy according to different situations and the variations of manufacturing quantity and the quality level of the returned items under the different remanufacturing rate are presented. A reference could be provided for minimizing the total cost of the system in view of multiple uncertainties.
Key Words:random demand; random yield; closed-loop hybrid system; GA&PSO
0 引言
近年來环境问题日益突出,再制造成为节能减排和提高资源利用率的有效方式[1]。再制造作为闭环供应链的重要组成部分,其回收品的数量、市场需求和再制造率等一系列未知因素加大了生产计划的难度[2]。Han等[3]提出优化模型解决不确定需求下的混合制造/再制造定价问题,并对不确定参数进行敏感性分析。Shi等[4]假设需求和回收存在不确定性,建立利润最大化模型来研究供应链的生产计划。Pokharel和Liang[5]研究回收品被随机用于再制造的最优回收定价及回收数量问题。以上研究较少考虑再制造率的随机性,以及未能在多重不确定环境下研究回收与生产决策。
在再制造生产计划问题中,较多采用遗传算法、蚁群算法、模拟退火、粒子群算法等单一智能算法,虽然其效果显著,但每种算法都有各自的局限性。鉴于此,区别于以往单一算法的局限性,在多重不确定下的闭环混合制造/再制造系统最优回收及生产计划中,采用粒子群和遗传两种算法,对具体实例对比验证求解,既避免粒子群算法陷入局部最优,又避免遗传算法搜索速度的局限性,更具有可靠性和互补性。
1 数学规划模型
混合制造/再制造系统如图1所示,包含制造品和再制造品组成的可用库存、回收品库存及原材料库存3部分。制造商回收旧产品,同时生产制造品和再制造品,且两种产品质量无差异,共同满足市场需求。
1.1 模型假设
作如下假设:①回收品质量水平服从指数分布[6];②回收成本、再制造成本是关于回收品质量水平的负指数函数[7];③再制造品和新产品质量无差异[8];④不考虑提前期[9];⑤需求服从均匀分布,M∈(a,b),b>a,a>0;回收品数量服从均匀分布,N∈(c,d),d>c,c>0[10]。
1.2 函数构建
1.2.1 回收成本函数
定义回收品最佳质量水平为q(0≤q≤1),q服从指数分布,q~E(λ), x为回收品质量水平(q≤x≤1),λ为指数分布参数。其概率密度函数为X(x)=λe—λx,q 0,其它。 其中,w为惯性权重,其影响上次迭代过程中粒子在此次迭代过程中速度的大小。c1、c2为加速度常数,c1代表粒子自身的认知学习能力,是粒子对比自身最优适应度值的惯性权重系数。c2代表整个粒子群体认知的能力,是粒子参照种群最优适应度值的惯性权重数。r1、r2是一组随机数,分布在[0,1]区间内。限定粒子的速度vin∈[-Vmaxn,Vmaxn],以免粒子在搜索过程中超出所定义的空间。 粒子群算法的主要编写步骤如下: 步骤1:设定粒子群规模为N,随机初始化粒子位置及速度信息,本文初始化回收品质量水平q,再制造率r和制造数量Q。 步骤2:根据适应度函数(11)获得所有粒子的适应度值大小。 步骤3:比较历史适应度值,若当前适应度值较优,则记为Pbest;比较群体最优适应度值,若当前适应度值较优,则记为gbest。 步骤4:根据进化方程(12)-(14)对粒子位置和速度持续更新。 步骤5:若满足终止规则,终止程序并输出最优解,否则转向步骤2。
2.2 遗传算法
遗传算法(GA)是一种模拟生物演化过程的智能搜索算法,具有鲁棒性、并行性等特点,被广泛用于求解复杂优化问题[12]。因此,本文同时选用遗传算法对比验证解决多目标优化问题。
遗传算法的主要步骤如下:
步骤1:初始化。随机产生由若干个个体组成的一个初始种群,如图2所示。
步骤2:适应度评估。适应度直接反映个体的优劣程度,个体适应度值用适应度函数f(x)=1 000/objvalue(11)来评估计算。
步骤3:选择。选择的目的是提高全局收敛性及效率,使适应度值较大的个体有机会成为父代,个体被选择的概率为p(x)=f(x)/∑f(x)。
步骤4:交叉与变异。交叉:使新一代继承父代的特性,并具有高于父代的适应性,从而保证全局搜索能力。一个交叉算子如图3所示。变异:以较小概率随机改变某个个体的基因值,形成的新个体保证了种群的多样性。
步骤5:终止条件。若到达预设的最大迭代次数,终止算法,否则转向步骤2。
3 模型求解
为验证模型和算法的有效性,采取具体实例验证。已知h1=0.2,h2=1,h3=0.2,C1=10,C2=5,C3=12,C4=4,C5=3,CO=800,S1=1 000,S2=1 000,a=1 000,b=1 300,c=200,d=850,l=0.9,k=0.9,γ=0.1,β=0.9,φ=2,λ=1。对于不同的θ(回收成本函數参数)和δ(再制造成本函数参数),PSO和GA分别求得的最优策略如表1所示,GAP值=(PSO-GA)/GA。以θ=4,δ=1为例,两种算法计算的不同再制造率下的最优回收及生产方案,如图4—图6所示。
表1表明:①两种算法都可求出最优解,即验证了模型的有效性;②两种算法的GAP值最大是0.003%,即表明解未陷入局部最优,进一步验证了模型的可信度;③当δ保持不变时,随着θ逐渐增大,Q逐渐增大,q逐渐减小,逐渐减小,ATC逐渐增大。即企业通过降低回收品最佳质量水平来尽可能降低回收成本,再制造率因回收品质量水平的下降而下降,进而制造数量因再制造数量的下降而升高;④当θ保持不变时,随着δ逐渐增大,Q逐渐增大,q逐渐增大,r逐渐增大,ATC逐渐增大。即企业通过提高回收品最佳质量水平来尽可能降低再制造成本,再制造率r也因回收品质量水平的上升而上升,进而制造数量因再制造数量的上升而下降;⑤PSO和GA计算结果与事实相符合,可以合理解释模型的经济意义,即验证了两种算法求解混合系统运作策略具有较高的应用价值。
由图4—图6可得到以下结论:①随着r逐渐增大,Q逐渐减小,q逐渐增大,即随着再制造率的上升,可用于再制造的回收品数量上升,因此制造品数量逐渐下降,回收品质量水平随着再制造率的上升呈现上升趋势;②由PSO和GA两种算法计算出的ATC变化趋势可看出,两种算法变化趋势一致,且结果差值较小,可见该模型可信度较高,同时也验证了两种算法解决该问题的合理性,更具有说服力。
4 结语
在不确定需求、不确定再制造率和不确定质量下建立闭环混合系统的最优回收及生产决策模型,并采用GA算法和PSO算法对比验证模型的可信性和有效性。实验表明,两种算法能规避单一算法的局限性,较好解决混合系统的生产计划问题。
参考文献:
[1] WANG Y, CHANG X, CHEN Z, et al. Impact of subsidy policies on recycling and remanufacturing using system dynamics methodology: a case of auto parts in China[J]. Journal of Cleaner Production,2014,74(7):161-171.
[2] WANG J, ZHAO J, WANG X. Optimum policy in hybrid manufacturing/remanufacturing system[J].Computers & Industrial Engineering,2011,60(3):411-419.
[3] HAN S, MA W, ZHAO L, et al. A robust optimisation model for hybrid remanufacturing and manufacturing systems under uncertain return quality and market demand[J].International Journal of Production Research,2016,54(17):5056-5072.
[4] SHI J, ZHANG G, SHA J. Optimal production and pricing policy for a closed loop system[J]. Resources, Conservation and Recycling,2011,55(6):639-647.
[5] POKHAREL S, LIANG Y. A model to evaluate acquisition price and quantity of used products for remanufacturing[J]. International Journal of Production Economics,2012,138(1):170-176.
[6] GUO J, YA G. Optimal strategies for manufacturing/remanufacturing system with the consideration of recycled products[J]. Computers & Industrial Engineering, 2015,89:226-234.endprint
[7] Vrs J. Product Balancing under conditions of quality inflation, cost pressures and growth strategies[J]. European Journal of Operational Research,2002,141(1):153-166.
[8] ARAS N, VERTER V, BOYACI T. Coordination and priority decisions in hybrid manufacturing/remanufacturing systems[J]. Production and Operations Management,2006,15(4):528-543.
[9] WANG X, GUO J, LIANG C. Optimal strategies for a closed-loop hybrid system with supply disruption in e-commerce environment[C]. 2016 IEEE 13th International Conference on e-Business Engineering (ICEBE),2016:299-304.
[10] GIRI B C, SHARMA S. Optimal production policy for a closed-loop hybrid system with uncertain demand and return under supply disruption[J]. Journal of Cleaner Production,2016,112:2015-2028.
[11] ORESKI S, ORESKI G. Genetic algorithm-based heuristic for feature selection in credit risk assessment[J].Expert systems with applications,2014,41(4):2052-2064.
[12] HAO J X, YU Y, LAW R, et al. A genetic algorithm-based learning approach to understand customer satisfaction with OTA websites[J]. Tourism Management,2015,48:231-241.
(責任编辑:孙 娟)endprint

