机动飞行器内碰摩转子的非线性动力学研究

都昌兵，刘文娟

(长沙航空职业技术学院，湖南 长沙 410124)

机动飞行器内碰摩转子的非线性动力学研究

都昌兵，刘文娟

(长沙航空职业技术学院，湖南 长沙 410124)

建立了飞行器内支承在挤压油膜阻尼器上Jeffcott转子的碰摩数学模型，对其在匀速飞行和稳定盘旋两种情况下进行了数值分析。结果表明，机动飞行对转子系统的周期运动、拟周期运动、混沌运动的参数范围甚至稳定性有显著的影响，机动飞行使工作转速低时系统的稳定性降低。

机动盘旋；振动；碰摩；分叉

转静件间的接触（碰摩）是导致旋转机械故障的重要原因之一，在飞行器的转子系统中也经常出现碰摩现象，并导致了严重的故障。碰摩的主要原因有温度或者机械故障导致的质量不平衡，涡轮或者压气机叶片故障、轴承、密封部件故障或者是因为转子不对中等[1]。由于非线性因素和常常出现的混沌运动，碰摩分析是非常复杂的。数值仿真是比较常用的方法，尤其是近年来计算机技术的飞速发展，使得对更加复杂的非线性数学模型进行分析成为可能。

最近20多年来，为了更好地了解碰摩现象，研究者对建立和改善系统的数学模型进行了大量的工作。Muszynaska首先对该问题进行了回顾和总结[1]，包括温度效应、摩擦、撞击、耦合、硬化、振动响应等。Choy和Padovan采用4个假设建立了碰摩的分析模型，并将碰摩过程可以分为4个阶段[2]。Ehrich研究了碰摩系统的混沌和超谐波响应，采用实际的发动机数据进行分析，发现分析结果和实际高度一致[3]。Goldman和Muszynska分析了系统的非线性特征，发现混沌运动的发生主要依赖于模拟冲击运动的模型[4]。Goldman和Muszynska的数值仿真结果表明，系统出现了谐波和次谐波的响应甚至是混沌运动[5，6]，这些现象都得到了试验验证[7，8]。

以上文献在研究转子的碰摩特性时,都将转子设为水平(考虑重力影响),但在实际中当飞行器作机动飞行时,置于飞行器内部的转子轴的位置、转子的运动及受力都将发生变化。重力将在各个方向产生分量；更进一步，当飞行器机动飞行时，将会产生附加的离心力和陀螺力矩，转子的横向不平衡响应就会因此而发生变化。研究飞行器在不同飞行规律下转子的不平衡响应,尤其是故障转子在机动飞行中的响应，将有助于进一步了解动态转子的动力学特性,较真实地反映故障转子的响应特征，为飞行器转子系统的状态监控提供更加可靠的方法。

本文考虑了机动飞行附加离心力和陀螺力矩对系统响应的影响，建立了Jeffcott转子碰摩模型，并对匀速飞行和稳定盘旋两种情况下系统进行了数值仿真，给出了不同于上面文献的研究成果。

1 坐标系和碰摩系统模型

取地面坐标系x'oy'为惯性坐标系，机体坐标系为动坐标系，翼展向左为y向，飞行器对称面向下为x方向，航向为z向。限于篇幅，本文选取稳定盘旋为飞行器的机动动作。在机动盘旋过程中，飞行器有滚转角γ，如图1所示。

图1 地面和机体坐标系

图2 碰摩Jeffcott简图

安装在飞行器内转子系统如图2。其中，m1，m3为轴承质量，m2为转盘质量，e为偏心距，c为油膜厚度，ks为轴的弯曲刚度，kq为圆盘的偏摆刚度，kb为轴承处的弹性支承刚度，cd为圆盘处的阻尼系数，α和β分别为圆盘在绕y和x轴的偏角。Fx1，Fy1和Fx3，Fy3分别为左右支承处的油膜反力。ω为转子工作转速。ωx为稳定盘旋角速度。

假定静子的径向刚度kc，转子和静子间满足库仑摩擦定律，摩擦系数为f，初始时转子和静子间的间隙为δ0（图2）。则碰摩力的无量纲方程为:

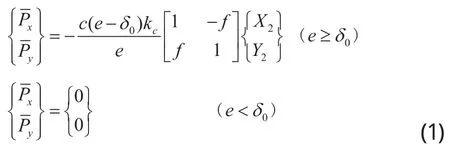
当飞行器机动飞行时，将会产生附加的惯性离心力：

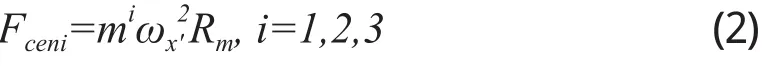
其中Rm为机动飞行半径，离心力作用在x'oy'面内。

根据陀螺理论，附加的陀螺力矩为[9]：

在机体坐标系中，附加的力和力矩为：

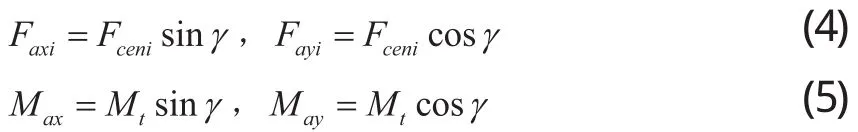
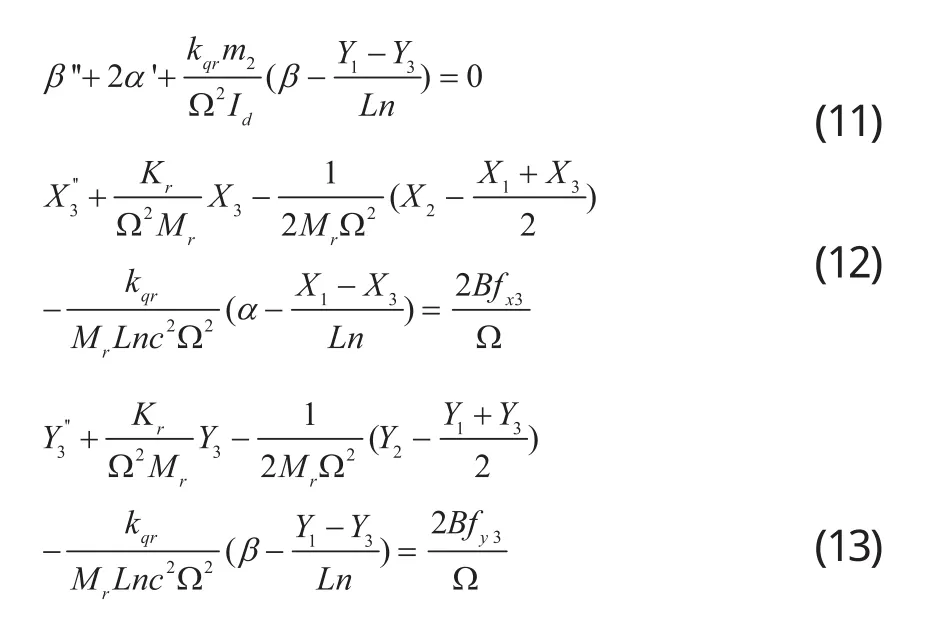
2 数值仿真

为了分析机动盘旋对系统的影响，本文对匀速飞行和稳定盘旋两种情况下的数学模型进行了数值仿真，并且得到了系统的稳态响应。首先不考虑附加的离心力和陀螺力矩，得到系统匀速飞行时的响应，然后对将附加的力和力矩加到相应的方程，求解得到稳定盘旋的响应。系统的参数如表1所示。

采用Runge-Kutta法对数学模型进行求解。求解的频率范围为650-1600rad/s，以4rad/s为增量。为了消除过渡过程，取500个周期后的结果为稳态响应，然后取200个周期的数值进行后处理。

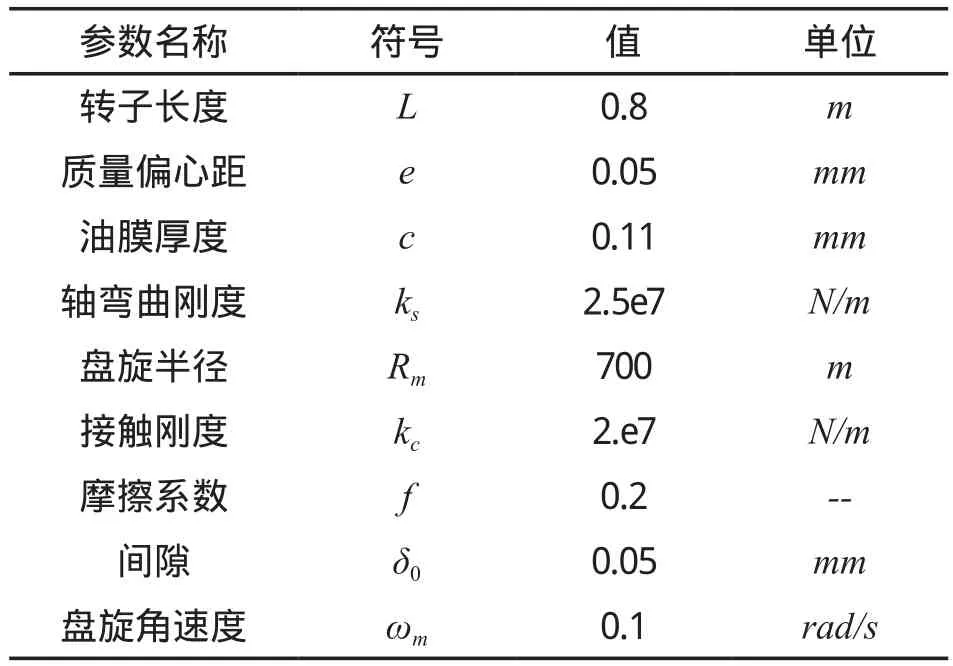
表1 系统数学模型中的物理参数

3 数值分析结果及分析

分叉图是非线性研究中一种非常有效的手段，通过它可以观察到系统所呈现的非线性和混沌特征[11]，在分叉图上，单独的点和多个孤立点代表了周期运动，若干点则表明系统进入了拟周期甚至是混沌运动。因此分叉图被广泛用来分析系统的非线性特征。图3和图4给出了匀速飞行和机动盘旋过程中的系统响应随转速的分叉图。另外，为了详细说明系统的各种工作状态，强调两种模型的不同之处，在转速为840，960，1040时，做出了响应的Poincare切面图和轴心轨迹。

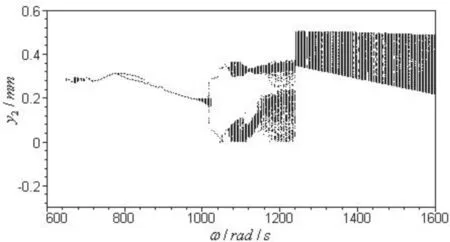
图3 匀速飞行时的分叉分析

图4 机动盘旋时的分叉分析

大体上看，匀速飞行和稳定盘旋时的分叉图形式差不多，都存在周期1、周期2、拟周期和混沌运动，在转速较高时系统以混沌运动为主，但同时也存在周期窗口。转速高时，系统表现出丰富的非线性现象，这是由于碰摩力大大增强，多种非线性因素共同作用的缘故。但是两者也存在很明显的差别。机动盘旋中工作转速较低时（ω=650-1020rad/s）的稳定性不如匀速飞行，此时匀速飞行以周期1运动为主，这主要是因为匀速飞行在工作转速较低时，此时碰摩力很小,系统的不平衡振动占主导地位。而机动飞行由于附加离心力和附加陀螺力矩的影响，碰摩力较匀速飞行大，系统表现出了较强的非线性，出现了拟周期和混沌运动。另外两者都存在一个周期2的运动区间(匀速时出现在ω=800-850rad/s左右，机动盘旋出现在ω=950-1020rad/s左右)，并且随后系统运动是周期1运动，也就是都存在倒分叉现象。但是匀速飞行时该区间的工作转速比机动盘旋时要低。匀速飞行时在1020rad/s-1060rad/s范围内，还存在一个周期2的区域，但是机动盘旋中，该区域已经不明显，说明系统的碰摩已经较为严重，不再是周期运动。在转速为1200rad/s附近，匀速飞行时系统已经进入了混沌运动，而机动中则不存在这一区域，这主要是因为机动附加力的作用使系统更加容易进入严重碰摩，从而产生较强的非线性运动。

图5-7是当工作转速分别为840，960，1080时，平飞和稳定盘旋时系统响应的轴心轨迹和Poincare截面图。匀速飞行和稳定盘旋之间的差别通过这些图可以得到更加明显的表现。当ω=840rad/s时，匀速飞行时，系统响应为周期2的，而机动盘旋过程则为混沌运动。当ω=960rad/s时，匀速飞行时系统为周期1运动，而机动盘旋的响应则为周期2的运动。当ω=1080rad/s时，匀速飞行时系统进入混沌运动，而机动盘旋的响应则为周期1的运动。

图5 ω=840rad/s两种情况的轨迹和Poincare图

图6 ω=960rad/s两种情况的轨迹和Poincare图

图7 ω=1080rad/s两种情况轨迹和Poincare图

对比匀速飞行和稳定盘旋过程中，不同工作转速时系统响应的轨迹和Poincare图，可知机动对系统的响应形式有很大的影响，机动飞行改变了系统周期运动、拟周期运动和混沌运动的参数范围。因此在对飞行器内转子系统的分析中，需要对机动动作进行考虑，只有这样才能了解系统的振动特征；在对振动的监控和诊断时，也必须考虑到机动的影响。

4 结论

本文建立了飞行器内碰摩Jeffcott模型的数学模型，通过对匀速和稳定盘旋情况下的数值仿真，得到同一个物理模型的两组计算结果。结果显示，盘旋过程对模型的振动有明显的影响，机动飞行产生的附加离心力和陀螺力矩和挤压油膜阻尼器的油膜力、碰摩力一起，改变了系统的稳态响应。因此在对飞行器内转子系统进行在线监测和故障诊断时，须考虑机动动作对系统的影响。

[1]Muszynska. Rotor to stationary element rub-related vibration phenomena in rotating machinery-literature survey[J].Shock and vibration Digest,1989，(21)，3-11.

[2]F. K. Choy & J. Padovan. Nonlinear transient analysis of rotor-casing rub events[J].Journal of Sound and vibration.1987，(113)，529-545.

[3]F. Ehrich. Observations of subcritical superharmonic and chaotic response in rotor dynamics[J].Journal of vibration Acoustics Transactions of the ASME, 1992,(114)93-100.

[4]P. Goldman & A. Muszynska. Chaotic behaviour of rotorstator systems with rubs[J].Journal of Engineering for Gas Turbines and Power-transaction of the ASME,1994，(116),692-701.

[5]F. K. Choy, J. Padovan & W. H. LI. Rub in high-performance turbomachinery, modeling, solution methodology and signature analysis[J].Mechanical Systems and Signal Processing, 1988，(2)，113-133.

[6]陈国.航空发动机整机振动耦合动力学模型及其验证[J].航空动力学报,2012,27(2):241-254.

[7]张力,洪杰,马艳红. 航空发动机转子系统建模方法和振动特性分析[J]. 北京航空航天大学学报，2013，39(2): 147-153．

[8]Hou L,Chen Y,Cao Q.Nonlinear vibration phenomenonof an aircraft rub-impact rotor system due to hovering flight[J].Communications in Nonlinear Science and Nu-merical Simulation,2014,19(1):286-297.

[9]王国丽,刘树辉,朱清乐.基于三维有限元模型的双转子-支承系统动力学特性研究[J].北京理工大学学报，2011,31(11): 1292 -1296．

[10]袁惠群，王正浩，闻邦椿．弹性机匣双盘碰摩转子系统的稳定性[J]．振动与冲击，2010，29(8):52-54．

[11]徐敏，廖明夫．机动飞行条件下带挤压油膜阻尼器的Jeffcott转子的振动特性[J]．航空动力学报，2003,18(3):394-401．

［编校：杨 琴］

A Study of Nonlinear Dynamics of Rub Rotor in a Maneuvering Aircraft

DU Chang-bing, Liu Wen-juan
(Changsha Aeronautical Vocational and Technical College, Changsha Hunan410124)

A rub impact mathematical model of a Jeffcott model supported by squeeze film dampers in an aircraft is set up, and a numerical analysis is given in the case of uniform motion and circle flight. The result shows that the maneuver can markedly affect the rotor system’s parameter range for periodic motion, quasiperiodic motion and chaotic motion as well as the system stability. When the rotating speed is low, the maneuver decreases the stability of the system.

maneuver; vibration; rub; bifurcation diagrams

V214.33

A

1671-9654(2017)03-0072-04

10.13829/j.cnki.issn.1671-9654.2017.03.021

2017-06-27

都昌兵（1979- ），男，安徽安庆人，讲师，研究方向为航空发动机维修理论与技术。

本文为2014年湖南省高等学校科学研究项目“现场动平衡技术在航空发动机修理中应用”（编号：14C0008）阶段性研究成果。