积冰条件下飞机飞行包线保护方法研究

张义浦，李 静， 张志春

(1.空军航空大学 军事仿真技术研究所， 长春 130022； 2.空军航空大学 飞行器动力系，长春 130022)

【基础理论与应用研究】

积冰条件下飞机飞行包线保护方法研究

张义浦1，李 静2， 张志春1

(1.空军航空大学 军事仿真技术研究所， 长春 130022； 2.空军航空大学 飞行器动力系，长春 130022)

针对机翼结冰，采用积冰严重程度参数描述积冰对飞机气动特性的影响; 将积冰严重程度参数引入飞机六自由度非线性动力学模型，应用SIMULINK建立了随积冰严重程度而变化的时变飞机仿真模型；以飞机迎角作为关键参数，通过实时在线计算飞机结冰后的失速迎角，建立了开环状态下的飞机结冰包线保护系统；对俯仰姿态下的飞机积冰过程进行了仿真。结果表明：该系统能使飞机保持在安全迎角内，保证积冰条件下飞行安全。

飞机积冰 ；程度参数；包线保护；俯仰姿态保持；仿真

飞机在飞行过程中，如遭遇积冰气象条件，在飞机的所有迎风面都有可能积冰。积冰引起飞机的升力减小、阻力变大、操纵性和稳定性恶化。来自国际民航组织的统计结果表明：1986年及随后的十年间，共有42起飞行事故与飞机积冰有关。国内也有关于积冰引起的飞行事故的报告。2004年，因机翼发生严重积冰现象，一架东方航空公司的客机失事；2006年，因多次穿越结冰区而发生严重积冰现象，空军的一架运八运输机失控坠毁[1]。

区别于传统方法，即极力避免或减轻积冰的产生，美国的Bragg[2]教授提出了“可操作的容冰模式”这一概念，为积冰研究指出了新方向。

防/除冰技术是传统的研究方法，可以阻止或减轻积冰的产生，使飞机在积冰气象条件下能够近似保持正常飞行。基于容冰飞行概念的思想是将特定气象条件下积冰危害程度进行量化分析，得到积冰对飞机稳定性和操纵性的影响程度，作为飞行包线调整和控制率重构的基础，使飞机在积冰气象条件下保持安全飞行[3]。

Bragg等[4]在文献中较为详细的介绍了智能结冰系统对飞行安全的重要作用。Merret等[5]研究了在大气扰动下飞机结冰时如何实现飞行包线保护。国内开展飞机结冰研究起步较晚但发展较为迅速。积冰预测方面的理论研究与实验技术都趋于成熟，建成了技术先进的冰风洞。容冰控制技术的研究目前处于起步阶段，南京航空航天大学[3]与空军工程大学[9]的学者目前走在前列。

本文针对积冰对飞行包线的影响，应用SIMULINK建立了DHC-6飞机六自由度非线性飞机动力学模型，引入积冰严重程度参数η[6]，建立了随积冰严重程度而变化的时变飞机仿真模型；在此基础上，以飞机迎角为关键参数，通过实时计算特定积冰状态下的飞机失速迎角[3]，建立了开环状态下的包线保护系统。仿真结果表明：该方法可使飞机迎角保持在失速迎角范围内，保证了积冰条件下的飞行安全。

1 原理与计算方法

1.1 结冰后飞机气动导数的计算模型

为了克服传统实验研究方法的高成本、周期长等缺点，Bragg[2]提出了一种结构简单、物理意义清晰的根据积冰严重参数预测积冰后飞机气动导数的关系模型。实验证明该模型能取得良好的准确性，模型表示为

(1)

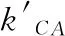
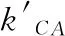
(2)

式(2)中η的定义同ηice类似，但将飞机的机翼弦长和飞行状态考虑在内；kCA为积冰对飞机气动导数及操纵导数影响权重，体现对积冰敏感性，因为η已经将不同飞机的特殊性及飞行状态考虑在内。kCA只与CA类型相关，为固定值，一般通过实验测得。将式(2)代入式(1)，整理后即为具有应用意义的积冰气动导数计算模型[2]：

CA,ice=(1+ηkCA)CA

(3)

1.2 飞机飞行动力学建模

通过数值模拟飞机积冰后的飞行性能和操纵特性，首先需要建立准确的积冰后飞机飞行动力学模型。本文利用SIMULINK仿真软件的FDC工具箱，以DHC-6飞机为例，建立了该机的六自由度非线性飞行动力学模型。该模型包括动力学微分方程和控制方程在内的12个方程，能够准确模拟该机型的飞行性能和操纵规律。

未积冰状态下，飞机的运动方程是状态向量与控制向量的函数，即：

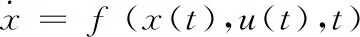
(4)

其中状态向量包括飞机各时刻的速度、角速度、欧拉角以及空间坐标位置：

(5)

控制向量包括飞机各舵面的偏角及发动机的打开系数。通过控制飞机副翼、升降舵、方向舵和襟翼偏角及发动机油门完成对飞机的飞行控制，控制向量表示为

(6)

飞机控制量与状态量之间的关系如图1所示。

图1 飞机控制量与状态量间的关系

非线性常微分刚体运动方程[8]表示为式(7)至式(16)。

力平衡方程：

(7)

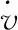
(8)

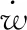
(9)

力矩平衡方程：

(10)

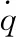
(11)

(12)

运动学方程：

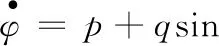
φtanθ+rcosφtanθ

(13)

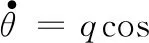
(14)

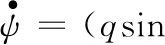
(15)

位置方程：

(16)

其中LVB为机体坐标系向底面坐标系的转换矩阵。

1.3 结冰后的飞机动力学模型

将飞机结冰严重程度参数η引入到干净飞机动力学模型，建立结冰后的动力学模型。η通过影响各个气动力而影响力平衡方程，破坏飞机的力平衡。图2为η对干净飞机气动力影响过程示意图。通过在原有飞机控制方程中引入η，得到结冰后飞机的升力系数、阻力系数以及俯仰力矩系数等，再将这些力和力矩系数代入到力或力矩平衡方程即可求解出飞机结冰后的运动方程。

图2 飞机结冰后气动力计算过程

积冰飞机的运动方程是状态向量、控制向量以及结冰参数的函数[8]。和干净飞机的运动方程相比，结冰飞机的运动方程多了参数η。

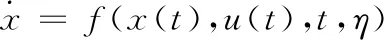
(17)

仿真过程中每一时刻的η都只与此时刻的积冰严重程度相关。时间每推进一步，根据此时刻的η值对飞机的气动模型进行一次更新，得到此时刻飞机的气动力和各状态量值，从而实现模型随η而变化的时变系统的仿真。

1.4 飞机纵向自动驾驶模型

本文在飞机积冰动力学模型的基础之上，借鉴文献[9]中自动驾驶系统的设计原理，建立了积冰情况下飞机俯仰姿态保持模式(PAH)自动驾驶仿真系统。该模式是飞机纵向控制系统的核心，PAH的核心结构如图3所示。

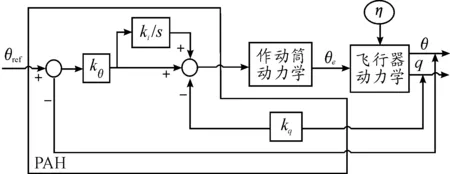
图3 俯仰姿态保持模式框图

PAH的目标是跟踪驾驶员输入的俯仰角参考值θref，采用经典的PID控制原理设计控制器。PAH通过调整升降舵使俯仰角逐步逼近θref。比例和积分控制器用来保证减少俯仰角稳态误差。因反馈而造成的短周期模态阻尼减小现象由微分控制器的俯仰角速率反馈补偿。ki，kθ和kq是控制器的增益系数，符合不结冰飞机随速度的调参规律[10]。

控制律可以表示为

(18)

2 包线保护系统构建

2.1 关键参数选取

关键参数指那些超出限制可能导致飞机失速的飞行状态参数。定义飞行包线的关键参数向量y是状态向量x和控制向量u的函数，即：

y=f(x,u)

(19)

这样，求解关键参数的安全范围也就转化为求解y的极限值ylim。ylim受结冰参数η影响：

y=f(x,u,η)

(20)

ylim=ylim(η)

(21)

这样包线保护系统的设计就简化为通过约束控制向量使关键参数保持在限制范围之内，即：

(22)

2.2 边界条件计算

大量的风洞试验结果表明：飞机发生积冰时，积冰后机翼的最大升力系数CLmax与某定值迎角下积冰前后升力系数变化量ΔCL之间存在一定的关系，图4为关于ΔCL与CLmax的实验结果。

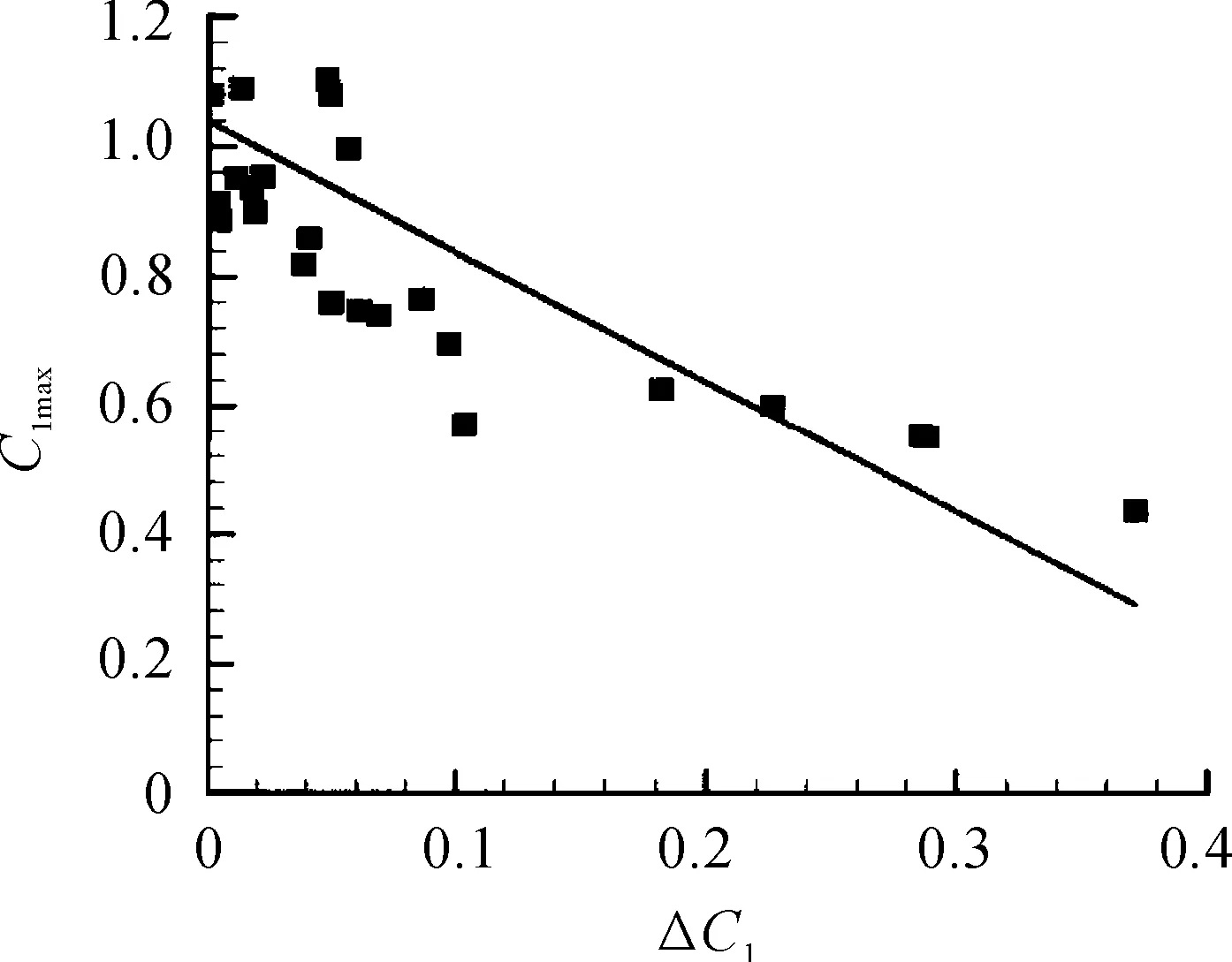
图4 某定α值时最大升力系数与结冰升力 系数的关系曲线

图4中可看出，CLmax与ΔCL近似成线性关系，大量的冰风洞试验结果显示，当飞行迎角在0°～11°内时，这种线性关系都存在。而飞机失速迎角又是CLmax的函数，那么在同一个配平迎角下，失速迎角是结冰前后ΔCL的函数，通过在线计算，得到任意时刻的失速迎角αstall。

以迎角为4°为例，ΔCL是积冰后机翼相对于干净机翼的升力系数增量，CLmax为某积冰严重程度参数下的最大升力系数[2]，则

ΔCL(α=4°)=|ΔCL,iced(α=4°)-ΔCL,clean(α=4°)|=g(α=4°)(η)

(23)

CLmax=CLmax,clean-k1ΔCL=CLmax,clean-

k1(CL,clean(α=cout)-CL,iced(α=cout))

(24)

导出失速迎角与CLmax的线性关系[2]：

αstall=(CLmax+CL0)/CLα

(25)

式(25)中CL0为迎角为0°时升力系数，CLα为升力线斜率。

可得到结冰条件下αstall的计算模型

αstall=f(ΔCL)=f[g(η)]

(26)

这个模型就可以用来估计小迎角飞行时的迎角极限值。实际飞行时，根据结冰严重程度，确定结冰参数η，计算得到ΔCL，获得失速迎角[2]αstall。

2.3 操纵指令确定

随结冰加重，飞行包线将缩小，极限迎角将减小。若继续按不结冰飞机的迎角飞行，飞机很可能超出原定飞行包线，发生飞行事故。因此，在线计算得到实时的飞行包线后，必须修改控制律。对于纵向保持模式来说，即通过调整升降舵偏角，使飞机迎角保持在安全飞行包线内。

在仿真过程中，设定当前时间步t1的俯仰角为θ1，驾驶员输入指令为θin,1；前一时间步t0时刻的俯仰角为θ0，驾驶员输入为θin,0；t1时刻的俯仰角改变极限值为θref,1。“指令限制器模块”自飞机开始积冰时启动，边界保护系统每Δt时间计算一次，本文取Δt为1 s。每经过Δt，通过当前时刻的飞行状态得到俯仰角改变极限θref；通过将t1时刻θ1和θref,1的和与t0时刻的驾驶员输入指令θin,0进行对比，若在安全边界内，则保持t0时刻的输入指令θin,0；若超出安全指令范围，则改变输入指令θin,1为θ1+θref,1。预估判断的操纵准则如图5所示。

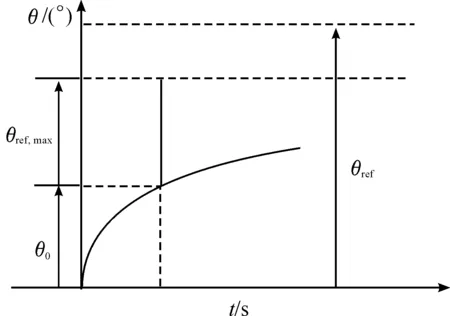
图5 预估判断的操纵准则

用等式来描述飞机的闭环PAH模型：

x=g(x,u=θin,η)

(27)

在飞行中，可以假定θin保持当前值，预估迎角极限是否被超越。如果超越，降低θin值保持飞机在包线内。

2 模型准确性验证

为验证本文采用的六自由度非线性模型的准确性，选择DHC-6飞机作为算例模型，仿真采用与飞行实验相同的条件以及操纵动作。实验条件如下(表1)。

表1 初始飞行参数

仿真过程中飞行高度、速度、迎角的变化历程[8]与飞行试验数据的对比如图6所示。

通过结果比对发现，仿真取得良好的结果。与真实气象条件下的飞行实验变化趋势相同，数值误差能够控制在可接受的范围内。误差存在的主要原因是理想情况下的仿真实验没有将反映周围环境干扰的小扰动因素考虑在内。

基于以上对比和对误差的分析，本文认为所采用的六自由度非线性模型可以作为分析DHC-6飞机操纵性的仿真模型。

3 仿真结果及分析

为了验证本文所提方法的正确性，使用文献[10]中的数据，初始飞行高度2 300 m，飞行速度54 m/s，飞机结冰严重程度参数η在0～50 s时间内从0线性变化到0.2。为了确保飞机不因计算误差而超出安全边界，取计算结果的6%为安全裕度。俯仰姿态保持模式参考指令θin=4°，控制器增益系数ki=0.5，kθ=-2.0，kq=0.3。积冰开始25 s后飞行员发现积冰发生，打开包线保护系统。仿真结果图清楚地显示了飞机在包线保护下和没有保护下的飞行状态。

图7(a)是飞机迎角在两种情况下的响应曲线。可以清楚地发现没有包线保护的情况下飞机迎角超过安全边界进入失速区，飞行安全不能得到保障。启动包线保护系统后，可以有效地避免这种情况。同时系统还可以避免人为操纵失误导致的飞行事故，可以根据实际飞行安全的需要自动调整输入指令值，如图7(b)所示，俯仰角没有稳定在参考指令值。

综上分析可知，本文提出的边界保护系统行之有效，能够通过控制升降舵偏角保证机翼迎角在安全范围内，避免飞机进入失速区飞行。需要指出的是，本文介绍的情况是基于自驾仪(PAH)模型的，能够根据飞行情况进行实时调节；对于飞行员模型，则需要考虑人为的判断延时和传动系统动作的延时，设置提前告警。

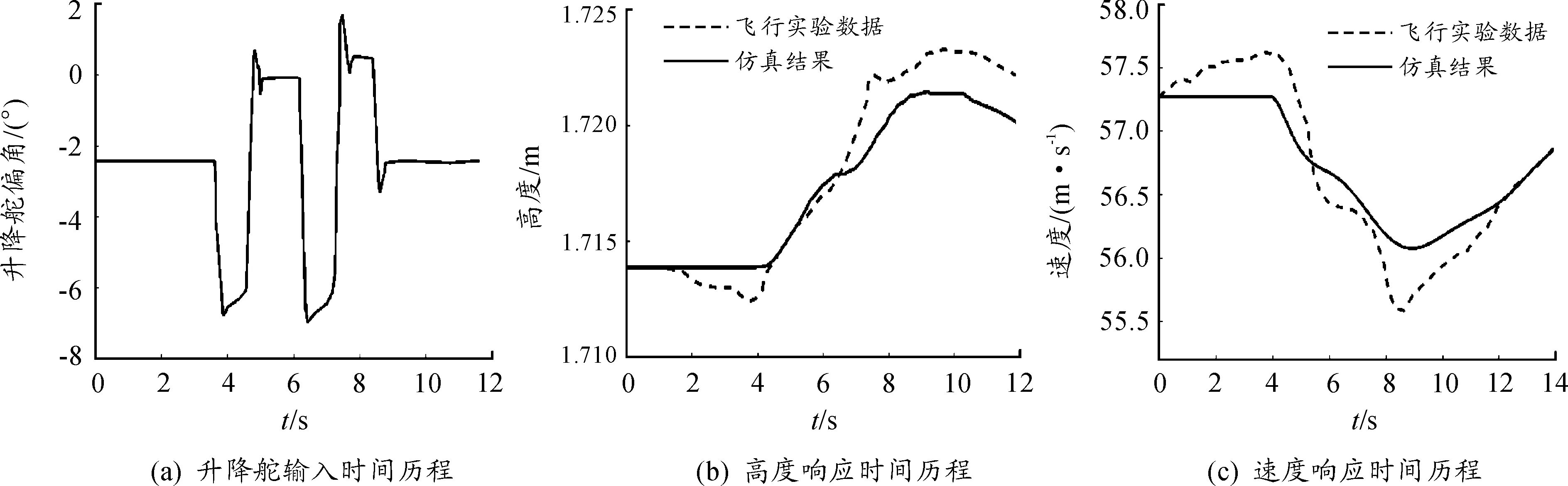
图6 仿真结果与飞行试验数据

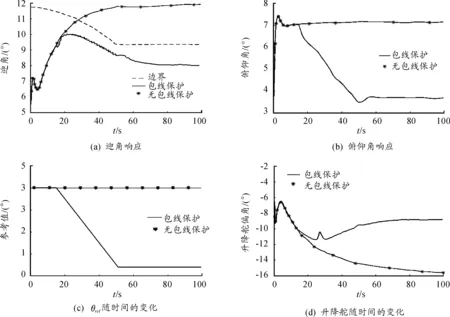
图7 包线保护情况下积冰飞行仿真结果

4 结论

本文利用积冰程度参数η，建立了随积冰严重程度而变化的时变飞机仿真模型；分析了积冰后飞机的失速特性；设计了飞机自动驾驶闭环仿真系统；设计了积冰气象条件下的飞行包线保护系统，为容冰控制规律的研究打下基础；通过仿真，验证了本文所述方法的有效性，同时得出几点结论：

1) 将η引入飞机模型所构成的时变仿真模型能够反映飞机积冰过程，可以作为研究积冰对飞机操纵性影响的仿真模型。

2) 飞机在低速飞行状态时，需要更大的配平迎角，如果此时发生积冰情况，飞机失速的风险更大，因此飞机在起降过程中如果遭遇结冰尤为危险。

3) 积冰对自动驾驶飞机指令跟随有一定影响，导致飞行迎角和操纵舵面偏角增大，不仅增大了失速发生的概率，而且可能导致操纵舵面的饱和，对飞机操纵性能造成不利影响。

4) 建立了可信的飞行力学模型，对积冰后飞机飞行的仿真可以代替飞行实验[11]。

[1] 易贤.飞机积冰的数值计算与积冰实验相似准则研究[D].北京：中国空气动力研究与发展中心研究生部,2007.

[2] BRAGG M B,HUTCHISON T,OLTMAN R，et al.Effect of Ice Accretion on Aircraft Flight Dynamics[R].AIAA-2000-0360,2000.

[3] 张智勇.结冰飞行动力学特性与包线保护控制律研究[D].南京：南京航空航天大学,2006.

[4] BRAGG M B,BASAR T,PERKINS W R,SELING M S,VOULGARIS P G.Smart Icing Systems for Aircraft Icing Safety[R].AIAA 2002-0813,2002.

[5] MERRITT J,HOSSAIN K N,BRAGG M B.Envelope Protection and Atmospheric Disturbances in Icing Encounters[R].AIAA 2002-0814,2002.

[6] BRAGG M B.HUTCHISON T,MERRITT J.Effect of Ice Accretion on Aircraft Flight Dynamics[R].AIAA 2000-0360,2000.

[7] ROBER W D,GLEN A D.Icing encounter flight simulator[J].Journal of Aircraft,2006,43(5):1528-1537.

[8] 徐忠达,苏媛,曹义华.积冰对飞机操纵性的影响与仿真[J].北京航空航天大学学报,2012,38 (7):941-946.

[9] 王小龙,徐浩军,薛源,朱和锉,裴彬彬.俯仰姿态保持模式下飞机结冰边界保护方法[J].航空动力学报,2016,36(9):2087-2090.

[10] 应思斌,艾剑良.飞机结冰包线保护对开环飞行性能影响与仿真[J].系统仿真学报,2010,22(10):2273-2275.

[11] 刘烨,王新民,周健.无人机纵向控制律设计以及纵向轨迹跟踪仿真研究[J].科学技术与工程,2011，31(16):9008-9011.

(责任编辑杨继森)

IcingEffectsonAircraftHandlingCharacteristics

ZHANG Yipu1， LI Jing2， ZHANG Zhichun1

(1.Military Simulation Technology Research Institute, Aviation University of Air Force, Changchun 130022, China; 2.Department of Aircraft Aerodynamic, Aviation University of Air Force, Changchun 130022, China)

Aiming at the icing problem of wing, a icing degree parameter was used to describe the ice effects on aircraft aerodynamic parameter; This parameters was introduced into nonlinear six degrees-of-freedom dynamic model of plane; A time-varying simulation model was established with SIMULINK, which varying with this parameter; Based on the attack angle of the aircraft, a aircraft icing envelope protection system is established by the real-time calculation of the stall attack angle. A pitch attitude keeping model was simulated. The results displayed that the system can keep the aircraft in a safe attack angle. Thus the icing conditions of flight safety can be ensured.

aircraft icing; degree parameter; envelope protection; pitch-hold model; simulation

2017-03-22；

：2017-04-20

：吉林省自然基金资助项目(20130101069JC)

张义浦(1992—)，男，硕士研究生，主要从事飞行器仿真研究。

10.11809/scbgxb2017.09.038

format:ZHANG Yipu，LI Jing，ZHANG Zhichun.Icing Effects on Aircraft Handling Characteristics[J].Journal of Ordnance Equipment Engineering,2017(9):178-183.

V244.1+5

：A

2096-2304(2017)09-0178-06

本文引用格式：张义浦，李静， 张志春.积冰条件下飞机飞行包线保护方法研究[J].兵器装备工程学报，2017(9):178-183.