基于空间聚类的中压配电网网格优化划分方法

，，

(1.中国能源建设集团广东省电力设计研究院有限公司，广东 广州 510663； 2. 广州供电局有限公司，广东 广州 510620)

基于空间聚类的中压配电网网格优化划分方法

陈超1，李志铿1，苏悦平2

(1.中国能源建设集团广东省电力设计研究院有限公司，广东 广州 510663； 2. 广州供电局有限公司，广东 广州 510620)

网格化规划方法是解决城市配电网由于缺乏面向远景的、持续和一贯的目标网架及其过渡过程而导致线路接线混乱、无序、联络复杂等问题的有效技术手段。网格的科学合理划分是网格化规划中必须首先解决的关键问题。然而，目前网格的划分仍依赖规划人员的主观经验或笼统的技术原则，不仅工作量巨大，而且难以满足技术经济性和方案合理性。为此，在构建网格划分综合评价指标体系的基础上，提出了基于空间聚类算法的网格优化划分数学模型及其求解方法，为进一步推进网格化规划的工程应用奠定了基础。基于实际区域配电网的算例分析验证所提模型和算法的有效性。

配电网；网格化规划；网格划分；空间聚类

0 引 言

长期以来，中国经济社会处于快速发展阶段，城市配电网的规划建设也相应地以满足近期负荷增长为首要目标，由此导致配电网规划缺乏持续和一贯的目标网架及过渡安排，不同规划人员以及不同时期的规划方案，往往大幅改动甚至全面推翻上一阶段的规划成果，造成中压配电网网架结构混乱、线路路径交叉迂回、无序和复杂联络等问题突出，不仅严重影响了配电网故障处理和运行调度，而且降低了设备运维管理和营销服务等业务效率。

为此，国内多个城市相继开展了基于网格的配电网规划[1-4]。网格化配电网规划，是将复杂的配电网划分为多个相对独立的局部区域，每个局部供电区域，即网格，由若干组典型接线直接供电。由于网格之间相对独立，因此，规划人员只需针对网格内部的负荷发展情况和电网现状，规划目标网架及其过渡过程，从而使整体配电网的目标网架得以持续贯彻。此外，电网企业还能够以网格承载配电网规划、建设、运行调度、设备运维和营销管理等多个环节，实现多环节的闭环整体优化。

显然，网格的科学合理划分是网格化配电网规划的关键问题。目前，尽管供电企业一般制定了相应的网格划分原则，如要求网格应以主干道路、河流或山丘等地理屏障为界等，但是在具体的网格化规划实践中，网格划分仍主要依赖规划人员的主观经验。由于网格的划分涉及了负荷划分、用户切割、网架改造等诸多环节，因此，仅凭规划人员的主观经验或笼统的技术原则，实际上难以满足技术经济性和技术合理性方面的要求。而且，面对规模庞大的城市配电网，人工进行网格划分，需要不断重复指标计算和网格边界调整等工作，涉及极大的工作量，不利于网格化规划工作的工程应用。

为此，这里首先从技术合理性和经济性等方面，构建了网格划分综合评价指标体系。在此基础上，以技术合理性和经济性综合最优为目标，考虑地理边界和行政边界约束，建立了中压配电网的网格优化划分数学模型，提出了基于空间聚类算法的模型求解方法，并以某试点区配电网为例，对上述模型和算法的有效性进行了验证。

1 配电网网格化

1.1网格的定义

配电网网格化[5-6]，是指按网架现状、负荷分布、地理分界等实际情况，将复杂的配电网划分为多个相对独立的网格。一般规定每个网格由若干组标准接线直接供电，因此，网格之间不仅是有若干个街区组成，在地理上相对独立，而且在电气上也相对独立，仅在高压变电站层面有电气联系。此外，各个网格的负荷发展特性应相对接近，如负荷饱和、负荷快速发展和负荷不确定等。

1.2一般划分步骤

在目前的网格化规划实践中[7]，通常遵循自下而上、上下结合的划分思路，往往需要反复修正和评价，具体包括：

1) 根据低压台区的负荷以及其他地块的负荷预测，综合考虑现状网架结构、地理分界，按区域总负荷不超过某一限值为原则，将若干个台区组成一个中压网格，初步形成中压网格的划分方案。

2) 根据一定的评价指标体系，对初步划分方案进行分析。

3) 根据评价结果的优劣，反复修正网格划分方案，直至指标满足要求。

可见，对于规模庞大的城市配电网，上述划分步骤不仅难以保证划分方案的技术合理性，而且，由于需要反复修正网格划分方案，因此需要极大的工作量，严重限制了网格化规划的适用性。

2 网格优化划分模型

2.1目标函数

网格划分的本质，是将现状配电网中的配电变压器，划分入各个网格。为便于配电网运维，网格的边界显然应尽量以高速公路、主干道路、河流和山地等地理屏障为界。因此，应尽量将距离较近的配电变压器划归入同一网格，而将受地理阻隔的配电变压器划入不同的网格。而且，将地理上分布较近的配电变压器划归入同一网格更有利于网格划分后的网架调整。

综上所述，定义配电变压器Ti与聚类中心Cj的距离dij(Ti,Cj)为

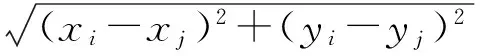
(1)

式中：(xi,yi)和(xj,yj)分别为Ti和Cj的坐标；λij为Ti和Cj的距离系数，表征了两者受到地理阻隔的程度，其取值如表1所示。

表1 距离系数λij的典型取值

显然，当dij满足式(2)时，Ti属于聚类中心Cj：

d(Ti，Cj)=minm=1，2，…Md(Ti，Cm)

(2)

式中，M为聚类中心的数量。

因此，网格优化划分模型的目标函数应为

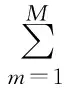
(3)

2.2网格优化划分模型

由于配电变压器归属于各自的线路，因此，将某一线路划归某个网格时，意味着网格外的配电变压器将切割至其他线路；而配电变压器的切割涉及用户停电和网架改造，对网格划分方案可行性和技术经济性至关重要：因此，网格划分应尽量减少配电变压器切割。为此，定义平均用户切割率k为

(4)

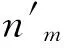
综上所述，根据式(3)所示的目标函数，可构建网格优化划分模型，如式(5)所示：

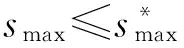
(5)

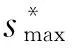
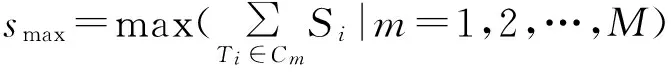
3 遗传K-均值空间聚类算法

显然，如式(5)所示的网格划分是对于配电变压器地理位置在约束条件下的空间划分问题。对此，K-均值方法[8-11]是目前应用广泛的方法之一，具有算法简单、计算速度快等特点。然而，由于K-均值方法的聚类结果依赖于初始值选取，且通常采用梯度法求解极值，因此K-均值方法对初始选值非常敏感且收敛时易陷入局部极值。

由于遗传算法的高效全局优化搜索优点[12-15]，可将遗传算法与K-均值算法相结合，从而克服K-均值算法的上述问题。

3.1染色体编码及初始种群

染色体的长度对遗传算法的收敛速度有重要影响，因此，采用基于聚类中心的编码方式：

S=P1P2…Pj

(6)

式中，Pj为j个聚类中心，j=1,2,…,m。

3.2适应度函数

根据式(5)所示的目标函数，构建遗传个体的适应度函数如式(7)：

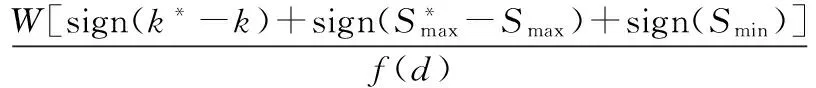
(7)

式中，W是预设的取值较大的正数。

3.3遗传操作方法

1)选择。遗传算法的个体选择机制是使适应度高的个体具有较大的生存机会。然而，为减少超级个体的影响，采用以适应度相对值作为选择标准的锦标赛选择方法。

2)交叉。为了更有效地产生新的有意义的个体，保持群体的多样性，采用基于最近邻基因匹配的交叉运算方法。

3)变异。遗传算法的变异机制是保证算法全局寻优能力的关键，因此变异算子的选择对最终全局最优解的获得有重要影响。这里采用随机变异方法，即变异算子按基因位进行，根据变异概率，发生变异的基因位被随机选取的对象取代。

3.4算法步骤

遗传K-均值空间聚类算法流程如下：

1)确定遗传参数，产生初始种群P(0)；

2)根据式(7)计算种群P(t-1)中各个体的适应度；

3)对P(t-1)作选择操作，得到下一代群体P(t)；

4)对P(t)作交叉操作；

5)对P(t)作变异操作；

6)若到达最大代数或P(t-1)与P(t)中类内离散度和之差ε在给定限差内，继续执行，否则转步骤2)；

7)输出结果。

3.5空聚类的影响

在对某一个体进行网格划分时，可能出现空聚类。此时，可采用如下的方法进行调整：对某个空聚类Gi，将属于非空聚类Gj但离Gj最远且离Gi最近一个对象划归Gi；重复上述过程，直至划分中不再有空的聚类为止。

4 算例分析

4.1区域概况

选取的试点片区以广深高速公路为界分为南北两大区域：北部试点区域范围是东起开创大道(广深高速-开源大道段)，西至大观路，南至广深高速公路，北至广汕公路与开创大道(开源大道-广汕公路段)，面积约26 km2；南部试点区域范围是东起科丰路，西至科珠路，南起科林路，北至广深高速公路，面积约4.6 km2。试点片区南北两区域面积合计约30.6 km2。

截至2015年年底，试点片区内有高压变电站9座，共有10 kV间隔326个，已用间隔197个(区域内占用间隔138个)；10 kV供电线路142回，其中公用线路92回，专用线路50回；配电变压器1 028台，合计容量1 304.71 MVA，其中，公变92台、容量58.53 MVA，专变936台、容量1 246.19 MVA。

4.2划分结果

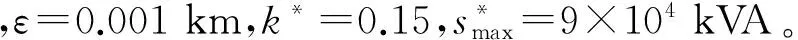
按所提方法，网格划分结果如图1所示。表1给出了所提方法与基于规划人员经验的划分结果的目标函数取值对比结果。

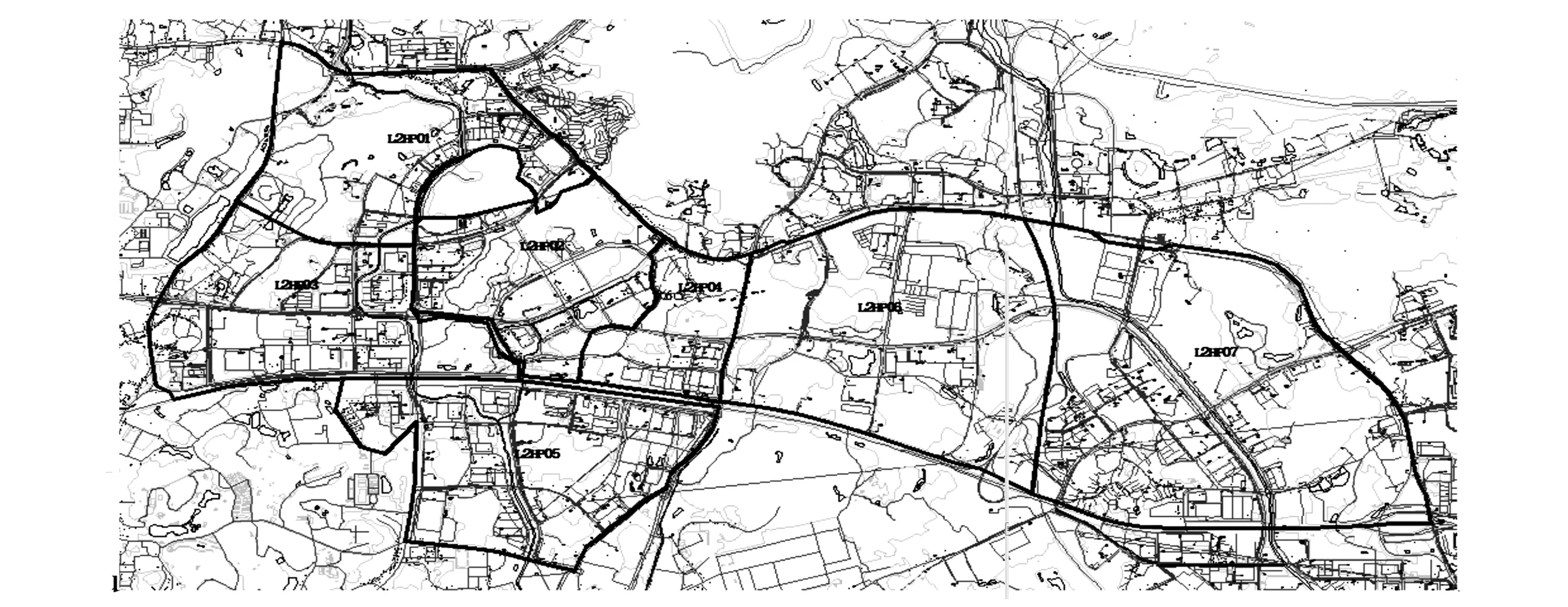
图1 网格划分结果

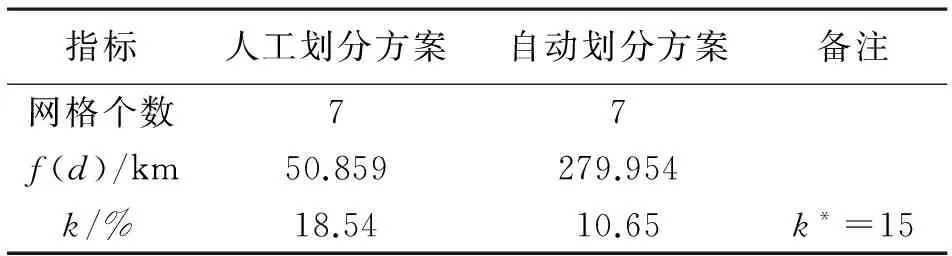
指标人工划分方案自动划分方案备注网格个数77f(d)/km50.859279.954k/%18.5410.65k*=15

对于预设的网格个数，人工划分方案和自动划分方案都按主干道路将本区域进行了网格划分。由表1可知，人工划分方案的f(d)值和k值远大于自动划分方案，表明在该方案下，不仅配电变压器间的相对位置较远，而且涉及大量的网架改造和用户切割。可见，自动划分方案显然优于人工划分方案。

5 结 论

网格的科学合理划分是网格化规划中必须首先解决的关键问题。前面在构建网格划分综合评价指标体系的基础上，提出了基于空间聚类算法的网格优化划分数学模型及其求解方法。基于某试点片区配电网的实际算例表明，该模型和方法准确、有效，解决了传统人工划分方法工作量巨大且难以满足技术经济性和方案合理性的问题，为进一步推进网格化规划的工程应用奠定了基础。

[1] 张茂群, 田万军, 王登政, 等. 基于“网格化”的配电网空间布局规划 [J].农村电气化，2016(5):13-15.

[2] 卫泽晨, 赵凤展, 王佳慧, 等. 网格化中低压智能配电网评价指标体系与方法 [J]. 电网技术，2016,40(1):249-255．

[3] 李健， 马彬, 张植华，等. 基于网格的城市配电网优化规划方法研究[J]．南方能源建设，2015,2(3)：38-42．

[4] 张峰，张建华．基于网格化管理的城市中心区智能配电网规划研究[J]．科技风，2013(16)：230．

[5] 姚刚, 仲立军, 张代红, 等．复杂城市配电网网格化供电组网方式优化研究及实践[J]．电网技术，2016,38(5): 1297-1301．

[6] 王大雷. 网格分析法在城乡配电网规划中的应用与研究[D]．北京：华北电力大学, 2012．

[7] 李海涛, 孙波, 王轩．配电网网格化规划方法及其应用[J]．电力系统及其自动化学报，2015,27(增刊): 33-37．

[8] 傅德胜, 周辰．基于密度的改进K均值算法及实现[J]．计算机应用, 2011,31(2): 432-434．

[9] Joshi K D, Nalwade P S. Modified K-means for Better Initial Centers[J]．International Journal of Computer Science and Mobile Computing, 2011,2(7): 219-223．

[10] G W Ma , ZH Xu , W Zhang, et al. An Enriched K-means Clustering Method for Grouping Fractures with Meliorated Initial Centers[J]．Arabian Journal of Geosciences, 2015，8(4):1881-1893．

[11] 吉兴全, 韩国正, 李可军，等. 基于密度的改进K均值聚类算法在配网区块划分中的应用[J]．山东大学学报(工学版), 2016,46(4):1-6．

[12] 边霞, 米良. 遗传算法理论及其应用研究进展[J]．计算机应用研究, 2010,27(7): 2425-2429．

[13] Wang Lei, Tang Dunbing. An Improved Adaptive Genetic Algorithm Based on Hormone Modulation Mechanism for Job-Shop Scheduling Problem[J]. Expert Systems with Applications, 2011, 38(6): 7243-7250.

[14] 马永杰, 云文霞. 遗传算法研究进展[J]．计算机应用研究, 2012,29(4): 1201-1206．

[15] 曹昉, 孟琦斌, 苗培青，等. 基于改进加权Voronoi 图和遗传算法的变电站规划[J].电网技术, 2015,39(2): 511-516．

The gridding planning method is an effective technical method for solving the problems that the lines are confused, disordered and connected complexly because the urban distribution network planning lacks of perspective, continuous and consistent target grid and its transition process. The reasonable grid division is the key problem that must be solved firstly in gridding planning. However, the current grid division still depends on subjective experiences of the planning staff or general technical principles, which leads to huge workload and makes the planning not meet the economic efficiency and rationality. So the grid division evaluation index system is constructed. On this basis, the mathematical model of optimal grid division and its solutions based on spatial clustering is proposed for advancing engineering application of gridding planning. The validity of the proposed model and its solutions are verified with a case of actual distribution network.

distribution network; gridding planning; grid division; spatial clustering

TM715

：A

：1003-6954(2017)04-0020-04

2017-03-01)

陈 超(1985)，工程师，研究方向为自动化系统设计、配电网规划等； 李志铿(1981)，高级工程师，研究方向为配电网规划、设计等。