高压直流换流变压器油纸绝缘线性与非线性电场分析
刘文里,白仕光,李祎春,李佳欣
(1.哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨150080;2.大唐东北电力试验研究所有限公司,吉林 长春 130015;3.内蒙古东部电力有限公司物资分公司,内蒙古 呼和浩特 010000;4.国网通辽供电公司,内蒙古 通辽 028000)
高压直流换流变压器油纸绝缘线性与非线性电场分析
刘文里1,白仕光2,李祎春3,李佳欣4
(1.哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨150080;2.大唐东北电力试验研究所有限公司,吉林 长春 130015;3.内蒙古东部电力有限公司物资分公司,内蒙古 呼和浩特 010000;4.国网通辽供电公司,内蒙古 通辽 028000)
换流变压器油纸绝缘材料的电导率受电场强度与温度的影响呈非线性变化。为研究材料非线性对换流变压器极性反转电场分布的影响,对油纸绝缘电导率的非线性变化规律进行了数值拟合,利用RC等效电路进行了计算与分析,并运用ElecNet有限元软件对一台±400 kV换流变压器网侧和阀侧绕组端部电场进行了仿真。计算与仿真结果表明非线性材料极性反转完成时油中最大电场强度为线性材料的78%,但稳态时油中电场强度是线性情况下的36倍。电导率的电场强度非线性会均化由温度梯度带来的电场梯度。最后根据计算与仿真结果提出绝缘的改进方向。
换流变压器;电场分布;极性反转;油纸绝缘;非线性材料
0 引 言
特高压直流输电系统中,换流变压器是最重要的设备之一,其运行可靠性直接影响电网的稳定[1]。运行中的换流变压器长期承受着交流、直流和极性反转电压的作用,故对其绝缘性能的要求异常严格[2-3]。近年来换流变压器运行过程中频频出现故障,部分缘于其绝缘结构设计方面的缺陷[4]。目前,换流变压器采用油纸复合绝缘,薄纸筒小油隙结构[5],受电场强度与温度的影响,两种材料的电导率呈非线性变化,致使换流变压器的电场分布更为复杂。
据统计,关于油纸绝缘非线性方面的研究较少。Takashi E、Rongsheng L等人根据测量结果得出随着电场强度、温度的升高油纸绝缘材料的电导率呈指数规律上升的结论,但由于设备水平的局限性无法给定具体函数[6-7]。LI Jinbiao、张施令等人研究了非线性电场的计算方法,提出可以利用ANSYS有限元软件运用迭代法进行仿真计算;但运算过程非常繁琐、误差较大[8-9]。刘刚拟合了Takashi E的实验数据,并对换流变压器局部电场进行仿真,认为非线性材料电场强度最大值比线性材料小50%;但所用数据过于陈旧,采用2阶C-N差分法精确度不足,所使用的模型也并非实际模型[10]。关健昕研究了材料非线性对阀侧出线绝缘裕度的影响,认为考虑非线性时套管裕度过大[11]。
为改进换流变压器的绝缘结构,提高其稳定性,本文通过油纸绝缘的RC等效模型,建立了数学模型,并利用Matlab 4阶Runge-Kutta算法分析了非线性油纸绝缘的电场分布及电荷量变化情况,根据换流变压器的实际尺寸建立了电场仿真模型,利用ElecNet有限元软件2阶N-R高次迭代算法计算出不同温度分布下非线性油纸绝缘结构中的电场分布。由于换流变压器的故障主要发生在极性反转时[12-14],故本文着重研究了极性反转电压下材料非线性对电场分布的影响。
1 油纸绝缘分析
1.1 线性油纸绝缘的分析
1.1.1 RC模型及极性反转电压
目前,利用如图1所示的平板电极RC等效电路来分析和计算双层介质电压分布的方法已趋于成熟,本文沿用此方法来分析极性反转电压下油纸绝缘结构中的电场分布情况。极性反转电压如图2所示。加压瞬间,电压按电容分布;电场分布达到稳态时,电压按电阻分布;最后为极性反转情况。文献[15-19]证实:极性反转完成瞬间油中出现极高的电场强度,而油的最大耐受场强比纸板低,故本文主要研究油中电压变化。
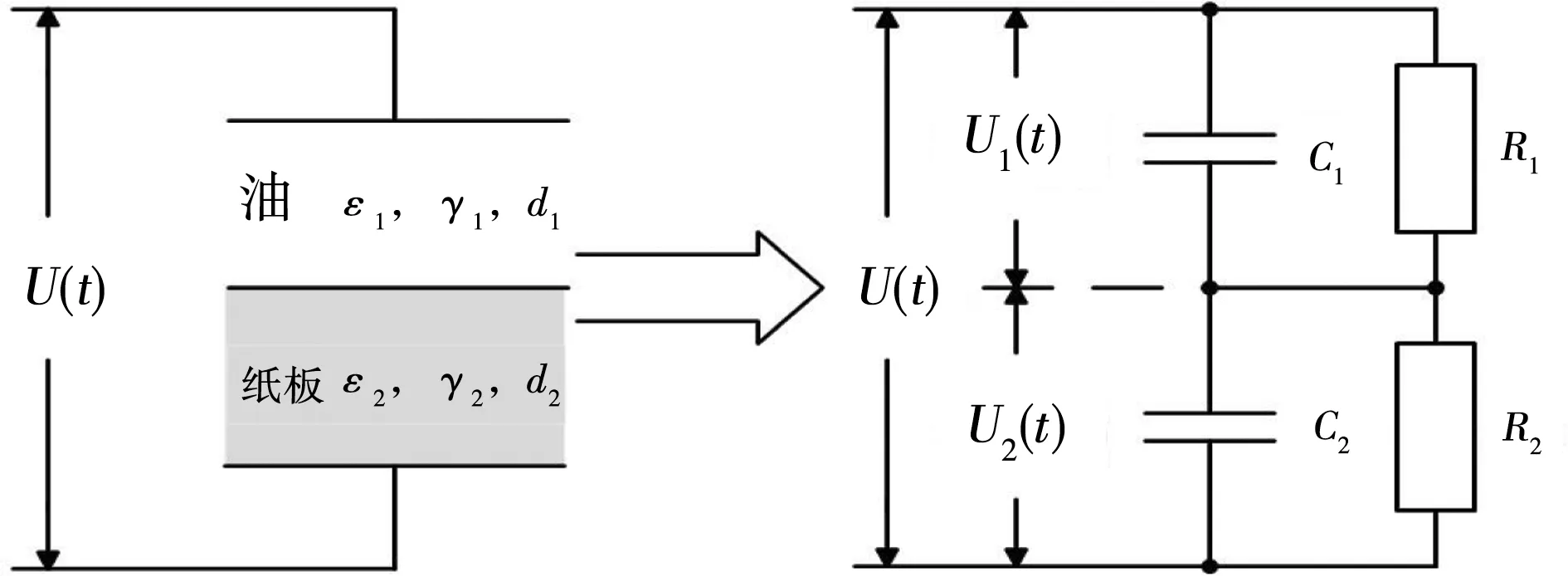
图1 油纸绝缘结构及其等效电路Fig.1 Oil-board insulation structure and its equivalent circuit

图2 极性反转电压Fig.2 Polarity reversal voltage circuit
1.1.2 数学模型
当t=t0(t0→-)时,RC等效模型两端开始施加电压,电压按电容分布,可得:

当t=0时,认为电压分布已达到稳态,电压按电阻分布,可得:

可用三要素法计算出:

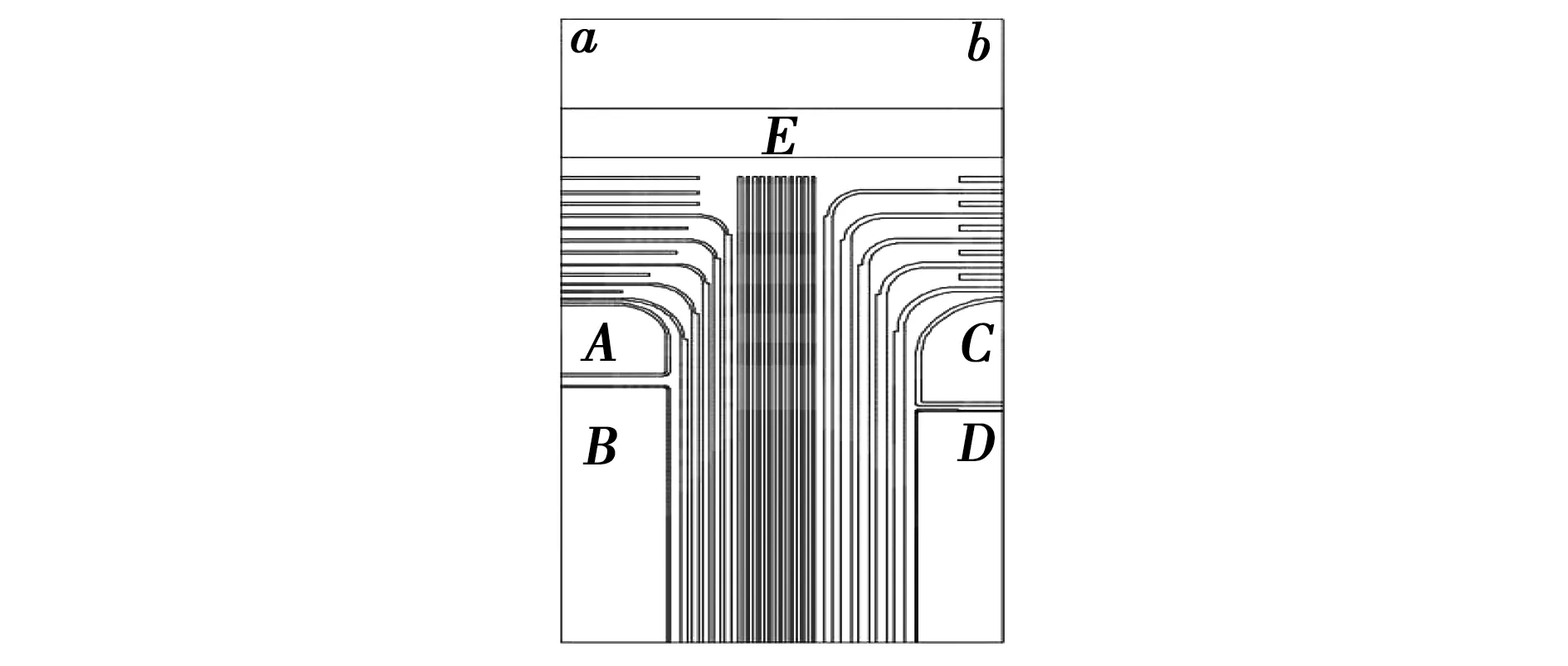
当0 (1) 此方程为线性一阶微分方程,其通解为 (2) 将K1代入式(2)可得 当t>ΔT时,仍可按照三要素法计算,可得 经计算该结果与全电流相等方法所求得的结果完全一致。 通过分析数学模型可知:U1(t)的幅值与γ2d1/(γ2d1γ1d2)呈正比关系,实际工程中γ1>>γ2,故增大γ1或d2均可降低U1(t)的幅值。 U1(t)最大值出现在t=ΔT时刻,即 该值中的增量与ΔT、τ呈反比关系,且τ越大极性反转后达到稳态所需时间亦越长。 1.2 非线性油纸绝缘的分析 1.2.1 非线性参数的选取及其影响的分析 目前,换流变压器广泛使用直流专用的KI50X变压器油,其击穿电压为88 kV/2.5 mm,含水率5 ppm以下,90℃时介质损耗因数小于0.001%,可有效地防止高压直流电场下的放电现象与功率损失。于会民、关健昕等人对KI50X变压器油及绝缘纸板在不同电场强度、不同温度下的电导率进行了大量的实验[11,20-21],数据如表1、表2所示。 表1 6 kV/mm时不同温度下2种材料的电导率Table 1 Two materials′ conductivity under different temperature at 6 kV/mm 表2 65 ℃时不同电场强度下KI50X油的电导率Table 2 Oil conductivity under different electric strength at 65 ℃ KI50X变压器油的电导率随电场强度或温度升高呈指数上升。绝缘纸板的电导率随温度升高呈指数上升但在电场强度小于50 kV/mm时并不随电场强度变化。对实验数据拟合得到KI50X变压器油及绝缘纸板的电导率的经验公式为: γ油=0.036 8e0.07Te0.8E+1×10-17S/m, γ纸=e0.05(T-75)×10-15S/m。 式中:T为温度;E为油中电场强度。 考虑到变压器油实际的工作环境,其电导率局部函数图像如图3所示。 如果不考虑电场强度对变压器油电导率的影响,由于温度的连续性,在油与纸板交界面处2种材料的温度相等,2种材料的电阻R1和R2为定值,仍可按照原数学模型进行计算与分析。 当考虑电导率的电场强度非线性时,R1和R2变为指数函数,此时无法通过求解一阶微分方程求得式(1)的解析解,本文采用Matlab 4阶Runge-Kutta算法进行数值求解,该方法用4阶方法提供候选解,5阶方法控制误差,是1种高精确度自适应步长的常微分方程数值解法。 图3 变压器油的电导率随电场强度、温度变化曲面Fig.3 Curved surfaces of oil conductivity changing with electric field intensity and temperature circuit 1.2.2 物理模型及数值计算 (3) 可知平行双极板中电压分布与两种介质的接触面积无关。由微分方程规律可知d1/d2的影响与线性方程时一致。由于实际工程中d1/d2≈1,故本文假设d1/d2=1,式(3)可简化为 根据实际工程数据,给定图1模型的参数为:ε0=8.85×10-12F/m,ε1=2.2,ε2=4.4,d1=d2=0.01 m,Um=105V,ΔT=60 s。应用Matlab进行数值计算得出20~105 ℃下油中电场强度E1(t)随时间(0 由图4可知:温度上升,非线性油中电场强度E1(0)与E1(6 000)均降低,且E1(6 000)趋近于E1(0),极性反转最大电场强度E1(6 000)在8.42~9.63 kV/mm之间变化并在65 ℃时达到极大值。由图5(a)、图6(a)可知:0 图4 0/60/6 000 s时非线性油中电场强度随温度变化曲线Fig.4 Curve of electric field intensity changing with temperature in oil at 0/60/6 000 s 图5 20 ℃时非线性油中电场强度、电压变化曲线Fig.5 Curve of electric field intensity and voltage changing with time in nonlinear oil at 20 ℃ 图6 105 ℃时非线性油中电场强度、电压变化曲线Fig.6 Curve of electric field intensity and voltage changing with time in nonlinear oil at 105 ℃ 表3 75 ℃线性与非线性油中电场强度对比Table 3 Comparing of electric field strength between linear and nonlinear oil at 75 ℃ 图7 75 ℃时线性油中电场强度、电压变化曲线Fig.7 Curve of electric field intensity and voltage changing with time in linear oil at 75 ℃ 由图7(a)可知:0 由表3可知:稳态时非线性油中的电场强度E1(0)为线性油中的36倍,极性反转时非线性油中的最大电场强度E1(60)为线性油中的78%。当t=6 000 s时线性油中的电压达到稳态,而非线性油中仍有18.3%的增量。线性油中的电场强度在极性反转时变化非常剧烈,最大电场强度为稳态时的144倍,而非线性油中仅为3.16倍。 换流变压器按照线性的情况设计会造成较大的裕度导致浪费。考虑非线性因素时,油纸绝缘的电场分布在极性反转后5 400 s时未达到稳态。 1.3 微观电荷量变化的分析 由于实际工程中R2C2>>R1C1,故有电荷积聚在油纸的界面处,且积聚电荷的极性与所施加电压的极性相同,国内外的大量实验[22-29]也验证了该理论。 当不考虑材料非线性时,τ′=[R1R2(C1+C2)]/(R1+R2)=τ。 由于R2>>R1,所以τ′可以近似变为R10×(C1C2),所以τ′与γ1呈反比关系,可以用1/τ′来表征界面上电荷的变化速度。 极性反转时界面处和极板上的电荷开始消散;由于稳态时油中电场强度较小,致使油中电导电流也较小,故位移电流占主要部分,认为极板上电荷的消散速度远大于界面处电荷的消散速度。极板上电压极性改变的瞬间,界面处积聚的电荷量变化非常小,随后极板上开始积聚相反极性的电荷,而界面处的电荷继续消散。随着电场强度上升,油中的电密开始增加,界面处电荷的消散速度亦开始增加,导致极性反转过程中油中的电场强度增加速度减慢,故极性反转完成时非线性油中的电场强度小于线性油中的电场强度。极性反转完成时极板上等效面电荷量达到稳态,界面上电荷继续消散直至为零,随后重新积聚与极板极性相同的电荷,油中电场强度逐渐降低;由于油的电导率随电场强度呈非线性变化,油中电密衰减速度也逐渐降低。 2.1 实例仿真 本文针对一台±400 kV换流变压器建立网侧和阀侧端部模型,使用ElecNet进行极性反转电压仿真,根据GB/T 18494.2计算其极性反转电压为 Upr=1.25[(N-0.5)Udm0.35Uvm]=460.73 kV。 其中:Uvm=178.8 kV为阀侧绕组最大相间交流工作电压;Udm=204 kV为每个阀桥最高直流电压;N=2为从直流线路中性点至与变压器相连的整流桥间所串接的六脉波桥的数量。 模型如图8所示,其中A、B为局部的网侧静电环和绕组,C、D为局部的阀侧静电环和绕组,E为压板,ab边为上铁箱壁,中间条状部分为绝缘纸板和角环,所有间隙均为变压器油。 图8 换流变压器网侧对阀侧端部模型Fig.8 Model of upper part of Line-valve side winding of convert transformer 按照实际情况添加曲率,设置A、B区域和ab边为接地边界条件,C、D区域所施加的极性反转电压如图9所示,其余边界为开放边界。 图9 模型电压Fig.9 Applied voltage on model 有限元剖分设置最大尺寸为2 mm,材料边缘加密25%,共计剖分105 337个三角形单元,三角形内采用线性插值,极性反转电压采用瞬态求解中的二阶Newton-Raphson非线性求解器,迭代次数为20次,许用公差为0.1%。为了简化计算,本文采用油道分段加温法进行仿真,网、阀侧各有5个油道,所施参数如表4所示。 2.2 仿真结果与分析 图10(a)表示0 s时,1—10号仿真的电场分布,且最大电场强度出现在阀侧第一油道静电环处,均为6.54 kV/mm。图10(b)代表5 460 s时,1—10号仿真的电场分布规律,且最大电场强度出现在阀侧第一油道静电环处,值见表5。图10(c)代表5 400 s时,1—6号仿真的电场分布规律,且最大电场强度出现在阀侧静电环上,值见表5。图10(d)表示5 400 s时,7号仿真的电场分布,且最大电场强度出现在阀侧第一油道静电环处,值见表5。图10(e)表示5 400 s时,8号仿真的电场分布,且最大电场强度出现在阀侧第一油道静电环处,值见表5。图10(f)代表5 400 s时,9—10号仿真的电场分布规律,且最大电场强度出现在网、阀侧静电环下尖端处,值见表5。 表4 换流变压器模型的温度参数Table 4 Temperature parameters of convert transformer model 温度升高有助于降低最大电场强度,但若阀侧温度高于网侧反而会增大阀侧出现的最大电场强度。20 ℃时变压器油与纸板的电导率降低了2个数量级,且变压器油与绝缘纸板的电导率之比由75 ℃的100∶1变为0.38∶0.01,故时间常数τ大幅度增加远大于5 400 s,因此5 400 s时油中电场强度仍然很高。5 460 s时油中最大电场强度由12.03 kV/mm降低至7.91 kV/mm。当考虑电场强度非线性、温度为75 ℃时,5 460 s时最大电场强度由12.03 kV/mm降至76%即9.15 kV/mm,与Matlab的仿真结果相符,而5 400 s时油中的电场强度与纸板中的电场强度相近。存在温度梯度时若考虑电场强度非线性则油中的电场强度在3.4~4.1 kV/mm范围变化,不考虑电场强度非线性时在0.002~0.02 kV/mm范围变化,故变压器油电导率的电场强度非线性会均化由温度梯度带来的电场强度梯度。 表5 5 400/5 460 s时最大电场强度Table 5 Maximum electric field strength at 5 400/5 460 s 图10 电场分布图Fig.10 Distribution of electric field 绝缘纸板的许用场强为40 kV/mm,长时直流电压下变压器油的许用场强为10 kV/mm、极性反转电压下变压器油的许用场强为13 kV/mm。由仿真结果可知:绝缘纸板在所有情况下均有很大的绝缘裕度。当不考虑材料的非线性时,5 400 s和5 460 s时变压器油的绝缘裕度分别为500和1.08;当考虑材料的非线性时,5 400 s和5 460 s时变压器油的绝缘裕度分别为2.44和1.42。故5 400 s时变压器油并没有很大的绝缘裕度,5 460 s时变压器油的绝缘裕度反而增大。 1)非线性材料极性反转完成时油中的最大电场强度为线性材料的78%; 2)温度越低电场达到稳态所需时间越长、极性反转时油中的最大电场强度越低、极性反转完成后油中的电场强度越高; 3)电导率的电场强度非线性会均化由温度梯度带来的电场强度梯度; 4)通过加厚纸板和增大静电环曲率半径均可以降低油中电场强度。 [1] 赵畹君.高压直流输电工程技术[M].北京:中国电力出版社,2004:60-65. [2] ELLIOTT FE,LAVIER BE,KUEHN WP,et al.FEM-study on converter transformer failures in the Celilo HVDC converter station[J].PESW,1999:1047. [3] HP Moser.Transformerboard II[M].Germany:Zürich,1999:53. [4] 李晓黎,陈祖胜.特高压直流输电技术发展综述[J].广西电力,2009(1):23. LI Xiaoli,CHEN Zusheng.Summary of ultrahigh voltage direct current transmission technology[J].Guangxi Electric Power,2009(1):23. [5] 李文平,陈志伟,宋秀生,等.±800 kV直流输电工程用换流变压器主绝缘结构的研究[J].电力设备,2007,8(3):5. LI Wenping,CHEN Zhiwei,SONG Xiusheng,et al.Analysis on main insulation structure of converter transformer for ±800 kV HVDC transmission[J].Electrical Equipment,2007,3(8):5. [6] TAKAHASHIE,SHIRASAKA Y,OKUYAMA K.Analysis of an anisotropic nonlinear electric field with a discussion of dielectric tests for converter transformers and smoothing reactors[J].IEEE Transactions on Power Delivery,1994,9(3):1480. [7] RONGSHENGL,WAHLSTROM G.Measurements of the DC electric field in liquid impregnated pressboard using the pressure wave propagation technique[C].Australia:Brisbane,1994:103-106. [8] LI Jinbiao,XIE Dexin,WANG Xiaoyan.Adaptive FE analysis of nonlinear and anisotropic DC electric field of converter transformer in HVDC transmission systems[C].Automation Congress,2008.WAC 2008.World.2008. [9] 张施令,彭宗仁,冯骅.复合绝缘非线性电场的有限元迭代计算[J].电网技术,2014,38(2):448. ZHANG Shiling,PENG Zongren,FENG Hua.Iterative finite element method applied to nonlinear electric field of composite insulation.power system technology[J].Power System Technology,2014,2(38):448. [10] 刘刚,李琳,李文平,等.换流变压器极性反转非线性电场分析[J].高电压技术,2012,38(2):451. LIU Gang,LI Lin,LI Wenping,et al.Analysis of nonlinear electric field of converter transformer under polarity reversal voltage[J].High Voltage Engineering,2012,2(38):451. [11] 关健昕.油纸绝缘电导非线性特性对阀侧出线绝缘裕度的影响研究[D].北京:中国电力科学研究院,2014. [12] WENKC,ZHOU YB,FU J,et al.A calculation method and some features of transient field under polarity reversal voltage in HVDC insualtion[J].IEEE Transactions on Power Delivery,1993,8(1):223. [13] 王冰,王清璞,孙优良.换流变压器阀侧绕组端部极性反转瞬态电场的计算与分析[J].变压器,2007,44(6):11. WANG Bing,WANG Qingpu,SUN Youliang.Calculation and analysis of polarity reverse transient electric field in valve winding end of converter transformer[J].Transformer,2007,44(6):11. [15] 王永红,魏新劳,朱宝森,等.极性反转电压下变压器油的击穿特性[J].电机与控制学报,2011,15(3):46. WANG Yonghong,WEI Xinlao,ZHU Baosen,et al.Breakdown characteristics of transformer oil at DC polarity reversal voltage[J].Electric Machines and Control,2011,15(3):46. [16] 王永红,魏新劳.极性反转电压下油纸复合绝缘的特性[J].中国电机工程学报,2012,32(19):161. WANG Yonghong,WEI Xinlao.Characteristics of oi-pressboard insulation under polarity reversal voltage[J].Proceedings of the CSEE,2012,32(19):161. [17] 魏新劳,聂洪岩,陈庆国,等.极性反转电压下油纸绝缘系统中电场分布[J].电机与控制学报,2010,14(11):27. WEI Xinlao,NIE Hongyan,CHEN Qingguo,et al.Analysis of electrical field on oil-paper insulation system under polarity reversal voltage[J].Electric Machines and Control,2010,14(11):27. [18] 丁中尼,李光范.极性反转时典型油纸复合绝缘的电场特性[J].电网技术,2008,32(23):82. DING Zhongni,LI Guangfan.Electric field characteristic calcul-ation on typical oil-paper combination insulation under polarity reversal[J].Power System Technology,2008,32(23):82. [19] 吕晓德,陈敦利.极性反转时换流变压器绝缘电场特性研究[J].高电压技术,1997,23(1):67. LÜ Xiaode,CHEN Dunli.The study on electric field characteristics of converter transformer under polarity reversal[J].High Voltage Engineering,1997,23(1):67. [20] 聂洪岩.极性反转电压作用下油纸复合绝缘系统击穿特性研究[D].哈尔滨:哈尔滨理工大学,2010. [21] 于会民,张绮,郭春梅,等.KI150X和KI150GX变压器油的应用研究[J].润滑油,2012,27(3):21. YU Huimin,ZHANG Qi,GUO Chunmei,et al.Application study on KI150X and KI150GX Transformer Oils[J].Lubricating Oil,2012,27(3):21. [22] 于会民,郑鹏宇,张培恒,等.高压直流电场下UHV换流变压器用油电导率的对比研究[J].绝缘材料,2014,47(5):96. YUHuimin,ZHENG Pengyu,ZHANG Peiheng,et al.Condu-ctivity comparative study of transformer oils for uhv converter transformer in HVDC electric field[J].Insulating Materials,2014,47(5):96. [23] KATOK,OKUBO H,ENDO F,et al.Investigation of charge behavior in low viscosity silicone liquid by Kerr electro-optic field measurement[J].IEEE Transactions on Dielectrics and Electrical Insulation,2010,17(4):1214. [24] OKUBOH,SHIMIZU R,SAWADA A,et al.Keer electro-optic field measurememt and charge dynamics in transformer oil/solid composite insulation systems[J].IEEE Transactions on Dielectrics and Electrical Insulation,1997,4(1):64. [25] CHEN George.Research on the feature extraction of DC space charge behavior of oil-paper insulation[J].Science China(Technological Sciences),2011(5):1315. [26] CIOBANU R,SCHREINER C,PFEIFFER W,et al.Space charge evolution in oil-paper insulation for DC cables application[C].Austria:Graz,IEEE,2002:321-324. [27] 周远翔,田冀焕,王云杉,等.变压器油纸绝缘系统中的空间电荷现象[J].高电压技术,2011,37(3):520. ZHOU Yuanxiang,TIAN Jihuan,WANG Yunshan,et al.Analysis of electrical field on oil-paper insulation system under polarity reversal voltage[J].High Voltage Engineering,2011,37(3):520. [28] 张明泽,赵东旭,黄玲,等.变压器油纸绝缘含水量的介电响应测量方法[J].哈尔滨理工大学学报,2016,21(2):84. ZHANG Mingze,ZHAO Dongxu,HUANG Ling,et al.Dielectric response measuring method on moisture content of oil-paper insulation in transformer[J].Journal of Harbin University of Science and Technology,2016,21(2):84. [29] 王正伟,赵大伟,杨嘉祥,等.阶跃电压下液体电介质击穿过程数值分析[J].哈尔滨理工大学学报,2014,19(3):80. WANG Zhengwei,ZHAO Dawei,YANG Jiaxiang,et al.Numerical analysis of liquid dielectric breakdown process applied in step voltage[J].Journal of Harbin University of Science and Technology,2014,19(3):80. [30] 张秋也,朱学成,高自伟,等.温度对油、纸介电参数及复合电场分布的影响[J].哈尔滨理工大学学报,2015,20(6):59. ZHANG Qiuye,ZHU Xuecheng,GAO Ziwei,et al.Influence of temperature on dielectric parameters of oil & pressboardand the electric field distribution of oil-paper insulation under compound voltage[J].Journal of Harbin University of Science and Technology,2015,20(6):59. (编辑:张 楠) AnalysisoflinearandnonlinearelectricfieldofHVDCconverttransformeroil-boardinsulation LIU Wen-li1,BAI Shi-guang2,LI Yi-chun3,LI Jia-xin4 (1.School of Electrical and Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China;2.Datang Northeast Electric Power Test & Research Institute,Changchun 130015,China;3.East Inner Mongolia Electric Power Company,Hohhot 010000,China;4.East Inner Mongolia Electric Power Company,Tongliao 028000,China) Converter transformer oil-board insulating material′s conductivity changes nonlinearly with electric field intensity and temperature.This nonlinear change rule is data-fitted in order to study the influences of material′s nonlinearity to the distribution of converter transformer polarity reversal electric field.Calculation and analysis were carried out using RC equivalent circuit.The upper part of line and valve side windings’ electric field of one ±400 kV converter transformer were simulated by using the finite element software ElecNet.The results show that while the polarity reversal finishes,the maximum field strength of nonlinear material is of 78% compared with linear material.While at steady state,the field strength in the nonlinear oil is 36 times of linear oil.The conductivity change caused by electric field would homogenize the the electric field gradient caused by the temperature gradient.Finally,a few improvement measures are offered according to calculation and simulation results. converter transformer;electric field distribution;polarity reversal;oil-board insulation;nonlinear material 10.15938/j.emc.2017.09.011 TM 401 :A :1007-449X(2017)09-0080-08 2015-06-18 国家自然科学基金(51207037) 刘文里(1956—),男,硕士,教授,研究方向为变压器的理论研究、结构设计与计算;白仕光(1991—),男,硕士,研究方向为变压器电、磁场计算与分析;李祎春(1990—),男,硕士,研究方向为变压器电、磁场计算与分析;李佳欣(1990—),女,硕士,研究方向为变压器电、磁场计算与分析。 白仕光
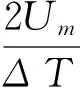



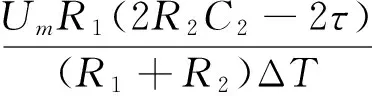






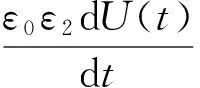







2 实例分析




3 结 论

