变速变负载无轴承永磁同步发电机悬浮力及发电性能研究
刁小燕,胡亚民,朱熀秋,陆荣华,黄建波
(江苏大学 电气信息工程学院,江苏 镇江 212013)
变速变负载无轴承永磁同步发电机悬浮力及发电性能研究
刁小燕,胡亚民,朱熀秋,陆荣华,黄建波
(江苏大学 电气信息工程学院,江苏 镇江 212013)
针对普通发电机轴承磨损严重的问题,提出一种无轴承永磁同步发电机。首先分析了无轴承永磁同步发电机的悬浮原理和发电原理;其次,推导了感应电压表达式,利用麦克斯韦张量法建立悬浮力和电磁转矩的数学模型并验证其正确性;再次,运用参数化分析法设计并优化了发电机结构,仿真结果验证了发电机具有良好的悬浮力和电磁性能;另外,将设计的样机进行试验,验证了该发电机具有良好的动态性能;最后针对发电机常见的变速、变负载的问题,基于有限元仿真分析了其对发电机运行性能的影响。仿真结果说明该发电机在特殊工况下具有良好的悬浮性能。研究表明提出的新型发电机具有良好的动静态性能可以稳定运行。
无轴承永磁同步发电机;数学模型;变负载;变转速;性能分析
0 引 言
永磁同步发电机具有结构简单、效率高、功率密度大、拓扑结构灵活多样、无需电刷结构、运行可靠等诸多优点。在风力发电机、燃气轮发电机、航空电源、混合动力汽车、飞轮储能系统电动/发电一体机等诸多场合的应用日益广泛[1],这对发电机运行的可靠性提出了更高的要求。由于发电机工作环境复杂多变,容易引发其定子、转子、轴承等部件的一系列电气或机械故障,据相关数据统计,其中轴承故障高达40%左右[2]。为了削弱轴承故障的影响,延长发电机的轴承使用寿命,本文提出一种永磁同步无轴承化的发电机(bearingless permanent magnet synchronous generator,BPMSG)。与传统的永磁同步发电机(permanent magnet synchronous generator,PMSG)相比,BPMSG具有无摩擦、无接触、无需润滑和维护费用低等优点[3-4]。
目前,国内外的研究热点主要集中在无轴承永磁同步电机的电动状态[5-6]。由于永磁同步电机起动和发电性能的优越性,发电运行状态的BPMSG作为无轴承永磁同步电机的另一种工作模式的研究正处于前期探索阶段,并将成为新的研究热点。BPMSG高速运行时转轴与辅助轴承无机械接触,有效解决了高速电机轴承磨损发热的问题,因此适用于轴承难以更换的深海、航空领域。就结构而言,本文提出的BPMSG在普通的PMSG的定子上叠绕了一套悬浮力绕组。原本的转矩绕组作为发电绕组,基于电磁感应定律感应发电。由于其控制策略和数学模型均比PMSG复杂,因此不能将PMSG的控制分析方法完全运用到BPMSG上[7]。
为此,本文结合普通PMSG和无轴承电机的运行状态,提出了一种无轴承永磁同步发电机。首先分析了BPMSG的悬浮原理和发电原理;其次推导了发电机的感应电压表达式,建立悬浮力和电磁转矩的数学模型;再次基于有限元仿真和参数化分析设计了发电机的结构参数,通过仿真实验验证数学模型的正确性和该BPMSG具有良好的发电和悬浮性能;另外,将设计的样机进行试验,验证了该BPMSG具有良好的动态性能;最后模拟在变负载、变转速情况下,分析BPMSG的运行性能,结果验证了BPMSG在特殊工况下具有良好的悬浮性能。
1 BPMSG悬浮原理和发电原理
1.1 绕组结构和悬浮原理
图1为BPMSG的绕组结构和悬浮原理结构示意图。为得到稳定的悬浮力和较小的转矩波动,采用表贴式转子、36槽分布式绕组的定子结构,悬浮力绕组每极每相槽数为6,转矩绕组每极每相槽数为3,均为整数槽结构。为了产生可控的径向悬浮力[8],需满足:
(1)
其中:PG和ωG分别是发电绕组极对数和电流角频率;PB和ωB分别是悬浮力绕组极对数和电流角频率。转子永磁体和发电绕组采用2对极,悬浮力绕组采用1对极。转子在径向上一般受到两种电磁力:麦克斯韦力和洛伦兹力。

图1 无轴承永磁同步发电机的绕组结构Fig.1 Winding structure of BPMSG
以a相为例,定子槽中缠绕着4极发电绕组Nga,与2极悬浮力绕组Nsa。当悬浮力绕组Nsa中未通入电流时,发电绕组产生感应磁场与永磁体合成的4极气隙磁通φm是平衡的,将不会产生径向力;当Nsa中通入正电流后,将会产生2极磁通φα,导致转子左侧气隙2处磁密增加,转子右侧气隙处磁密减小,从而产生沿x轴负方向的麦克斯韦力,使转子向x轴负方向偏移;如果通以相反方向的电流,则会产生一个沿x轴正方向的麦克斯韦力。同理,沿y轴方向的麦克斯韦力可以通过在其他绕组中通入相应电流获得。
无轴承永磁同步电机除了受麦克斯韦径向力之外,还会受到洛伦兹径向力的作用。图1中标于绕组上的力为悬浮力绕组和发电绕组所受到的洛伦兹力,表贴式转子表面上对应的力为其反作用力。可以看出,这两部分洛伦兹力的合力方向为水平方向,即转子受到了x轴方向的径向悬浮力。可以证明,通过控制两套绕组电流之间的相位差可以产生任意方向上的悬浮力,此闭环控制可实现发电机转子的悬浮。
1.2 BPMSG的发电原理
BPMSG在发电过程中一般面临变转速、变负载的问题,需要电力电子技术对其进行稳压恒频。三相不可控整流电路由于交流侧会产生较大的谐波,会引起发热和永磁体退磁等一系列问题。如图2所示,应用PWM整流电路能有效解决上述问题[9-10]。该BPMSG的发电绕组外接PWM整流电路向负载供电。PWM整流电路可以将感应到的频率不稳定的交流电流转换成便于贮存和转化的直流电。PWM整流系统不仅能够实现直流侧电压的调节,也能提高交流侧发电机的功率因数、降低发电机电流的谐波。同时发电绕组磁链将随转子位置角的变化而变化,使得发电绕组线圈中产生感应电动势,绕组形成回路产生感应电流,负载两端形成电压,如图3所示。
由于转子永磁体的极对数和悬浮力绕组的极对数不同,当没有转子偏心时,永磁体在悬浮力绕组中不产生感应电流,悬浮力绕组电流也不会产生转矩,即BPMSG的悬浮力控制与发电控制是自然解耦的[8]。
2 建立BPMSG的数学模型
BPMSG是一个非线性、强耦合、多变量的系统。要获得高动态性能,必须建立准确的动态模型。为了建立BPMSG的d-q轴数学模型,首先进行如下假设:1)假设发电机的磁路是线性的;2)不计铁心饱和与漏感;3)忽略涡流和磁滞损耗;4)假设气隙磁场呈正弦分布;5)假设转子上没有阻尼绕组。
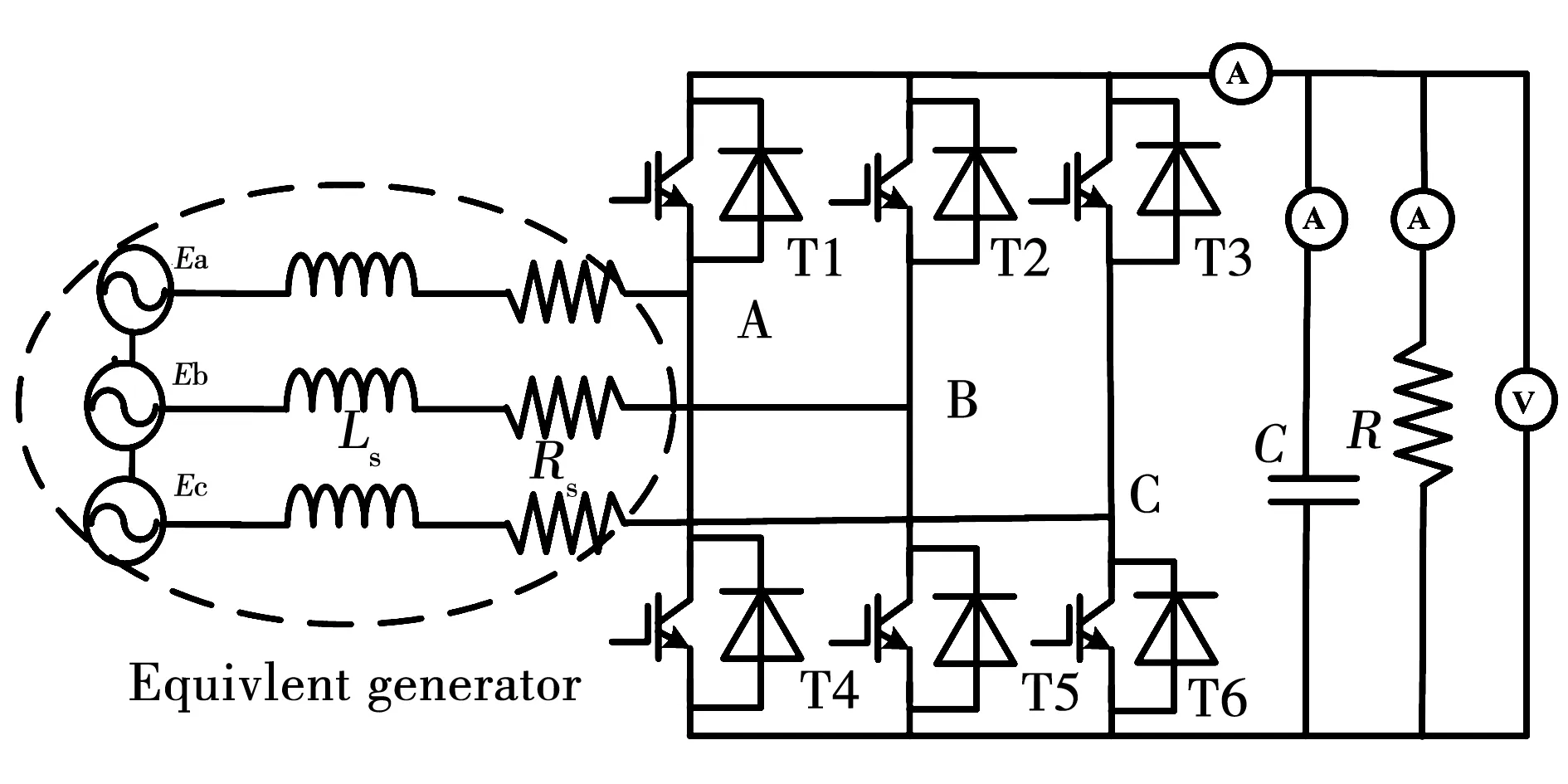
图2 BPMSG-PWM整流电路Fig.2 Rectifier circuit of BPMSG-PWM

图3 整流电路负载电流电压Fig.3 Load current and voltage of rectifier circuit
2.1 感应电压数学模型
BPMSG的三相磁链方程可写为
(2)
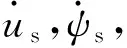
本模型所研究的是表贴式发电机,转子磁链呈正弦分布。若A相定子绕组与a相转子轴线之间的电角度为θr,则θr=ωrt+θ0。式中:ωr是转子电角速度(rad/s);θ0是A相定子绕组与转子轴线之间初始角度(rad)。由于三相对称电流满足ia+ib+ic=0,令等效电感Ls=L-M,可得:
(3)
由上式可知,BPMSG在三相坐标系下的数学模型可以等效为三相星形连接的对称电路,且每相电压都由反电势、电感和电阻上面的电压三部分构成。
2.2 悬浮力的数学模型
根据BPMSG原理,气隙磁场是由发电绕组,永磁转子和悬浮力绕组产生的磁场相互作用产生。三者产生的磁动势基波分量分别为:
(4)
式中:F1m,Ffm,F2m分别为发电绕组、永磁转子和悬浮力绕组产生的气隙磁动势基波幅值;φ为气隙中任意处与x轴的夹角;λ1,μ1,μf为电机气隙中各个气隙磁动势基波对应的初始相位角;ω为发电绕组和悬浮力绕组电流的电角频率;pG、pB分别为发电绕组和悬浮力绕组极对数。由于发电绕组和永磁转子所产生的磁场都是pG对极,两者共同建立的合成气隙磁动势基波为
f1f(φ,t)=f1(φ,t)+ff(φ,t)=
F1fcos(ωt-pGφ-μ1)+
Ffmcos(ωt-pGφ-μf)。
(5)
这样BPMSG气隙中只存在两种磁动势:发电绕组和永磁体合成的磁动势与悬浮力绕组产生的磁动势。由于定子铁心和转子铁心的相对磁导率远大于空气的相对磁导率,故定、转子铁心的磁阻可以忽略。通过计算可知气隙磁通密度为
B12f(φ,t)=B1f(φ,t)+B2(φ,t)=

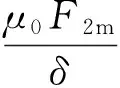
(6)
转子不偏心时δ=δ0。当转子出现偏心时,由图4可知,气隙中磁通密度B不再均匀。e表示偏心位移,任意方向上的气隙长度为
δ(φ)=δ0-ecos(φ-φs)。

图4 转子偏心定义Fig.4 Definition of rotor eccentricity
根据麦克斯韦张量法,转子表面沿电气角度φ处ds面积上受到的径向力悬浮力可表示为
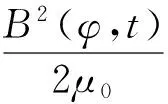
(7)
对于pG=2,pB=1的BPMSG,将上式对变量φ在0~2π上进行积分,化简可得:
(8)
式中:kd1和kd2分别表示发电绕组和悬浮力绕组的基波绕组系数;N1和N2表示发电绕组和悬浮力绕组每相串联匝数[8]。
从上式可以看出,BPMSG转子径向上主要受到两种作用力。均匀气隙中pG、pB对极气隙磁场相互作用产生的可控悬浮力,其大小与悬浮力绕组的电流大小成正比,与转子偏心量无关;转子偏心后,发电机气隙长度分布不均,不对称的气隙磁场分布在转子上产生了单边磁拉力。其大小与偏心距、pG对极磁场气隙磁通密度的平方成正比。
2.3 电磁转矩数学模型
对于BPMSG来说,电磁转矩是克服原动机带动旋转的转矩,为制动性质的转矩。由电机能量转换原理,得到BPMSG转矩表达式(9)。可以看出,主要是电磁转矩由永磁转子和发电绕组之间的磁场相互作用。由于BPMSG是表贴式的,d-q轴分量发电绕组电感近似等于Ld=Lq,电磁转矩的数学公式的形式可以参考[11]传统PMSG,即
Te=PGψ1dI1q+PG(Ld-Lq)I1dI1q=PGψ1dI1q。
(9)
式中:ψ1d=ψGd+ψfd,ψ1q=ψGq+ψfq,ψ1d和ψ1q分别是d-q轴等效发电绕组气隙磁链分量;ψGd和ψGq分别是d-q轴发电绕组气隙磁链分量;ψfd和ψfq分别是d-q轴永磁体激发的气隙磁链分量。
3 BPMSG设计及仿真分析
3.1 基于参数化分析的主体尺寸设计
在发电机设计初期,电机的几何尺寸、绕组匝数、线规等参数是无法准确给出的,需要经过反复计算、多方案对比后才能确定相关参数,该过程就是电机中的参数化分析和优化设计。为得到合理的发电机模型,在Maxwell2D中以定子长度为例,进行参数化分析。
表1中L为定子轴向长度;Faverage为悬浮力的平均值;Ferror为悬浮力的波动,用悬浮力峰峰值表示;Taverage为转矩的平均值;Terror为转矩波动。由于此模型为发电机,该转矩为制动状态的转矩,所以为负值。

表1 电机定子轴向长度变化情况Table 1 Changes of motor stator axial length
从图5中可以直观地看出当定子轴向长度为50 mm时,转矩平均值的绝对值最大且最稳定。悬浮力的值随着定子轴向长度的增大而增大,但只有在50 mm处的波动最小,即悬浮力最稳定。由上例,基于Ansoft软件对定转子尺寸、悬浮力电流、永磁体厚度,定子槽数、气隙宽度等的参数化分析,可以得到较为合理的发电机参数。取发电机的额定转速为1 500 r/min,定子槽满率为0.75,悬浮力绕组电流幅值取3 A。根据参数化分析得到的最优尺寸,如表2所示。
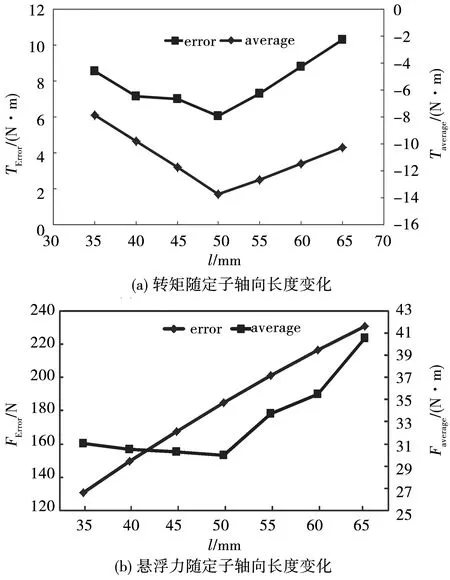
图5 定子轴向长度参数化分析Fig.5 Parametric analysis of the stator axial length
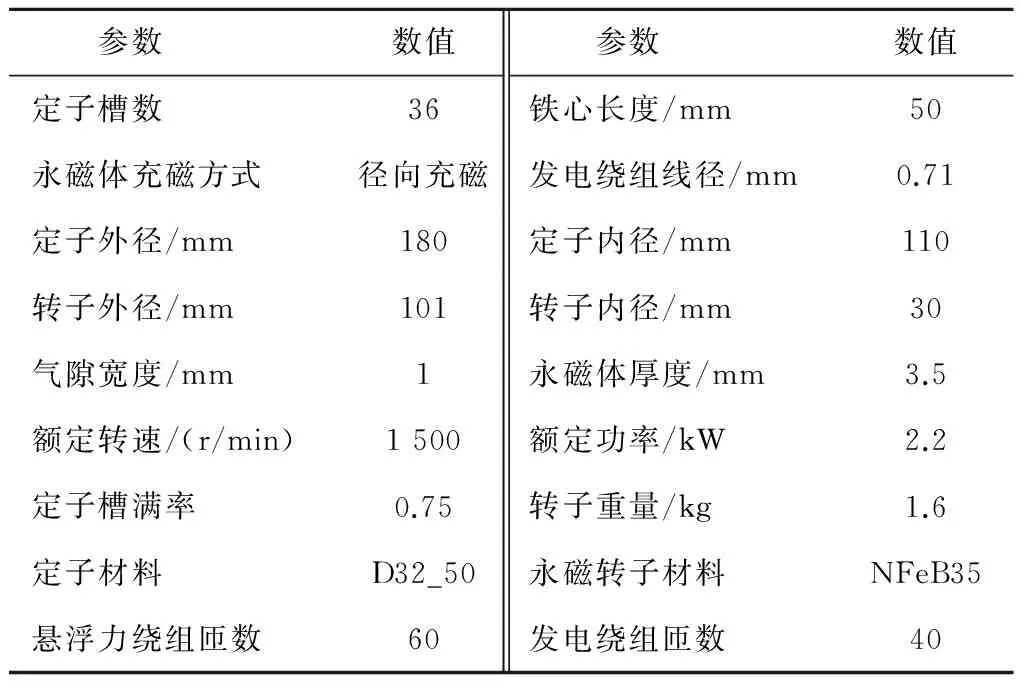
表2 样机结构参数Table 2 Structural parameters of the prototype
代入参数化分析设计的电机尺寸,可以验证第2节中推导的数学模型。以径向悬浮力与悬浮力绕组电流幅值为例,如图6所示,在转子不偏心的情况下:当悬浮力电流幅值小于3 A时,随着悬浮力电流的增加,转子所受的径向悬浮力呈线性逐渐增加,验证了模型的正确性;但当悬浮力电流幅值大于3 A时,由于铁心饱和的影响,悬浮力增加越来越缓慢,出现了严重的非线性。
转子不偏心时悬浮力的角度为128°。在模型中设置转子的位置使其偏心于相反方向,即-52°,则转子受到的单边磁拉力与可控悬浮力方向相反。当悬浮力电流幅值很小时,径向悬浮力中起主要作用的是单边磁拉力。随着电流的增大,可控悬浮力逐渐增大,在某一时刻会出现可控悬浮力的幅值等于单边磁拉力的情况。两个力相平衡,此时转子受到的径向力为零,过了这平衡点之后,可控悬浮力持续增大且占据主要部分,使合成悬浮力趋于线性增加。同样在电流增大到一定程度,会出现磁场饱和的趋势。综上,从仿真波形和计算结果的对比分析,可以验证推导的数学模型是正确的。

图6 径向悬浮力与悬浮力绕组电流幅值的关系Fig.6 Relationship between radial levitation force and levitation force winding current amplitude
3.2 BPMSG发电及悬浮力性能仿真与分析
根据表2的样机结构参数,利用时步有限元法对设计的样机进行瞬态有限元仿真[12],图7是样机的有限元模型。发电绕组外接图2所示的整流负载电路,观察在恒转速、恒负载下发电机发电绕组感应电流、悬浮力、以及发电电压的波形。

图7 无轴承永磁同步发电机有限元模型Fig.7 Finite element model of BPMSG

图8 BPMSG发电状态下电磁及悬浮力性能Fig.8 Electromagnetic and levitation force performance of BPMSG under the Power state
在原动机拖动BPMSG工作时,由于负载中存在电容、电感等储能元件。在刚进入工作状态时,这些储能元件会处于充电过程,会对负载电流有所影响,如图8(a)所示。发电绕组电流的不稳定还会影响电枢反应磁场,造成悬浮力在充电过程中略有波动,如图8(c)所示。待充电过程结束后悬浮力和感应电流都趋于稳定。图8(b)为仿真的发电电压波形。由发电电压波形可知,电压上升很快,并迅速趋于稳定,其稳态值为125 V左右。仿真中采用开环方式对发电电压进行控制,稳态时发电电压有少许波动。如果对发电电压采用闭环控制策略,迅速调节输出电压,可以进一步提高发电电压品质,这是今后的研究重点。
3.3 BPMSG实验结果分析
将提出的2.2 kW的BPMSG进行实验验证,样机参数见表2。实验采用TMS320F2812DSP作为控制器构建数字控制系统。

图9 BPMSG实验波形Fig.9 Experimental waveforms of BPMSG
图9(a)是n=1 500 r/min时转子径向偏心位移轨迹图。根据“陀螺效应”,旋转物体速度越快,物体越容易达到稳定状态。从图中可以看出,在α轴方向上,永磁薄片转子偏心位移最终稳定在-60~60 μm之间;在β轴方向上,永磁薄片转子偏心位移最终稳定在-80~80 μm之间。图9(b)是转速n=1 500 r/min时电机两套绕组的A相电流波形。由图可以看出,发电绕组电流呈现较好的正弦或余弦状。由于永磁薄片转子在运行过程中其径向偏心位移具有不可预知性,偏心位移的大小和方向都不能确定,为了使转子能够回复到平衡位置,转子所受到的径向悬浮力必须要根据转子偏心位移的方向和大小作相应的实时改变,这样悬浮力绕组电流的幅值和相位就必须根据所需径向悬浮力的大小和方向作出相应不可预知的改变,即呈现非标准正弦或余弦状。图9(c)是发电电压波形。以上实验结果表明:该BPMSG转子动态稳定悬浮,发电系统具有良好的动态性能。
4 特殊运行状态BPMSG性能分析
4.1 变负载情况下BPMSG性能分析
在日常生活中,发电机产生的电能一般用来供给生产生活设备用电。而这类用电设备种类繁杂,且投切频繁,这就必须考虑负载变化的情况。当负载变化时,发电绕组感应电流及负载电压电流势必发生变化,这就需要电力电子技术进行稳压恒频,这与普通永磁同步发电机无异[13]。

图10 压控开关管控制的BPMSG-PWM整流电路Fig.10 BPMSG-PWM rectifier circuit controlled by voltage-controlled switch tube
为验证BPMSG的悬浮力与负载变化的关系,对电机处于不同负载状态下的悬浮力进行仿真分析[14]。如图10所示,在发电绕组外接电路的整流桥和负载之间加一个压控开关管,该压控开关管由压控开关管模型元件和脉冲电压信号元件共同控制的。当脉冲电压信号为1时,压控开关管闭合,此时工作在加负载发电运行状态;当脉冲电压信号为0时,压控开关管断开,等效于空载发电运行。由于此BPMSG额定转速为1 500 r/min,触发脉冲的时间要超过一个周期,设为30 ms,即30 ms前发电机工作在加负载状态,30 ms后工作在空载状态。由图11可以看出,悬浮力的分力在XY方向有很大程度上的减小,而悬浮力的合力只是轻微降低。也就是说负载变化对悬浮力性能影响不大,悬浮力的值稳定在180 N附近。

图11 不同负载状态下的悬浮力Fig.11 Levitation force under different load
4.2 变转速情况下BPMSG性能分析
实际工业生产生活应用中,原动机的转速不可能保持绝对恒定。以风力发电机为例,风速的变化是随机的[13-14]。
在3.2节中,原动机保持额定转速时,有限元仿真中悬浮绕组的电流给定以时间作为变量。考虑到现在转速发生变化时,由公式ω=πnp/30可知,会导致悬浮力绕组外加的电流频率发生相应的变化。故将悬浮绕组通入的电流改成由转子位置γ作为变量的三相交流电,如下式所示:
(10)
因为转速的变化,转子每次扫过相同角度的时间就随之改变,即通过改变的相位间接表现为控制电流频率的变化。为模拟转速的渐变与突变,在有限元仿真软件中将拖动BPMSG的原动机的给定转速设置成1 500+100×sin(100πt)+100×sgn(sin(100πt))。该函数描述了发电机在转速差为0~400 r/min时的转速波形。如图12所示,在0~10 ms,正弦函数可以模拟转速的大小渐变。在10 ms时,符号函数模拟转速的突变。

图12 无轴承永磁同步发电机转速波动Fig.12 Speed fluctuation of BPMSG
如图13所示,当转速变化的时候,XY方向上的悬浮力平均值大小发生明显变化。转速波动时Y方向的分力产生波动,且具有相同的正弦振荡趋势,而X方向分力基本保持稳定,悬浮力合力的大小依然维持在180 N附近;但发电绕组的感应电流以及负载的电流电压却受较大的影响。如何得到频率恒定,大小稳定的电流,这需要设置闭环控制环节配合整流逆变技术来解决问题。
该发电机额定转速是1 500 r/min,考虑实际转速变化的随机性,图12中转速的波动幅度为400 r/min,并不具有代表性。理论上分析,随着转速变化加剧,发电绕组中感应电流变化明显,将会影响气隙磁场,进而影响悬浮力大小。将BPMSG的原动机给定转速设置成函数1 500+range×sgn(sin(100πt))+range×sin(100πt),其中变量range的取值范围为0~500 r/min。表3列举出转速波动幅度0~2 000 r/min时,平均悬浮力大小的值。图14描述的是0~2 000 r/min时悬浮力的波形,可以看出,随着转速波动加强,悬浮力的稳定性变差,悬浮力平均值也相应减小,但依然能使电机悬浮。说明在一定范围内的转速波动下,BPMSG能保持稳定运行。

表3 不同转速波动幅度下平均悬浮力大小Table 3 Suspension force of different speed fluctuation
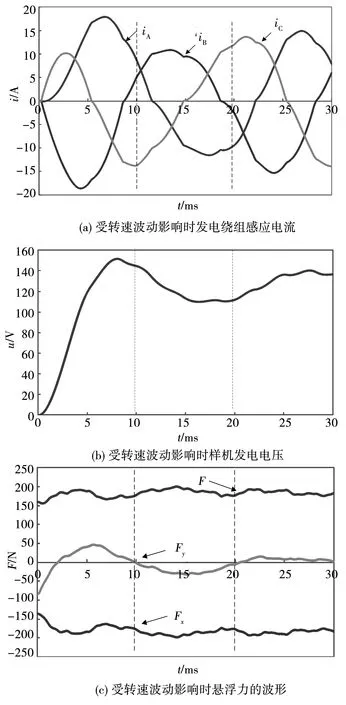
图13 BPMSG变转速下电磁及悬浮力性能Fig.13 Electromagnetic and levitation force performance of BPMSG under variable speed

图14 不同转速波动幅度下的悬浮力Fig.14 Suspension force of different speed fluctuation
5 结 论
本文设计了36槽分布绕组结构的BPMSG。在分析其悬浮原理和发电机理的基础上,研究了BPMSG的各项性能指标,得到如下结论:
1)BPMSG可控悬浮力大小与悬浮力绕组电流大小成正比,单边磁拉力大小与偏心距、pG对极磁场气隙磁通密度的平方成正比。
2)运用参数化分析对发电机结构性能进行优化,选择恰当参数构建BPMSG样机模型,仿真结果准确反映了该发电机具良好的悬浮性能和发电品质,同时也验证了数学模型的正确性。
3)模拟了BPMSG在负载发生变化和原动机牵拉的转速发生波动,两种特殊工况下的悬浮力及发电性能。结果显示该发电机在特殊工况下悬浮力虽然会有轻微波动,但发电机仍然正常运行。
4)由于感应电流的变化会影响合成磁场,变负载变转速工况对发电性能影响较大。为了提高发电机发电品质,拟采用转子混合励磁结构,并对主磁场进行闭环控制。
[1] 李伟力,程鹏,吴振兴,等.并网永磁同步发电机转子永磁体局部失磁特征量的计算与分析[J].中国电机工程学报,2013,33(33):95. LI Weili,CHENG Peng,WU Zhenxing,et al.Calculation and analysis on the permanent magnet partial demagnetization characteristics of the grid-connected permanent magnet synchronous generator rotor [J].Proceedings of the CSEE,2013,33(33):95.
[2] 孙斌,王艳武,杨立.基于红外测温的异步电机轴承故障诊断[J].电机与控制学报,2012,16(1):50.SUN Bin,WANG Yanwu,YANG Li.Study of fault diagnosis of induction motor bearing based on infrared inspection[J].Electric Machines and Control,2012,16(1):50.
[3] 周云红,孙玉坤.一种双定子型的磁悬浮开关磁阻双通道全周期发电机[J].中国电机工程学报,2015,35(9):2295.ZHOU Yunhong,SUN Yukun.A double-stator type bearingless switched reluctance dual-channel full-period generator[J].Proceedings of the CSEE,2015,35(9):2295.
[4] 周云红,孙玉坤,嵇小辅.一种新型的磁悬浮开关磁阻发电机[J].中国电机工程学报,2012,32(15):107.ZHOU Yunhong,SUN Yukun,JI Xiaofu,et al.A novel bearingless switched reluctance generator[J].Proceedings of the CSEE,2012,32(15):107.
[5] Chinchilla M,Arnaltes S,Burgos J C.Control of permanent-magnet generators applied to variable speed wind-energy systems connected to the grid [J].IEEE Transactions on Energy Conversion,2006,21(1):130.
[6] STEFANI F,PENNATINI A,CEFALO A.AC series voltage regulator for permanent magnet generators[C]//Proceedings of IEEE International Symposium on Research in Microelectronics and Electronics,2009:92-95.
[7] 曹鑫,邓智泉,庄铮.三相串联励磁式无轴承开关磁阻发电机原理与实现[J].电工技术学报,2013,28(2):108.CAO Xin,DENG Zhiquan,ZHUANG Zheng.Principle and implementation of a bearingless switched reluctance generator with three adjacent excitation-windings connected in series[J].Transactions of China Electrotechnical Society,2013,28(2):108.
[8] SUN Xiaodong,CHEN Long,YANG Zebing.Overview of bearingless permanent-magnet synchronous motors [J].IEEE Trans.on Industrial Electronics,2013,60(12):5529.
[9] BAI Haoran,WANG Fengxiang,XING Junqiang.Control strategy of combined pwm rectifier/inverter for a high speed generator power system[C]// Proceedings of IEEE Industrial Electronics and Applications,2007:132-135.
[10] AZZIDDIN M,RAZALI M A,RAHMAN.Performance analysis of three-phase PWM rectifier using direct power control[C]// Proceedings of IEEE International Electric Machines & Drives Conference,2011:1603-1608.
[11] LI Shuhui,HASKEW T A,SWATLOSKI R P,GATHINGS W.Optimal and direct-current vector control of direct-driven PMSG wind turbines[C]// Proceedings of IEEE Power Electronics Society, 2012,27(5):2325-2337.
[12] CAO Xin,DENG Zhiquan.A full-period generating mode for bearingless switched reluctance generators[J].IEEE Transactions Applied Superconductivity,2010,20(3):1072.
[13] 侯勇,童建东.变速恒频双馈风力发电机并网积分型变结构控制[J].电机与控制学报,2008,12(3):260.HOU Yong,TONG Jiandong.Cutting-in control of variable-speed constant-frequency double-fed wind-power generator with integral variable structure control[J].Electric Machines and Control,2008,12(3):260.
[14] HAO Chen,DAVID N,ALIPRANTIS D C.Analysis of permanent-magnet synchronous generator with vienna rectifier for wind energy conversion system[J].IEEE Transactions Sustainable Energy,2012:154.
(编辑:张 楠)
Bearinglesspermanentmagnetsynchronousgeneratorlevitationforceandelectricitygenerationperformanceundervariablespeedandloadsituation
DIAO Xiao-yan,HU Ya-min,ZHU Huang-qiu,LU Rong-hua,HUANG Jian-bo
(School of Electrical and Information Engineering,Jiangsu University,Zhenjiang 212013,China)
In terms of the serious abrasion of the normal generator bearing,the bearingless permanent magnet synchronous generator (BPMSG) was proposed.Suspension principle and the electric-generation principle of the bearingless permanent magnet synchronous generator were described.Secondly,the formula of the magnetic field energy storage was deduced.Then the mathematical model of the levitation force and electromagnetic torque were established on the basis of the Maxwell Tensor methods.Thirdly,structure of the machine was designed and optimized using parametric analysis mothed,and the correctness of the mathematical model was verified by simulation.Finally,aiming at the common problems of the ordinary permanent magnet synchronous generator under the variable speed and variable load conditions,the suspension forces and the electronic-generation performance were analyzed based on the finite element analysis (FEA).Simulation results show the BPMSM has good feasibility and suspension under the variable speed and variable load conditions.The research results show that the proposed BPMSG can operate steadily and has good static and dynamic performance.
bearingless permanent magnet synchronous generator; mathematical model; variable load,variable speed; performance analysis
10.15938/j.emc.2017.09.009
TM 351
:A
:1007-449X(2017)09-0063-10
2015-11-04
国家自然科学基金(51675244);江苏省重点研发计划项目(BE2016150);江苏高校优势学科建设工程资助项目(2014)
刁小燕(1979—),女,博士研究生,研究方向为无轴承电机设计及控制;胡亚民(1992—),男,硕士,研究方向为无轴承永磁同步发电机设计及控制;朱熀秋(1964—),男,博士,教授,博士生导师,研究方向为无轴承电机、磁轴承支承高速电机传动系统、特种电机非线性智能控制等;陆荣华(1991—),男,硕士,研究方向为无轴承永磁同步电机驱动及控制;黄建波(1991—),男,硕士,研究方向为异步启动无轴承永磁同步电机设计及控制。
刁小燕

