基于Spark的人工蜂群改进算法

翟光明，李国和,，吴卫江,，洪云峰，周晓明，汪 静

(1.中国石油大学(北京) 地球物理与信息工程学院，北京 102249； 2.中国石油大学(北京) 油气数据挖掘北京市重点实验室，北京 102249；3.石大兆信数字身份管理与物联网技术研究院，北京 100029) (*通信作者电子邮箱guangminz@163.com)

基于Spark的人工蜂群改进算法

翟光明1,2*，李国和1,2,3，吴卫江1,2,3，洪云峰3，周晓明3，汪 静1,2

(1.中国石油大学(北京) 地球物理与信息工程学院，北京 102249； 2.中国石油大学(北京) 油气数据挖掘北京市重点实验室，北京 102249；3.石大兆信数字身份管理与物联网技术研究院，北京 100029) (*通信作者电子邮箱guangminz@163.com)

针对人工蜂群(ABC)算法求解组合优化问题时效率低的问题，提出了基于Spark云计算框架的并行ABC改进算法。首先，将蜂群划分为子蜂群并将蜂群构造为弹性分布式数据集，子蜂群使用广播机制交换优秀个体；然后，采用一系列转换算子，实现蜜蜂寻找解过程的并行化；最后，用万有引力质量计算代替轮盘赌概率计算，减少计算量。通过旅行商问题(TSP)求解说明了算法的可行性。实验结果表明：对比标准ABC算法，所提算法加速比最大达到3.24；对比未改进的并行ABC算法，该算法收敛速度提高约10%。所提算法在复杂问题求解方面优势更加明显。

人工蜂群算法；Spark；并行；万有引力算法；旅行商问题

0 引言

人工蜂群(Artificial Bee Colony, ABC)算法是由土耳其埃尔吉耶斯大学Karabaga[1]于2005年提出的基于蜜蜂采蜜行为的元启发式搜索算法，具有群智能算法的特点，和结构简单、收敛速度快、容易实现等优点[1-2]。该算法基于蜜蜂的群体智能和自组织模型理论，具有天然的并行性特征，但也存在易早熟、收敛速度慢等问题。

人工蜂群算法具有搜索并行性，在单处理器环境下，只能以串行方式实现并行搜索，这种方式不适应大数据时代大规模增长的数据集。云计算技术的兴起为人工蜂群算法的并行化实现提供了一个很好解决思路，其融合了并行计算和分布式计算等技术，在大规模异构数据存储和逻辑计算具有卓越的性能表现[3]。本文在已有研究的基础上，基于Spark框架提出并行人工蜂群改进算法，从而解决大规模运算中ABC算法存在的时间复杂度过高的问题。

1 Spark云计算框架

1.1 Spark生态系统

云计算作为一种新的并行数据处理技术，融合了网格计算、分布式计算和并行计算的特点[3-4]。2003年起，Google公司相继发表了3篇奠定大数据算法基础的论文：Google文件系统(Google File System， GFS)[5]、大型结构化数据表(BigTable)[6]及大数据分布式计算模型(MapReduce)[7]。Apache基金会根据上述论文设计推出了Hadoop分布式系统基础架构，从而将全球云计算的研究推向一个高潮。当前，全球每天产生的数据量达到2 EB[8]，需要处理的数据量和问题规模都爆发式增长，结合云计算技术来拓展算法的数据处理和吞吐能力成为研究热点。

Spark云计算框架是美国加州伯克利大学算法机器人(Algorithms Machine People， AMP)实验室开发的基于内存计算的大数据并行计算框架。Spark是MapReduce计算模型的替代方案，弥补了采用MapReduce实现迭代式算法或对实时性有较高要求的应用需求时存在的CUP与数据I/O之间异步瓶颈问题[9]。图1展示了Spark生态系统，整个系统分为3层，最核心的是Spark Runtime，它包含了Spark最核心的功能和分布式算子。底层的Cluster Manager和Data Manager分别负责集群的资源管理和数据管理。最上层为Spark提供了丰富的计算范式，涵盖支持结构化数据查询与分析的查询引擎Spark SQL、分布式机器学习库MLlib、并行图计算框架GraphX、流计算框架Spark Streaming四个模块。

图1 Spark生态系统

Spark技术的兴起为众多机器学习算法提供了改进思路：Alitouka[10]实现了基于Spark的密度聚类算法；王桂兰等[11]研究了Spark环境下的并行模糊C均值聚类算法，定义了在Spark上完整的矩阵操作；牛海玲等[12]基于Spark框架将Apriori算法进行并行化处理，并与传统Apriori算法和基于Hadoop的Apriori算法进行性能上的比较。本文研究基于Spark实现人工蜂群算法的方法，期望与传统的实现进行对比，大幅提升算法性能。

1.2 Spark关键技术介绍

Spark将分布式数据抽象为弹性分布式数据集(Resilient Distributed Dataset， RDD)，其是分布式数据集在本地的抽象，能够使用户以本地操作的方式操作分布式环境中的数据集合。RDD提供了一种高度受限的共享内存，并且只能基于在稳定物理存储中的数据集和其他已有的RDD上执行确定性操作来创建，这些确定性操作称之为转换算子，如count、reduceBykey、partitionBy、union等。除了转换算子，Spark还提供输入算子、缓存算子和行动算子，Hadoop中提供的Map和Reduce操作也被封装进Spark的算子中。可以说Spark在继承Hadoop优秀基因的同时还提供了更为丰富的接口和操作[11]。

RDD数据同步是支持Spark集群各节点并行工作的重要保证。RDD目前提供两个数据同步的方法：广播(Broadcast)和累加器(Accumulator)。广播依靠广播变量实现变量共享，可以有效解决物理上隔离的两个节点之间访问公共数据的存储问题，广播变量是read-only的，变量修改后不会反馈到其他节点；累加器是一个write-only变量，用于累加各个任务中的状态，该状态变量可以被维护累加器的所有节点共享。

2 基于Spark的人工蜂群算法

2.1 人工蜂群算法

自然界中蜜蜂在采蜜时根据太阳位置记录自己蜜源的方位、离蜂巢的距离等信息[1-2]。人工蜂群算法模拟蜜蜂采蜜的群体智能行为，把蜂群分为引领蜂、侦察蜂和跟随蜂[13]。引领蜂确定蜜源的位置并指导蜂群的采蜜行为，待工蜂可变为跟随蜂或侦察蜂，跟随蜂增强种群对优良蜜源的找寻能力，侦察蜂保持种群的多样性并最终转换成跟随蜂或引领蜂。算法主要操作有引领蜂搜索、侦查蜂搜索和跟随蜂选择[14]。

1)引领蜂搜索。

引领蜂随机搜索区域并记忆初始蜜源位置，按式(1)对蜜源进行邻域搜索：

Vi,j=xi,j+φi,j·(xi,j-xk,j)

(1)

其中：Vi,j表示新的食物源，其在先前食物源xi,j和邻近食物源xk,j比较计算的基础上得到，j∈{1,2,…,D}，k∈{1,2,…,N}，D代表食物源中的参数维数，N表示食物源的数量；φi,j是[-1,1]区间的随机数。引领蜂对更新后食物源采用贪婪选择策略进行选取。

2)侦察蜂搜索。

ABC算法中食物源的邻域搜索次数存在一个阈值limit，是算法中控制质量没有改善的某个食物源的更新次数的重要参数。当某个食物源更新次数超过limit，质量却没有得到改善，该食物源将被新的食物源替换，此时引领蜂变为侦察蜂并按式(2)进行随机搜索产生新的食物源：

Xi,j=lbj+θ·(ubj-lbj)

(2)

其中：i代表第i个食物源，θ为(0,1)内随机数，ubj、lbj分别是第j维参数决定的食物源质量的上限和下限。

3)跟随蜂选择。

按式(3)计算每个引领蜂的选择概率，跟随蜂以轮盘赌原则选择引领蜂并跟随：

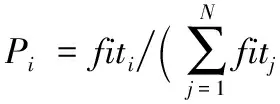
(3)

其中fiti代表第i个食物源的质量值，具体值由相应的适应度评价函数求得。蜜蜂被选中概率与自身适应度值成正比。跟随蜂选择食物源后同样按照式(1)搜索新食物源。

2.2 选择概率的改进

(4)

其中：mi表示蜜蜂的收益度比率；Mi表示蜜蜂的惯性质量，也就是选择概率；best表示最佳食物源；worst表示最差食物源；mi与蜜蜂本身的适应度值正相关，越优秀的个体越能保持迭代持续性，有效保证种群优良性。

2.3 人工蜂群优化算法的实现

人工蜂群算法具有天然的并行性，并行策略大致有：①并行独立蜂群，蜂群间无交互；②并行非独立子蜂群，子蜂群交互式并行搜索；③并行蜜蜂，即一个蜜蜂对应一个节点，各蜜蜂并行搜索。方式①忽略了蜜蜂之间的信息交流且需要大规模集群的支持。方式②、③本质上相同，考虑到蜂群算法中种群规模对算法的性能提升有一个阈值，种群过大反而会增加计算量，因此本文选取方式②作为Spark并行策略，提出基于Spark的人工蜂群改进算法——GABC-Spark(Gravitation Artificial Bee Colony based on Spark)。

图2展示了GABC-Spark算法的流程。每个子蜂群搜索解的过程并行，子蜂群内部搜索仍然串行，子蜂群对食物源的邻域搜索为一个独立的并行单元，因此，假设子蜂群规模为k，则N只蜜蜂组成的蜂群构成N/k个独立的并行单元。每次迭代完成个体按收益度值排序，记录子蜂群最优与最差食物源。之后，子蜂群广播自身最优食物源同时接收其他子蜂群的广播消息。当其他蜂群最优食物源更优秀时，子蜂群将自身最差食物源替换为获得的最优食物源，引领本身的下一次迭代。

图2 GABC-Spark算法流程

图3展示了算法在Spark实现并行的数据流图。通过数据流图描述算法并行化过程如下：将蜜蜂封装为类Bee，类中包含有Initialize()方法用于解的构造，LocalSearch()方法用于邻域搜索。生成蜂群就是初始化m个Bee类的实例，则蜂群规模NP的值为m。利用系统提供的ArrayList集合类封装m个Bee实例，之后使用SparkContext对象的parallelize()方法将对象数组创建为分布式RDD，记为RDD_a。调用RDD_a.map()算子将子蜂群映射到各子节点并调用Initialize()方法并行构造解，结果返回为格式为ArrayList[ArrayList[]]的RDD:RDD_b，然后再调用RDD_b.map()算子并行调用LoaclSearch()局部搜索方法，同样返回格式为ArrayList[ArrayList[]]的RDD:RDD_c。最后使用RDD的collect算子将分布式的RDD_c本地化，排序得到最优解。

需要注意的是，应用到实际问题时算法参数、当前最优个体等使用多次的数据需要缓存，否则会进行不必要的重复操作。RDD提供cache()方法来缓存共享数据。而问题求解的中间数据(如TSP中的转移概率和路径记录矩阵)使用broadcast广播机制发送广播信息，让蜂群所有蜜蜂可以互相交流通信。

图3 GABC-Spark算法数据流图

3 实验设计与结果分析

3.1 实验环境及算法参数

实验集群环境为阿里云ECS云服务器实例，安装64位Ubuntu 14.04系统，集群实验环境节点属性详见表1。单机环境属性为：Intel Xeon CPU，3.00 GHz四核；8 GB内存；500 GB机械硬盘；Windows 7 64 bit操作系统，Matlab R2012b。为保证实验的准确性，实验中算法参数均与文献[16]一致。

表1 集群属性

3.2 实验方案

以旅行商问题(Traveling Salesman Problem， TSP)为例，选用标准数据集开展实验。为了对比改进前后算法的加速效果，选用文献[17]中使用的eil51、ch130、tsp225作为实验数据。对人工蜂群算法按照文献[16]所述进行改造编码，该文献中人工蜂群算法与TSP对应关系如表2所示。根据文献[16]所述并结合本文概率计算式(4)，得到实验中蜜蜂的收益度计算公式如式(5)：

(5)

其中：fi代表路径欧氏距离的倒数，min(f)、max(f)分别表示蜂群中最差解和最优解，fibee是当前第ibee只蜜蜂的收益。

为证明本文算法的有效性和可用性，同ABC[16]、蚁群优化(Ant Colony Optimization， ACO)算法、基于Spark的蚁群优化算法(Ant Colony Optimization algorithm based on Spark， ACO-Spark)[17]进行比较实验，实验结果如表3所示。对实验结果使用双尾t-test双样本等方差假设检验[18-19]，比较ABC算法和GABC-Spark算法的解，结果如表4所示。表5为算法在节点数量不同的集群中搜索到目标解的平均时间花费，目标值时间是指eil51收敛到450、ch130收敛到6 500、tsp225收敛到4 500所花时间。

表2 ABC算法中蜂群觅食行为与TSP对应关系

表3 实验结果

3.3 实验结果与分析

由表3可知，ABC算法和GABC-Spark算法在寻优能力上略好于ACO算法，其最优解均为测试集已知的最优解。通过表4可知在统计学意义上GABC-Spark算法和ABC算法具有相同的寻优能力，证明改造前后的算法在寻优能力上并没有损失。

表4 双尾t-test检验结果

表5给出了在不同集群环境下算法收敛到目标值的时间，并得出了相对于单机Matlab中运行所花时间的加速比，其中eil51、ch130、tsp225单机平均运行时间分别29.10 s、151.28 s和492.22 s。总体来看相对于单机运行的ABC算法，GABC-Spark算法的加速比最高可达3.24且有持续增长的趋势，且随着问题规模的增加，加速效果愈加明显。实验结果表明GABC-Spark算法运行时间较基于Spark的标准人工蜂群算法(Algorithm of Artificial Bee Colony based on Spark， ABC-Spark)均有减少，在节点数为1时表现得尤为明显，随着集群规模的增加，算法总体迭代次数减少，GABC较ABC的加速效果开始减弱，因此，问题规模越大、算法迭代次数越多，GABC加速效果越显著。对于eil51测试集，GABC-Spark算法的搜索效率反而不如单机下运行，这是因为该测试集解空间不太复杂在单机下就能很好解决。而在Spark中因其TaskScheduler任务调度采用集中式调度以保证每个节点都有Task在执行，有一定的任务分配时间，加上算法运行中节点之间的大量通信时延所以其整体运行时间要高于Matlab下运行时间，并且随着节点数的增加，任务调度和通信时延逐步增长，运行时间也持续增加。在集群节点数为1时，算法的运行时间普遍高于单机下运行时间，这Spark本身关系外还有高级语言运行速度低于函数型语言外的原因，因此求解时间出现逆增长。对于ch130测试集，算法加速比先增后减，说明集群规模增加对算法程序性能提升存在一个瓶颈，当增加节点带来的计算效率的提升低于通信和任务调度时间消耗时，算法加速能力开始退化。tsp225测试集因为解空间较为复杂，所以加速比一直随着节点数增加而增长。可以预见，随着问题解空间复杂度的增大和计算规模的增加，算法加速比将会随着节点数的增加而持续提升。

表5 不同实验环境运行时间及加速比

4 结语

本文对人工蜂群算法结合Spark分布式计算框架实现并行化进行研究。首先介绍了人工蜂群算法的思想、流程，并对人工蜂群算法的3种并行方式进行了探讨。依据子蜂群交互式并行搜索策略实现人工蜂群算法的Spark并行化，使其能够运行在云计算集群中。针对算法选择概率计算复杂的问题，引入万有引力质量计算，替换基本算法中的轮盘赌概率计算，减轻了计算压力，并可以同时获得种群中蜜蜂收益度值的排名，降低搜索时间提升算法收敛速度，为进一步研究算法不同参数的性能表现和提升算法在集群下的运算效率奠定基础。

References)

[1] KARABOGA D. An idea based on honey bee swarm for numerical optimization [R]. Kayseri: Erciyes University, 2005.

[2] KARABOGA D, BASTURK B. On the performance of Artificial Bee Colony (ABC) algorithm [J]. Applied Soft Computing, 2008, 8(1): 687-697.

[3] 李乔,郑啸.云计算研究现状综述[J].计算机科学,2011,38(4):32-37.(LI Q, ZHENG X. Research survey of cloud computing [J]. Computer Science, 2011, 38(4): 32-37.)

[4] 林闯,苏文博,孟坤,等.云计算安全:架构、机制与模型评价[J].计算机学报,2013,36(9):1765-1784.(LIN C, SU W B, MENG K, et al. Cloud computing security: architecture, mechanism and modeling [J]. Chinese Journal of Computers, 2013, 36(9): 1765-1784.)

[5] GHEMAWAT S, GOBIOFF H, LEUNG S. The Google file system [C]// SOSP 2003: Proceedings of the Nineteenth ACM Symposium on Operating Systems Principles. New York: ACM Press, 2003: 29-43.

[6] CHANG F, DEAM J, GHEMAWAT S, et al. Bigtable: a distributed storage system for structured data [J]. ACM Transactions on Computer Systems, 2008, 26(2): 205-218.

[7] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters [J]. Communications of the ACM, 2008, 51(1): 107-117.

[8] 李建中,王宏志,高宏.大数据可用性的研究进展[J].软件学报,2016,27(7):1605-1625.(LI J Z, WANG H Z, GAO H. State-of-the-art of research on big data usability [J]. Journal of Software, 2016, 27(7): 1605-1625.)

[9] 宋杰,刘雪冰,朱志良,等.一种能效优化的MapReduce资源比模型[J].计算机学报,2015,38(1):59-73.(SONG J, LIU X B, ZHU Z L, et al. An energy-efficiency optimized resource ratio model for MapReduce [J]. Chinese Journal of Computers, 2015, 38(1): 59-73.)

[10] Alitouka. Spark-DBSCAN [EB/OL]. [2016- 10- 23]. https://github.com/alitouka/spark_dbscan.

[11] 王桂兰,周国亮,萨初日拉,等.Spark环境下的并行模糊C均值聚类算法[J].计算机应用,2016,36(2):342-347.(WANG G L, ZHOU G L, SA C, et al. Parallel fuzzy C-means clustering algorithm in Spark [J]. Journal of Computer Applications, 2016, 36(2): 342-347.)

[12] 牛海玲,鲁慧民,刘振杰.基于Spark的Apriori算法的改进[J].东北师大学报(自然科学版),2016,48(1):84-89.(NIU H L, LU H M, LIU Z J. The improvement and research of Apriori algorithm based on Spark [J]. Journal of Northeast Normal University (Natural Science Edition), 2016, 48(1): 84-89.)

[13] SABET S, FAROKHI F, SHOKOUHIFAR M. A novel artificial bee colony algorithm for the knapsack problem [C]// INISTA 2012: Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications. Piscataway, NJ: IEEE, 2012: 141-151.

[14] 杨进,马良.蜂群优化算法在车辆路径问题中的应用[J].计算机工程与应用,2010,46(5):214-216.(YANG J, MA L. Wasp colony algorithm for vehicle routing problem [J]. Computer Engineering and Applications, 2010, 46(5): 214-216.)

[15] 张维平,任雪飞,李国强,等.改进的万有引力搜索算法在函数优化中的应用[J].计算机应用,2013,35(5):1317-1320.(ZHANG W P, REN X F, LI G Q, et al. Improved gravitation search algorithm and its application to function optimization [J]. Journal of Computer Applications, 2013, 35(5): 1317-1320.)

[16] 胡中华,赵敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报,2009,29(11):978-982.(HU Z H, ZHAO M. Simulation on Traveling Salesman Problem (TSP) based on artificial bees colony algorithm [J]. Transaction of Beijing Institute of Technology, 2009, 29(11): 978-982.)

[17] 王诏远,王宏杰,邢焕来,等.基于Spark的蚁群优化算法[J].计算机应用,2015,35(10):2777-2780.(WANG Z Y, WANG H J, XING H L, et al. Ant colony optimization algorithm based on Spark [J]. Journal of Computer Applications, 2015, 35(10): 2777-2780.)

[18] CUI W, LI X, ZHOU S, et al. Investigation on process parameters of electrospinning system through orthogonal experimental design [J]. Journal of Applied Polymer Science, 2007, 103(5): 3105-3112.

[19] XING H, QU R, KENDALL G, et al. A path-oriented encoding evolutionary algorithm for network coding resource minimization [J] Journal of the Operational Research Society, 2013, 65(8): 1261-1277.

This work is partially supported by the National High Technology Research and Development Program (863 Program) of China (2009AA062802), the National Natural Science Foundation of China (60473125), Youth Innovation Fund of China National Petroleum Corporation (CNPC) (05E7013), Sub-project of the National Science and Technology Major Project (G5800- 08-ZS-WX), China University of Petroleum-Beijing Karamay Campus Research Start Fund (RCYJ2016B- 03- 001).

ZHAIGuangming, born in 1993, M. S. candidate. His research interests include data mining, knowledge discovery.

LIGuohe, born in 1965, Ph. D., professor. His research interests include artificial intelligence, machine learning, knowledge discovery.

WUWeijiang, born in 1971, Ph. D. candidate, associate professor. His research interests include artificial intelligence, knowledge discovery.

HONGYunfeng, born in 1966, engineer. His research interests include ERP, data management.

ZHOUXiaoming, born in 1963, M. S., engineer. His research interests include information management system, decision support.

WANGJing, born in 1989, M. S. candidate. Her research interests include data mining, knowledge discovery.

ImprovedalgorithmofartificialbeecolonybasedonSpark

ZHAI Guangming1,2*, LI Guohe1,2,3, WU Weijiang1,2,3, HONG Yunfeng3, ZHOU Xiaoming3, WANG Jing1,2

(1.CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum-Beijing,Beijing102249,China;2.BeijingKeyLabofDataMiningforPetroleumData,ChinaUniversityofPetroleum-Beijing,Beijing102249,China;3.PanPassInstituteofDigitalIdentificationManagementandInternetofThings,Beijing100029,China)

To combat low efficiency of Artificial Bee Colony (ABC) algorithm on solving combinatorial problem, a parallel ABC optimization algorithm based on Spark was presented. Firstly, the bee colony was divided into subgroups among which broadcast was used to transmit data, and then was constructed as a resilient distributed dataset. Secondly, a series of transformation operators were used to achieve the parallelization of the solution search. Finally, gravitational mass calculation was used to replace the roulette probability selection and reduce the time complexity. The simulation results in solving the Traveling Salesman Problem (TSP) prove the feasibility of the proposed parallel algorithm. The experimental results show that the proposed algorithm provides a 3.24x speedup over the standard ABC algorithm and its convergence speed is increased by about 10% compared with the unimproved parallel ABC algorithm. It has significant advantages in solving high dimensional problems.

Artificial Bee Colony (ABC) algorithm; Spark; paralleling; gravitational search algorithm; Traveling Salesman Problem (TSP)

TP301.6; TP18

:A

2017- 01- 24;

:2017- 02- 12。

国家863计划项目(2009AA062802)；国家自然科学基金资助项目(60473125)；中国石油(CNPC)石油科技中青年创新基金资助项目(05E7013)；国家重大科技专项子课题(G5800- 08-ZS-WX)；中国石油大学(北京)克拉玛依校区科研启动基金资助(RCYJ2016B- 03- 001)。

翟光明(1993—)，男，湖南怀化人，硕士研究生，主要研究方向：数据挖掘、知识发现； 李国和(1965—)，男，北京人，教授，博士，主要研究方向：人工智能、机器学习、知识发现； 吴卫江(1971—)，男，北京人，副教授，博士研究生，主要研究方向：人工智能、知识发现；洪云峰(1966—)，男，湖北武汉人，工程师，主要研究方向：ERP、数据管理； 周晓明(1963—)，男，湖北武汉人，工程师，硕士，主要研究方向：信息管理系统、决策支持； 汪静(1989—)，女，山东聊城人，硕士研究生，主要研究方向：数据挖掘、知识发现。

1001- 9081(2017)07- 1906- 05

10.11772/j.issn.1001- 9081.2017.07.1906