基于北斗和GPS的高分二号全色影像正射精度验证与分析

江威， 何国金， 龙腾飞， 尹然宇,3， 宋小璐，2， 袁益琴，2， 凌赛广，2

(1.中国科学院遥感与数字地球研究所,北京 100094； 2.中国科学院大学,北京 100049；3.中国地质大学(武汉)李四光学院,武汉 430074)

基于北斗和GPS的高分二号全色影像正射精度验证与分析

江威1,2， 何国金1， 龙腾飞1,2， 尹然宇1,3， 宋小璐1，2， 袁益琴1，2， 凌赛广1，2

(1.中国科学院遥感与数字地球研究所,北京 100094； 2.中国科学院大学,北京 100049；3.中国地质大学(武汉)李四光学院,武汉 430074)

高分二号(GF-2)卫星几何精纠正是其广泛应用的前提。以福州市作为实验区，选择北斗卫星导航系统(北斗)和GPS野外测量获取控制点和检查点，采用像方平移、像方漂移和像方仿射变换3种方法对有理函数模型进行误差补偿，验证分析控制点测量精度、分布、数目以及纠正方法对GF-2全色影像纠正的影响，并分析了北斗应用于GF-2全色影像正射纠正的潜力。实验结果表明： 少量分布均匀的控制点就可以消除GF-2全色影像纠正后的系统几何误差； 3种纠正方法中像方仿射变换方法精度最高，其中GPS控制测量下检查点平面均方根误差为1.49 m，北斗RTK控制测量下检查点平面均方根误差为1.51 m，GPS与北斗RTK控制测量下的影像纠正精度接近； 北斗2种测量模式中，只有RTK模式能够满足GF-2全色影像纠正需求。上述研究表明，GF-2全色影像能够利用GPS和北斗RTK模式控制测量下的少量分布均匀高精度控制点达到较高纠正精度，满足实际应用需求。

高分二号卫星； 北斗卫星导航系统； GPS； 几何纠正； 精度验证； 有理函数模型

0 引言

高分二号(GF-2)卫星是我国高分辨率对地观测系统中重大专项中首颗“亚米级”光学卫星，有效提升了我国对地观测能力[1]。高分辨率遥感图像正射纠正精度是评价遥感图像几何质量的重要指标之一[2]。以往研究中多采用1∶1万地形图和土地利用现状图等作为辅助图件进行影像纠正，由于我国经济快速发展带来土地覆盖急剧变化，这些辅助图件的现势性大多难以满足实际要求[3]，采用星载差分GPS获取高精度地物坐标作为控制点，已成为高分遥感影像几何精纠正常用办法。陈华等[3]利用星载差分GPS实测控制点对SPOT5卫星影像的几何纠正模型进行实验，得出正射模型法纠正精度高于多项式纠正精度。代华兵[4]利用差分GPS对SPOT5影像林区进行了正射纠正，控制点中误差为1.337个像元，能够满足应用需求。针对国产资源三号(ZY-3)卫星，唐新明[5]等利用GPS测量点验证ZY-3有理函数模型(rational function model，RFM)几何纠正精度，在四角布设控制点情况下，DOM平面精度高于3 m，DSM高程精度高于2 m。刘斌[6]等采用差分GPS在平地和山地典型区域测量，进一步验证ZY-3卫星影像精度，认为其精度能满足1∶5万DEM及DOM制作要求。刘荣杰[7]等采用高精度GPS测量验证我国海岸带区域ZY-3卫星定位精度，表明ZY- 3影像在少量控制点下也能达到较高的纠正精度。

2012年我国自主研发的北斗卫星导航系统(下文简称北斗)开始运行，目前已成为继GPS，GLONASS和Galileo的全球第四大卫星导航系统[8]。杨元喜[9]等评估了北斗区域卫星导航系统建成运行后的基本导航定位性能，发现北斗单频伪距单点定位精度高于6 m，高程精度高于10 m，三维点位精度高于12 m，而载波相位差分定位精度与GPS处于同一水平，超短基线情况下，三维定位精度高于1 cm，短基线情况下高于3 cm。郁聪冲[10]等对北斗卫星精度衰减因子和卫星数进行了分析，无论是高纬度地区还是低纬度地区，在最小仰角15°的条件下，都能全天候满足测量要求。王仲锋[11-12]等研究北斗卫星导航系统实时差分(real-time kinematic，RTK)定位和静态定位精度，得出RTK测量和GPS的平面定位精度基本在同一量级，静态组网测量平差平面精度也与GPS在同一个量级上的结论。

从以上文献可知，目前主要利用GPS验证分析国外高分卫星以及国产资源卫星和高分一号影像正射纠正精度，但针对GF-2全色影像正射纠正精度验证分析未有报道； 另外，我国北斗目前已经建成运行，目前也未有将北斗测量控制点应用于GF-2卫星正射纠正的研究。因此，本文通过差分GPS和北斗野外测量，验证分析控制点测量精度、分布、数目以及纠正方法对影像正射纠正精度的影响，并分析北斗应用于GF-2全色影像正射纠正的潜力，以期为GF-2卫星影像高精度定位提供参考。

1 数据介绍

实验选取了福州市地区GF-2卫星遥感影像，传感器参数如表1。该数据为1A级，经过了数据解析、均一化辐射校正、去噪、MTFC、CCD拼接及波段配准等处理[2]。数据成像时间为2014年11月4日，采用影像的全色波段进行几何纠正精度验证。

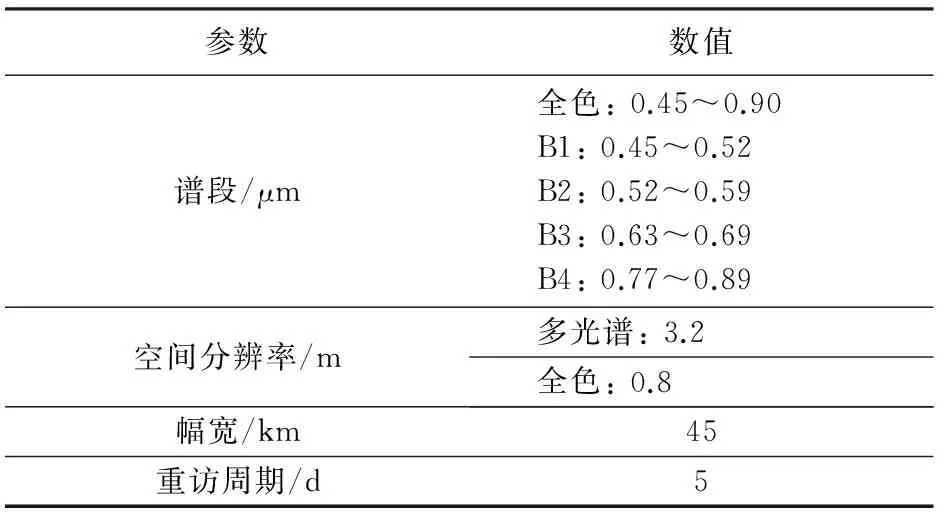
表1 GF-2卫星传感器主要参数

外业测量仪器分为北斗和GPS。北斗仪器型号为中绘i60 GNSS，该仪器可采用 RTK和静态2种测量模式，其中RTK模式为与已知点基站进行实时差分，静态模式是利用卫星和接收机直接确定坐标位置； GPS为NAVCOM公司的SF-3040型仪器，该仪器是通过与卫星进行实时差分获得高精度坐标位置。在实际测量中，GPS水平测量精度高于0.4 m，垂直精度高于0.5 m； 北斗RTK模式水平测量精度高于0.1 m，垂直精度高于0.1 m，北斗静态模式水平测量精度高于3 m，垂直精度高于4 m。GPS和北斗RTK模式测量水平和垂直精度均高于正射影像的空间分辨率。虽然北斗静态模式测量精度较低，基于全面分析北斗用于GF-2影像正射纠正潜力的考虑，也一并对其进行了分析。为客观对比测量精度，每个点均采用2套仪器测量，共采集36个点，北斗测量的RTK模式27个点，静态模式为9个点。用于正射的全色影像和测量点位置分布如图1。

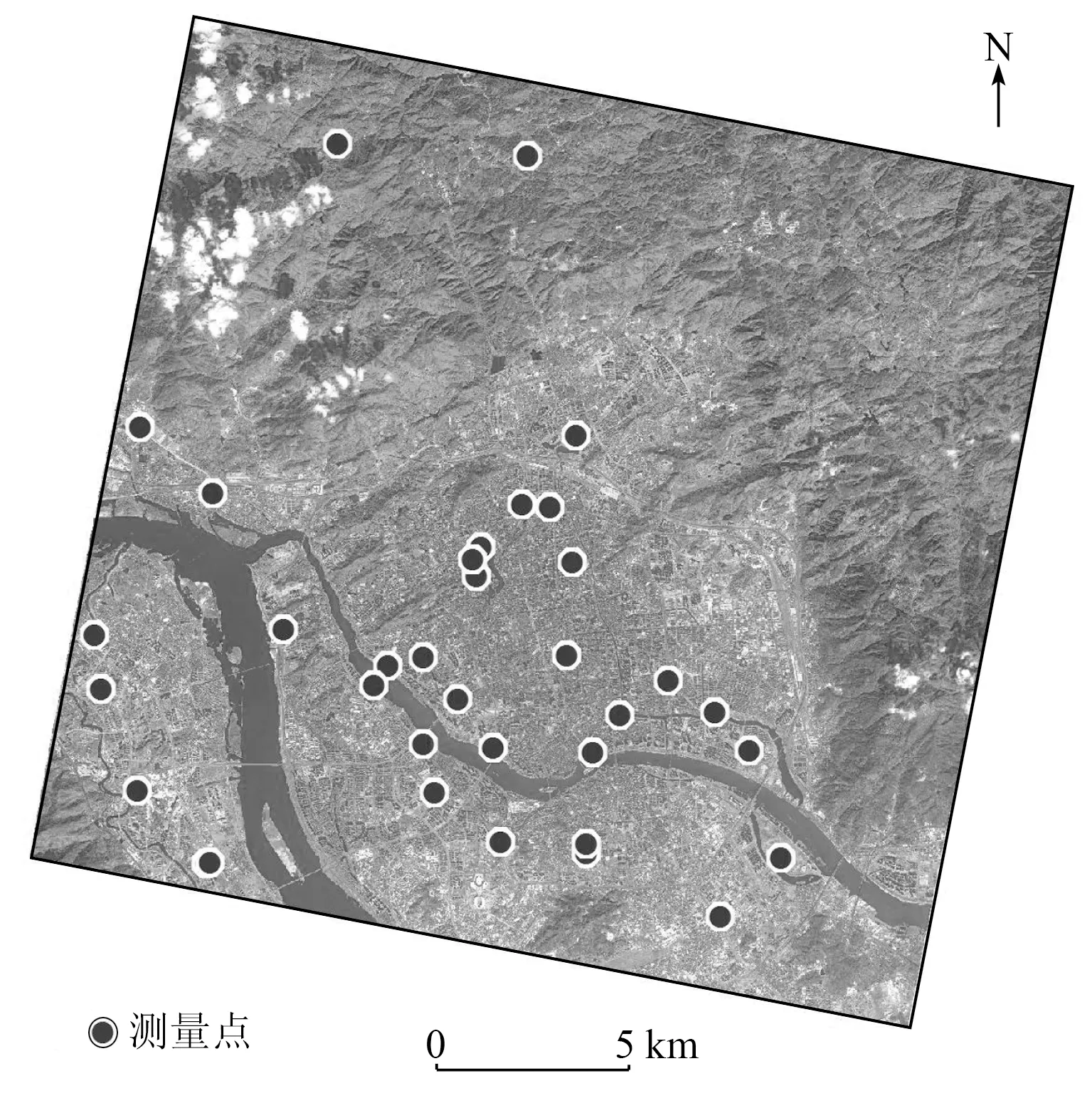
图1 GF-2全色影像和测量点分布

2 正射纠正方法与精度评价

GF-2影像带有理函数多项式系数(rational polynomial coefficients，RPCs)，可以采用RFM模型进行无控制点几何纠正。RFM模型形式简单，能够将地面点空间坐标(X,Y,Z)与对应的像素坐标(r,c)由比值多项式关联起来[13-14]，定义为[15]

(1)

式中，(rn,cn)和(Xn,Yn,Zn)分别为像素坐标(r,c)和地面坐标(X,Y,Z)经过平移和缩放后正则化坐标，当P1(Xn,Yn,Zn)多项式最高不超过3次时，该方程形式可以转换为

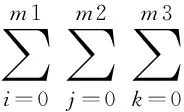
a10ZYX+a11Z2Y+a12Z2X+a13Y2Z+a14Y2X+a15Z2X+a16YX2+a17Z3+a18Y3+a19X3,

(2)

式中，ai(i=0,1…19)为RPC。

但由于星载传感器的成像外方位元素(主要是角元素)测量精度不足，直接使用影像自带RPC进行无控制点纠正的几何精度较低，在实际应用中通常需要借助地面控制点对初始RFM的误差进行补偿，以提高纠正精度。常用的补偿方式为像方多项式改正，如式(3)所示。具体有像方平移改正(含a0和b0)、像方漂移改正(含a0，a1，b0和b1)、像方仿射变换改正(含a0，a1，a2，b0，b1和b2)等[13]，即

(3)

式中：r和c为由自带RPC计算得到的行、列坐标值；R和C为经过像方补偿后的行、列坐标值；a0～b2为像方多项式改正系数。精度评价采用均方根误差和最大误差指标进行评价[3]，其中均方根误差公式为

(4)

式中：RMS表示均方根误差；n为样本数； △Xi和△Yi分别为第i个点X和Y方向误差，计算公式为

(5)

式中：Xi，计算和Yi，计算分别为第i个点由正射纠正模型计算得到图像X和Y方向坐标；Xi，测量和Xi，测量分别为第i个点由测量控制点所对应的图像X和Y方向坐标。

3 实验验证与结果分析

3.1 基于GPS控制测量的GF-2全色影像几何纠 正精度分析

采用GPS测量的18个控制点修正自带RPC的偏差，并进行几何纠正。分别采用像方平移改正、像方漂移改正和像方仿射变换改正3种方法进行改正； 然后将剩余的18个测量点作为检查点验证纠正精度，结果如表2。由表中可知，尽管部分检查点的误差大于2 m，3种方法改正后的检查点平面均方根误差均小于2 m，其中仿射变换改正方法的纠正精度最高，检查点平面均方根误差为1.39 m。这表明GF-2影像的内部精度较高，采用变换改正能消除大部分初始偏差，在3种纠正方法中，仿射变换改正方法最好。

表2 GPS GF-2全色影像纠正精度

图2是无控制点纠正影像位置偏移矢量，可以说明影像自带的RPC纠正内部误差具有系统性。图3为采用GPS控制测量点下仿射变换改正影像纠正位移偏移矢量，可看出控制点和检查点的误差分布无明显规律，表明影像的系统几何误差已消除，误差精度也有大幅度提高。

图2 无控制点影像几何纠正位置偏移矢量

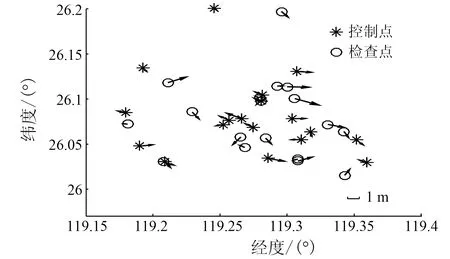
图3 GPS控制测量下仿射变换改正影像几何纠正位置偏移矢量

进一步验证GPS测量下控制点数量和分布对GF-2全色影像几何纠正的影响，选取测量点中靠近影像边缘的4个点作为控制点，其余测量点作为检查点进行精度验证，纠正结果见表3。3种纠正方法中，仿射变化改正方法纠正精度最高，检查点均方根误差为1.49 m。与表2相比，3种方法检查点平面均方根误差与18个控制点下纠正精度接近。

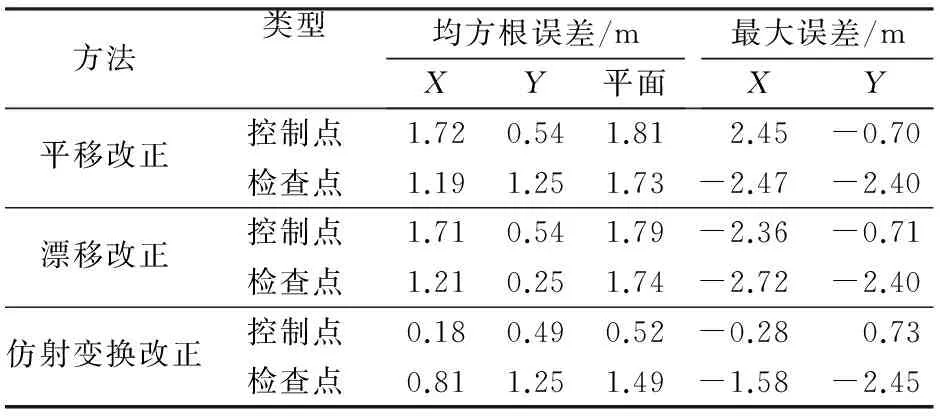
表3 少量GPS控制点下GF-2全色影像纠正精度

少量GPS控制点仿射变化改正影像几何纠正位置偏移矢量见图4。综合分析图2、图3和图4，说明GF-2全色影像纠正误差主要是系统误差，且误差具有一定的规律性，采用少量控制点也能够消除系统几何误差，提高几何纠正精度。通过表2和表3结果对比可以看出，在4个控制点和18个控制点条件下，采取少量分布均匀的高精度控制点即可获得较高的正射纠正精度。

图4 少量GPS控制点下仿射变换改正影像几何纠正位置偏移矢量

3.2 基于北斗控制测量下GF-2全色影像几何纠正精度

在36个控制点中，北斗RTK测量点27个，静态测量点9个，虽然北斗测量时给出了收敛精度，但由于目前关于北斗测量精度还未有广泛得到应用探讨，而GPS的测量精度已经在多年的实际工程中得到验证，为更客观说明本文北斗所采集的控制点精度，本文将北斗2种模式测量点与同一位置GPS测量点进行了精度对比，结果见表4。

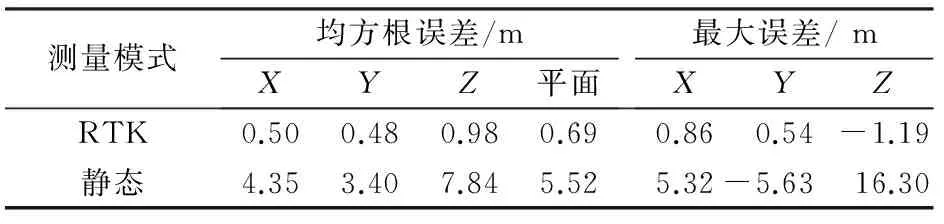
表4 RTK与静态测量精度对比

结果表明北斗RTK测量各精度评价指标均高于静态测量，RTK测量的X，Y和Z这3个方向均方根误差分别为0.50 m，0.48 m和0.98 m，平面均方根误差为0.69 m，静态测量的平面均方根误差为5.52 m，且各方向最大误差静态测量也显著大于RTK。本文的测量精度与杨元喜[9]评估的北斗定位精度一致，与王仲锋[11-12]实测北斗RTK精度也一致。综合表明北斗RTK测量精度能够符合GF-2全色影像纠正所需控制点精度要求。

根据3.1中可采取少量控制点对GF-2进行正射纠正和北斗的RTK模式测量精度符合GF-2影像纠正要求的结论，选取4个北斗RTK模式测量点作为控制点，剩余的23个测量点作为检查点，采用不同纠正方法验证了北斗RTK控制测量下的GF-2全色影像正射精度。纠正结果见表5。

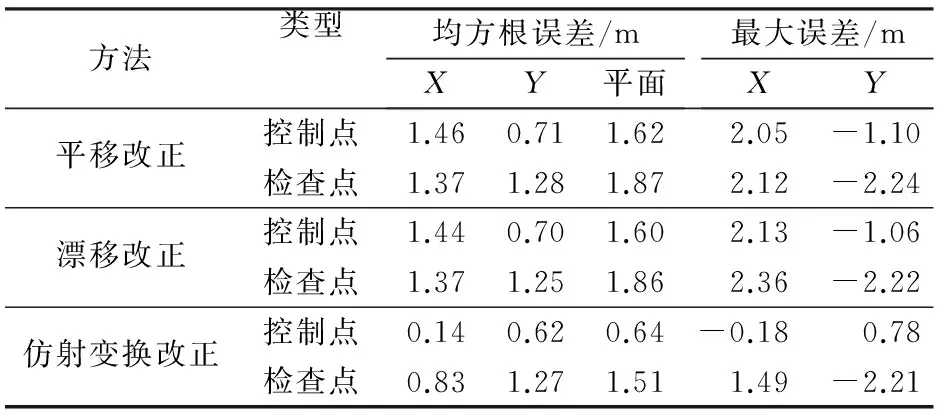
表5 北斗RTK模式GF-2全色影像纠正精度

由表5可知，部分检查点最大误差大于2 m，但3种方法改正后检查点均方根误差与GPS控制点测量下正射纠正结果接近，仿射变换改正的精度也是最高，检查点平面均方根误差为1.51 m，可满足GF-2全色影像的几何纠正精度需求。图5是北斗RTK测量控制下用于GF-2全色影像几何纠正位置偏移矢量图，从该图可以看出，误差的方向性规律不明显，系统几何误差已经消除。

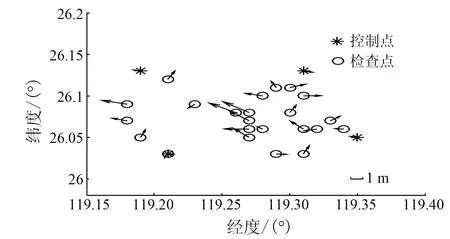
图5 北斗RTK控制测量下的仿射变换改正影像几何纠正位置偏移矢量

4 结论

本文采用北斗导航定位系统和GPS外业实测点，验证分析了控制点测量精度、分布、数目以及纠正方法对GF-2全色影像正射精度的影响，并进一步验证了北斗应用于GF-2号影像潜力，得出以下结论：

1) 无控制点GF-2全色影像RPC纠正后以系统误差为主。在实际应用中，可以采取少量分布均匀的高精度控制点对影像进行高精度的正射纠正。

2) 在选取的3种纠正方法中，仿射变换改正的方法精度最高，少量GPS控制测量下检查点平面均方根误差为1.49 m，少量北斗RTK控制测量点下检查点平面均方根误差为1.51 m，GPS与北斗RTK测量下GF-2全色影像正射纠正精度接近，两种方法均能满足应用需求。

3) 北斗2种测量模式中，只有RTK测量模式能够满足GF-2全色影像纠正所需控制点精度要求。

在实际外业测量过程中，北斗RTK通过与建立地面已知点基站进行实时差分获得高精度位置信息，相比于GPS与卫星实时差分测量，优势为单点测量时间短，约为30 s，高精度差分GPS收敛时长约为3 min； 劣势是基站架设时间长，覆盖范围有限，城市区域约为8～10 km，与基站通讯信号受高大建筑物遮挡明显。此外，北斗卫星信号受高大建筑物遮挡影响显著，尤其是南面高大建筑物，这可能与北斗目前在轨卫星数量较少有关。

[1] 潘腾,关晖,贺玮.“高分二号”卫星遥感技术[J].航天返回与遥感,2015,36(4):16-24. Pan T,Guan H,He W.GF-2 satellite remote sensing technology[J].Spacecraft Recovery & Remote Sensing,2015,36(4):16-24.

[2] 黄世存,吴海平,冯登超.高分一号多光谱高分相机全色图像正射精度验证与分析[J].遥感信息,2015,30(2):85-88. Huang S C,Wu H P,Feng D C.Ortho accuracy analysis of GF-1 PAN imagery[J].Remote Sensing Information,2015,30(2):85-88.

[3] 陈华,安娜,杨清华.基于GPS实测控制点的SPOT5 1A数据几何校正方法精度比较[J].国土资源遥感,2007,19(4):47-50,doi:10.6046/gtzyyg.2007.04.10. Chen H,An N,Yang Q H.Geometric correction methods of SPOT5 1A data based on GPS-measured ground control points[J].Remote Sensing for Land and Resources,2007,19(4):47-50,doi:10.6046/gtzyyg.2007.04.10.

[4] 代华兵,李春干,李政国.基于星站差分GPS及DEM的林区SPOT5数据正射校正[J].林业资源管理,2006(3):68-71. Dai H B,Li C G,Li Z G.Orthorectification of SPOT5 data of forest area based on WADGPS and DEM[J].Forest Resources Management,2006(3):68-71.

[5] 唐新明,张过,祝小勇,等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J].测绘学报,2012,41(2):191-198. Tang X M,Zhang G,Zhu X Y,et al.Triple linear-array imaging geometry model of Ziyuan-3 surveying satellite and its validation[J].Acta Geodaetica et Cartographica Sinica,2012,41(2):191-198.

[6] 刘斌,孙喜亮,邸凯昌,等.资源三号卫星传感器校正产品定位精度验证与分析[J].国土资源遥感,2012,24(4):36-40.doi:10.6046/gtzyyg.2012.04.07. Liu B,Sun X L,Di K C,et al.Accuracy analysis and validation of ZY-3's sensor corrected products[J].Remote Sensing for Land and Resources,2012,24(4):36-40.doi:10.6046/gtzyyg.2012.04.07.

[7] 刘荣杰,张杰,李晓敏,等.ZY-3影像在我国海岸带区域的定位精度评价[J].国土资源遥感,2014,26(3):141-145.doi:10.6046/gtzyyg.2014.03.23. Liu R J,Zhang J,Li X M,et al.Position precision evaluation of ZY-3 satellite image in the coastal zone of China[J].Remote Sensing for Land and Resources,2014,26(3):141-145.doi:10.6046/gtzyyg.2014.03.23.

[8] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6. Yang Y X.Progress,contribution and challenges of compass/Beidou satellite navigation system[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):1-6.

[9] 杨元喜,李金龙,王爱兵,等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学(地球科学),2014,44(1):72-81. Yang Y X,Li J L,Wang A B,et al.Preliminary assessment of the navigation and positioning performance of Beidou regional navigation satellite system[J].Science China Earth Sciences,2014,57(1):144-152.

[10]郁聪冲,边少锋.现阶段北斗卫星导航系统可用性分析[J].海洋测绘,2012,32(5):74-76. Yu C C,Bian S F.Usability analysis of beidou satellite navigation system at the present stage[J].Hydrographic Surveying and Charting,2012,32(5):74-76.

[11]王仲锋,林灿,历亮.北斗静态定位实验与精度分析[J].测绘与空间地理信息,2014,37(1):17-18. Wang Z F,Lin C,Li L.Static positioning test and precision analysis of compass[J].Geomatics & Spatial Information Technology,2014,37(1):17-18.

[12]王仲锋,禹东彬,唐铭蔚.北斗RTK的定位实验与精度分析[J].长春工程学院学报(自然科学版),2014,15(2):79-81. Wang Z F,Yu D B,Tang M W.Positioning test and precision analysis of compass RTK[J].Journal of Changchun Institute of Technology(Natural Science Edition),2014,15(2):79-81.

[13]Grodecki J,Dial G.Block adjustment of high-resolution satellite images described by rational polynomials[J].Photogrammetric Engineering & Remote Sensing,2003,69(1):59-68.

[14]Long T F,Jiao W L,He G J.Nested regression based optimal selection(NRBOS) of rational polynomial coefficients[J].Photogrammetric Engineering & Remote Sensing,2014,80(3):261-269.

[15]袁修孝,汪韬阳.CBERS-02B卫星遥感影像的区域网平差[J].遥感学报,2012,16(2):310-324. Yuan X X,Wang T Y.Block adjustment for CBERS-02B satellite images[J].Journal of Remote Sensing,2012,16(2):310-324.

(责任编辑：李瑜)

OrthoaccuracyvalidationandanalysisofGF-2PANimagerybasedonBeidousatellitenavigationsystemandGPS

JINAG Wei1,2, HE Guojin1, LONG Tengfei1,2, YIN Ranyu1,3, SONG Xiaolu1,2, YUAN Yiqin1,2, LING Saiguang1,2

(1.InstituteofRemoteSensingandDigitalEarth,ChineseAcademyofSciences,Beijing100094,China; 2.UniversityofChineseAcademyofSciences,Beijing100049,China; 3.CollegeofLisiguang,ChinaUniversityofGeosciences(Wuhan),Wuhan430074,China)

High geometric correction precision of GF-2 is a prerequisite for its widespread application. In this study, the authors selected Fuzhou as an experimental area. The ground control points (GCPs) were measured by Beidou satellite navigation system (BDS) and GPS respectively in the experimental area, which were used for geometric correction of the GF-2 panchromatic (PAN) image. The rational function model (RFM) was corrected by block adjustment with ground measurement point. The authors validated control point accuracy, distribution, as well as correction method for GF-2 panchromatic image correction, and analyzed the potential application to GF-2 PAN imagery geometric correction. The results show that a few control points can eliminate geometric error of GF-2 PAN imagery system. Affine transformation can reach the highest correction precision among three correction methods. Plane root mean square error (RMSE) of GPS check points using affine transformation is 1.49m and plane RMSE of Beidou RTK check points using affine transformation is 1.51m. In the two measuring modes of Beidou, Beidou RTK precision can satisfy the demand of GF-2 PAN imagery correction. The results show that, with a few high precision control points using GPS and Beidou RTK, GF-2 PAN imagery can reach high geometric correction accuracy and satisfy the demand of practical application.

GF-2 satellite image； Beidou satellite navigation system； GPS； ortho-rectification； accuracy validation； rational function model

10.6046/gtzyyg.2017.03.31

江威，何国金，龙腾飞,等.基于北斗和GPS的高分二号全色影像正射精度验证与分析[J].国土资源遥感，2017，29(3)：211-216.(Jiang W,He G J,Long T F,et al.Ortho accuracy validation and analysis of GF-2 PAN imagery based on Beidou satellite navigation system and GPS[J].Remote Sensing for Land and Resources,2017,29(3):211-216.)

2015-12-29；

2016-03-28

国家重点研发计划全球变化及应对专项项目“大尺度全球变化数据产品快速生成方法”(编号： 2016YFA0600302)、海南省重大科技计划项目“海南省遥感大数据服务平台建设与应用示范”(编号： ZDKJ2016021)和海南省重大科技计划项目“新型海洋信息感知关键技术及设备研发”(编号： ZDKJ2016015-1)共同资助。

江威(1991-)，男，博士研究生，主要从事遥感图像处理与夜间灯光遥感应用方面研究。Email: jiangweifz@163.com。

何国金(1968-)，男，研究员，博士生导师，主要从事遥感信息挖掘与智能处理。Email: hegj@radi.ac.cn。

TP 751.1

： A

： 1001-070X(2017)03-0211-06