基于模糊理论的山区高速公路长大隧道交通安全综合评价实证分析

张龙生，周小勇，张 兵，邹云霞

(1.江西交通咨询公司，江西 南昌 330008；2.江西省交通科学研究院，江西 南昌 330200；3.江西省交通规划勘察设计院，江西 南昌 330003)

基于模糊理论的山区高速公路长大隧道交通安全综合评价实证分析

张龙生1，周小勇1，张 兵2，邹云霞3

(1.江西交通咨询公司，江西 南昌 330008；2.江西省交通科学研究院，江西 南昌 330200；3.江西省交通规划勘察设计院，江西 南昌 330003)

针对交通运营特点进行分析，总结影响隧道交通安全的各项因素，建立山区高速公路长大隧道交通安全评价指标体系，运用层次分析法和模糊数学理论构建综合评价模型，最后以江西省九岭山隧道为例进行实证分析。

隧道；模糊理论；交通安全评价

1 山区高速公路长大隧道交通安全评价指标体系设计

山区高速公路长大隧道交通安全综合评价首先要构建具有科学性和全面性的评价指标体系，在指标的选取中，覆盖面要广，具有一定的评价可操作性，应着重筛选出表征性强、数据来源准确可靠并且容易获得的评价指标。确定综合评价指标也是整个评价体系的关键，是评价结论科学合理的有效保证。根据山区高速公路长大隧道交通安全评价的目的和原则，为了全方位地反映隧道内交通安全问题，所选指标要尽可能的客观反映影响行车安全的各方面因素。构建山区高速公路长大隧道交通安全综合评价指标体系如图1所示。

图1 山区高速公路长大隧道交通安全评价指标体系

2 山区高速公路长大隧道交通安全模糊评价模型

当前，综合评价模型的种类比较繁多，大体上分为两种类型，一种是直接给出评价结论数值，一种是通过评价指标的属性等级给出综合评定等级。山区高速公路长大隧道交通安全的评价具有一定的衡量对比标准，不能直接给出评价结论数值，需要根据评价指标的属性值综合判定最终结果的好坏，因此必须给出评定结果的所属评价等级。但是，在综合评价指标体系中，除了一些指标可以用定量数据准确地描述以外，还有很多指标难用定量数据确定，具有一定的模糊性，为了合理地确定指标属性值的评价等级，利用模糊数学理论中的模糊信息进行有效评价，可以很好地解决评价等级所属问题。

模糊数学的基本思想是确定指标值的隶属程度，即在综合评价过程中建立符合实际的各指标评价等级隶属函数。模糊评价首选需要对指标的隶属度进行评价，即指标的标准化处理。根据指标特性不同，模糊综合评价具有不同的隶属度函数，按照指标类型分类有成本型隶属度函数、效益型隶属度函数等，按照隶属函数的形式分类又分为三角形、矩形、梯形、指数和曲线型分布函数等。

根据已有文献研究结果，基于三角形隶属函数、曲线型函数的模糊综合评判模型可以实现评价结果隶属度向量的离散化，比利用梯形等隶属函数模型所求得的评价结果模糊度要小，根据隧道交通安全评价指标体系中的指标特性和评价过程科学简易原则，选取三角形隶属度函数，确定评价指标属性值评定等级。

山区高速公路长大隧道交通安全评价模型建立步骤为：

首先要确定综合评价集，由山区高速公路长大隧道交通安全评价指标体系可知，本模型采用二级模糊综合评判法，最上层的因素集组成为：

U={U1，U2，U3，U4}={隧道交通特性，驾驶员特性，交通设施，隧道运行环境，其他影响因素}

其次，建立各子评价集的子因素Uij，例如={U11，U12，U13，U14}{交通负荷度，行车速度，车头时距，大车比例}。

再次，通过对山区高速公路长大隧道行车安全的分析，确定各评价指标因素的权重值，本文利用层次分析法(专家打分)确定各指标的权值，得出综合权值矩阵W。

最后，确定最终评语集为{好，较好，一般，较差，差}五个等级，通过三角形隶属度函数给出隶属度值建立评价矩阵Ri。通过建立总评价矩阵以及综合权值矩阵W，得出模糊综合评价向量值S=W·R。根据五个等级的隶属度，确定最后评价结论所属等级。

3 实证分析

3.1 评价指标属性值及权值

(1)指标属性值

山区高速公路长大隧道交通安全评价指标属性值获取，主要采用实测方法或专家打分方法获得。对一些容易测量得到的指标属性值，例如交通流量(计算交通负荷度)、行车车速、车头时距、大车比例、噪声和路面湿度等指标，采用现场工具测的，而对主观评价指标属性值，则采用有经验的专家和司机打分的方式获取，运用隶属度函数来确定指标评语等级中的对应隶属度数值。

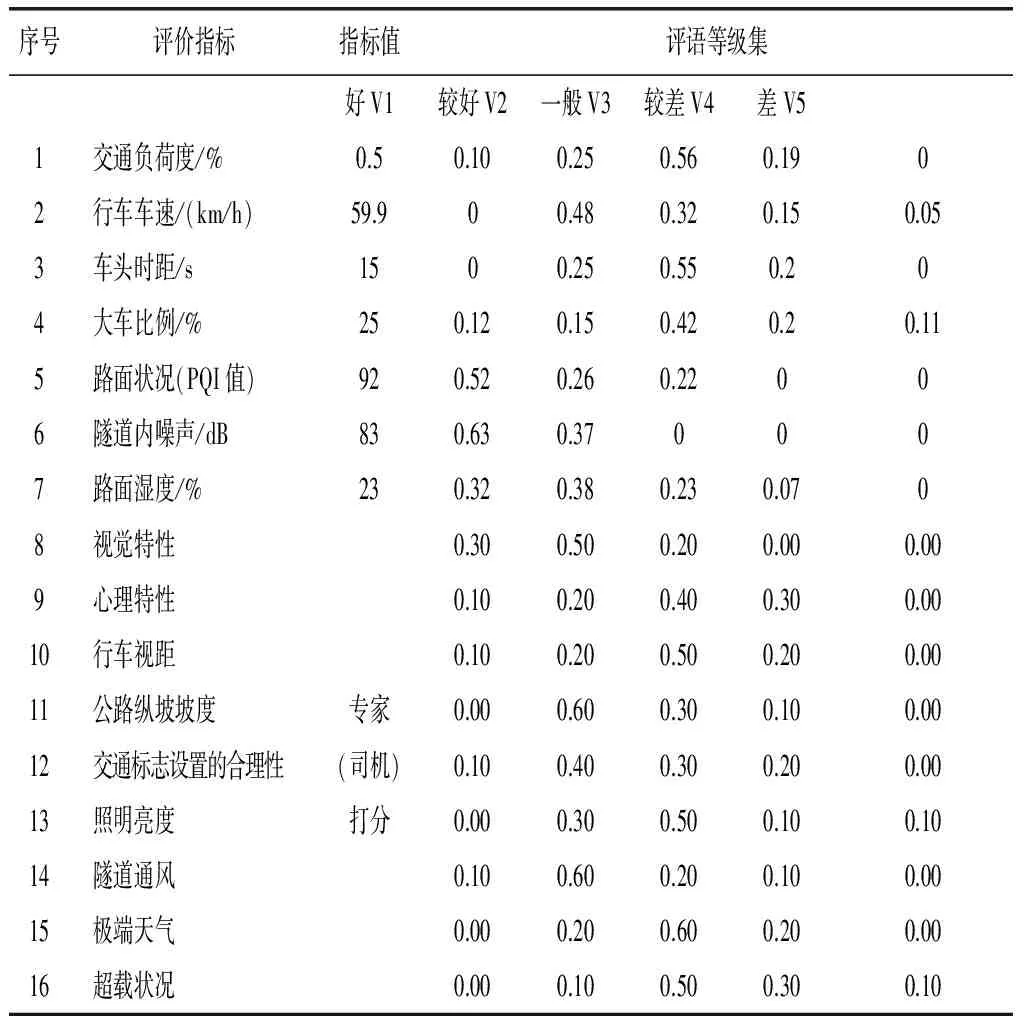
表1 九岭山隧道交通安全状况评价指标值及评语等级

(2)指标权值确定

为了确定评价指标的权值，采用专家问询表的形式对各个指标的相对重要性进行打分，构造判断矩阵，运用层次分析法计算各个指标的权值。在专家选择上，着重选择在交通工程、道路工程方面具有丰富经验而且长期在高速公路管理、道路交通安全研究等领域工作的10位专家进行问卷调查，因此具有较高的可信度。在问卷调查中，每位专家根据自身的工作背景独立填写问卷，对评价指标体系中的各个指标进行两两比较，确定每个指标的相对重要性，而且保证判断矩阵符合一致性检验，即CR<0.1。最后，赋予每位专家一样的权重，对指标进行进行加权算术平均，得到较为合理的权重值，如表2所示。

3.2 九岭山隧道行车安全的综合评价

(1)构建模糊评判矩阵

通过表1的数据，可以得到评判矩阵如下：其中R1、R1、R3、R4、R5分别为山区高速公路长大隧道交通特性(B1)、驾驶员特性(B2)、交通设施(B3)、隧道运行环境(B4)、其它因素(B5)的模糊评判矩阵。

表2 专家打分确定指标权重

(2)综合模糊评价

根据表2，可以得到隧道交通特性、驾驶员特性、交通设施、隧道环境、其它影响因素以及二级指标所对应的指标权值。

W1=[0.251，0.331，0.192，0.226]；W2=[0.374，0.485，0.141]；

W3=[0.193，0.605，0.202]；W4=[0.216，0.061，0.339，0.384]；

W5=[0.30，0.70]；

W=[0.312，0.157，0.221，0.228，0.082]。

利用matlab软件，对综合评价指标体系中的二级指标进行加权平均计算，并将计算结果组合形成一级指标的模糊综合评价矩阵R=[S1、S2、S3、S4、S5]。

S1=W1*R1；S2=W2*R2；S3=W3*R3；S4=W4*R4；S5=W5*R5；

最后，山区高速公路长大隧道模糊综合评价结果向量S=W*R。对九岭山隧道交通安全综合模糊评价实证分析得出各一级指标的模糊隶属度和综合评价值的模糊隶属度如表3所示。

表3 九岭山隧道交通安全综合评价结果

可以看出，根据综合评价结果的各个等级的隶属度可以看出，九岭山隧道交通安全评价等级中，隶属于“较好”等级的隶属度值最大，为0.366，其余依次为“一般”等级(隶属度为0.359)、“较差”等级(隶属度为0.147)、“好”(隶属度为0.113)，“差”等级(隶属度为0.050)。

4 结 语

(1)九岭山隧道的行车安全状态较好，在当前交通流量和交通安全设施下，隧道的交通安全能够得到保障，同时，由于隧道内通风设施、照明设施的设计合理性，驾驶员在隧道内行驶的舒适性较好，满意度也较高。

(2)九岭山隧道交通流构成中，大型车辆的占比较高，大型车辆尤其是超载货车的行驶速度、加减速度较慢，对正常交通流干扰比较明显，同时部分大型车辆在隧道内加速超车现象，增加了隧道内行车安全隐患，降低了评价等级。

(3)模糊理论应用于多因子、评价指标定性区间较大范围的综合评价有较好的实际效果。从综合评价结果分析上看，与从交通运行状况直观判定的结论基本相符，说明该综合评价模型具有一定的适用性。

[1] 赵倩，毛磊.云南省高速公路路网风险评价及安全改造[J]．公路交通科技(应用技术版)，2016，(1)：271-272.

[2] 喻卫华，邓永年，邓凯. 浅析高速公路隧道交通安全评价方法[J]．公路交通科技(应用技术版)，2016，(3)：357-360.

[3] 郭延永，刘攀，吴瑶，等.山区高速公路隧道交通运行环境安全评价[J].武汉理工大学学报，2013，35(7)：53-58.

AdissertationonlongtunnelofmountainexpresswaytrafficSafetyevaluationforempiricalanalysisbasedonfuzzytheory

ZHANG Long-sheng1，ZHOU Xiao-yong1，ZHANG Bing2，ZOU Yun-xia3

(1.Jiangxi Transport Consultation Company，Nanchang，Jiangxi 330008，China；2.Jiangxi Transportation Institute，Nanchang，Jiangxi 330200，China；3.Jiangxi Transportation Planning Survey and Design Institute，Nanchang，Jiangxi 330003，China)

This paper mainly analyzes the traffic operation characteristics of long and large tunnel in expressway of Jiangxi province. At first, according to various factors analyzed from the risks of traffic accidents that affect traffic safety, establish an evaluation index system about traffic safety of long and large tunnel in expressway. Then, use Analytic Hierarchy Process and Fuzzy Mathematics Theory to construct comprehensive evaluation model. Finally, use Jiuling Mount tunnel as an example to make an empirical analysis.

tunnel; fuzzy theory; traffic safety evaluation

2016-11-17

张龙生(1966年-)，男，工程师，研究方向：交通工程、地下工程。

江西省交通运输厅科技项目(2015C0012和2014R0011)和江西省青年科学基金项目(20151BAB216024)。

U491

：C

：1008-3383(2017)07-0151-03