基于机械抖动激光陀螺仪的动态误差分析

,,

(哈尔滨工业大学航天学院,哈尔滨 150080)

基于机械抖动激光陀螺仪的动态误差分析

邓亚娇,王振桓,曾庆双

(哈尔滨工业大学航天学院,哈尔滨150080)

机抖激光陀螺仪是目前应用最为广泛的激光陀螺,是实现应用捷联惯导系统进行导航的理想惯性仪表,研究激光陀螺仪的误差因素,并通过软件进行补偿提高其精度,对提高捷联惯导系统的精度具有重要意义。相对于研究已经较为成熟的静态误差,对动态误差的研究仍较少。针对激光陀螺的动态误差,通过分析在动态环境中抖动机构的输出对二频机抖激光陀螺输出的影响,建立了动态误差模型,为激光陀螺动态误差的研究提供了理论储备,具有一定的工程应用价值。

捷联惯导系统;机抖激光陀螺;动态误差;建模

0 引言

惯性仪表是惯性导航系统的关键部件,在很大程度上决定了惯性导航的精度。当惯性仪表长期连续工作时,由惯性仪表输出误差引起的导航误差会随着时间进行累积,据统计在由各种因素引起的总的导航误差中,有70%以上的误差是由惯性仪表引起的[1]。故此,惯性仪表精度的提高是提高导航精度的一条重要途径。

目前,通过对惯性仪表的误差进行分析,建立精确的误差模型,并标定出相应的误差系数,由软件对误差进行补偿来提高惯性仪表精度的方法具有极大的优势。其中,分析仪表误差并建立精确的误差模型是标定的基础。惯性仪表的误差主要包括静态误差、动态误差及随机误差,目前国内外对于静态误差的研究已经趋于成熟,而对于动态误差则研究较少。而对于捷联惯导系统,惯性仪表直接固连于载体之上,没有机械平台的隔离作用,载体的运动会直接作用在惯性仪表上,惯性仪表需承受很大的动态范围。当载体处在激烈的动态环境中时,惯性仪表的内部结构受动态力矩的干扰会使其输出中不可避免地引入动态误差,且不可忽略。因此,研究惯性仪表的动态误差,并对其进行补偿,对提高惯性导航精度具有重要意义。

激光陀螺是一种新型的光学角速率敏感器,是利用激光作为相干光源,采用差频探测技术,由环形激光谐振腔构成的测量角速度或角度的装置,发展成熟于20世纪60年代以后。相对于机械转子陀螺,它具有线性度好、性能稳定、可靠性高、耐振动冲击、寿命长、动态范围广、启动迅速等一系列优势[2-3],使其在在各个领域得到了广泛的应用,在军事领域中的应用尤为突出。目前应用最为广泛的激光陀螺仪为机抖激光陀螺仪,它是实现应用捷联惯导系统进行导航的理想惯性仪表。因此研究机抖激光陀螺仪的误差因素,对提高捷联惯导系统的精度具有重要意义。然而目前大多学者都集中于研究温度[4]和随机噪声对其输出的影响,对其动态误差的研究则相对较少。但当载体处在激烈的动态环境中时,力学环境恶劣,由于机抖机构的存在,动态误差的影响将变得不可忽略[5]。因此,为了研究机抖激光陀螺的动态误差,本文通过分析在动态环境中抖动机构的输出对二频机抖激光陀螺输出的影响,建立了二频机抖激光陀螺的动态误差模型,为激光陀螺动态误差的研究提供了理论储备。

1 机抖激光陀螺的输入输出方程

对于机抖激光陀螺的抖动偏频技术在很多文献中都有阐述,因此这里不再赘述,本文中采用的机械抖动偏频信号为正弦形式,如下所示

ωDB=ωDBMcos(2πfDBt)

(1)

二频机抖激光陀螺的输出为两路正弦拍频信号,相位差为π/2。经过零电平电压转换器,将两路正弦拍频信号转换为两路相位差为π/2的方波信号[6]。当采用式(1)所示的机械抖动偏频信号时,通过对这两路方波信号进行鉴相计数,可得到计数值N的表达式如下[7]

(2)

式中：ω为机抖角频率;φ为机抖相位与陀螺信号中机抖相位的差值;Ω(t)为t时刻陀螺的输入角速度;ε(t)为t时刻的随机误差项。

由式(2)可以看出,计数值N由激光陀螺的输入角速度、抖动偏频引起的正弦振动及随机噪声误差项三部分组成,设定采样时间间隔为Δt,对机抖激光陀螺的输出信号进行采样,可得到第i个采样值ΔNi,具体表达式如下

Ni-Ni-1 =ΔNi

=Asin(ωti+φ)-Asin(ωti-1+φ)+

(3)

式中,根据三角函数和差化积公式,可将由抖动偏频机构引起的正弦振动化为如下形式

Asin(ωti+φ)-Asin(ωti-1+φ)=

当Δt足够小时,可将上式化为如下形式

Asin(ωti+φ)-Asin(ωti-1+φ)≈

AωΔtcos(ωti+φ)

(4)

最终可得第i个采样值ΔNi的表达式

(5)

式中，K=AωΔt。

通过鉴相计数得到陀螺的输出信号后,为得到实际的外部输入角速度,需要对陀螺的输出信号进行解调,即需要去除由抖动信号引起的正弦输出量,目前常用的抖动剥除技术有整周期计数和数字滤波两种方法[7]。采用合适的抖动剥除技术将抖动去除后,最终可得到采样值的理想值

(6)

理论上激光陀螺由于其全固态的结构,动态误差对其影响较小。但对于二频机抖激光陀螺,由于机抖机构的存在使得激光陀螺在角加速度的作用下,输出信号中会引入低频干扰量,这一干扰无法通过抖动剥除技术去除,会对陀螺的最终输出产生影响,使得陀螺的第i个采样值变为如下形式

(7)

式中，β为陀螺工作在动态环境中由抖动机构引入的低频干扰量

据此,本文将通过分析陀螺工作在动态环境中时,由机抖机构引入的干扰信号对陀螺输出信号的影响,来建立机抖激光陀螺的动态误差模型。

2 机抖机构动力学简化模型

抖动机构是二频机抖激光陀螺的关键部件,是保证其正常工作的基本组成部分。通过查阅文献可知,众多学者在研究抖动机构时,通常将其看为一个整体,而不考虑各个部分的分运动。因此,可认为抖动机构只是在围绕其中心轴线做扭转振动,通常可将其等效为如图1所示的一个单自由度扭转振动的质量弹簧阻尼系统来进行研究[8-9]。

图1 等效质量弹簧系统Fig.1 Equivalent mass spring system

根据图1可以建立出系统的振动方程如下

(8)

式中，J为系统总转动惯量；C为系统阻尼项；K为系统总刚度；θ为抖动轴转动角度；M(t)为抖动驱动力矩。

在本文的讨论中采用正弦抖动偏频信号,故此,驱动力矩应为正弦波,表达式如下

M(t)=M0sin(ωdt)

(9)

在式(9)给出的正弦波力矩驱动下,通过解微分方程求取抖动轴转角表达式。首先可将式(8)改写成如下形式

(10)

考虑系统零初值,对式(10)左右两边同时进行Laplace变换,可得θ(s)

(11)

再对式(11)进行Laplace反变换,可求得时域中抖动轴转角的表达式如下

(12)

根据式(12)可知,抖动轴输出的转动角度由稳态响应和瞬态响应两部分组成。在启动机械抖动偏频装置时,启动阶段抖动轴的输出存在过渡过程即体现为瞬态响应,在实际应用中,这一过程很短,系统迅速完成启动过程到达稳态,故可忽略暂态过程的影响,考虑系统的输出只是稳态响应,即

(13)

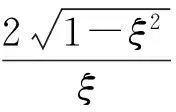
θ(t)=θ0(t)+e-ξωnt[C0cos(ωdt)+

(14)

根据式(14)可知,当系统存在初值时只对瞬态响应部分有影响,改变了系统到达稳态的时间；而稳态响应部分仍与系统具有零初值时相同。由于本文的分析中只需考虑稳态响应,故可认为有无初值对系统的输出无影响,在以后的分析中也不再考虑初值问题。

3 动态环境中机抖机构输出信号对陀螺输出的影响

本节中将根据第2节中得到的机抖机构的动力学简化模型,分析机抖机构在动态环境中的受力状况,重新改写振动输出方程,求取机抖机构的输出转角。根据在动态环境中得到的抖动机构的输出,分析其对陀螺输出信号的影响,建立机抖激光陀螺的动态误差模型。

3.1 抖动轴与输入轴重合时的动态误差模型

图2 抖动机构受力分析示意图Fig.2 Dithering mechanism stress analysis diagram

式(8)需修改为如下形式

(15)

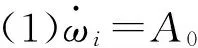
由于正弦驱动力矩产生的稳态响应,在第2节中已经给出,这里只需计算由外部输入力矩的作用使系统产生的稳态响应。通过Laplace变换对式(15)进行求解,可求得机抖机构在时域里的振动输出为

由此可得系统稳态响应为

θ1s(t)=JA0

(16)

由式(13)和式(16)可知,抖动轴输出的角度为

θ(t)=θ0s(t)+θ1s(t)=Acos(ωdt)+JA0

(17)

由式(17)可以看出,由于外部力矩的作用,使得抖动轴输出角度额外叠加了一个常值信号。对激光陀螺输出信号鉴相计数,可得

(18)

在式(18)中可以看出,由外部力矩作用叠加的角度信号对陀螺的输出不起作用,即当外部输入角加速度为常值时,没有在陀螺的输出中引入额外的误差。

通过对式(15)求解,可得抖动轴输出响应

θ2(t)=JA1t-2JA1ξ/ωn+(2JA1ξ/ωn)e-ξωnt·

(19)

其中,稳态响应为

θ2s(t)=JA1t-2JA1ξ/ωn

(20)

由式(13)和式(20)可知,抖动轴输出的角度为

θ(t) =θ0s(t)+θ2s(t)

=Acos(ωdt)+JA1t-2JA1ξ/ωn

(21)

由式(21)可以看出,由于外部力矩的作用,使得抖动轴输出角度额外叠加了一个常值信号和一个斜坡信号。当对激光陀螺输出信号进行鉴相计数时,由之前的分析可知常值信号对陀螺的输出没有影响,而对于斜坡信号

θ(ti)-θ(ti-1) =Ksin(ωdt)+JA1(ti-ti-1)

=Ksin(ωdti)+JA1Δt

(22)

故

Ni=θ(ti)-θ(ti-1)+

=Ksin(ωdti)+JA1Δt+

(23)

对陀螺输出信号采用适当的抖动剥除技术进行处理,去除抖动机构在陀螺输出信号中引入的正弦输出,可得

(24)

(25)

考虑抖动机构的振动输出方程,变为如下形式

=M(t)+J·f(t)

=M(t)+J·[f0(t)+f1(t)+

f2(t)+…+fj(t)+…]

(26)

对函数f(t)的每一段进行分析,t∈(tj,tj+δt]时,f(t)=fj(t)=aj+bjt,此时抖动机构振动输出方程形式如下

(27)

对式(27)求解微分方程,可得到抖动轴输出角度稳态响应

(28)

对激光陀螺输出信号鉴相计数时

θj(ti)-θj(ti-1) =Ksin(ωdti)+JbjΔt

=Ksin(ωdti)+J·fj′(t)Δt

(29)

考虑整个时域范围时,可得到θ(ti)-θ(ti-1) =Ksin(ωdti)+J·[f0′(t)+f1′(t)+

f2′(t)+…fj′(t)+…]Δt

=Ksin(ωdti)+J·f′(t)Δt

(30)

(31)

3.2 抖动轴与输入轴不重合时的动态误差模型

当抖动轴与陀螺输入轴不重合时[10],抖动轴受到的外部力矩将不只与沿陀螺输入轴方向的角加速度有关,还与沿同输入轴方向正交的两轴方向的角加速度有关。由此,在动态环境中抖动机构在陀螺输出信号中引入的动态误差将不再只有一项。

(1)抖动轴为刚性轴

当抖动机构坐标系与陀螺坐标系之间存在失准角时,两坐标系的位置关系如图3所示。

图3 抖动机构坐标系与陀螺坐标系位置关系Fig.3 Relation between dithering mechanism coordinate and gyro coordinate

图3中,g坐标系为陀螺坐标系,d坐标系为抖动机构坐标系。

沿抖动轴方向不仅有输入轴方向的角加速度,同时在该方向也引入了另外2个正交方向的角加速度。

(32)

(33)

(34)

K1=Jcosθocosθs

K2=Jθscosθocosθs

K3=Jθocosθocosθs

最终得到机抖激光陀螺的动态输出误差模型如下

(35)

其中：K1=Jcosθocosθs

K2=Jθscosθocosθs

K3=Jθocosθocosθs

(2)抖动轴具有挠性

当抖动轴具有挠性时,在与输入轴方向正交的两轴方向施加角加速度,会使抖动轴发生弯曲。设沿输出轴方向转过角度θo,沿S轴方向转过角度θs,抖动轴偏转前的初始坐标系为o-ios,偏转后的坐标系为o-i′o′s′,2个坐标系的位置关系如图4所示。

图4 抖动轴偏转前后坐标系位置关系Fig.4 Relation between dithering axis coordinate before and after the deflection

在这里抖动轴的受力方向应为沿与输入轴方向正交的两轴方向,考虑在沿O轴的力矩作用下,抖动轴偏转了θo角度。由于θo为小量,S轴方向与S1轴方向十分接近,故近似地认为另一个力矩方向沿S1轴方向。所以可以认为,抖动轴在沿S1轴方向力矩的作用下偏转了θs角度。最终,抖动轴与输入轴之间的偏角为θ,且cosθ=cosθocosθs。

根据图4所示,可求得2个坐标系之间的转换矩阵,从而可求得在抖动轴偏转后得到的坐标系o-i′o′s′中沿抖动轴方向的输入角加速度

(36)

由于在本质上挠性支撑类似于一个弹簧系统,这里忽略重力的影响,因此,该运动过程的运动方程可写为如下形式:

(37)

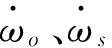
(38)

θoj=Jocj+Jodjt-2Jodjξ1/ωn1

(39)

考虑整个时域,可得θo=Jo[(c0+d0t)+(c1+d1t)+…+(cj+djt)+…]-

2Jo(d0+d1+…+dj+…)ξ1/ωn1

=Jo[g0(t)+g1(t)+…+gj(t)+…]-

2Jo[g0′(t)+g1′(t)+…+gj′(t)+…]ξ1/ωn1

=Jog(t)-2Jog′(t)ξ1/ωn1

(40)

根据式(40)同理可得θs的表达式如下

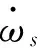
(41)

(42)

将式(42)代入到抖动机构的振动输出方程中,可得

(43)

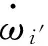
(44)

最终可以得到,当抖动轴具有挠性时的机抖激光陀螺的J态输出误差模型如下

(45)

其中:

K1=J，K2=J(Js-Jo)

K3=J(Js-Jo)，K4=-2J(Js-Jo)ξ1/ωn1

K5=-2JJsξ1/ωn1，K6=2JJoξ1/ωn1

4 结论

本文通过分析在动态环境中机抖机构的输出对激光陀螺输出的影响,建立了二频机抖激光陀螺的动态误差模型,为后续研究机抖激光陀螺的动态误差提供了理论储备。但在模型建立时仅考虑了抖动机构沿抖动轴方向受到的力矩对抖动机构输出的影响和抖动轴为挠性支撑的影响,而未考虑其他未知因素,因此该模型的建立并不完整且存在一些由近似引入的偏差,还有待进一步完善。

[1] 程源.激光陀螺捷联惯性组合的标定方法研究[D].哈尔滨: 哈尔滨工业大学, 2010.

[2] 査峰, 高敬东, 许江宁, 等.光学陀螺捷联惯性系统的发展与展望[J].激光与光电子学进展, 2011，48(7): 33-40.

[3] Faucheux M, Fayoux D, Roland J J.The ring laser gyro[J].Journal of Optics(Paris), 1988, 19(3): 101-115.

[4] Zhang Y, Guo Y, Li C, et al.A new open-loop fiber optic gyro error compensation method based on angular velocity error modeling[J].Sensors, 2015,15(3): 4899-4912.

[5] Li H, Pan Q, Wang X, et al.A dynamic attitude measurement system based on lins[J].Sensors, 2014,14(9): 16082-16108.

[6] 粟荣涛.二频机抖激光陀螺信号的高速采集与处理[D].长沙: 国防科学技术大学, 2010.

[7] 温锋, 李锦明, 杨阳, 等.一种新型高效的激光陀螺抖动信号剥除技术研究与实现[J].计算机测量与控制, 2014, 22(1): 207-209.

[8] 张维娜.机抖激光陀螺机电特性分析与建模[D].长沙: 国防科学技术大学, 2009.

[9] Chen G, Rui X, Yang F, et al.Study on the dynamics of laser gyro strapdown inertial measurement unit system based on transfer matrix method for multibody system[J].Advances in Mechnical Engineering, 2013(5): 1-9.

[10] Li G, Wu W, Fan Z, et al.Research of misalignment between dithered ring laser gyro angle rate input axis and dither axis[C]//Proceedings of the International Symposium on Optoelectronic Technology and Application,International Society for Optics and Photonics,2014: 92971 X-92971X-6.

DynamicErrorAnalysisBasedontheDitheredLaserGyro

DENGYa-jiao,WANGZhen-huan,ZENGQing-shuang

(SchoolofAeronautics,HarbinInstituteofTechnology,Harbin150080,China)

Mechanically dithered ring laser gyroscope, which is most widely used, is the ideal component for strapdown inertial navigation system, thus the research and compensation of laser gyroscope error factors by the software are of great significance for improving the precision of the strapdown inertial navigation system.Compared to static error, the study of dynamic error is still inadequate worldwide.For the dynamic errors of laser gyro, the influence of dithering mechanism output on the mechanically dithered ring laser gyro output in the dynamic environment is analyzed, and the dynamic error model of ring laser gyro is set up.The research finding provides a good reference for the study of the dynamic error of laser gyro and has certain engineering application value.

SINS; Mechanically dithered ring laser gyro; Dynamic error; Modeling

2017-06-01；

：2017-07-11

：国家自然科学基金(61640301)

：邓亚娇(1993-)，女，硕士，主要从事导航、制导与控制方面的研究。E-mail:1540107297@qq.com

10.19306/j.cnki.2095-8110.2017.05.013

V241.6

：A

：2095-8110(2017)05-0075-08