基于关联度分析的生产异常模式挖掘
李春生,宋 佳,张可佳,张 勇
(东北石油大学 计算机与信息技术学院,黑龙江 大庆 163318)
基于关联度分析的生产异常模式挖掘
李春生,宋 佳,张可佳,张 勇
(东北石油大学 计算机与信息技术学院,黑龙江 大庆 163318)
为解决在智能化生产预警方法应用的过程中原始数据维度高、数据结构复杂、数据量大的问题,提出了基于关联度分析的生产异常模式挖掘方法。该方法建立了预警目标与影响特征之间的关联关系,通过计算关联度筛选出重要特征。在均值化方法处理数据的过程中,通过引入时间序列、选取时间粒度来截取距离数据,通过计算关联度、摒弃无效影响特征和降低数据维度来完成数据的准备过程。结合损耗性异常的业务数据特点,采用了基于时间序列的G-R分段拟合方法拟合数据,并利用均方根误差方法校验模型的准确性。实验验证选取了三次采油生产的异常情况为实例,采用G-R模型对特征集的元素进行分段拟合以求解相关参数。实例验证结果表明,该方法的预测数据与原始观测数据的吻合度高,且预测准确度较高。
特征筛选;时间序列;函数拟合;关联分析
0 引 言
随着工业生产预警研究的不断深入、监测手段的广泛应用以及数字化生产的进步,工业生产领域中的异常情况已经逐渐成为各领域研究的重点,运用智能技术挖掘数据内部潜在规律,提取有用信息已成为动态监测、分析异常、预警预测的关键[1]。
通过专家经验的累积和较强的业务能力,虽然能较为准确地掌握对生产异常的影响特征,但是这种人工决策方法具有如下缺点:仅依据业内专业人才定义有效影响特征集,降低了挖掘结果的准确性;累积数据量大,特征集维度高,非敏感特征的隐蔽性强[2],敏感特征表现不明显;数据项的拟合算法简单,只采用一种拟合方法在高阶拟合处理方面具有一定的难度,计算结果不够精确[3]。
针对上述问题,提出了基于关联度分析的生产异常模式挖掘方法,建立了预警目标与影响特征之间的关联关系,计算关联度,筛选出重要特征。在均值化方法处理数据的过程中,引入时间序列,降低数据分析过程中的耦合度,增强数据处理的精细程度;结合业务特点[4],选取多种时间粒度,按不同粒度截取距离数据。通过对特征集散点图数据的分析,采用基于时间序列的G-R分段拟合方法拟合数据,得到拟合矩阵,同时用均方根误差方法校验模型的准确性,提高挖掘结果的可信度,完成有效特征筛选及生产预警的过程。
1 基于关联度分析的特征子集的获取
通过建立预警目标与影响特征之间的关联关系,计算关联度,筛选出有效影响特征子集。关联分析的具体步骤为:原始特征集的获取、特征集的逻辑转换、基于均值化的分段式时序数据处理。
1.1原始特征集的逻辑转换
原始特征主要分为静态物性特征、骤发性异常特征、损耗性异常特征,其中静态物性特征通常用来描述预警对象的基础属性,长期不发生变化,骤发性异常具有不可控性,所以在此主要研究在损耗性异常特征情况下预警目标与特征集之间的变化关系。
原始特征集构成了数据有序化的信息集合,是筛选有效特征的构建基础。针对预警目标,选取特征集,具体表达结果如下:
(1)设定预警目标I、与预警目标相关的原始影响特征集合Un:
I={I1,I2,…,In}
Un={Un1,Un2,…,Unm}
其中,n表示预警目标数量;Unm表示针对预警目标In的影响指标;m表示影响预警目标In的影响因子数量。
(2)在完成原始特征集的筛选后,需要获取特征集的全部数据,在此提出SF模型,实现建立自然语言与数据体内数据实体间的映射关系,定义如下:
定义:包含预警目标的自然语言描述I,针对预警目标I的影响指标的自然语言描述U,直接描述U的数据实体S及映射关系函数F的闭包结构成为SF模型。其一般表示形式为:
SF={I,U,S,F|U∈Un,I∈I,S≠∅,n≥1}
其中,S为数据实体,实例化后为数据体内的数据单项;Un为针对预警目标I收集的原始影响指标数据集;F为映射关系函数,当S为数据体的直接映射时,F为空,当S为数据体的间接映射时,S由函数F计算。
以SF模型对Un进行逻辑转化,得到原始闭包集FU,其表达形式如下:
FU={SF1,SF2,…,SFP|P=len(Un)}
1.2处理数据中时间粒度的引入
由于原始数据的复杂性,量纲差异性大,导致各指标间的综合性差,不能直接进行分析。目前消除量纲差异的方法主要有极值化方法、标准方法、均值化方法[5]。其中,极值化方法只依赖变量中的最大值和最小值;标准化方法在消除量纲差异的同时,还消除了各个变量在变异程度上的差异性;均值化方法在消除量纲差异的同时,保留了各变量取值的差异程度[6]。所以采用均值化方法对数据进行无量纲化处理。
在均值化处理原始数据的过程中引入时间序列[7],选取时间粒度。时间粒度选取的不同会给数据挖掘带来不同的难度。图1分别显示了不同时间粒度聚类得到的时间序列。从上到下依次是按天聚类、按周聚类、按月聚类。
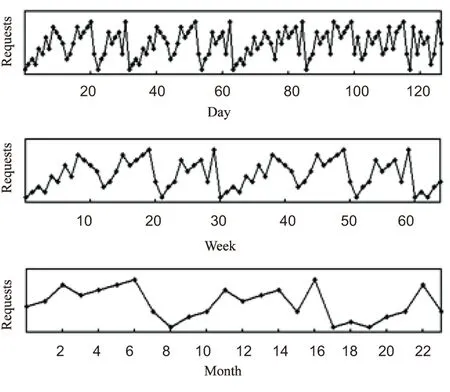
图1 不同时间粒度的时间序列
由图可知,时间粒度选取得越大,每个时间点上的请求量就越大。
对于大的时间粒度,数据基数大,能提供较为详尽的数据,但在查询过程中需要较多的时间以及存储空间[8]。对于小的时间粒度,数据基数较小,能提高查询效率以及占用较小的存储空间,但是却不能提供详尽的数据。
所以在时间粒度选取的过程中,从以下两方面来考虑:第一,根据业务特点了解数据类型,分析数据特点,选取时间粒度;第二,根据数据特点,明确可接受的数据最低粒度以及能够存储的数据量。
1.3基于均值化的分段式时序数据处理
结合生产预警数据的呈现特点,引入同一模式多重粒度的思想[9],即近期的生产数据按大粒度选取综合数据,比较久远的生产数据按小粒度保留汇总数据,解决了大粒度选取提取数据基数大、占用较大存储空间,小粒度选取数据准确率低的问题。
工业生产数据主要分为数值型数据和符号型数据。符号型数据主要描述某数据对象的基础信息,包括机型、作业位置、层位等信息,反映的是其与全集间的隶属关系,不存在逻辑运算过程;数值型数据,反映了特征的隐蔽性和交叉性[10],在此提出了均值化分段式时序方法处理数值型数据。关联度分析具体处理过程如下:
Begin:预警目标In触发
Step1:给定时间序列,将集合内的数据实体SFp以及预警目标I按同一模式不同粒度的思想,将近期数据以及久远的异常发生周期的数据按照大粒度分别截取m段,将久远的生产数据按照小粒度截取f段。
T1={t1,t2,…,tm}
T2={t1,t2,…,tf}
Step2:定义tm={tm1,tm2,…,tma}、tf={tf1,tf2,…,tfb}内的预警目标以及影响特征集合,分别表示如下。
预警目标基于给定时间序列的数据集合:
Im={im1,im2,…,ima}
If={if1,if2,…,ifb}
影响特征基于给定时间序列的数据集合:
Sm={sm1,sm2,…,sma}
Sf={sf1,sf2,…,sfb}
其中,a为大粒度截取的数据Im、Sm的长度;b为小粒度截取的数据If、Sf的长度。
Step3:定义预警目标以及影响特征生成的新的局部距离数据集合iu、su。
iu={{im1,im2,…,ima},{if1,if2,…,ifb}}
su={{sm1,sm2,…,sma},{sf1,sf2,…,sfb}}
Step4:将集合iu、su表现形式统一化。转换成新的数据表现形式。
iu={iu1,iu2,…,iud|d=a+b}
su={su1,su2,…,sud|d=a+b}
Step5:原始数据均值处理。如果a>0,b>0,分别计算包括预警目标和特征集合的原始数据的均值。
Step6:基于均值化的距离数据处理。首先对每一个数据项进行均值化处理,再将原始数据集处理为局部距离数据。对预警目标以及特征集均值化的处理结果为:

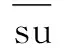
集合iu、su生成基于均值化的局部数据集合:

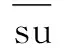
Step7:SFp的数据处理结果为:

D2={T2,iu},T2={t1,t2,…,tf}

Step8:取局部距离数据的均值。
Step9:计算均值化后预警目标In与特征SFp的协方差矩阵。
rd=V/iσdsσd

将协方差和标准差带入,计算关联系数:
rd=
并且-1≤rd≤1,当该数值的绝对值越大,表示相关性越强;当rd=0,表示预警目标与该影响特征不相关;当rd>0,表示两者之间正相关,反之,则负相关。
Step11:计算关联度。
上一步中得到的相关系数表示每个具体数据项与预警目标之间的关系,为了解数据序列整体上的关联程度,计算关联系数的平均值。
Step12:数据处理结果。
根据关联系数反映出的关联度,初步筛选出针对预警目标的粗糙原始影响特征,则筛选出的粗糙原始影响特征集合表示如下:
Un={OUn1,OUn2,…,OUnk|k End 经过上述步骤,完成基于均值化的分段式时序数据处理,对比分段处理前后数据特点可知,原始数据基数大、差异小、数量多、精度低,处理后局部距离数据基数小、差别大、数量适中、精度较高[11]。 数据变化模式的最优计算方法是数值拟合参数计算。基于损耗性异常情况下各特征对预警目标影响的研究,通过对大量实验数据的处理以及数据点的散点图分布,发现曲线比较平滑,呈正态分布,所以最终提出以高斯-瑞利模型(用G-R表示)分段拟合数据点。其中,高斯函数是标准的正态函数[12],瑞利函数描述平稳窄带的高斯过程[13],二者分段拟合数据。 2.1G-R函数的分段拟合 截取上述方法中获取的距离数据su,其离散点分布如图2所示。 图2 距离数据与时间序列拟合曲线 当预警目标I触发,分析特征集内特征:随着时间序列的推移,该特征整体呈下降趋势,最大峰值处于tmax,在tmax至tf区间,曲线呈平缓下降趋势,达到时间点tf之后,曲线下降趋势更加缓慢,将tf至td区间作为函数余音。在tmax至tf区间用高斯函数处理;tf至td区间采用瑞利函数处理。分段拟合函数的表达式为: 由拟合参数构成的参数集V={a,b,c,σ},并以{T1,iu}进行拟合,逐一对满足该模型元素SFp进行参数求解,得到:Vr={ar,br,cr,σr}。其中,r是满足G-R模型的元素数量。Vr合并得到特征矩阵: 该模型实现了对阶段连续数据的分段拟合,在提高拟合精度和效果的同时,减小了拟合误差。通过连续曲线反映出的特征数据点与时间序列间的关系,发现数据内部之间的潜在关系,提取有用信息,为生产预警提供准辅助决策。 2.2模型校验 获得预测结果后,通过计算相对误差及均方根误差校验模型的准确度。根据距离偏移误差公式得: ψd=F(Td)-iud 其中,ψd表示在某时间点Td,预期结果F(Td)与实际样本值SF的偏移差。 均方根误差为[14]: 通过RMSEd的值,反映预测数据偏离真实值的程度,作为验证该模型的准确性。RMSEd越小,表示测量精度越高。当数据偏差较大时,根据Un集取样,重新拟合计算并校正模型结果以实现自适应过程。 以三次采油数据为基础,通过分析油田施工后的生产数据、综合数据以及相关作业的历史数据,挖掘油田生产过程中的生产异常情况,并研究针对生产异常情况的影响特征的变化规律和模式。以油井日产油生产异常为例,完成有效特征集的筛选以及模式挖掘的过程。具体处理过程如下: (1)预警目标I={日产油},收集与预警目标相关的原始项目集合,包括开发动态数据库、开发静态数据库、井下作业数据库、采油管理数据库中的项目集合200余项,这里主要研究损耗性异常情况下特征的变化情况,所以去掉骤发性异常特征以及静态物性特征,筛选得到数据项100余项。 (2)特征集逻辑转换。建立特征集与数据实体之间的映射关系,如表1所示。 表1 基础特征库信息表 (3)选取时间粒度。选取2010-2016年的数据作为基础数据。根据影响因子U与数据实体S的映射关系F,引入时间序列,截取数据粒度,近三年期数据按照大粒度截取,久远的数据按照小粒度截取,即大粒度截取每天的综合数据,小粒度截取每月的汇总数据: T1=Y2010,13,m=36 T2=Y2014,16,m=940 (4)计算关联度。利用基于均值化的关联分析的方法建立影响特征与数据体内数据实体之间的关联关系,引入均值化方法计算影响特征与预警目标之间的关联度。通过计算关联度大小,决定各个特征之间的关联程度,剔除完全不相关特征,得到特征项80项。 经过特征筛选,最后得到重要特征集共计16项。 日产油的重要特征子集构成如下: Un={含水,套压,沉没度,聚合物用量,采聚浓度,采出程度,砂岩厚度,有效厚度,泵径,加砂量,油压,日产液,渗透率,液面深度,泵效,流压} (5)根据G-R模型对特征集的元素分段拟合对参数进行求解,参数计算结果构成的矩阵表现如下: 将参数带入G-R模型,分段拟合,结果见表2。 表2 G-R模型预测结果 表2给出了G-R模型的预测结果以及以相对误差和均方根误差作为评价指标的计算结果,从评价指标来看,G-R模型取得了较精确的预测效果。 G-R模型的含水数据拟合曲线如图3所示。 图3 G-R拟合值与实际值的比较 通过与原始观测数据的对比,发现拟合数据与原始数据吻合度很高,说明G-R模型的可信度很高。 (6)根据设定的预警目标及筛选出的有效特征集,监测某一区块内20余口井一个月内流压,聚合物用量,含水等数据项与日产油的变化情况。应用效果如表3所示。 表3 日产油异常情况 其中,约85%口井的预测情况与实际情况的结果保持一致。由此,上述步骤中的特征筛选及G-R分段拟合模型可以应用在油田生产异常预警领域。 为实现深度挖掘数据内部潜在规律,加强生产异常状况分析,提高挖掘准确率,提出了基于关联度分析的生产异常模式挖掘方法。以SF闭包模型表示自然语言与数据实体之间的映射关系,完成特征集的逻辑转换,采用均值化方法处理基于粒度划分的分段式时序原始数据,降低数据维度,建立预警目标与影响特征之间的关联关系,根据关联度的计算结果剔除完全不相关特征,实现数据的预处理过程。同时分析各特征数据点的散点图分布情况,选定G-R模型拟合数据,得到拟合矩阵,利用均方根误差方法验证了该方法的准确性,提高了挖掘结果的可信度。 [1] 刘立坤.海量文件系统元数据查询方法与技术[D].北京:清华大学,2011. [2] 王 虹,张文修,李鸿儒.粗糙模糊集的不确定性度量[J].计算机工程与应用,2005,41(2):51-52. [3] Deng Xiaoming,Wu Fuchao,Wu Yihong.An easy calibration method for central catadioptric cameras[J].Acta Automation Sinica,2007,33(8):801-808. [4] 王晓鹏,武 彤.生产质量控制数据仓库模型设计与实现[J].计算机技术与发展,2015,26(6):181-184. [5] 严导淦.量纲分析及其应用[J].物理与工程,2012,22(6):22-26. [6] 李 莉,孙永霞.基于均值化主成分分析的雾霆环境分析与研究[J].计算机应用研究,2015,32(5):1373-1375. [7] Sun Haishun,Li Jiaming,Li Jinghua,et al.An investigation of the persistence property of wind power time series[J].Science China (Technological Sciences),2014,57(8):1578-1587. [8] 李春生,邸京华,李少龙,等.时序化生产预警有效影响因子的获取方法研究[J].计算机技术与发展,2016,26(7):122-126. [9] 王 虎,丁世飞.序列模式挖掘研究与发展[J].计算机科学,2009,36(12):14-17. [10] 谢永芳,胡志坤,桂卫华.基于数值型数据的模糊规则快速挖掘方法[J].控制工程,2006,13(5):442-444. [11] 张可佳.基于混合智能的聚驱区块生产动态预警方法研究[D].大庆:东北石油大学,2016. [12] 翟继友,张 鹏.高斯混合模型参数估值算法的优化[J].计算机技术与发展,2011,21(11):145-148. [13] Abdalroof M S,Zhao Zhiwen,Wang Dehui.Statistical inference for the parameter of rayleigh distribution based on progressively type-i interval censored sample[J].Communications in Mathematical Research,2015,31(2):108-118. [14] Wang H B,Wang Y,Fang J,et al.Simulation research on a minimum root-mean-square error rotation-fitting algorithm for gravity matching navigation[J].Science China:Earth Sciences,2012,55(1):90-97. Abnormal Production Pattern Mining Based on Relevancy Analysis LI Chun-sheng,SONG Jia,ZHANG Ke-jia,ZHANG Yong (College of Computer and Information Technology,Northeast Petroleum University,Daqing 163318,China) In order to solve the problem of high original data dimension,complex data structure and large data volume in the process of application of the intelligent production alarming method,a mining method of abnormal production pattern based on relevancy analysis is proposed.It establishes the incidence relation between early warning target and influential characteristics and screens out important features through relevancy calculations.In the process of data processing by equalization method the distance data is extracted by introduction of time series and selection of time granularity and preparation process of data is completed by calculation of relevancy,elimination of invalid influential features and reduction of data dimension.Combined with the data characteristic of abnormal loss,the G-R segmentation fitting method based on time series to fit the data and root mean square error method to verify the accuracy of the model.In the process of experimental verification,the abnormal situation of tertiary recovery production is taken as an example and the G-R model is adopted to carry on segmentation fitting towards the elements of the feature setting for solution of relevant parameters.The experimental results show that the proposed method agrees well with the original observation data,and its prediction accuracy is high. feature selection;time sequence;function fitting;relevancy analysis 2016-08-17 :2016-11-23 < class="emphasis_bold">网络出版时间 时间:2017-07-05 黑龙江省自然科学基金面上项目(F2015020);黑龙江省教育科研规划重点课题(GJB1215013);黑龙江省2016年教育科研课题(16Q117) 李春生(1960-),男,博士,教授,博士生导师,研究方向为人工智能及其应用、模式识别与人工智能;宋 佳(1991-),女,硕士研究生,通讯作者,研究方向为数据挖掘技术。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1650.036.html TP301 :A :1673-629X(2017)09-0124-05 10.3969/j.issn.1673-629X.2017.09.0272 G-R分段拟合模型的提出
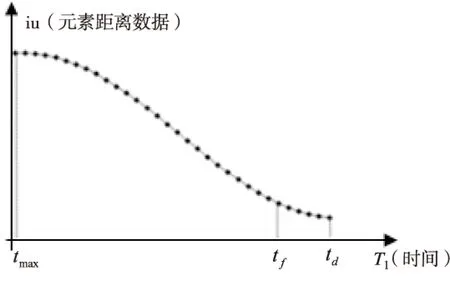
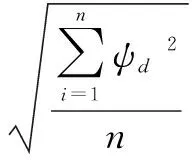
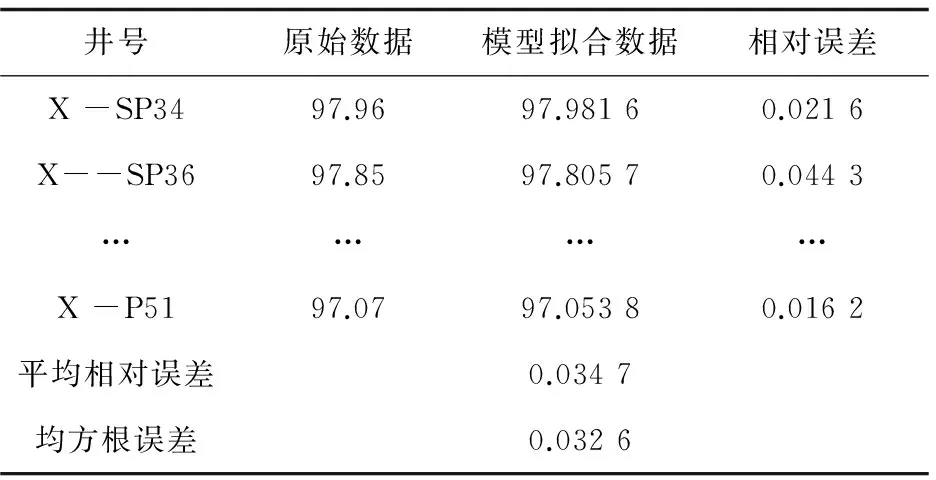
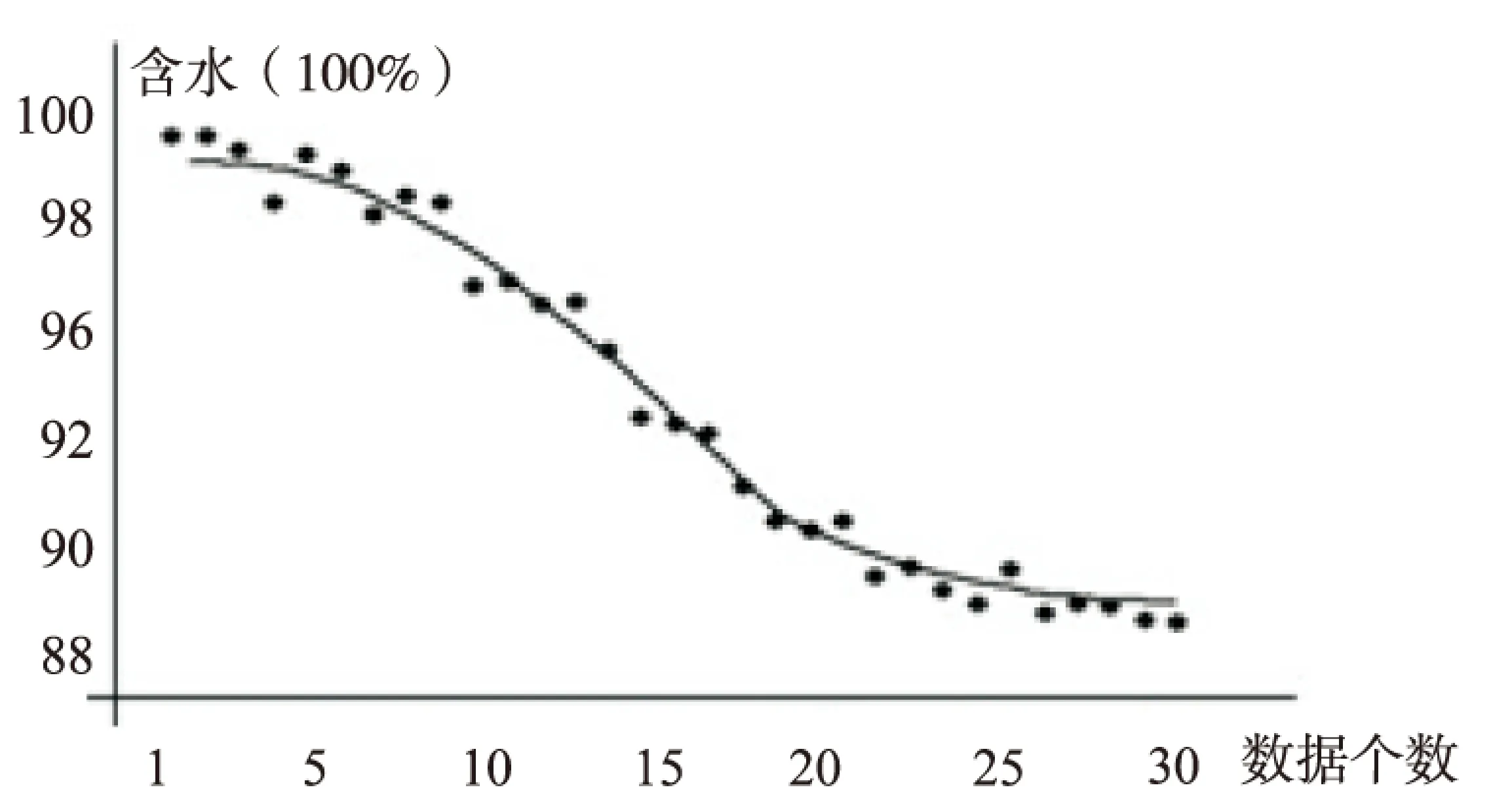
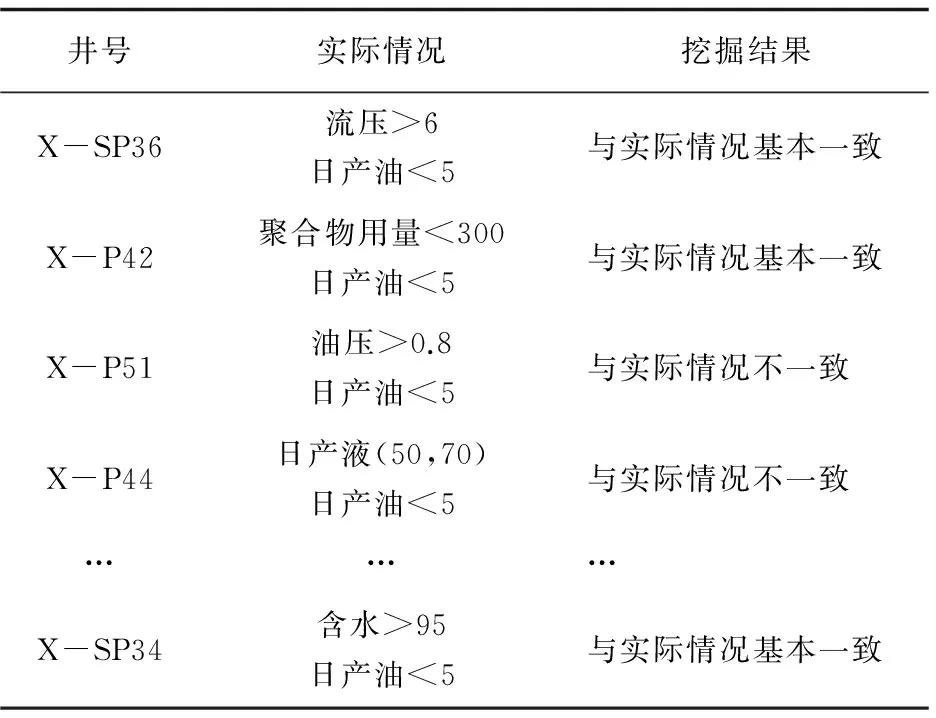
3 设计实例

4 结束语

