基于故障模型的树状直流系统暂态量求解方法

徐 岩， 刘婧妍

(新能源电力系统国家重点实验室(华北电力大学)，河北 保定 071003)

基于故障模型的树状直流系统暂态量求解方法

徐 岩， 刘婧妍

(新能源电力系统国家重点实验室(华北电力大学)，河北 保定 071003)

当多端VSC系统线路发生极间短路故障时，多个VSC(Voltage Source Convert)站共同作用，故障特性相当复杂，而单端VSC系统的故障特性表达式很容易得到，因此提出将故障模型按照端数进行分解。研究对象为3端树状直流系统，将3端系统电容放电过程分解为3个单端电容单独作用过程，分析出单端故障模型与多端故障模型之间参数的关系表达式，通过对单端故障模型暂态表达式的求解得到最终结果，进一步研究参数的改变对故障特性的影响。此方法大大简化了计算量，可以拓展到更多端，具有普遍适用性，通过MATLAB/SIMULINK验证了方法的有效性，为故障定位和保护方法的研究提供了理论依据。

树状直流系统； 故障模型的分解； 故障特性； 极间短路故障

0 引言

为了实现直流配电网与目前交流电网的对接，基于全控型电力电子变流器的多端柔性直流系统成为重要发展方向[1-2]。多端柔性直流系统是采用多个整流站和多个逆变站的直流系统，它不仅能以多个分布式送端电源共同供电以满足供电容量的需求，同时能以多个分散式受端落点来共同消纳功率从而降低故障时受端交流系统所受的冲击，与传统双端柔性直流系统相比，多端柔性直流系统在运行方式、电能分配和控制方面都更为灵活、方便[3]。制约多端柔性直流系统可行性的关键技术即为保护技术，而故障特性的研究是研究保护问题的基础。

根据故障发生的区域不同，柔性直流系统的故障可以分为3类：换流变压器交流侧故障、换流变压器阀侧故障和直流系统侧故障。直流系统侧故障中直流线路故障发生概率为80%，直流线路故障类型包括单极接地故障、断线故障和正负极间短路故障，其中后者危害最为恶劣[4]。

文献[5,6]详细研究了双端VSC直流线路的3种故障的故障特性。文献中提到直流侧发生极间短路故障时会经历3个阶段：直流侧电容放电阶段，二极管续流阶段和交流电源作用下的稳态阶段。由于当多端VSC线路发生故障时，等同于多个VSC站共同作用的结果，因此故障特性相当复杂，故障电流的升高速度较双端的更快，更具有危险性。文献[7]中提到了多端VSC的故障特性，也可以像双端VSC一样，分为以上3个阶段，故障特性的阶段性与故障位置无关[8]。由于工程实际中，保护必须在达到临界时刻即直流电压降为零之前可靠动作，即电容放电阶段，因此着重对电容放电阶段的暂态过程进行分析。

首先对多端柔性直流系统的极间短路故障暂态量表达式进行求解，主要研究电容放电阶段，通过求解状态方程，利用分解的思想，推导出了故障发生后直流电压、直流电流的暂态表达式。在此基础上进一步探讨故障线路参数对故障特性的影响。最后，通过MATLAB仿真软件，对理论分析进行了验证。

1 树状直流系统的双极短路故障

1.1单端系统故障等效模型

直流系统发生双极短路故障时，会经历3个阶段：直流侧电容放电阶段、二极管续流阶段和交流电源作用下的稳态阶段。单端送电的直流系统，在故障发生瞬间，由于电容器的快速放电，使直流电压减小的同时直流电流增大，此时直流侧电容、线路电感以及电阻组成1个串联RLC二阶电路，由电路KVL可得：

(1)

RLC二阶电路中，电容为C，电容两端电压为Vdc，电阻为R′，电感为L′，流过线路电流为IL。

假设在t0时刻直流系统发生双极短路故障，对此二阶电路的欠阻尼过程进行求解[9-10]，得出故障后直流电压和直流电流的暂态表达式为：

(2)

(3)

树状结构主要用于直流配电网，将直流电压在用户侧降至用户负荷要求的电压等级。树状拓扑结构，如图1所示。

图1 直流系统的拓扑结构图

由于工程实际的要求，电容放电阶段的暂态过程对系统的安全运行至关重要。研究的多端系统各端参数均一致，针对其他情况，此方法也适用。此阶段的电路图可由图2等效。

图2 电容放电阶段等效电路图

根据图2的故障等效模型，列写多端系统的状态方程，但多个状态变量求解相对复杂。而单端系统的故障特性求解要简单很多，因此将故障模型进行分解。

2 故障模型的分解

本文提出的分解的思想是借鉴了叠加原理，但是并不是完全相同。因为电容是储能元件，它不能单单看成是电流源亦或是电压源，本文将其做断路处理是因为在直流系统稳定情况下，该元件是以断路的形式存在的，只是电压存在初值。因此本文进行分解时，将该元件赋予初值，与故障发生时刻完全等效。多端VSC直流系统发生极间短路故障时，电容放电阶段的多端共同作用可以分解为各端单独作用。一端单独作用时，其他端电容相当于断路状态。当网络内部发生故障时，n端作用结果可分解为图3中各端作用。

图3 第i(i=1,2,…，n)端的VSC单独作用的网络结构图

对于图2所示电路，应用分解思想，给出电容放电阶段电流流向示意图，以VSC1端单独作用为例，如图4所示。

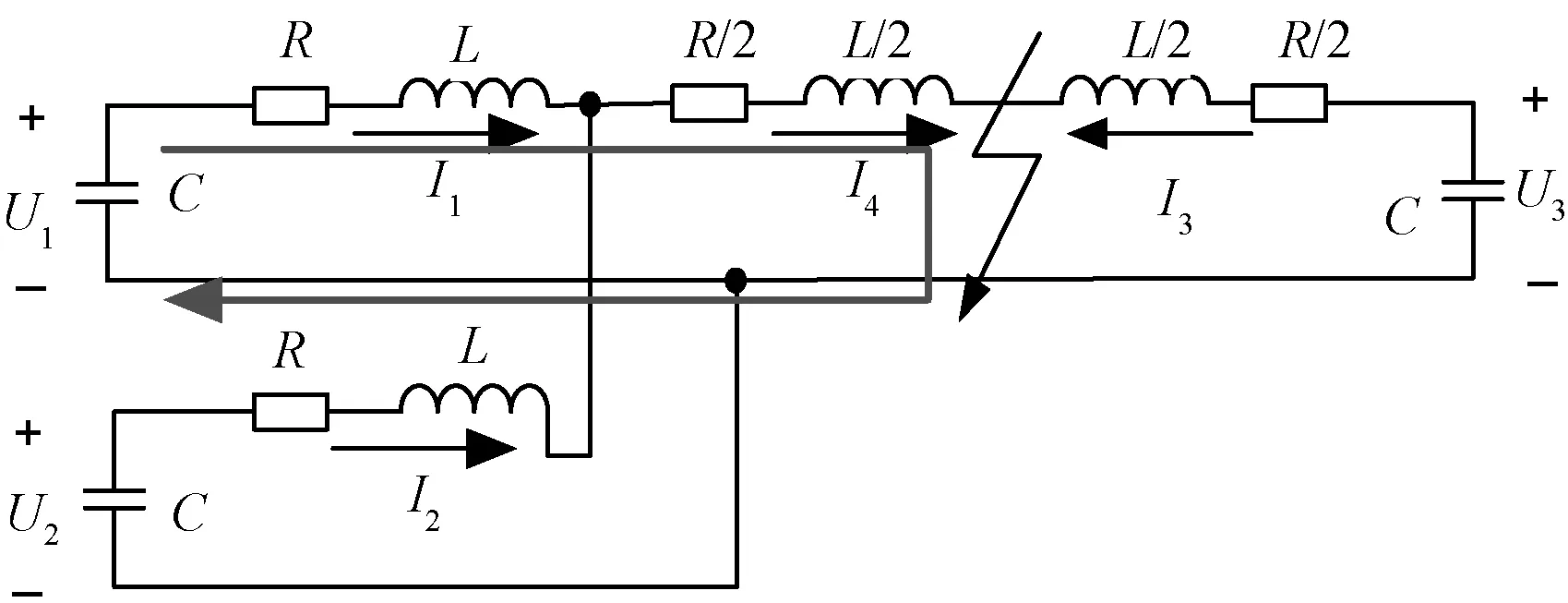
图4 VSC1端单独作用时电流流向示意图

根据图4中的电流流向，可以得到VSC1单端作用时的等效电路图，电流所走路径为箭头标识的部分，如图5中的(a)，其余两端单端作用时的等效电路图分别如(b)、(c)。

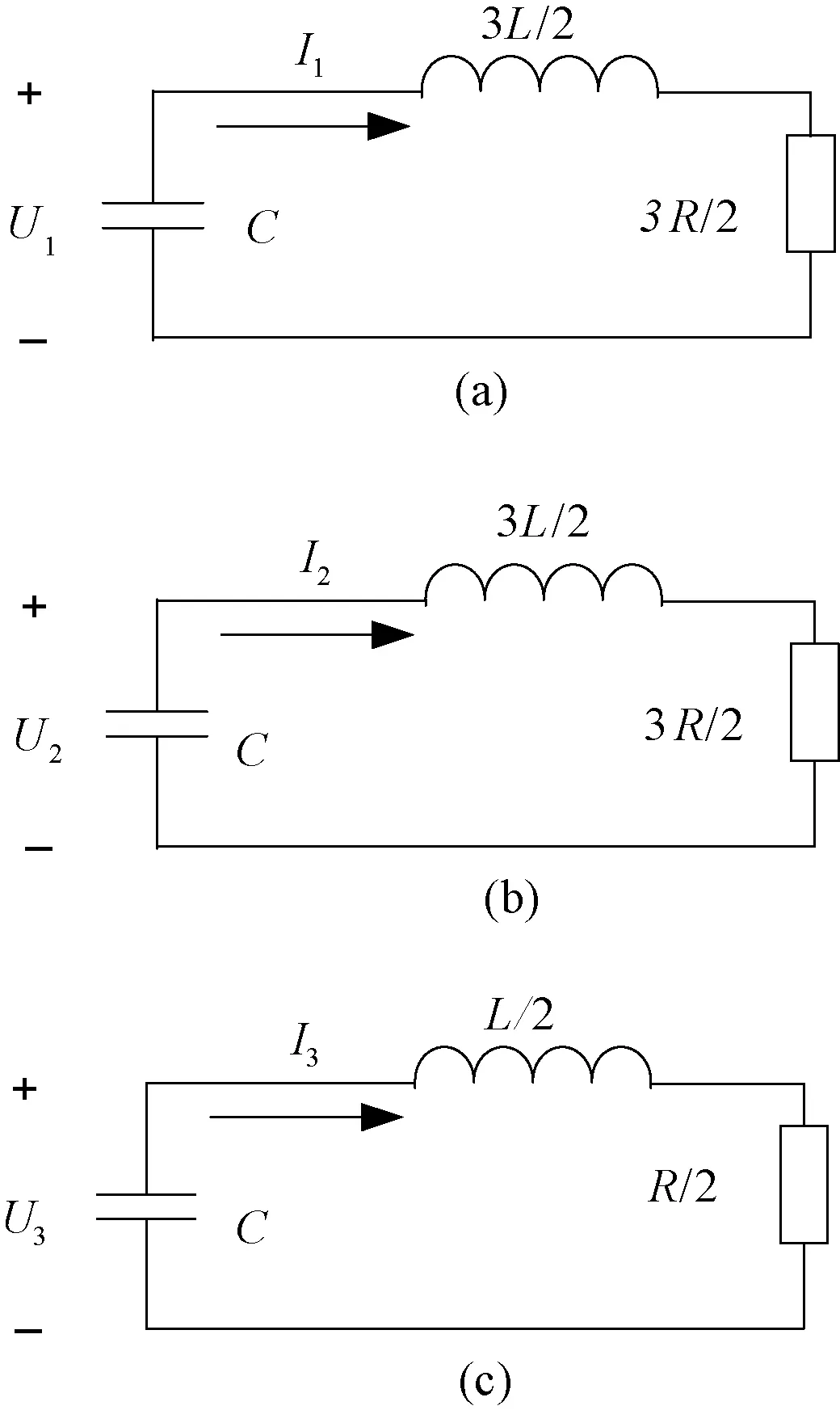
图5 电容放电阶段各端作用等效电路图

图5(a)，(b)和(c)分别是3个RLC二阶振荡电路图，将参数直接代入公式(2)和(3)，即可求得故障情况下各端单独作用时的暂态量表达式，简化了计算量。

3 基于故障分解模型的暂态量求解

将图5中的3个电路图与图4进行对比，单端作用的电压和电流的表达式，可以通过将3个图中的参数分别代入公式(2)和(3)进行求解，各端VSC单独作用时的直流电压与直流电流初值为V0、I0，参数如表1。

表1 各端作用时参数具体值

表2 其他参数

由图4可知，3端VSC之间是树状连接，且每端参数一致，同时各端相互之间影响很小，可以忽略，因此各端参数的变化对故障特性的影响相同，以VSC1为例，可以得出：(1)C的变化主要影响与之相连的线路的电流与电压值，在其他因素不变情况下，如果电容值增大，该端电压下降速度将会减慢，电流峰值会增加，但是峰值到来时间会延后。(2)R的变化主要影响电流的峰值，在其他参数保持不变的情况下，增大R，电流峰值会减小，与此同时，电容放电时间有所延长，为保护动作争取时间。(3)如果只增大参数L，该端的电流上升速度和电压下降速度明显减小，可知L具有限流作用，为限流装置的设计提供理论依据。

4 仿真验证

利用MATLAB/SIMULINK工具对树状直流系

统模型进行搭建，通过将仿真结果与计算结果进行对比，来验证结果可靠性。由于直流侧电压的稳定是保证多端直流系统正常运行的基础，因此在受电侧采用定直流电压的控制方式，送电侧采用定有功功率的控制策略，对于3端系统，VSC1与VSC2为送电端，VSC3为受电端[11]。

4.1仿真参数

图6为直流配电系统仿真图，本方法主要突出分解思想，因此为了简化分析过程，所用模型中的线路参数与各端出口电容参数均一致，即假设各端换流站距离相等，故障点设置在中点。VSC1与VSC2采用定电压控制方式，VSC3端采用定功率控制方式，直流侧部分参数如表3[12-13]，仿真时间为2.5 s，故障发生时间在1.5 s。

图6 系统仿真图

4.2仿真验证

对树状直流系统的7个变量暂态表达式的计算结果和仿真结果分别进行了具体对比，为更加清楚地表示故障后的波形，在图7和图8中以故障发生时刻为原点对波形进行绘制。

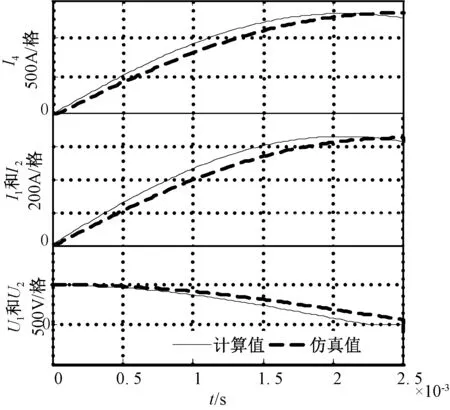
图7 计算结果与仿真结果对比(U1，I1，U2，I2，I4)

为了验证模型的有效性，对以上7个变量的误差进行了分析，由U3曲线可知，该端口的电容放电时间为1.4 ms左右，在0～1.4 ms期间I3的曲线也是接近吻合的。7个变量计算值的平均误差均在10%以下，导致误差的原因有2个方面：一方面是忽略了不同端VSC之间的相互影响；另一方面，在实际过程中，电容放电阶段交流侧的电流会有小部分流入直流系统，计算时未考虑此电流，导致了误差的产生。

图8 计算结果与仿真结果对比(U3，I3)

5 结论

对3端VSC构成的树状直流系统发生极间故障的故障特性进行了分析，在研究过程中，引入分解思想，能够将多端故障模型分解为单端故障模型，得出不同支路电流、不同端电压的暂态表达式，此方法不仅仅局限于3端，具有普遍适用性。根据故障暂态表达式，对线路参数变化所引起的后果进行了详细地分析，为保护值的整定计算和保护方法的研究提供了依据。最后，利用MATLAB/SIMULINK仿真工具验证了结果的可靠性。

[1] 汤广福．基于电压源换流器的高压直流输电技术[M]．北京：中国电力出版社，2010：159-215．

[2] BIFARETTI S，ZANCHETTA P，WATSON A，et al．Advanced power electronic conversion and control system for universal flexible power management[J]．IEEE Transactions on Smart Grid，2011，2(2)：231-243．

[3] 景世良,王毅,许士锦,等. 基于VSC的直流配电网的电压调整控制策略[J]. 电力科学与工程,2016,32(5):7-13.

[4] 胡竞竞，高一波，严玉婷，等．电压源换流器直流侧短路故障特性分析[J]．机电工程，2014，31(4):512-516．

[5] 胡竞竞．直流配电系统故障分析与保护技术研究[D]．杭州：浙江大学，2014．

[6] YANG J，FLETCHER J E，O'REILLY J．Short-circuit and ground fault analyses and location in VSC-based dc network cables[J]．IEEE Transactions on Industrial Electronics，2012，59(10)：3827-3837．

[7] 刘剑，邰能灵，范春菊，等．多端VSC-HVDC直流线路故障限流及限流特性分析[J]．中国电机工程学报，2016，36(19)：5122-5133，5393．

[8] 辛俊峰，韩金铜，康金良. 基于直流电压下降特性的VSC_MTDC控制策略研究[J]. 电力科学与工程，2011，27(8):42-46.

[9] YANG J，JOHN E F，JOHN O，et al．Multiterminal DC wind farm collection grid internal fault analysis and protection design[J]．IEEE Transactions on Power Delivery，2010，25(4):2308-2318.

[10] CHANG B，CWIKOWSKI O，BARNES M，et al．Point-to-point two-level converter system faults analysis[C]//7th IET `International Conference on Power Electronics，Machines and Drives, April Manchester，UK：London: IET，2014：1-6．

[11] 王伟,石新春,付超. 海上VSC-MTDC输电系统协调控制策略[J]. 华北电力大学学报(自然科学版)， 2013,40(5):42-27.

[12] 李斌，何佳伟．柔性直流配电系统故障分析及限流方法[J]．中国电机工程学报，2015，35(12)：3026-3036.

[13] 杨少坤,尹明,刘文丽. 背靠背型柔性直流输电的建模及其控制[J]. 华北电力大学学报(自然科学版)， 2007，34(5):44-47.

A Method Based on Fault Model for Solving Transient Quantity in Tree DC System

XU Yan， LIU Jingyan

(State Key Laboratory of New Energy and Electric Power Systems, North China Electric Power University, Baoding 071003, China)

When a pole-to-pole fault occurs in the multi-terminal VSC system, the fault characteristics are quite complicated. However, the fault characteristic expression of a single-ended VSC system is easy to obtain. Therefore, in this paper, a method of decomposing the fault model according to the number of terminals is proposed. A three-terminal dendritic DC system is taken as an example. The capacitor discharge process of the three-terminal system is decomposed into the processes of three single-terminal capacitance discharge, and the relationship between the single-ended fault model and multi-terminal fault model is analysed. The final results are obtained by solving the transient expression of the single-ended fault model, and the fault characteristics are analyzed. This method greatly simplifies the computational complexity and can be extended to the system with more terminals, so it has a universal applicability. The validity of the method is verified by MATLAB/SIMULINK, which provides the theoretical basis for the fault location research and protection method.

tree DC system；analysis of fault characteristics；decompose fault model；pole-to-pole fault

2017-04-28。

国家重点研发计划(2016YFB0900203)。

10.3969/j.ISSN.1672-0792.2017.08.001

TM731

：A

：1672-0792(2017)08-0001-05

徐 岩(1976-)，男，副教授，博士，主要研究方向为新能源、电力系统继电保护等。

刘婧妍(1993-)，女，硕士研究生，主要研究方向为柔性直流输配电的故障特性及保护技术等。