中国降水回归模型设计策略与回报检验
张凯静,汪萍,戴新刚,程智
(1. 青岛市气象台,山东 青岛 266003; 2. 中国科学院大气物理研究所东亚区域气候环境重点实验室,北京 100029; 3. 中国气象科学研究院大气成分研究所,北京 100080; 4. 93381部队分区气象台,黑龙江 哈尔滨 150223)
中国降水回归模型设计策略与回报检验
张凯静1,2,汪萍3,戴新刚2,程智4
(1. 青岛市气象台,山东 青岛 266003; 2. 中国科学院大气物理研究所东亚区域气候环境重点实验室,北京 100029; 3. 中国气象科学研究院大气成分研究所,北京 100080; 4. 93381部队分区气象台,黑龙江 哈尔滨 150223)
利用中国160站降水记录及欧洲中心ERA-Interim再分析数据等构建了16种线性回归降水预测模型,包括“站点”降水直接/间接预测模型(间接模型是指先预测东亚季风指数,再以此估计站点降水), 以及“区域-站点”降水直接/间接预测模型,即先预测一个区域的降水再分配到站点。此外,还构建了所有模型集合的降水预测模型。预报因子包括两种ENSO指数、北大西洋涛动(NAO)指数和青藏高原积雪深度等4个因子。模型亦分为3因子和4因子(包括积雪因子)组及对降水取/不取对数组等前处理。2005—2016年的回报试验表明,“站点”模型优于“区域-站点”模型,对降水取对数模型优于不取对数模型。另外,“站点”模型组中的间接降水预测模型优于直接模型,但“区域-站点”组却相反。ERA-Interim积雪深度资料不确定性带来的偏差超过该因子对降水预测的贡献。平均PS评分最高的是3因子的直接站点降水取对数模型(MDS-3Ln),平均达到71分,高于集合模型(MEM)得分。这些结果表明,线性回归降水模型的设计理念与实际预测效果可能并不一致,其原因是因子的选取或数学处理过程会引入新的不确定性或偏差,必须综合评估各种设计方案的“成本-效益”关系。
降水预测; 回归方程; 东亚季风; ENSO指数; NAO指数
引言
在气候变暖背景下,中国旱涝灾害频发且呈上升趋势[1]。1991、1998、1999年江淮流域先后出现特大洪涝,造成巨大经济损失和人员伤亡。1999—2001年华北又经历了持续4 a的严重干旱,给农业生产带来严重危害,加剧了水资源危机,致使当地生态环境进一步恶化。因此,每年汛期的旱涝灾害预测十分重要,是一项艰巨的业务任务,做好汛期降水预测对于防灾减灾是关键。目前,短期气候预测主要有三种方法,即概率统计方法、动力学方法以及动力-统计相结合的方法[2-3]。概率统计方法可分为经验数理统计和物理统计方法,二者主要依据过去的观测记录或再分析数据推断未来的天气气候变化。动力学预测方法则依靠大气运动物理原理所设计的数值预报模式,给定初、边值条件,将其放在计算机上积分,给出未来的天气气候预报[4]。这两种预测方法各有优缺点。前者的预测水平主要取决于历史数据的丰度及其平稳性。对于平稳过程,数据的统计性质是收敛的,线性统计模型可以给出可用的预测结果[5]。但实际大气为非平稳过程,数据的统计性质并不收敛,线性统计模型难以得到满意结果[6]。大气数值模式是根据大气运动的物理规律构建,离散化后用于数值模拟实际大气运动过程,从而做出未来的天气气候预测[7]。然而,Lorenz[8]研究发现,大气运动是混沌的,只存在有限的可预报性。由于初始场误差会随着时间增长,因此一般可预报性不超过两周[9]。各种模式的数值试验也都证实了Lorenz的结果,超过两周的天气预报失真严重,参考价值不大。但气候预测毕竟与天气预报在预测目标、预报量、实施方案及用户需求上都有所不同[10]。因此需要建立气候动力学,发展气候预测的动力理论,重新定义气候的可预报性[11-12]。目前,短期气候预测正沿着两个方向发展。第一种是国际上盛行的集合预报方法,即多初值集合预报方法及“多初值+多模式”的超级集合预报方法;第二种是丑纪范院士倡导的动力-统计结合的预测方法[13]。后者利用了动力学方法与概率统计方法之间的互补性,将动力学模式的预报积分数据和大量历史观测数据结合起来,试图减少误差,延长预报时效,以期提高气候预测的水平[14]。中国国家气候中心(NCC)已经建成了动力-统计集成的季节气候预测系统(FODAS)[15-16],在过去8 a的汛期降水预报检验中被证明是一种稳定而有效的预测系统。然而,该系统预报技巧的进一步提高仍然依赖于气候模式的完善、计算机的发展和统计预报方法的进步。值得注意的是,Van Oldenborgh et al.[17]对比欧洲中期天气预报中心的季节预测模式和过去15 a的统计模式预测数据后指出,由于大气运动的准线性特性,简单的、经验的方法仍然具有一定价值。本文以吴志伟等发展的东亚夏季风指数预测模型[18]为基础,构建多种中国夏季降水的统计回归预测模型并进行测试和分析,揭示其中的设计策略并进行评估。
1 数据与方法
1.1 数据
建立回归模型使用的数据有,1979—2016年美国国家海洋与大气管理局(NOAA)气候预测中心(CPC)的Nino3.4指数[19],欧洲中期天气预报中心(ECMWF)再分析资料ERA-Interim中的850 hPa月平均纬向风和积雪深度[20],中国国家气候中心气候诊断预测室的160站月平均降水记录及北京师范大学李建平教授等定义的北大西洋涛动指数(NAOI)等[21]。影响我国汛期降水的因子众多,各因子之间相互关系复杂。中国国家气候中心陈兴芳和赵振国[22]研究指出,影响我国中东部汛期降水的五大主要因子有:东面的海洋、西面的青藏高原、南面的季风、北面的阻塞高压和中间的副高。在太平洋上,厄尔尼诺和南方涛动(ENSO)是影响全球气候年际变化的最强信号,它的发生和发展及衰减都会引起全球气候的变化,对我国的气候,尤其是汛期降水,有明显影响[23-24]。青藏高原积雪可以明显改变高原表面辐射收支、热量及水分平衡等过程,对西太平洋副热带高压强度、位置有明显影响[25]。东亚属于季风气候区,东亚季风指数是预测汛期降水的一个最重要指标,季风偏强年呈南旱北涝型,反之为南涝北旱[26]。北方阻塞形势是影响我国旱涝的另一关键因子。长江流域发生大或特大洪涝的年份几乎都与北方一定的阻塞形势建立和维持关联,其中乌拉尔山阻高是关键因子。万寒和罗德海[27]研究发现,欧亚大陆的阻塞形势类型(pattern)与北大西洋涛动(NAO)的位相有关,正/负位相对应于较少/多的乌拉尔山阻塞高压建立。因此,NAO指数或与此关联的大西洋三极子型海温距平也必然成为预测东亚汛期降水的重要因子之一[28]。
1.2 模型设计
程智[29]曾在吴志伟等设计的东亚夏季风指数预测模型[18]基础上发展了一个全国160站点降水回归预测模型。本文根据程智模型构建了一组预测我国汛期降水的统计回归模型,其预报因子或预报量有东亚季风指数(EAMI)、ENSO指数、北大西洋涛动指数(NAOI)和青藏高原积雪深度等因子。其中EAMI选用中国科学院大气物理研究所张庆云等[30]的定义,它表示东亚两个区域6—8月平均的850 hPa纬向风距平差,其中,区域-1为(10~20°N,100~150°E),区域-2为(25~35°N,100~150°E)。考虑到ENSO发展年和衰减年对中国降水影响的差异,在吴志伟等的模型[18]中,将发展阶段的ENSO海温指数定义为 4—5月平均的Nino3.4指数与2—3月平均的Nino3.4指数之差(ENSOdevelop);在ENSO衰减阶段直接使用12月—次年2月平均的Nino3.4指数(ENSOdecay)作为另一个因子。NAOI有多种定义,本文使用李建平等的定义[21],取其4—5月的平均值。郑益群等[31]分析指出,青藏高原积雪深度的增加,比积雪面积的扩大对夏季气候的影响更大。鉴于此,这里选择再分析数据集ERA-Interim青藏高原区域(28~40°N,80~100°E),1—3月平均积雪深度作为回归因子,记为SNOWdepth。此外,在建立回归模型前,对站点降水序列都做标准化及先取对数再标准化的两种前处理。
考虑到单站降水噪音较大,可以选择先预测一个区域的降水,再按照前期或气候降水分布,估计分配区域内站点的降水。参考我国的九大气候区化[32-33],将全国160站点划分为16个区(图1),各区位置列在表1中。与单站降水的前处理相同,对16个区域降水记录也分别做前处理,即标准化和先取对数再标准化。
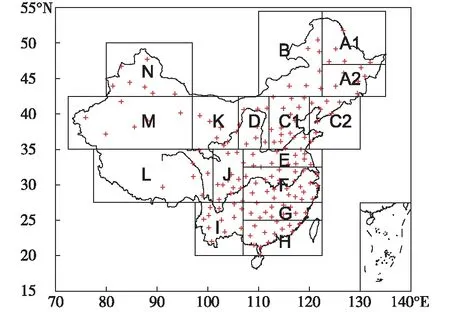
图1 16个区域及代表站点(“+”为代表站点)Fig.1 16 regions and represent stations(“+”)
表116个区域经纬度范围和区内站数
Table 1 The range of 16 regions and the number of represent stations
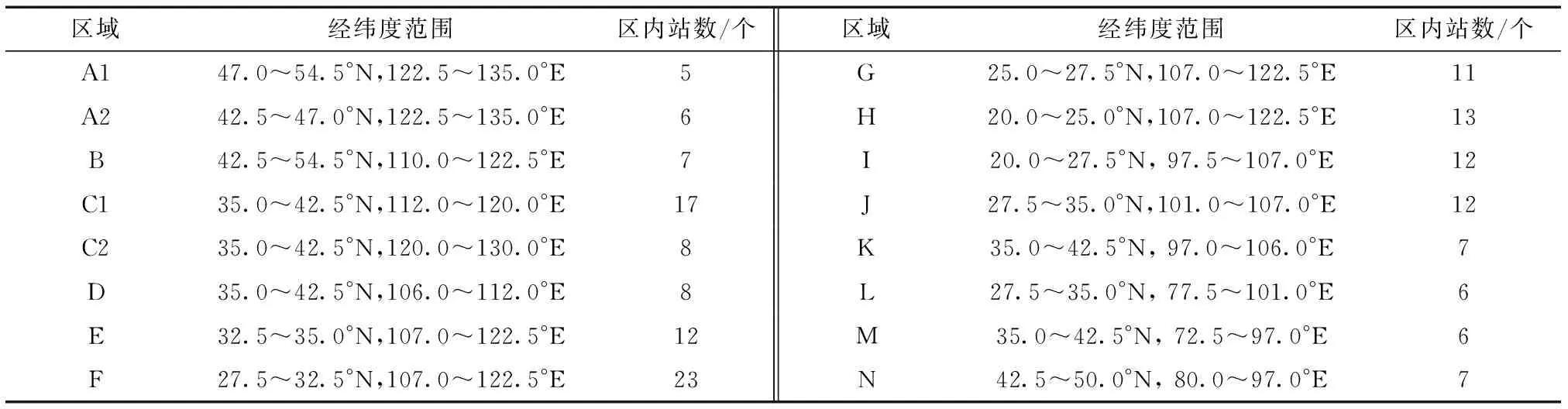
区域经纬度范围区内站数/个区域经纬度范围区内站数/个A147.0~54.5°N,122.5~135.0°E5G25.0~27.5°N,107.0~122.5°E11A242.5~47.0°N,122.5~135.0°E6H20.0~25.0°N,107.0~122.5°E13B42.5~54.5°N,110.0~122.5°E7I20.0~27.5°N,97.5~107.0°E12C135.0~42.5°N,112.0~120.0°E17J27.5~35.0°N,101.0~107.0°E12C235.0~42.5°N,120.0~130.0°E8K35.0~42.5°N,97.0~106.0°E7D35.0~42.5°N,106.0~112.0°E8L27.5~35.0°N,77.5~101.0°E6E32.5~35.0°N,107.0~122.5°E12M35.0~42.5°N,72.5~97.0°E6F27.5~32.5°N,107.0~122.5°E23N42.5~50.0°N,80.0~97.0°E7
1.3 预测模型
吴志伟等的东亚夏季风指数回归模型[18]为:
EAMI=a+bNAOI+cENSOdevelop+dENSOdecay
(1)
东亚季风指数(EAMI)与中国中东部降水异常存在显著的相关关系,为简单起见可以直接依据公式(1)建立EAMI与中国夏季站点/区域降水之间的“回归方程”,即:
Ri=fi+giEAMI(i=1,160)
(2)
公式(1)与(2)联立即是3因子“站点”降水间接预测回归模型(MIS-3),这里“站点”指对160站进行逐站预报。在公式(1)中加入积雪深度因子后就得到4因子的东亚季风指数预测模型:
EAMI=a+bNAOI+cENSOdevelop+
dENSOdecay+eSNOWdepth
(3)
公式(3)与(2)联立即是4因子“站点”降水间接预测回归模型(MIS-4)。另外,还可以写出与此对应的3因子“站点”降水直接预测回归模型(MDS-3):
Ri=ai+biNAOI+ciENSOdevelop+
diENSOdecay(i=1,160)
(4)
及4因子“站点”降水直接预测回归模型(MDS-4):
Ri=ai+biNAOI+ciENSOdevelop+diENSOdecay+
eiSNOWdepth(i=1,160)
(5)
上述回归模型(2)、(4)、(5)中的Ri均为标准化夏季站点降水。由公式(1)和(2)联合或公式(3)和(2)联合构成“站点”降水间接预测模型(MIS-3,MIS-4),即先预测东亚季风指数,再用东亚夏季风指数预测站点降水。由公式(4)或(5)构成的“站点”降水直接预测模型(MDS-3, MDS-4),即利用预测因子直接预测站点降水。若对夏季站点降水先取对数后再做标准化,可以得到对应的4个对数“站点”降水预测模型,简记为MIS-3Ln、MIS-4Ln、MDS-3Ln、MDS-4Ln。若用16个区域降水替换上面8个模型中的站点降水Ri,就得到关于区域降水的8个回归模型。再根据预测/回报年之前7 a平均的区域降水与其内站点降水的分配权重计算出每个站点的降水量作为预测/回报值。“区域-站点”指先预测一个区域的降水再分配到站点。这8个“区域-站点”降水预测模型依此记为:MIA-3、MIA-4、MDA-3、MDA-4、MIA-3Ln、MIA-4Ln、MDA-3Ln、MDA-4Ln。这些模型的预测或回报评估皆用PS评分[34]。
2 降水模型回报检验
2.1 “站点”降水预测模型组
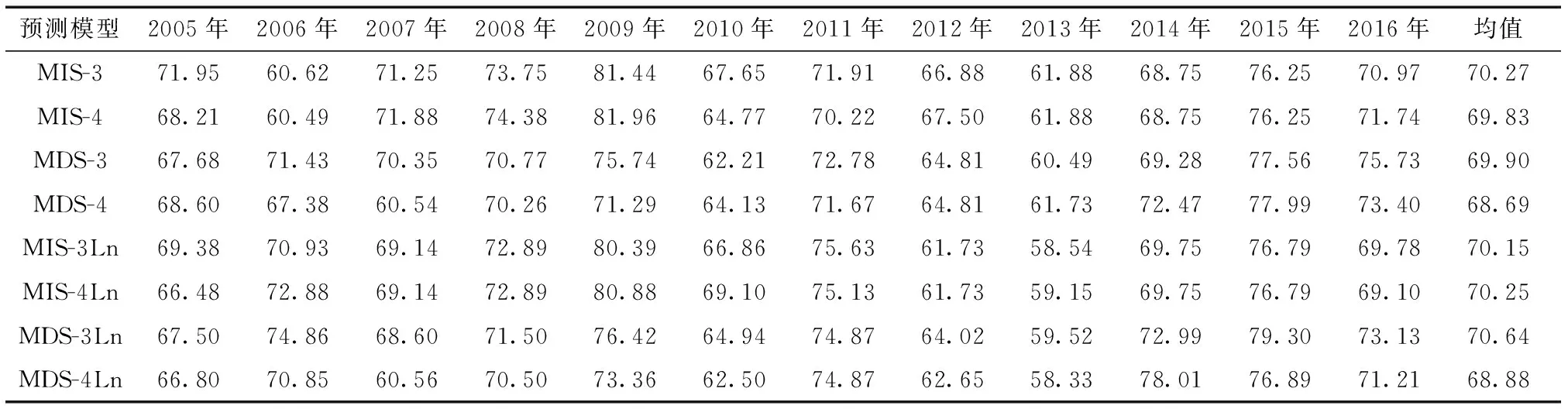
用所设计的上述8个“站点”降水预测回归模型(MIS-3, MIS-4, MDS-3, MDS-4, MIS-3Ln, MIS-4Ln, MDS-3Ln, MDS-4Ln),对2005—2016年逐年夏季站点降水做回报试验,以检验各个模型的预报能力。该组的回报PS评分(表2)显示,除了3因子间接降水预测模型MIS-3外,对降水先取对数再进行标准化前处理的3个模型的评分均高于仅对降水资料做标准化前处理的3个模型,其中前一组有3个模型的平均PS评分大于70。这是因为对数变换使得降水数据线性化,在一定程度上压制了降水序列的非平稳性。此外,比较其中的3因子和4因子预测模型组可知,前一组的PS评分普遍高于后一组,其中只有对数降水模型中的间接降水预测模型(MIS-3Ln, MIS-4Ln)的PS评分相当。这表明ERA-Interim再分析资料的积雪数据可能存在较大的不确定性。分析1979—2010年1—3月JRA-25[35]和ERA-Interim青藏高原积雪深度的逐年变化可知,JRA-25的青藏高原积雪深度呈现显著增加趋势,增加速率为0.3 cm/(10 a),与白淑英等[36]利用遥感资料分析的1979—2010年青藏高原积雪深度增加速率为0.26 cm/(10 a)的变化趋势基本一致,而ERA-Interim的积雪深度呈减少趋势,速率为-0.03 cm/(10 a),因此后者的不确定性较大。许蓓等[37]分析欧亚中高纬地区冬季雪深再分析资料的可靠性时也发现JRA再分析资料与观测事实比较接近。利用JRA-25和ERA-Interim的积雪深度资料,重新构建积雪深度因子序列,带入预测模型组进行计算,在加入JRA-25再分析资料后,4因子预测模型组PS评分普遍较高。由于日本气象厅再分析资料的长度仅截止到2012年,因此本文仍然选择ERA-Interim积雪深度资料作为回归因子。此外,3因子、4因子站点降水预测模型中均是间接降水预测模型组评分较高,说明中国大陆夏季降水异常主要是季风波动造成,只要季风预测准确率高,降水距平的格局就能大致确定, 尽管3因子直接对数降水预测模型(MDS-3Ln)PS评分(70.64)略高于间接模型(MIS-3Ln)。
表2“站点”降水预测模型组回报结果PS评分表
Table 2 PS score of hindcasted precipitation by site-by-site model group
预测模型2005年2006年2007年2008年2009年2010年2011年2012年2013年2014年2015年2016年均值MIS-371.9560.6271.2573.7581.4467.6571.9166.8861.8868.7576.2570.9770.27MIS-468.2160.4971.8874.3881.9664.7770.2267.5061.8868.7576.2571.7469.83MDS-367.6871.4370.3570.7775.7462.2172.7864.8160.4969.2877.5675.7369.90MDS-468.6067.3860.5470.2671.2964.1371.6764.8161.7372.4777.9973.4068.69MIS-3Ln69.3870.9369.1472.8980.3966.8675.6361.7358.5469.7576.7969.7870.15MIS-4Ln66.4872.8869.1472.8980.8869.1075.1361.7359.1569.7576.7969.1070.25MDS-3Ln67.5074.8668.6071.5076.4264.9474.8764.0259.5272.9979.3073.1370.64MDS-4Ln66.8070.8560.5670.5073.3662.5074.8762.6558.3378.0176.8971.2168.88
2.2 “区域-站点”降水预测模型组
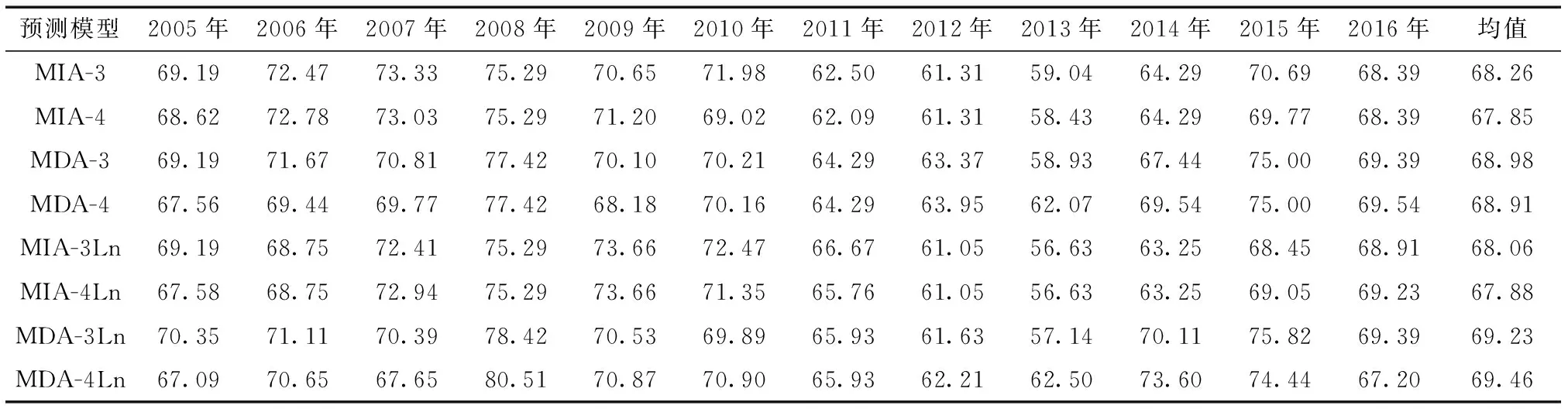
用“区域-站点”降水预测模型组对2005—2016夏季降水进行回报,回报结果(表3)显示,3因子模型的平均PS评分都低于对应“站点”降水预测模型,4因子模型中的2个模型回报PS评分却高于对应“站点”降水预测模型。“区域-站点”的直接对数降水预测模型(MDA-3Ln, MDA-4Ln)的平均PS评分高于对应的标准化降水模型(MDA-3,MDA-4),但间接降水预报模型组(MIA-3,MIA-4,MIA-3Ln,MIA-4Ln)的评分却相差不明显。此结果说明,“区域-站点”的设计可能引入了新的不确定性。尽管区域平均能够压制降水噪音,但从区域到站点降水的分配可能引入了新的偏差,反而导致预测/回报变差,这可能是造成各个模型的回报效果差异较小的原因之一。
表3“区域-站点”降水预测模型组回报结果PS评分表
Table 3 PS scores of hindcasted precipitation by regional-site model group
预测模型2005年2006年2007年2008年2009年2010年2011年2012年2013年2014年2015年2016年均值MIA-369.1972.4773.3375.2970.6571.9862.5061.3159.0464.2970.6968.3968.26MIA-468.6272.7873.0375.2971.2069.0262.0961.3158.4364.2969.7768.3967.85MDA-369.1971.6770.8177.4270.1070.2164.2963.3758.9367.4475.0069.3968.98MDA-467.5669.4469.7777.4268.1870.1664.2963.9562.0769.5475.0069.5468.91MIA-3Ln69.1968.7572.4175.2973.6672.4766.6761.0556.6363.2568.4568.9168.06MIA-4Ln67.5868.7572.9475.2973.6671.3565.7661.0556.6363.2569.0569.2367.88MDA-3Ln70.3571.1170.3978.4270.5369.8965.9361.6357.1470.1175.8269.3969.23MDA-4Ln67.0970.6567.6580.5170.8770.9065.9362.2162.5073.6074.4467.2069.46
2.3 集合降水预测模型组
从表2和表3的回报评分对比中不难看出,“站点”降水预测模型组中3因子直接对数降水模型(MDS-3Ln)的平均PS评分值最高,达到70.64,2015年甚至达到79.30,可将其视为中国夏季降水预测的最优模型。然而,每一模型的逐年回报评分都呈现波动状,其他模型在某个年份的评分也可以很高。例如MIS-4在2009年的评分高达81.96,以及2008年MDA-4Ln模型评分也达80.51。这说明仅用单一模型所做的降水预测存在着很大的不确定性,也许应该构建集合降水预测模型,以减少降水预测的不确定性。一个简单的方式是将16个模型预测值取平均作为降水的集合预测模型,简记为MEM。
表4为2009—2016年最优模型(MDS-3Ln)和集合模型(MEM)的中国夏季降水回报PS评分,以及国家气候中心(NCC)动力-统计预测系统(FODAS)的PS评分。8 a平均PS评分中第一、二、三名分别是FODAS、MDS-3Ln、MEM。但8 a降水回报或预测值的均方差从大到小分别为MEM(41)、MDS-3LN(38)、FODAS(9),可见FODAS的预测方差最小,即模型的稳定性最好。而集合平均模型(MEM)的稳定性还不如站点直接预测模型(MDS-3Ln),与设想相去甚远。因此单一站点模型的回报效果要好于集合平均模型,尽管预计的集合预测模型应该比单一模型回报效果好且稳定。但就个别年份的预报/回报而言,3个模型互有高低。例如,2015、2016年MDS-3Ln和MEM的回报评分都高于FODAS,这是因为后者2009—2016年PS评分大致呈线性下降趋势,而其他模型呈波状起伏。
表42009—2016年最优模型(MDS-3Ln,3因子直接站点降水取对数模型)、集合模型(MEM)及国家气候中心动力-统计短期气候预测系统(FODAS)的PS评分
Table 4 PS scores of the optimal precipitation prediction model (MDS-3Ln,the station direct prediction model with 3 factors and logarithmic precipitation), the ensemble precipitation prediction model(MEM)and the dynamical-statistical integrated forecasting system(NCC/FODAS) from 2009 to 2016

预测模型(系统)2009年2010年2011年2012年2013年2014年2015年2016年均值MDS-3Ln766575646073797371MEM756665625970787569FODAS797275767473727074
3 2015和2016年降水回报
2015年夏季我国降水呈南涝北旱分布,降水偏多地区位于江淮、江南大部、西南东部和北部、新疆、东北东部、内蒙古北部等地;降水偏少地区位于华北大部、内蒙古中西部、新疆南部、黄淮大部、东北西南部、西南南部和西藏等地(图2a)。MDS-3Ln对此的回报也基本正确,回报降水偏多的地区主要位于东北北部、江淮、华东沿海、华南大部、青海、新疆的西部等地;回报降水偏少地区位于华北大部、东北南部、内蒙古中东部、江汉、西南、西北东部、西藏等地(图2b)。该模型的降水符号回报也与实况近似一致。符号正确的站点集中在东北南部、华北、黄淮东部、江淮、江汉、江南中西部、四川东部、西北东部等地;报错符号站点集中在东北北部、内蒙古东部、江南东部、华南大部、西南北部等地(图2c)。
2016年夏季我国降水呈南北两条多雨带分布,长江中下游和华北大部均较常年偏多。具体降水偏多地区位于华北大部、东北南部、西北大部、江汉、江淮西部、江南中西部和华南中部等地;降水偏少地区位于东北北部、内蒙古北部、黄淮东部、江南东部、华南东部和西部、西南、西北和西藏东部等地(图3a)。MDS-3Ln回报的夏季降水近似第二类雨型,即多雨区位于黄河至长江地区,黄河以北和长江以南的大部分地区以少雨为主。具体降水偏多的地区主要为东北中部、黄淮、江淮、江汉、西北和西南的东部、西北西部等地;降水偏少的地区主要为华北大部、内蒙古大部、江南、华南和西南南部等地(图3b)。模型对长江中下游地区降水偏多预测正确,对华北大部降水偏多预测错误。模型回报符号正确的站点集中在东北的北部和南部、西北中西部、黄淮、江淮、江汉、江南东部、华南西部等地;回报符号错误的站点集中在东北中部、华北大部、西北东部、江南中西部、华南中东部、西南等地(图3c)。
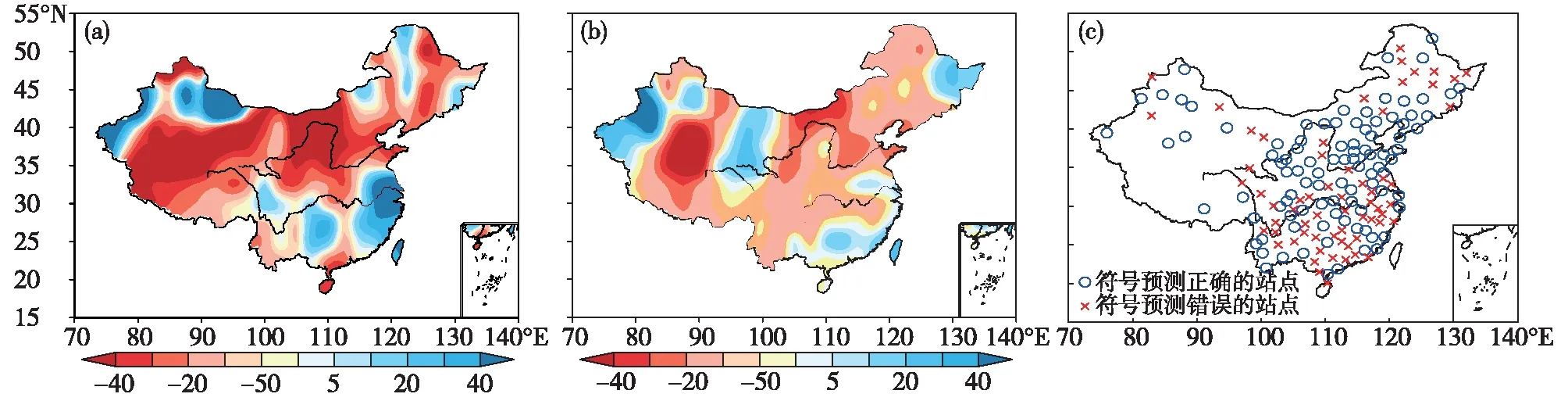
图2 最优模型MDS-3Ln(3因子直接站点降水取对数模型)回报的2015年中国夏季降水(a.实况距平百分率(单位:%),b.回报距平百分率(单位:%),c.距平符号正确站点分布)Fig.2 The hindcasted 2015 summer precipitation by the optimal precipitation prediction model (MDS-3Ln,the station direct prediction model with 3 factors and logarithmic precipitation)(a. observed precipitation anomaly percentage (unit:%) ,b. hindcasted precipitation anomaly percentage(unit:%), c. spatial distribution of the stations correctly hindcasted)
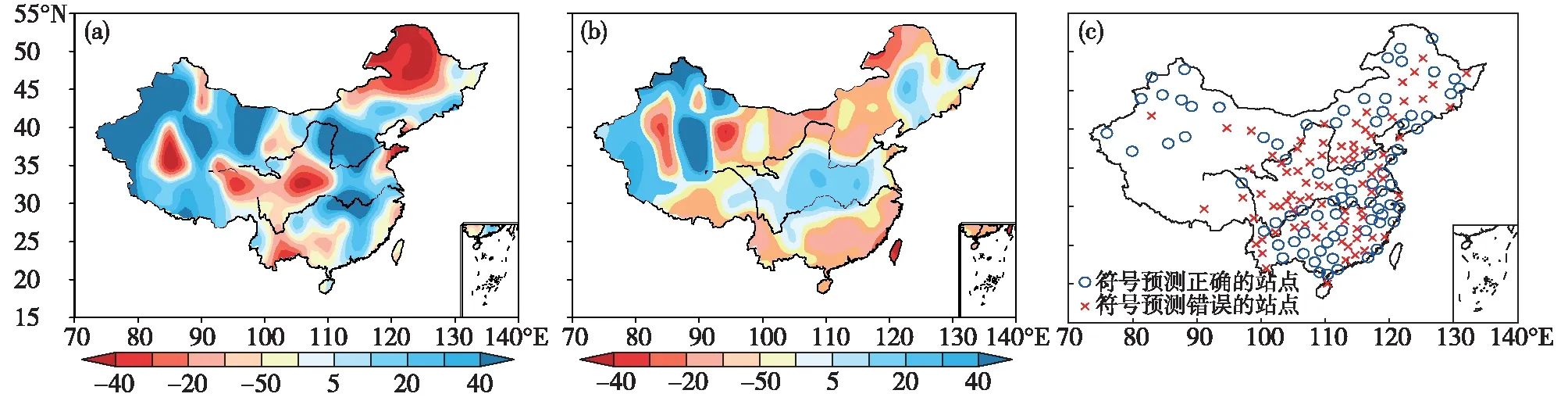
图3 最优模型MDS-3Ln (3因子直接站点降水取对数模型)回报的2016年中国夏季降水(a.实况距平百分率(单位:%),b.回报距平百分率(单位:%),c.距平符号正确站点分布)Fig.3 The hindcasted 2016 summer precipitation by the optimal precipitation prediction model (MDS-3Ln,the station direct prediction model with 3 factors and logarithmic precipitation) (a.observed precipitation anomaly percentage(unit:%), b.hindcasted precipitation anomaly percentage(unit:%), c. spatial distribution of the stations correctly hindcasted)
王东阡等[39]对2015年夏季我国降水异常成因的分析指出,受热带印度洋-太平洋海温异常影响,夏季西太平洋副高偏强、偏南,配合中高纬冷空气活跃,西风急流轴位置偏南,从而造成我国降水南多北少。袁媛等[40]对2016年夏季我国东部降水异常特征分析指出,在El Nio衰减年热带印度洋海温的持续偏暖是导致2016年6—7月副高偏强、偏西的重要外强迫因子。MDS-3Ln对2015年雨带把握较好,对2016年雨带把握有所偏差,这可能与没有考虑印度洋海温异常因子有关。肖子牛和晏红明[41]研究表明, ENSO期间印度洋海温的作用不可忽视,印度洋海温的异常对我国西北、西南,以及长江和黄河下游地区降水的异常变化有重要影响。
4 总结和讨论
本文对16种中国夏季降水统计模型的回报检验表明,绝大多数模型的平均PS评分都超过65分,接近70分,说明因子选取抓住了影响中国夏季降水年际变化的主要因素。尽管设计方案各有不同,在使用ERA-Interim的积雪深度资料作为预测因子时,3因子模型回报效果普遍较好,但如果部分年份使用JRA-25再分析资料重构积雪因子时,4因子模型回报效果普遍较好。研究表明ERA-Interim青藏高原积雪深度资料的质量较低,其不确定性带来的偏差超过了该因子对降水预测的贡献。因此,预报因子的引入也必须做到筛选和评估并重。虽然,降水回归模型的设计理念各有特色,但实际回报检验却肯定了几乎是最简单的逐站对数降水直接预测模型(MDS-3Ln)。结果表明:
1)在一定程度上,过多可靠性较低因子的引入偏差会增加模型不确定性,最优回归模型应该优先考虑可靠性较高的因子。
2)过多的数学处理过程也往往会引入额外的偏差,会增加模型的不确定性。
3)降水序列,特别是站点序列降水的非平稳性较强,需要重视因子的平稳化处理;对降水取对数的线性化处理能提高模型的回报水平。
16种回归模型尚存在较大的改进空间,涉及因子筛选的改进、平稳化数学处理及多模型集合的方法等。必须指出的是,每年中国国家气候中心的汛期预测会商大多安排在3月底或4月初。会上报告的任何统计模型/模式或数值模式所用的观测及再分析数据都无法延伸到春季。因此,本文回归模型中用到的春季海温和NAO指数必须从海-气耦合的数值预测模式或多模式集合预测输出数据中获得。这必然带来新的预测偏差,导致降水预测的PS评分低于回报值。FODAS模式8 a平均的中国夏季降水预测PS评分高达74分,表明动力-统计相结合的策略可能是短期气候预测的优选项之一[42-43]。随着统计方法的改进和数值预报技术的进一步发展,FODAS汛期预测水平可望进一步提高。
[1] 黄荣辉,杜振彩.全球变暖背景下中国旱涝气候灾害的演变特征及趋势[J].自然杂志,2010,32(4):187-195.
[2] 曾庆存.天气预报——由经验到物理数学理论和超级计算机[J].物理,2013,42(5):300-314.
[3] 浦一芬,戴新刚,张仁禾,等.大气科学研究方法[M].北京:科学出版社,2015:333.
[4] 廖洞贤.大气数值模式的设计[M].北京:气象出版社,1999:291.
[5] Wiener N. Extropolation,interpolation,and smoothing of stationary time series[M]. Cambridge:Technology Press, New York:John Wiley and Sons,1947:163.
[6] 洛伦兹 E N .混沌的本质[M]. 刘式达,刘式适,严中伟,译.北京:气象出版社,1997:214.
[7] 曾庆存.数值天气预报的数学物理基础[M]. 北京:科学出版社,1979:543.
[8] Lorenz E N. Deterministic nonperiodic flow[J]. J Atmos Sci,1963,20(2):130-141.
[9] Lorenz E N. A study of the predictability of a 28-variable atmospheric model[J]. Tellus,1965,17:321-333.
[10]丑纪范.天气和气候的可预报性[J]. 气象科技进展,2011,1(2):11-14.
[11]丑纪范,郜吉东.长期数值天气预报[M]. 北京:气象出版社,1995:353.
[12]郭秉荣,江建民,范新岗,等.气候系统的非线性特征及其预测理论[M].北京:气象出版社,1996:254.
[13]丑纪范.为什么要动力-统计相结合?——兼论如何结合[J].高原气象,1986,5(4): 367-372.
[14]戴新刚,浦一芬,汪萍. Lorenz的混沌理论与天气的可预报性[J].气象科技进展,2011,1(2):26-31.
[15]封国林,赵俊虎,支蓉,等. 动力-统计客观定量化汛期降水研究新进展[J].应用气象学报,2013,24(6):656-665.
[16]李维京,郑志海,孙丞虎.近年来我国短期气候预测中动力相似预测方法研究与应用进展[J]. 大气科学,2013,37(2):341-350.
[17] Van Oldenborgh G J,Balmaseda M A,Ferranti L. Did the ECMWF seasonal forecast model outperform statistical ENSO forecast models over the last 15 years? [J]. J Climate,2005,18(16):3240-3249.
[18]Wu Z W,Wang B,Li J P. An empirical seasonal prediction model of the east Asian summer monsoon using ENSO and NAO[J].J Geophys Res,2009,114(D18):85-86.
[19] Trenberth K E. The definition of El Nino[J]. Bull Amer Meteor Soc,1997,78(12):2771-2777.
[20] Dee D P,Uppala S M, Simmons A J,et al. The ERA-Interim reanalysis:configuration and performance of the data assimilation system[J]. Quart J Roy Meteor Soc,2011,137(656):553-597.
[21]Li J P, Wang J X L. A new north Atlantic oscillation index and its variability[J]. Adv Atmos Sci,2003,20(5):661-676.
[22]陈兴芳,赵振国. 中国汛期降水预测研究及应用[M].北京:气象出版社,2000:66-93.
[23]黄荣辉. ENSO及热带海-气相互作用动力学的新进展[J].大气科学,1990,14(2): 234-242.
[24]张人禾,闵庆烨,苏京志.有关副热带太平洋对 ENSO影响研究的综述[J].海洋气象学报,2017,37(1): 1-9.
[25]吴国雄,刘屹民,刘新,等. 青藏高原加热如何影响亚洲夏季的气候格局[J].大气科学,2005,29(1):47-56.
[26]戴新刚,汪萍,张培群,等.华北降水频谱变化及其可能机制分析[J].自然科学进展,2003,13(11):1182-1189.
[27]万寒,罗德海. 北半球冬季阻塞环流与NAO之间的关系[J].热带气象学报,2009, 25(5):615-620.
[28]左金清,李维京,任宏利,等.春季北大西洋涛动与东亚夏季风年际关系的转变及其可能成因分析[J].地球物理学报,2012,55(2):384-395.
[29]程智. 一种预测我国汛期降水统计模型的建立[J].安徽农业科学,2011,39(16): 9877-9878.
[30]张庆云,陶诗言,陈烈庭.东亚夏季风指数的年际变化与东亚大气环流[J].气象学报,2003,61(4):559-568.
[31]郑益群,钱永甫,苗曼倩.青藏高原积雪对中国夏季风气候的影响[J].大气科学,2000,24(6):761-774.
[32]苗娟,林振山.我国九大气候区降水特性及其物理成因的研究I——基本特性分析[J].热带气象学报,2003,19(4):377-388.
[33]苗娟,林振山.我国九大气候区降水特性及其物理成因的研究II——我国各区降水与环流因子的关系[J].热带气象学报,2004,20(1):64-72.
[34]陈桂英,赵振国.短期气候预测评估方法和业务初估[J].应用气象学报,1998,9(2):178-185.
[35] Onogi K, Tsutsui J, Koide H, et al. The JRA-25 reanalysis[J]. J Meteor Res Japan, 2007, 85(3): 369-432.
[36]白淑英,史建桥,高吉喜.1979-2010年青藏高原积雪深度时空变化遥感分析[J].地球信息科学,2014,16(4):628-637.
[37]许蓓,陈海山,高楚杰. 冬季雪深再分析资料在欧亚中高纬地区的适用性评价[J]. 气候与环境研究,2015,20(3):296-306.
[38]肖莺,任永建,杜良敏.2015/2016年海洋和大气环流异常对中国夏季降水的影响[J].自然资源学报,2016,31(12):1995-2004.
[39]王东阡,王艳娇,崔童.2015年夏季气候异常特征及其成因简析[J].气象,2016,42(1):115-121.
[40]袁媛,高辉,柳艳菊.2016年夏季我国东部降水异常特征及成因简析 [J].气象,2017,43(1):115-121.
[41]肖子牛,晏红明. El Nio位期间印度洋海温异常对中国南部初夏降水及初夏亚洲季风影响的数值模拟研究[J].大气科学,2011,25(2):173-183.
[42]范可,田宝强,刘颖.2015/2016年极强厄尔尼诺事件下我国动力和统计相结合实时气候预测研究[J].大气科学学报,2016,39(6):744-755.
[43]封国林,赵俊虎,杨杰. 中国汛期降水动力-统计预测研究[M]. 北京:气象出版社,2015:329.
ThedesignstrategyandhindcastingexperimentofChinaprecipitationusingregressionmodel
ZHANG Kaijing1,2, WANG Ping3, DAI Xingang2, CHENG Zhi4
(1.QingdaoMeteorologicalObservatory,Qingdao266003,China; 2.KeyLaboratoryofRegionalClimate-EnvironmentforTemperateEastAsia,InstituteofAtmosphericPhysics,ChineseAcademyofSciences,Beijing100029,China; 3.InstituteofAtmosphericComposition,ChineseAcademyofMeteorologicalSciences,Beijing100080,China; 4. 93381ArmySubregionMeteorologicalObservatory,Harbin150223,China)
16 kinds of linear regression prediction models are developed based on precipitation data of 160 stations in China and ECMWF reanalysis data (ERA-Interim). The models include station direct/indirect precipitation prediction model group (in indirect models, the East Asian monsoon index is firstly predicted, and based on which, station precipitations are predicted.), region-station direct/indirect precipitation prediction model group (regional precipitations are firstly predicted, and then distributed to the stations). In addition, an ensemble precipitation prediction model is composed with those 16 models as members. There are totally 4 factors in the regression equations, including two types of ENSO index, North Atlantic Oscillation(NAO)index and the mean snow depth on Tibetan plateau.According to the number of factors, the models can also be grouped into 3 factors (including the ENSO indices and NAO index) models or 4 factors (contains all the factors) models. In addition, the differences of the models also lies in their predictor, precipitation or its logarithm. Hindcast for 2005—2016 shows that the average PS score for the station prediction model group is higher than that of region-station prediction model group. The performance of the models taking logarithmic precipitation as predictor is better than those using precipitation itself as predictor. In the station prediction model group, the indirect precipitation prediction models are usually superior to the direct ones, while it is opposite for the region-station model group. For precipitation prediction, the deviation caused by the uncertainty in snow depth of ERA-Interim reanalysis data is greater than the contribution of the factor of snow depth. Among all the models, the direct station prediction model with 3 factors for logarithmic precipitation (MDS-3Ln) get the highest PS score on average, reaching 71 point, which is higher than that of the ensemble model (MEM). It is indicated that the real performance of a linear regression precipitation model is not always consistent with its design strategy, since new factors or processing methods may induce new uncertainties or deviations. Therefore, it is necessary to evaluate the Cost-Effectiveness in model development.
precipitation prediction; regression equation; East Asian monsoon; ENSO index; NAO index
10.19513/j.cnki.issn2096-3599.2017.03.004. (in Chinese)
2017-05-30;
:2017-07-13
国家自然科学基金项目 (41475075,41075058);国家重点研发计划项目(2016YFA0601901);青岛市气象局科研项目(2015qdqxh02)
张凯静(1985—),女,硕士,工程师,主要从事气候变化及气候预测研究,qdsky2007@126.com。
戴新刚(1958—),男,博士,研究员,主要从事气候动力学与气候预测研究,daixg@mail.iap.ac.cn。
P46
: A
: 2096-3599(2017)03-0027-09
10.19513/j.cnki.issn2096-3599.2017.03.004
张凯静,汪萍,戴新刚,等.中国降水回归模型设计策略与回报检验[J].海洋气象学报,2017,37(3):27-35.
Zhang Kaijing,Wang Ping,Dai Xingang, et al. The design strategy and hindcasting experiment of China precipitation using regression model [J]. Journal of Marine Meteorology, 2017,37(3):27-35.

