实现AES加密算法代数表现形式的研究

彭关礼，周 琴

（西华师范大学，四川 南充 637009）

实现AES加密算法代数表现形式的研究

彭关礼，周 琴＊

（西华师范大学，四川 南充 637009）

针对AES加密算法中相对代数描述较弱的缺点，文章提出一种用代数多项式的表示方法来实现对该加密算法的整体描述，主要通过构建部分变换模块的多项式将其结合起来形成多项式环，从而构建整个AES加密算法的代数多项式。

AES加密算法；代数多项式；多项式环

高级加密标准（Advanced Encryption Standard，AES）因具有对称性、模块性、高效性等特点而被全世界所广泛采纳。目前虽然没有实际的例子证明AES算法安全性遭受到威胁，但大多数研究人员从数学理论的角度出发对AES加密算法进行了分析与研究，试图利用代数方法进行攻击破解。文献[1]提出了一种代数计算攻击（XSL攻击）。对于这些攻击方法是否有效仍然是未知的，但至少给研究者提供一种分析的方法。然而许多研究者在利用代数方法进行描述时仅对该算法的部分采用了代数的形式表示没有能对其整个算法进行代数描述，文献[2]基于AES加密算法部分代数描述不利于对该算法的分析与研究，本文提出一种运用代数多项式来实现AES加密算法的整体代数描述。

1 AES加密算法的分析

AES采用对称分组加密模式其明文分组大小为固定值128 bit，32 bit为一个字，则以字为单位的明文分组长度Nb=4；而密钥分组的不同决定加密的轮数，用Nk表示密钥分组长度，Nr表示对应的加密轮数，对于分组大小128 bit的密钥其Nk=4，Nr=10；对于分组大小为192 bit的密钥其Nk=6，Nr=12；对于分组大小为256 bit的密钥其Nk=8，Nr=14。

AES加密算法主要分为轮变换和密钥扩展两部分，而解密过程是加密过程的逆变换操作。轮变换过程中除最后一轮省略了列混淆（MixColumns）外，每轮的轮变换操作都具有相同字节代换（SubBytes）、行位移变（ShiftRows）、列混淆（MixColumns）、轮密钥加（AddRoundKey）等4个主要步骤。而轮密钥加（AddRoundKey）操作又可以作为一个单独的步骤，其是将经过变换后的数据抽象的看作状态与密钥扩展算法所获得的轮密钥进行相应的异或操作。

2 如何构建AES的代数表示形式

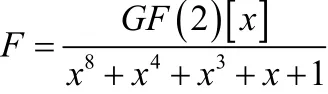
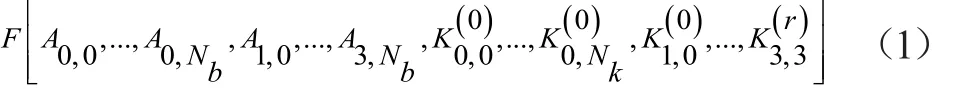
3 轮函数的代数表示

3.1 字节替代

设m是定义在F上的可逆变换函数且b∈为对应的仿射变换函数。构建可逆变换函数m的多项式m（A）i,j=（Ai,j）254，每个元素映射成该元素的逆，多项式b∈F为仿射变换。对函数的差分传播和相关特性研究，用拉格朗日插值定理和迹函数实现。设F={x0…x255}并且V:F→则：

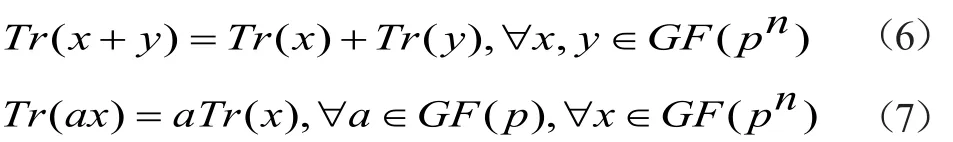
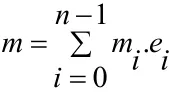
设W表示8×8的矩阵用于表示仿射变换，同时设b'=W·m，m∈GF（28）则：

3.2 行位移变换

AES算法将128 bit数据分成4行4列，正向或逆向行位移变换的过程中，每行字向左或向右循环偏移相应的字节，分组长度与对应位移偏移量的关系如表1所示。可以用式（15）式和式（16）的代数形式表示加密和解密的行位移变换。

表1 分组长度对应的位移偏移量

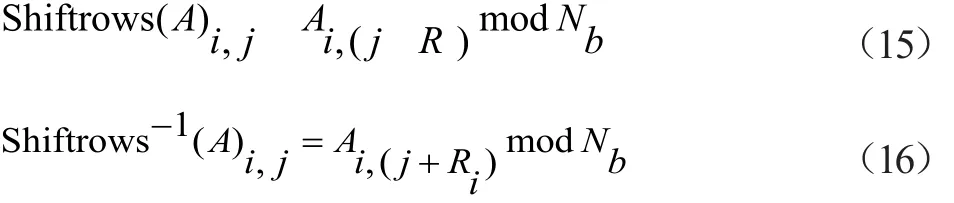
3.3 列混淆

AES加密算法列混淆在本质上已经属于代数形式。为形象地描述列混淆实现的过程，将式（17）列混淆的矩阵表示替换为式（18）的代数表示。

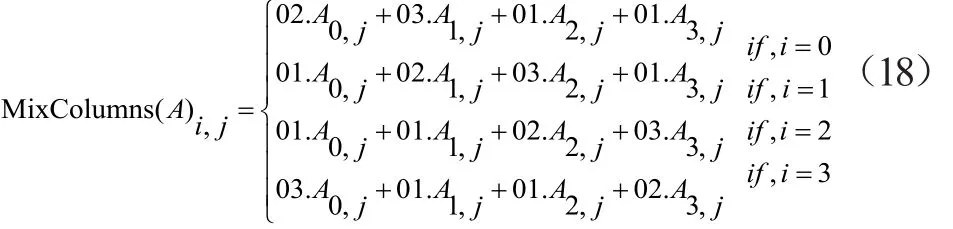
3.4 轮密钥加

轮密钥加在所有轮函数中具有最简单的代数形式，该操作由128 bit的明文经过字节代换，行位移变换，列混淆（除最后一轮外）后与每轮密钥进行简单的异或相加。轮密钥加的代数形式可以表示为：

4 AES加密算法的代数表示

轮函数中各部分之间的关系构建AES加密算法的整体代数多项式。设f表示轮函数（除轮密钥加）中的每一步或整个轮函数的组成g表示加密函数的部分或整体，任意输入变量A用一个多项式方程g(f(A))i,j来表示部分加密或整体加密，其中0≤i≤3，0≤j≤Nb。

计算方法：

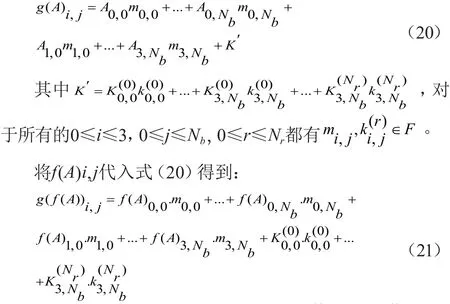
轮密钥用常量函数表示而不能用f(K(r))i,j替换K(r)i,j，能很快实现AES加密算法的代数表示。

5 结语

AES加密算法进行代数多项式表示，并非实现其严格意义上的代数表示，需要构建多项式适合于函数f，函数g满足多项式g(A)i,j，这样才能够满足g(f(A))i,j的运算。因此构建AES加密算法的代数表现形式是为研究人员提供一种方法来实现对该算法的深入研究与分析，可以利用这种方法找到一种更适合研究者需要代数表示方法。

[1]段绍华.高级数据加密标准的代数攻击方法研究[D].长沙：中南大学，2008.

[2]马虹博，刘连浩.AES的S盒和逆S盒的代数表示[J].计算机工程，2006（18）：149-151.

[3]丘维声.高等代数下册—大学高等代数课程创新教材[D].北京：清华大学出版社，2010.

[4]刘绍学，郭晋云.环与代数[M].北京：科学出版社，2009.

Study on algebraic representation of AES encryption algorithm

Peng Guanli, Zhou Qin*
（China West Normal University, Nanchong 637009, China）

Aiming at the weakness of relative algebra in AES encryption algorithm, this paper proposes a representation method of algebraic polynomial to realize the overall description of the encryption algorithm, which is formed polynomial ring by combining polynomial of partial transformation modules to construct the algebraic polynomial of the entire AES encryption algorithm.

AES encryption algorithm; algebraic polynomial; polynomial ring

彭关礼（1988— ），男，四川万源人，硕士；研究方向：无线电物理。

＊通信作者：周琴（1988— ），女，四川武胜人，硕士，助教；研究方向：偏微分方程数值解。