大面积露天采矿方量计算方法探讨
郭正一++杜永红++韩健++任俊儒
【摘 要】精确算量在露天矿日常生产过程中尤为重要。通过对国内外算量的方法进行研究,建立了改进的方格网法、改进的三角网法及两者有机结合的模型,并且用C#和MATLAB混合编程来实现算法。采用联合CASS算量和实地过磅进行对比分析,此方法在满足条件下可以在允许存在误差范围内合理得出方量,可以在以后计算机算量方面建立选择算量方法做一些改进,以确保算量的精确、合理。
【Abstract】The exact calculation is very important in the daily production of open pit. Through the research on the method of calculating the amount in and out, an improved square grid method, improved triangulation method and organic combination model are established, and the algorithm is implemented by C # and MATLAB mixed programming. We can use the CASS to calculate the amount of the field scale. This method can reasonably obtain the square quantity in the range of the allowable error, and we can make some improvements in the calculation of the amount of computer calculation and make the amount of accurate and reasonable.
【关键词】大面积;露天采矿;不规则算量
【Keywords】large-scale; open-pit mining; irregular calculation
【中图分类号】TD172 【文献标志码】A 【文章编号】1673-1069(2017)08-0184-03
1 引言
矿山开采过程中,精确算量成为联系甲方和乙方的重要工作。客观地从甲方和乙方的利益角度着想,甲方与乙方均期望测量出来的方量是精确的,不容虚假[1]。算量理论和算量方法也影响着结果。本文采用改进断面法和改进三角网法,以及两种方法针对不同表面条件下合理结合应用,通过实际对比和实验分析,发现此方法具有很好的精确性。
算量的方法大致是通过断面法、方格网法、三角网法进行算量,此外,遗传算法在有些国家也应用到算量方法中。国内主要根据以上方法进行算量,以及在其基础上加以约束和修正条件,获得更精确的方量。
2 理论基础
2.1 改进方格网法
传统方格网法是将所需算量的区域分割成大小一样的方格,然后依据高差值来计算每个立方体的体积,再求和即获得此区域的总量。具体公式如下:
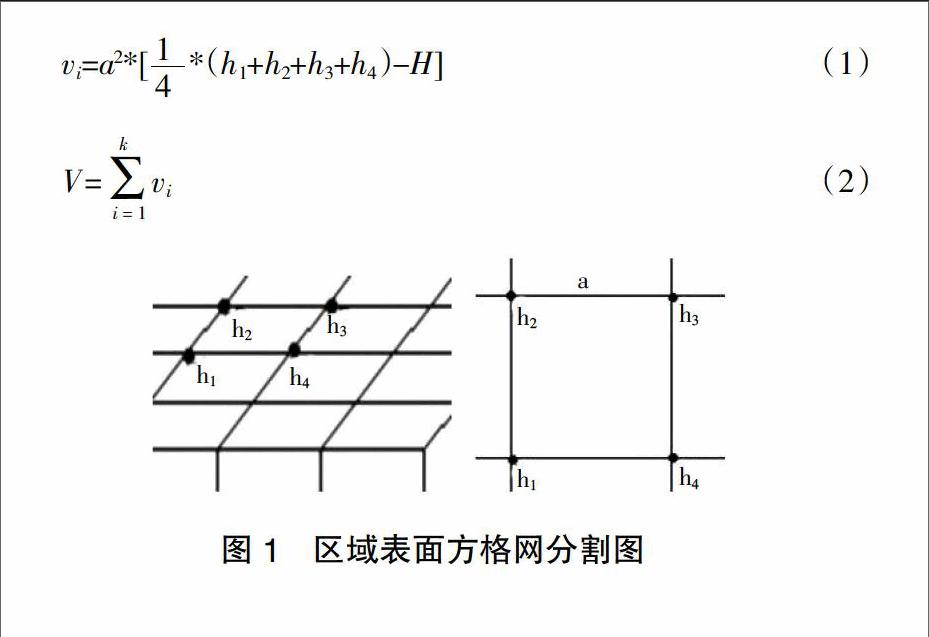
vi=a2*[■*(h1+h2+h3+h4)-H] (1)
V=■vi (2)
■
图1 区域表面方格网分割图
其中a为方格网边长,h1、h2、h3、h4分别为对应点的高程,H为基准高程。
改进的方格网法是将表面按曲面拟合,将每一个小方格按一个二次函数进行表面拟合,然后再求重积分,解算出每个曲顶立方体的体积,再进行求和,即可求出此区域总量。具体算法如下:根据四角点坐标可以确定二次及以上曲面函数:
f(x,y,z)=axn+byn+czn+d (3)
本实验,取n=2。
然后,对其竖直投影面积内进行积分,有如下公式:
■ (4)
然后,带入公式(2)得出此区域精确的量。
传统方格网法对地面的平整度要求高,当地面起伏较大或高程变化很大时,就不适用。计算精度与场平面积、边长、等高距、坡度及施工高度等因素有关。经过改进的方格网拓宽了要求,但是,方格网边长依然直接影响精度。通过实验数据对比发现:改进方格网法比传统方格网法精度上有提高[2]。
2.2 改进三角网法
三角网法是把离散的地形特征点以一定的规则构造出邻接的三角网,其中最常用的是TIN法。TIN是DTM表现形式之一,尤其是在有约束条件下建模生成三维模型[3]。不规则三角网的算量模型如下:
Vi=s*Hi (5)
■
(a) (b)
图2 区域表面三角网模型计算图
结合公式(2)可得出总量。其中Vi表示某三棱柱体的体积,s表示相应的三角形投影面积,表示相应A到a的高差。
但是部分情况下,TIN法不一定能很好地算出区域的方量,例如大规模自然形成的表面,且不平整,利用不规则三角网算量导致整体舍入误差增大。将三角网表面进行修正然后经过重积分就可以求出更为精确的方量,计算方法如下:先经过三个点进行插二次曲面,函数如下:
f(x,y,z)=ax2+by2+cz2+d(6)
要求(6)中的一阶偏导数在随机点的值是相等的,附加边界点的约束条件即可求出每个小的曲面的曲面方程,实现算法时,采用边界约束条件是:边界点的一阶偏导数为零。然后在其投影面上做重积分,就可以求出方量,公式如下:
■ (7)
结合公式(2)可得方量。经改进后,结合MATLAB和C#混合编程实现改进后的算法,算出自然形態下的方量比改进前的更合理。endprint

