考虑随机变量相关性的桥梁地震易损性分析*

李立峰，李辉辉，徐开铎，胡思聪

(湖南大学 土木工程学院，湖南 长沙 410082)

考虑随机变量相关性的桥梁地震易损性分析*

李立峰†，李辉辉，徐开铎，胡思聪

(湖南大学 土木工程学院，湖南 长沙 410082)

引入Nataf变换，结合均匀设计响应面法，提出了一种综合考虑地震动和结构不确定性及结构参数相关性的桥梁地震易损性分析方法.以一多跨连续梁桥为研究对象，分别对算例桥梁在考虑与不考虑结构参数相关性情况下进行了地震易损性分析.同时，分析了考虑结构参数变量相关性对结构易损性分析和响应面模型精度的影响.结果表明：本文方法可以有效考虑结构参数之间的相关性，且考虑变量相关性后建立的响应面能够更好地拟合结构真实的极限状态函数曲面;桥梁结构在各个破坏状态下的失效概率均有一定程度的降低;忽略结构参数相关性的影响，可能会低估桥梁结构在地震作用下的抗震性能.

桥梁地震易损性；随机参数；相关性；Nataf变换；均匀设计响应面法

地震易损性可以反映桥梁结构在不同强度地震动作用下，其地震需求能力超过指定损伤状态的条件概率.桥梁结构地震易损性受多种不确定性因素影响，而这些不确定性主要来源于地震动和结构等方面，国内外学者对此作了大量研究.Casciati等[1]将结构性能阈值定义为随机变量来考虑结构不确定性，对斜拉桥进行了地震易损性分析；Banerjee等[2]采用能力谱分析方法(CSM)对美国加州地区的桥梁进行易损性分析时，将桥墩地震响应转化为反应谱分析来考虑结构抗震能力的不确定性，并建立和对比了该方法与传统非线性时程分析所得到的地震易损性曲线；Hwang[3]等在研究一座四跨连续梁桥的地震易损性时，采用拉丁超立方抽样(LHS)方法考虑了地震波、土壤力学、钢筋屈服强度等参数以及边界条件等多种不确定性因素的影响；李立峰等[4-5]在研究中等跨径RC连续梁桥和板式橡胶支座地震易损性时，考虑了地震动和结构主要材料参数的不确定性；庞于涛等[6]、沈国煜等[7]在对斜拉桥和连续梁桥进行地震易损性分析时，考虑了地震动、钢筋和混凝土本构及结构几何参数等不确定性；唐和生等[8]在对一钢框架进行抗震稳健性优化设计时，基于Info-Gap理论模型来描述地震设计谱中反映地面运动强度的水平影响系数最大值αmax和场地特征周期Tg，研究了结构抗震设计中存在的不确定性问题.

目前，关于地震动不确定性的分析已相对成熟，而对于结构的不确定性，主要是通过将影响结构不确定性的各个参数(材料参数、结构几何参数)视为随机变量的方式来考虑.在以往的相关地震易损性分析中,为了分析简便,一般假设各随机变量相互独立，而考虑变量之间相关性对结构地震易损性分析影响的研究较少.然而,在实际工程情况下,忽略结构参数等随机变量相关性的影响可能会高估桥梁结构在特定强度地震动作用下的易损程度.为此，有必要对地震动、结构参数等随机变量间的相关性对桥梁结构地震易损性分析的影响进行研究.

对于随机变量相关性的处理，国内外学者进行了一些研究.Liu等[9]在研究结构可靠度问题时，首次提出了Nataf变换后的等效相关系数的经验计算公式，研究了Nataf变换在处理随机变量相关性问题时的适用性；吴帅兵等[10]建议在处理相关非正态变量的结构可靠度计算问题时，应该考虑映射变换时相关性的变化，宜优先采用Nataf变换；吴帅兵等[11]比较了Orthogonal变换、Rosenblatt变换和Nataf变换的优缺点、适用范围及其对结构可靠度的影响，验证了Nataf变换在用于结构可靠度分析时具有计算精度高和适用范围广的优点，建议在处理变量相关变换时优先采用.以上研究结论均表明，忽略随机变量相关性，会对结构可靠度分析产生很大影响，同时Nataf变换是一种高效、合理解决随机变量相关性问题的方法.

因考虑随机变量相关性的桥梁地震易损性研究较少，本文通过引入Nataf变换，结合均匀设计响应面法，提出了一种综合考虑地震动和结构不确定性、考虑随机变量相关性的桥梁地震易损性分析方法.以一多跨连续梁桥为研究对象，通过Nataf变换处理包括核心混凝土、保护层混凝土、纵向钢筋及桥墩直径等参数在内的11个相关的结构参数随机变量，采用均匀设计构造结构-地震动样本对，并以桥梁支座位移、墩柱曲率为结构响应，建立桥梁结构响应与结构及地震动参数之间的响应面模型，对算例桥梁进行了易损性分析.同时，本文在考虑结构参数随机变量相关性后对结构易损性分析和响应面模型精度的影响进行了分析，并得出相应结论.

1 考虑随机变量相关性的地震易损性分析方法

1.1 Nataf变换基本原理

Nataf变换是根据一组相关随机变量的联合累积分布函数、相关系数矩阵，结合Nataf分布和基于特征值分解的线性变换[12]，其基本原理为：

若已知一组相关非正态分布随机变量组X=(X1，X2,…，Xn)T，其联合累积分布函数为Fx(x)，相关系数矩阵ρ=(ρij)n×n，X的第i个随机变量Xi的边缘累积分布函数为FXi(Xi)，根据等概率变换原则有：

Φ(Yi)=FXi(Xi).

(1)

式中：Yi为标准正态分布随机变量.变量Xi和Yi存在以下关系：

(2)

式中：Φ-1(·)和FXi-1(·)分别为标准正态分布累积分布函数和Xi边缘累积分布函数的反函数.根据式(2)可将变量X变换为一组相关的标准正态分布变量Y，并且其联合概率密度函数存在以下关系：

(3)

式中：φn(y,ρ0)为相关系数矩阵；ρ0=(ρ0ij)n×n为变量Y的联合概率密度函数.一般地，文献[9]将式(3)构造的随机变量X的概率分布模型称为Nataf分布[10].根据相关系数的定义，由式(2)和式(3)可得变量X的相关系数ρij与其等效标准正态变量Y的相关系数ρ0ij有以下关系：

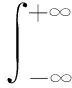
φ2(yi,yj,ρ0ij)dyidyj.

(4)

式中：φ2(yi,yj,ρ0ij)为相关系数为ρ0ij的二维标准正态分布联合概率密度函数.当变量Xi和Xj的边缘分布函数及相关系数ρij已知时，可通过求解式(4)所示非线性方程组来确定其等效相关系数ρ0ij.然而，在求解式(4)所示非线性方程组时，其求解过程非常复杂，并且当ρij接近于1或-1时，ρ0ij可能无解.为避免求解上述非线性方程组，Liu等[9]通过最小二乘法给出了10种常见边缘分布的经验计算公式，如式(5)所示：

ρ0ij=Fρij.

(5)

式中：系数F≥1，与变量的分布类型、相关系数和变异系数有关.变量Y的相关系数矩阵ρ0=(ρ0ij)n×n是一对称正定矩阵，可对其进行柯西分解(Cholesky分解)得下三角矩阵L，左乘L的逆矩阵L-1可将相关标准正态变量Y转化为独立的标准正态变量Z，此过程也被称为正交变换.

Z=L-1Y.

(6)

基于上述Nataf变换原理，可将一组相关随机变量组X变换为独立标准正态分布变量组Z，从而可对Z进行试验设计来构造试验样本.

1.2 均匀设计响应面法

响应面方法，通过一组经试验设计样本点回归拟合得到响应与设计变量之间复杂的隐式函数关系，是一种试验设计与数理统计相结合的方法[13].常采用的含交叉项的二次多项式响应面如式(7).

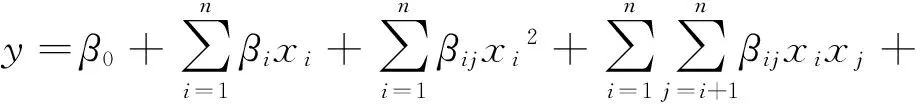
(7)

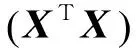
(8)

式中：β为待定系数矩阵，且

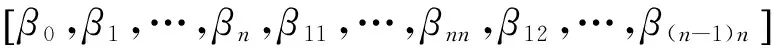
X为样本点矩阵，

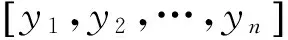
根据文献[14]，评价式(7)所建立的响应面模型精度，可通过测定拟合系数R2和修正拟合系数Ra2与1的逼近程度来检验(与1越接近表示响应面模型精度越高，所构造的响应面能更好地拟合真实极限状态函数)，其中R2和Ra2的表达式如下：

R2=SSR/SST,

(9)

Ra2=1-(1-R2)·(n-1)/(n-m).

(10)

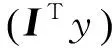
由均匀设计理论[13]，根据设计变量数和均匀设计表偏差,选择合理的均匀设计表来构造试验样本,从而建立结构响应与设计变量间的响应面模型.

1.3 考虑随机变量相关性的地震易损性分析流程

根据Nataf变换、均匀设计响应面法的基本原理，考虑随机变量相关性的地震易损性分析主要流程为：

1)确定影响结构不确定性的结构参数随机变量X，其边缘分布及相关系数矩阵ρ.

2)根据等概率变换原则将变量X转化为与其等效相关的标准正态分布变量Y，并由Nataf变换确定变量Y的相关系数矩阵ρ0.

3)根据正交变换，将变量Y转化为独立的标准正态分布变量Z.至此，完成了前处理工作，即将一组相关的结构参数随机变量X变换为独立正态分布变量Z，并把变量Z作为结构参数输入.

4)选取合理的响应面函数，确定桥梁结构响应与各设计变量.

5)依据桥梁场地条件选取地震波，将地面峰值加速度PGA作为地震动参数输入，通过均匀设计建立“结构-地震动”样本对，并进行相应次数的全过程非线性时程分析，提取结构响应值.

6)进行响应面函数拟合，对响应面模型进行精度检验.若精度符合要求，则进行下一步，否则返回步骤5)重新构造样本对.

7)定义结构损伤指标，计算桥梁结构在相应损伤状态的失效概率，并建立地震易损性曲线.

2 桥梁算例

2.1 桥梁概况及有限元建模

算例为一跨径布置为5×30 m的钢筋混凝土连续梁桥，其主梁为C50混凝土箱梁，梁高1.8m；盖梁采用C40混凝土；桥墩为直径1.4m的钢筋混凝土圆形墩，采用C30混凝土，墩高8m，纵筋和箍筋均采用HRB335钢筋，纵筋配筋率为1.08%，体积配箍率为0.58%，纵筋直径为28mm，箍筋直径为10mm，混凝土保护层厚度为8cm；桥梁支座采用板式橡胶支座.

本文采用OpenSees程序[15]建立桥梁非线性动力有限元模型，如图1所示.桥梁上部结构采用弹性梁柱单元模拟,桥梁墩柱采用弹塑性纤维单元模拟.在桥墩弹塑性纤维单元中，核心混凝土与保护层混凝土采用Mander模型，且不考虑混凝土抗拉性能；钢筋采用双直线模型.桥台采用Aviram等[16]提出的简化弹簧系统,其接触单元仅由一个连接弹簧组成,即不考虑碰撞过程中能量的损失，并假定桥台不发生变形.接触单元的非线性力-位移关系为：

(11)

式中：d0为桥台与主梁间的初始间隙(即伸缩缝大小)；y为地震作用下主梁与桥台的相对位移；KP为接触碰撞刚度.对于KP的取值，由于缺乏试验依据，在以往的研究中通常假定弹簧刚度很大，本文参考主梁的轴向刚度，KP取值为3.02×106kN/m.承台底部固结，不考虑桩-土间的相互作用，场地条件为Ⅱ类，地震波仅考虑纵桥向输入.

图1 桥梁有限元模型图Fig.1 Finite element model of bridge

2.2 结构响应及设计变量的确定

为考虑结构能力的不确定性，参考文献[7]，选取11个结构参数变量作为设计变量，其中核心混凝土4个参数：峰值强度fc,core，峰值强度对应的应变εc,core，屈服强度fcu,core，屈服强度对应的应变εcu,core；保护层混凝土3个参数：峰值强度fc,cover，峰值强度对应的应变εc,cover，屈服强度对应的应变εcu,cover；纵向钢筋3个参数：初始刚度E0，屈服强度fy，钢筋硬化比γ；桥墩几何参数：桥墩直径d.地震动参数采用地面峰值加速度PGA，并结合目前已有研究资料，取桥梁支座位移和墩底截面曲率作为桥梁结构响应.根据桥梁场地条件，以《公路桥梁抗震细则》中的设计反应谱为目标反应谱，从美国太平洋地震工程研究中心(PEER)的最新地震动数据库中选取30条地震动记录，地震动加速度反应谱曲线如图2所示.由文献[13]，采用均匀设计表U30(3013)来构造试验样本对，各结构参数的分布形式见表1.通过Nataf变换考虑结构参数间的相关性，随机变量相关系数参考文献[7]，见表2.

图2 反应谱拟合情况(ξ=5%)Fig.2 The fitting of response spectrum (ξ=5%)

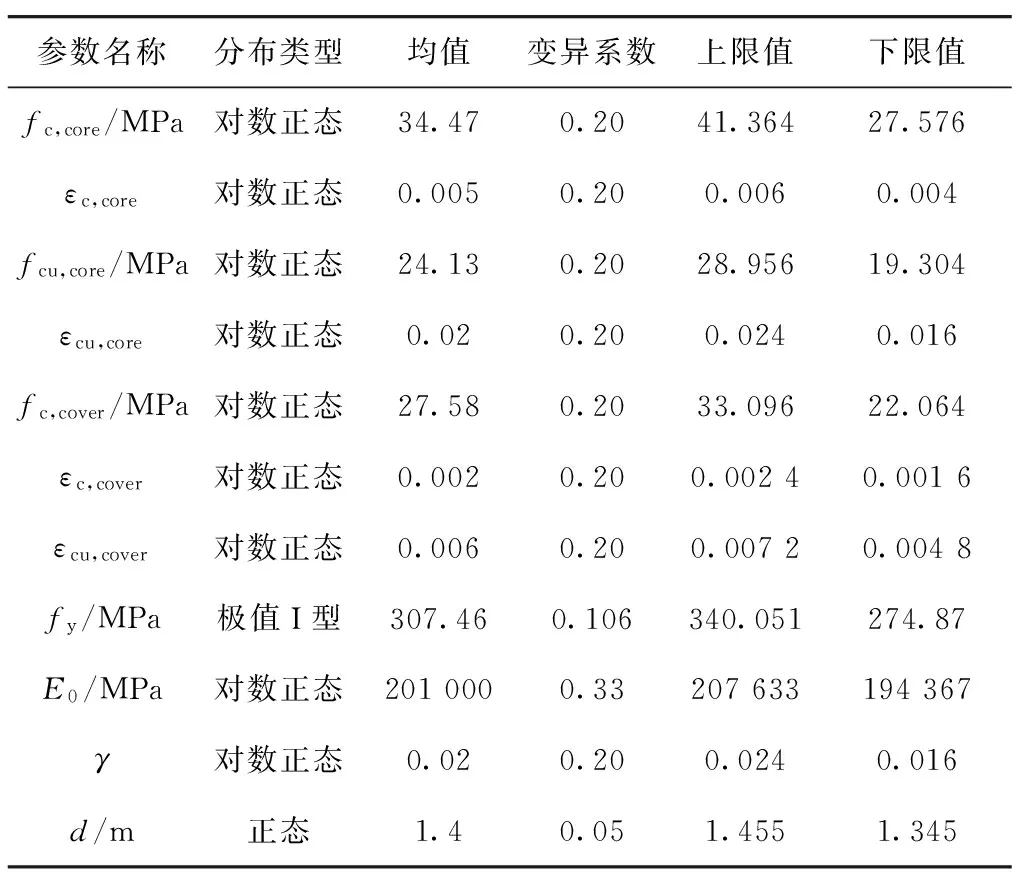
参数名称分布类型均值变异系数上限值下限值fc,core/MPa对数正态34.470.2041.36427.576εc,core对数正态0.0050.200.0060.004fcu,core/MPa对数正态24.130.2028.95619.304εcu,core对数正态0.020.200.0240.016fc,cover/MPa对数正态27.580.2033.09622.064εc,cover对数正态0.0020.200.00240.0016εcu,cover对数正态0.0060.200.00720.0048fy/MPa极值I型307.460.106340.051274.87E0/MPa对数正态2010000.33207633194367γ对数正态0.020.200.0240.016d/m正态1.40.051.4551.345

表2 结构随机变量相关系数表

Tab.2 Correlation coefficient of structure random variables

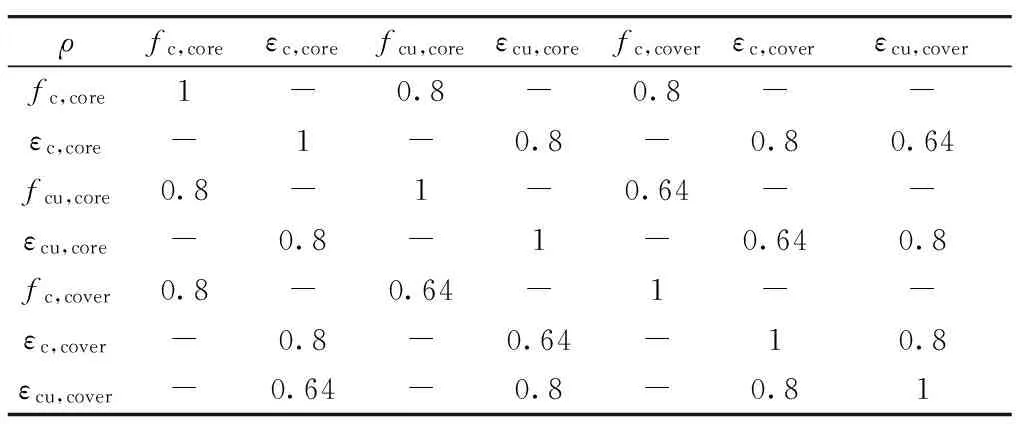
ρfc,coreεc,corefcu,coreεcu,corefc,coverεc,coverεcu,coverfc,core1-0.8-0.8--εc,core-1-0.8-0.80.64fcu,core0.8-1-0.64--εcu,core-0.8-1-0.640.8fc,cover0.8-0.64-1--εc,cover-0.8-0.64-10.8εcu,cover-0.64-0.8-0.81

此处称上述11个结构参数为相关变量组X，其相关系数矩阵为ρ，利用等概率变换原则，根据式(2)对变量组X进行映射变换，将X变换为相关正态变量组Y，并根据式(4)和式(5)确定Y的相关系数矩阵ρ0.由于矩阵ρ0为一对称正定矩阵，可对其进行柯西分解(Cholesky分解)得下三角矩阵L，根据正交变换，则将Y转化为独立的标准正态变量组.此时，可直接对结构参数变量Z进行均匀设计，建立“结构-地震动”样本对.

3 地震需求与易损性分析

3.1 概率地震需求模型(PSDM)

根据“结构-地震动”样本对，基于OpenSees进行30次全过程非线性时程分析，并记录桥梁支座位移和墩柱截面曲率响应的最大值，由最小二乘非线性回归分析得到各构件概率地震需求模型(PSDM)，如图3所示.由图3可知，支座位移的能力需求采用线性拟合较好，而墩柱曲率则采用二次曲线拟合较好.

3.2 地震易损性分析

3.2.1 损伤指标的确定

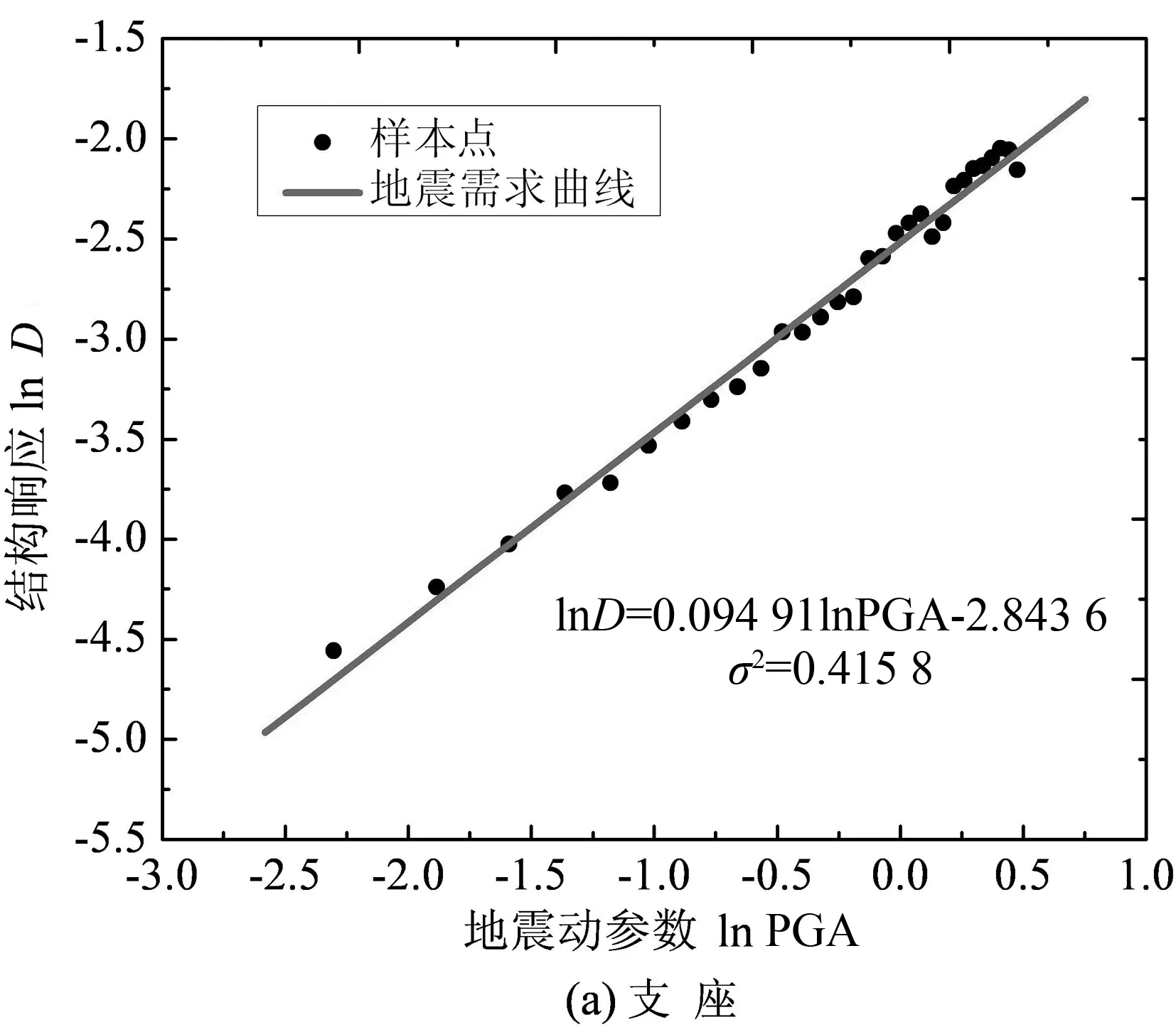
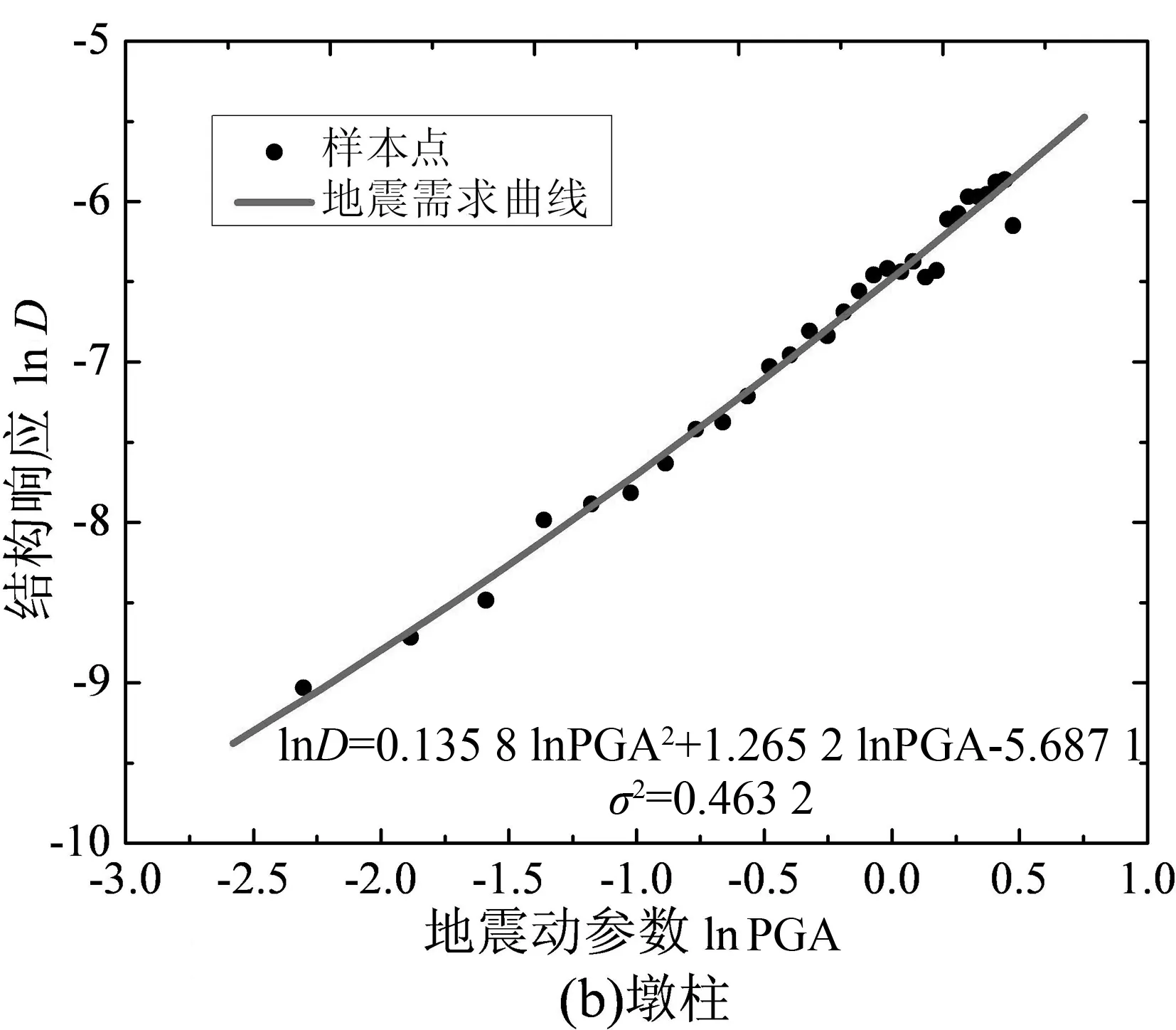
图3 概率性地震需求模型(PSDM)Fig.3 Probabilistic seismic demand model

选择合理的结构响应和性能目标，在基于性能的桥梁抗震设计中尤为重要.易损性分析中采用的破坏准则有4类[17]：强度准则、变形准则、能量破坏准则、变形和能量双重准则.本文采用变形准则，将桥梁损伤状态分为4个等级：1)轻微损伤；2)中等损伤；3)严重损伤；4)完全破坏.其中，墩柱采用曲率延性系数来定义损伤状态，曲率延性系数为墩柱曲率与首次屈服曲率的比值，对各个损伤状态，曲率延性系数的取值[18-19]分别为1.0，2.0，4.0和8.0；对于支座，则采用容许剪切应变作为损伤指标，对各个损伤状态，分别取值为100%，150%，200%和 250%[20]，代入式(12)可计算对应的支座位移.式中：dmax为最大支座位移；∑te为支座橡胶层厚度.定义结构损伤指标见表3.

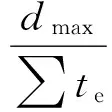
(12)

3.2.2 桥梁构件易损性曲线

易损性曲线可描述在特定地震动强度(IM)作用下结构需求(D)超出结构能力(C)的条件概率[20]，其计算公式如下：

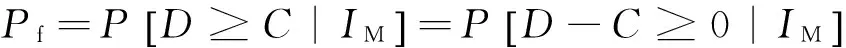
(13)

国内外许多学者在研究中，假定结构的能力极限状态服从对数正态分布[21]，因此结合构件概率地震需求模型(PSDM)可知，易损性仍服从对数正态分布，则可按式(14)计算结构在不同强度水平地震作用下的失效概率.

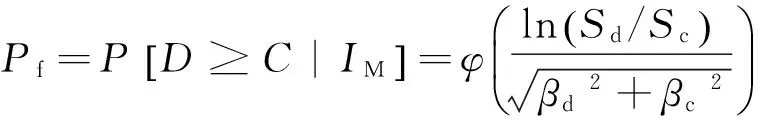
(14)

式中：Sd为结构需求均值；Sc为结构能力均值；βd为结构需求对数标准差；βc为结构能力对数标准差.图4所示为考虑结构参数变量相关性下的桥梁构件易损性曲线.由图4可知，桥梁支座在轻微损伤与中等损伤、严重损伤和完全破坏下失效概率为50%时对应的PGA分别超过了0.6g和1.2g，表明桥梁结构具有足够的抗震能力，墩柱发生严重损伤和完全破坏的失效概率很小，满足我国桥梁抗震设计规范的要求.

表3 不同损伤状态下的损伤指标

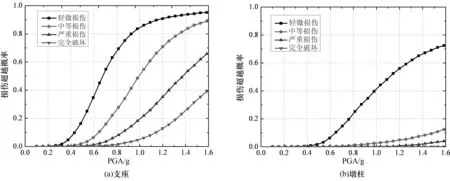
图4 桥梁构件易损性曲线Fig.4 Fragility curves of bridge components

3.2.3 桥梁系统易损性曲线

桥梁是由不同构件组成的复杂组合体系，仅仅依靠构件层次的易损性分析不足以全面评估桥梁整体抗震性能，因此，对桥梁系统层次的易损性分析显得尤为重要.为简化分析，本文采用一阶界限法[22]对桥梁进行系统易损性分析.一阶界限法也称为宽界限法,可对全桥结构系统进行保守估计,由式(15)计算可得桥梁系统层次易损性曲线如图5所示.

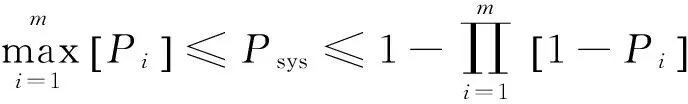
(15)

式中：Psys表示桥梁系统失效概率；Pi表示第i个构件的失效概率；m为构件数.

由图5可看出，轻微损伤、中等损伤、严重损伤和完全破坏下与桥梁系统失效概率为50%时对应的PGA上下界，分别为0.46g和0.68g，0.70g和0.98g，1.0g和1.42g，及1.18g和1.58g.与构件层次易损性曲线相比，桥梁系统比构件更易破坏.同时，一阶界限法计算的上下界限带宽较大，并且随着PGA的增大，这种趋势也会越来越明显.

4 随机变量相关性对易损性分析的影响

由以上分析可知，结合Nataf变换和均匀设计响应面法的本文方法可较好地处理结构参数变量间的相关性，在考虑随机变量相关性的桥梁地震易损性分析中有较好的适用性.为进一步分析结构参数变量相关性对易损性分析的影响，本文分别从结构响应面模型精度、桥梁构件及系统易损性分析等方面进行比较.

4.1 随机变量相关性对结构响应面模型精度的影响

结构参数变量相关性对结构响应面精度的影响，可根据结构响应面的拟合系数R2和修正拟合系数Ra2与1的逼近程度来检验，具体比较见表4和表5.

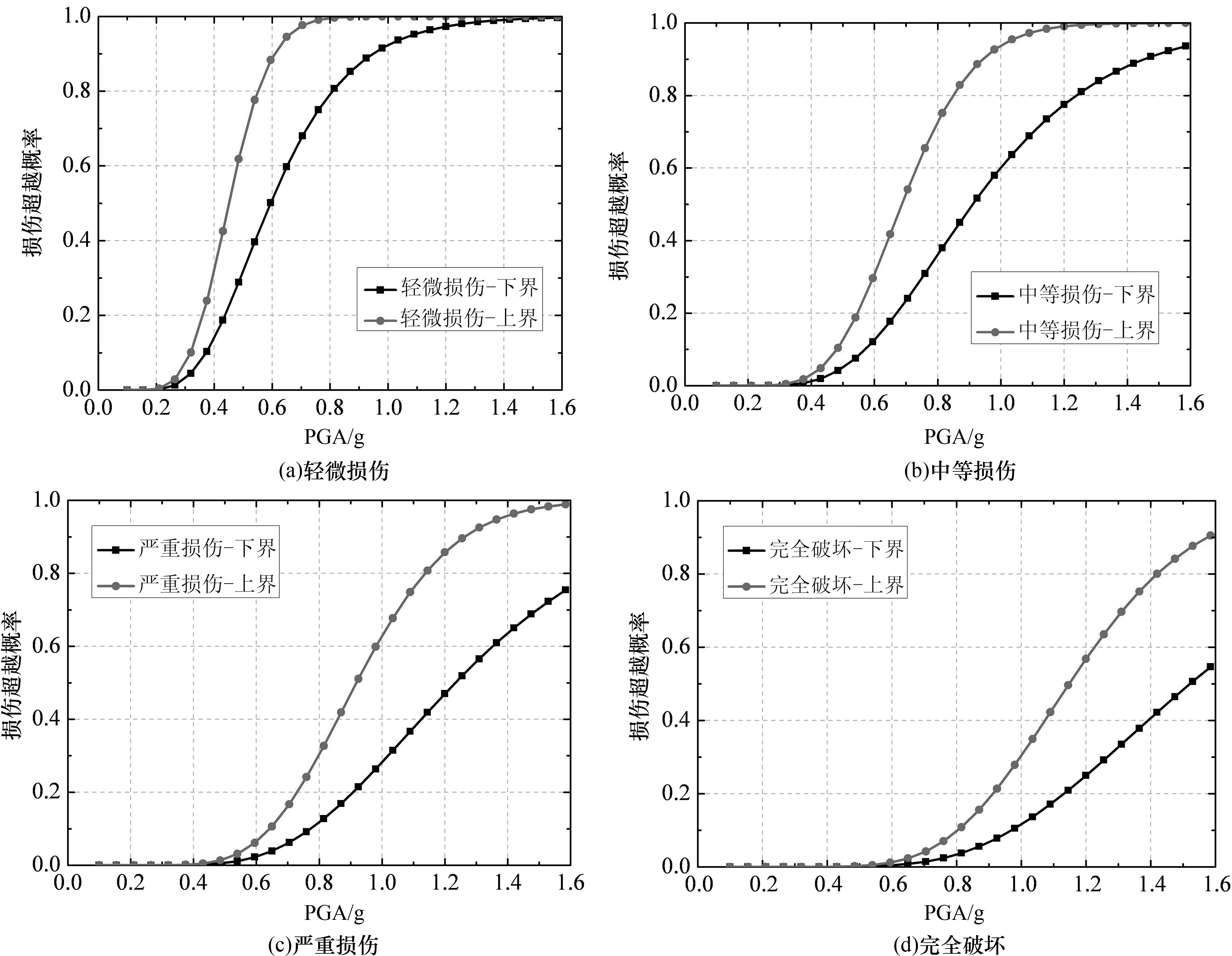
图5 桥梁系统易损性曲线Fig.5 Fragility curves of bridge system

比较项目桥梁支座位移响应面拟合系数均值响应面拟合系数标准差响应面拟合系数均值响应面拟合系数相对值/%标准差响应面拟合系数相对值/%不考虑结构R20.94640.9514100100相关性Ra20.93350.9291100100考虑结构R20.99260.9885104.88103.90参数相关性Ra20.98140.9846105.13105.97

表5 墩柱曲率响应面精度比较

注：R2与Ra2分别为响应面的拟合系数和修正拟合系数；均值和标准差响应面拟合系数相对值分别为考虑与不考虑结构参数相关性的响应面拟合系数的比值.

由表4可知：在桥梁支座位移响应均值和标准差响应面拟合系数方面，与不考虑结构参数相关性情况相比，考虑相关性后，拟合系数R2和修正拟合系数Ra2增加了4%～6%；同理，由表5可看出：在桥梁墩柱曲率响应均值和标准差响应面拟合系数方面，与不考虑结构参数相关性情况相比，考虑相关性后，拟合系数R2和修正拟合系数Ra2增加了4%～5%.因此，考虑结构参数相关性影响后，建立的结构响应面拟合系数有一定程度的增大，与1.0更接近，表明本文方法所建立的响应面能更好地拟合结构真实极限状态函数曲面，可用于评估结构响应特征.

4.2 随机变量相关性对桥梁构件易损性的影响

结构参数变量相关性对桥梁构件易损性分析的影响，可通过考虑与不考虑结构参数相关性情况下构件易损性曲线对比来反映，如图6所示.

图6 结构参数相关性对桥梁构件易损性的影响Fig.6 The influence of correlations of structure random variables on fragility curves of bridge components

由图6可看出，与不考虑结构参数相关性相比，考虑结构参数相关性后，桥梁支座和墩柱的各损伤状态下的失效概率都有一定程度的降低,最大降低幅度约为20%.这表明，考虑结构参数相关性后，桥梁构件地震易损性有一定程度降低，因而，忽略结构参数变量相关性的影响，会低估桥梁构件的抗震性能.

4.3 随机变量相关性对桥梁系统易损性的影响

为检验结构参数变量相关性对桥梁系统易损性的影响，可通过考虑与不考虑结构参数相关性情况下的桥梁系统易损性曲线的对比来反映，如图7所示.

由图7可知，与桥梁构件易损性分析情况相同，考虑结构参数变量相关性后，桥梁系统的各损伤状态下的失效概率均有一定程度的降低，最大降低幅度约为36%.考虑结构参数相关性后，桥梁系统层次地震易损性有一定程度降低，因而，忽略结构参数变量相关性的影响，会低估桥梁整体的抗震性能，故在实际工程中需引起重视.

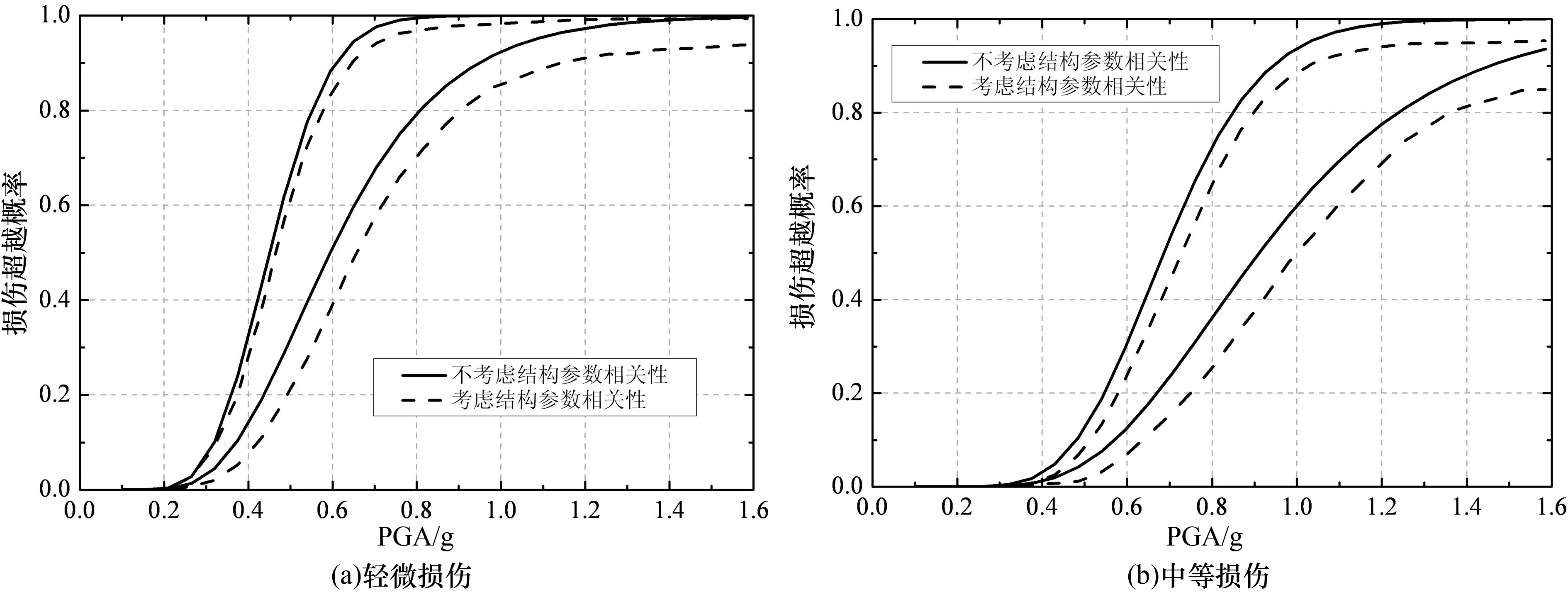
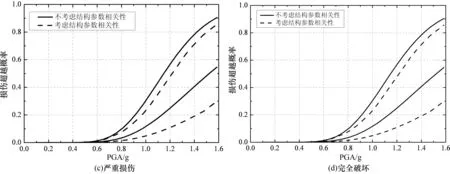
图7 结构参数相关性对桥梁系统易损性的影响Fig.7 The influence of correlations of structure random variables on bridge system fragility curves

5 结 论

1)通过Nataf变换，考虑结构参数变量相关性，结合均匀设计响应面法的本文方法，能综合考虑地震动和结构的不确定性，在桥梁地震易损性分析中有较好的适用性.

2)在考虑结构参数随机性的基础上，本文通过Nataf变换考虑了结构参数相关性，与不考虑结构参数相关性相比，桥梁结构响应面拟合系数增加4%～6%，建立的响应面能更好地对结构真实的极限状态函数曲面进行拟合，可较好地反映结构响应的基本特征.

3)与不考虑结构参数变量相关性相比，考虑变量相关性后，桥梁构件及系统层次各损伤状态下的失效概率均有一定程度的降低，最大降低幅度分别为20%和36%.忽略结构参数相关性的影响，可能会低估桥梁结构在地震作用下的抗震性能.

[1] CASCIATI F，CIMELLARO G P，DOMANESCHI M.Seismic reliability of a cable-stayed bridge retrofitted with hysteretic devices [J].Computers & Structures，2008，86(17)：1769-1781.

[2] BANERJEE S，SHINOZUKA M.Nonlinear static procedure for seismic vulnerability assessment of bridges [J].Computer-Aided Civil and Infrastructure Engineering，2007，22(4)：293-305.

[3] HWANG H，LIU J B，CHIU Y H.Seismic fragility analysis of highway bridges [R].Memphis：Center for Earthquake Research and Information，University of Memphis，2001：28-42.

[4] 李立峰,吴文朋,黄佳梅，等.地震作用下中等跨径RC连续梁桥系统易损性研究[J].土木工程学报，2012，45(10)：152-160.

LI Lifeng，WU Wenpeng，HUANG Jiamei，etal.Study on system vulnerability of medium span reinforced concrete continuous girder bridge under earthquake excitation [J].China Civil Engineering Journal，2012，45(10)：152-160.(In Chinese)

[5] 李立峰,吴文朋,黄佳梅，等.板式橡胶支座地震易损性分析[J].湖南大学学报:自然科学版,2011,38(11)：1-6.

LI Lifeng，WU Wenpeng，HUANG Jiamei，etal.Seismic fragility analysis of laminated rubber bearings[J].Journal of Hunan University：Natural Sciences，2011，38(11)：1-6.(In Chinese)

[6] PANG Y T，WU X，SHEN G Y,etal.Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties[J].Journal of Bridge Engineering，2014，19(4)：04013015-1— 04013015-11.

[7] 沈国煜,袁万城,庞玉涛.基于Nataf变换的桥梁结构地震易损性分析[J].工程力学，2014，31(6)：93-100.

SHEN Guoyu,YUAN Wancheng，PANG Yutao.Seismic fragility analysis of bridge structure based on Nataf transformation [J].Engineering Mechanics，2014，31(6)：93-100.(In Chinese)

[8] 唐和生，范德伟，李大伟,等.基于Info-Gap决策的结构抗震稳健性优化设计[J].湖南大学学报：自然科学版，2015，42(5)：21-28.

TANG Hesheng，FAN Dewei，LI Dawei，etal.Info-Gap decision for the robust seismic design optimization of structures[J].Journal of Hunan University：Natural Sciences，2015,42(5)：21-28.(In Chinese)

[9] LIU P L，KIUREGHIAN A.Multivariate of distribution models with prescribed marginal and covariance [J].Probabilistic Engineering Mechanics，1986，1(2)：105-112.

[10]吴帅兵,张坤,李典庆.相关非正态变量变换时相关性变化对可靠度的影响[J].武汉大学学报:工学版，2011，44(2)：151-155.

WU Shuaibing，ZHANG Kun，LI Dianqing.Effects of correlation change from transformation of correlated abnormal variables on structural reliability [J].Engineering Journal of Wuhan University：Natural Sciences，2011，44(2)：151-155.(In Chinese)

[11]吴帅兵,李典庆,周创兵.结构可靠度分析中变量相关时三种变换方法的比较[J].工程力学,2011，28(5)：41-49.

WU Shuaibing，LI Dianqing，ZHOU Chuangbing.Comparisons among three transformation methods for structural reliability analysis with correlated variables [J].Engineering Mechanics，2011，28(5)：41-49.(In Chinese)

[12]刘敬敏,余波,杨绿峰.Orthogonal 变换与Nataf变换对FORM计算精度的影响分析[J].应用力学学报,2015，32(1)：125-131.

LIU Jingmin，YU Bo，YANG Lüfeng.Effects of Orthogonal and Nataf transformations on the precision of the first order reliability method[J].Chinese Journal of Applied Mechanics，2015，32(1)：125-131.(In Chinese)

[13]胡常福,李辉辉,任伟新,等.基于响应面的新型索拱桥非线性索力优化[J].中南大学学报：自然科学版，2015，46(11)：4267-4273.

HU Changfu，LI Huihui，REN Weixin，etal.Nonlinear cable force optimization of new type arch bridges with diagonal web cables based on response surface method [J].Journal of Central South University：Natural Sciences，2015，46(11)：4267-4273.(In Chinese)

[14]方开泰.均匀设计与均匀设计表[M].北京:科学出版社,1994:1-23.

FANG Kaitai.Uniform design and uniform design table [M].Beijing：Science Press，1994:1-23.(In Chinese)

[15]MAZZONI S，MCKENNA F，SCOTT M H,etal.OpenSees command language manual [M].Berkeley，CA：Pacific Earthquake Engineering Research Center，University of California，Berkeley，2006:36-65.

[16]AVIRAM A，MACKIE K，STOJADINOVIC B.Guidelines for nonlinear analysis of bridge structures in California[R].Berkeley，CA：Pacific Earthquake Engineering Research Center，University of California，Berkeley，2008:3.

[17]STONE W C，TAYLOR A W.Seismic performance of circular bridge columns designed in accordance with AASHTO/CALTRANS standards [M].Alexandria，VA：National Institute of Standards and Technology，1993：102-106.

[18]CHOI E，DESROCHES R，NIELSON B.Seismic fragility curves of typical bridges in moderate seismic zones [J].Engineering Structures，2004，26(2)：187-199.

[19]YANG C S，DESROCHES R，PADGETT J E.Fragility curves for a typical California box girder bridge [C]// Proceedings of TCLEE 2009 ASCE Technical Council on Lifeline Earthquake Engineering Conference：Lifeline Earthquake Engineering in a Multi-hazard Environment.Reston，VA：ASCE，2009：1-12.

[20]PADGETT J E，DESRROCHES R.Methodology for the development of analytical fragility curves for retrofitted bridges [J].Earthquake Engineering and Structural Dynamics，2008，37(8)：1157-1174.

[21]CORNELL C A，JALAYER F，HAMBURGER R，etal.Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines [J].Journal of Structural Engineering，2002，128(4)：526-533.

[22]CORNELL C A.Bounds on the reliability of structure system [J].Journal of Structure Division，ASCE，1967，93(ST1)：171-200.

Bridge Seismic Fragility Analysis Considering RandomVariable Correlations

LI Lifeng†，LI Huihui，XU Kaiduo，HU Sicong

(College of Civil Engineering，Hunan University，Changsha 410082，China)

Combined with uniform design and response surface method and Nataf transformation,an alternative seismic fragility analysis method,which can take the uncertainties of ground motions and structures as well as the correlations of structural random variables into account,was proposed.This study took a continuous girder bridge as case-study.The bridge seismic fragility analysis was performed,considering the dependence and correlations of structural random variables.Meanwhile,the seismic fragility analysis and the accuracy of the response surface model affected by the correlations of structural random variables were analyzed.The analysis result indicates that the proposed method can effectively take the correlations of structural random variables into account.After considering the correlations of the structural random variables,the established response surface can better fit the surface limit state function of structure,the probability failure of bridge in each damage state has a certain degree of reduction,and neglecting the correlations of structural random variables may underestimate the seismic performance of the bridge.

bridge seismic fragility;random variables;correlations;Nataf transformation;uniform design and response surface method

1674-2974(2017)07-0118-10

10.16339/j.cnki.hdxbzkb.2017.07.015

2016-03-15

国家自然科学基金资助项目(51278183), National Natural Science Foundation of China(51278183)

李立峰(1971—)，男，湖南沅江人，湖南大学教授，博士†通讯联系人， E-mail:lilifeng@hnu.edu.cn

U441

A