基于广义回归神经网络的炸药量推算

张龙年张彦春陈立宏张洪国

（1 中国刑事警察学院教务处 辽宁 沈阳 110035；2 中国刑事警察学院研究生处 辽宁 沈阳 110035；3 中国刑事警察学院痕迹检验技术系 辽宁 沈阳 110035）

基于广义回归神经网络的炸药量推算

张龙年1张彦春2陈立宏3张洪国3

（1 中国刑事警察学院教务处 辽宁 沈阳 110035；2 中国刑事警察学院研究生处 辽宁 沈阳 110035；3 中国刑事警察学院痕迹检验技术系 辽宁 沈阳 110035）

炸药量推算在爆炸现场分析中具有重要作用。利用炸坑痕迹的3个表观量化特征参量，建立了基于广义回归神经网络的炸药量推算方法，并以野外爆炸实验数据为基础，进行炸药量推算结果与实际值的比较。结果显示，此方法在根据土介质炸坑痕迹推算炸药量方面能够达到比较准确的推算效果，尤其在软粘土及中硬粘土介质中，对炸药量的推算具有较高的准确性和可靠性。

炸坑痕迹 炸药量 广义回归神经网络

1 引言

爆炸案件现场炸药量推算是一个复杂的问题，这是由爆炸现场的复杂性及爆炸现场痕迹产生影响因素较多所决定的。目前，常用的炸药量推算方法有经验判断法及经验公式推算法，其科学性和准确性都有待于进一步提高。

本文根据炸坑痕迹的量化特征，建立了一种用于解决地面接触爆炸情况下，炸药量推算问题的方法。该方法依托广义回归神经网络（Generalized Regression Neural Network，GRNN）算法，利用炸坑痕迹的3个表观量化特征参量，建立了炸药量推算模型。由于广义回归神经网络获取数据之间关系的方法不同于插值和拟合，而是直接以采样或计算得来的数据对网络进行修改，不需要重新计算参数，因此在分类能力、逼近能力和学习速度上都有较强的优势，对不稳定数据及样本数据缺乏的数据预测效果也比较好[1]，进而决定了该模型能够对炸药量进行准确地推算，保证了推算方法的科学性和可行性。

2 基于GRNN炸药量推算方法的建立

GRNN最早由美国学者Donald F. Specht在1991年提出[2]，是一种基于非线性回归分析理论建立的神经网络模型，其原理源于数理统计中概率论的思想：当用作函数逼近时，网络输出可理解为网络输入的回归函数；当用作分类时，其可理解为相应类别的后验概率[3]。GRNN的网路结构共有4层，分别为输入层、模式层、求和层和输出层，如图1所示。

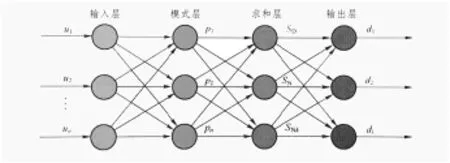
图1 GRNN网络结构图

基于GRNN的炸药量推算方法是智能推算的神经网络法，其核心是采用广义回归神经网络的系统辨识理论对爆炸作用后产生的炸坑痕迹表观量化特征参量进行分析。本文研究目的是推算炸药量，因此炸药量即为此智能推算的神经网络输出，而炸坑痕迹表观量化特征参量即为该神经网络的输入。爆炸后产生的炸坑痕迹是推算炸药量最常用的痕迹，而土介质类型、炸坑直径及炸坑深度数据也是炸坑痕迹最直观的可量化数据[4]，相比于压缩壁直径和深度更容易测量。因此，建立基于GRNN炸药量推算方法，首先就是利用炸坑实验中的3个表观量化特征参量（土介质爆炸作用系数、炸坑直径和炸坑深度）以及炸药量数据，通过广义回归神经网络算法对这些数据进行同步处理，其中炸坑直径、炸坑深度和土介质爆炸作用系数作为神经网络模型的输入层，炸药量作为神经网络的输出层，然后通过训练得到这几个因素构成的网络模型，找出输入与输出之间的特征关系从而进行推算应用，即当通过输入实测炸坑得到的3个表观量化特征参量即可获得反分析的解[5]。

推算模型的基本构建流程，具体可以分为以下4个步骤：

（1）产生训练样本数据集和测试样本数据集。在产生训练样本数据集及测试样本数据集时，首先需要考虑训练集和测试集样本的数量，本文以地面接触炸坑实验数据中的39组实验数据作为训练样本数据集，以另外11组地面接触炸坑实验数据作为测试样本数据集，如表1所示。其中，M为实际炸药量； K为介质爆炸作用系数（K为经验系数通常取值7~10）[6]，硬介质地面取值偏小，软介质地面取值偏大；D2为炸坑直径；h2为炸坑深度。

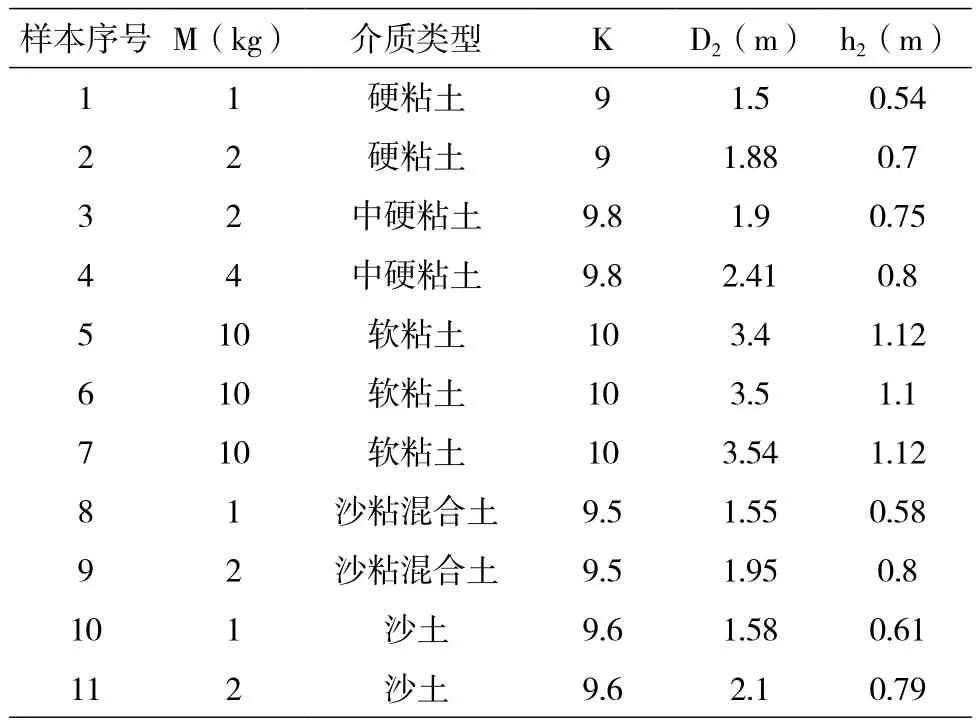
表1 测试样本数据

其次还需要考虑到异常数据样本是否会对模型的建立产生影响，建议对异常数据样本做剔除处理后再建模。表1中K的取值是在基于经验公式推算炸药量的方法中，误差最小的条件下进行选择的。在本文研究的炸药量推算方法中，介质爆炸作用系数K的不同取值，可以等同于对不同土介质类型的分类。

（2）建立GRNN神经网络。在Matlab环境下，采用Matlab语言编写算法计算程序。以炸坑实验数据中炸坑直径D2和炸坑深度h2，以及土介质爆炸作用系数k作为神经网络模型的输入层，炸药量W作为神经网络的输出层，应用Matlab神经网络工具箱构建推算模型，W =M (D2,h2,k)。

（3）一旦输入层与输出层变量的函数关系M (D2,h2,k)确定，输入测试样本集的炸坑痕迹的测量值（炸坑直径D2、炸坑深度h2、土介质爆炸作用系数k）后，将通过模型M (D2,h2,k)输出我们所关注的炸药量W，从而实现炸药量推算的需求。

（4）将推算结果与实际值进行比较，检测推算模型的推算效果。

3 结果与分析

本研究中炸坑实验使用的炸药均为TNT炸药，其他类型的炸药可以通过公式换算成等效的TNT当量。根据以上炸药量推算方法确定的输入和输出，将39组实验数据作为训练样本，通过神经网络对其进行训练得到炸药量推算网格模型，然后把表1中11组实验数据作为测试样本输入此网络模型进行推算，推算结果如表2所示。

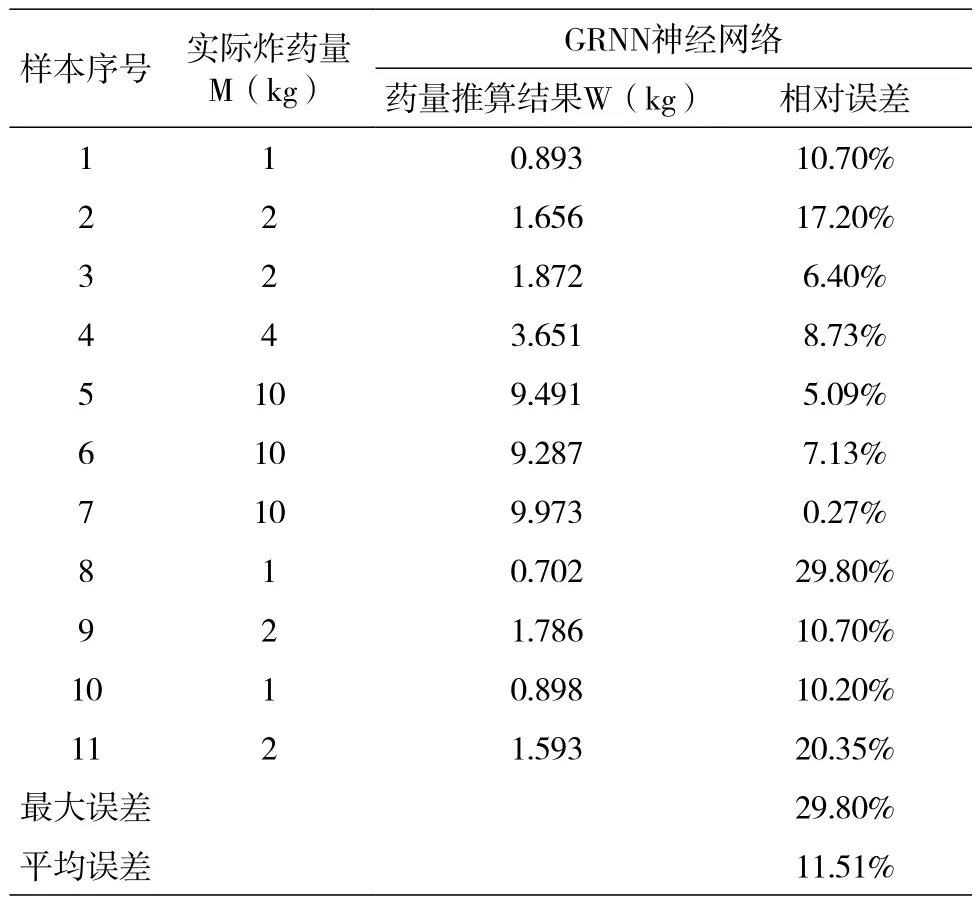
表2 GRNN推算结果

分析表2数据可以看出，11组测试样本的推算炸药量与实际炸药量相对误差平均值为11.51%，其中测试样本3～7组炸药量推算值的相对误差最为理想，均未超过10%，说明在软粘土及中硬粘土介质中该炸药量推算方法有更好的适用性。

为检验该推算方法的泛化能力与可靠性，将推算结果和实际数据进行拟合比较，结果如图2所示。

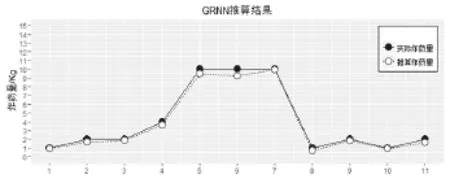
图2 GRNN推算和实际炸药量拟合图

由上图比较分析可以看出，推算炸药量折线图与实际炸药量折线图，除在个别测试样本数据推算结果不理想外，总体上基于GRNN对炸药量进行推算具有比较高的准确性，推算模型可靠性也较高，推算结果与实际值基本吻合。对于个别测试样本数据推算结果不理想的原因，笔者认为在对爆炸后炸坑数据（炸坑直径，炸坑深度）的测量中存在一定人为误差，提高测量工具精度及测量次数可以有效避免测量误差的形成进而减少较大推算误差的形成。此外虽然GRNN对于样本缺乏的数据具有较好的推算效果，但是充足的样本量必然会提高GRNN模型训练精度，因此通过增加样本数据量提升GRNN模型推算精度也是可行的。

4 结论

本文提出的利用炸坑痕迹的3个表观量化特征参量并基于广义回归神经网络而建立的炸药量推算方法，经过11组实验样本数据的测试，结果表明：基于广义回归神经网络的炸药量推算方法，在地面接触爆炸条件下具有较好的可行性，尤其在软粘土及中硬粘土介质中，炸药量推算结果最好。对于近地面埋入或悬空爆炸的情况，在后续的研究中需要将炸药埋深或悬空高度与炸药量一同作为神经网络的输出层，建立新的样本训练模型，进而扩大该炸药量推算方法的适用范围。

[1]王小川,史峰,等.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:67-71.

[2]Specht D E.The general regression neural networkrediscovered[J].Neural Network,1993(7):1033-1034.

[3]杨杰,占军,等.MATLAB神经网络30例[M].北京:电子工业出版社,2014:94-97.

[4]张彦春,罗亚平,等.土介质炸点痕迹反演爆源特征的研究[J].安全与环境学报,2012(2):261-264.

[5]张涛,张锦龙.基于GRNN神经网络的货运量预测研究[J].物流科技,2014(10):138-141.

[6]张彦春,张洪国.爆炸现场勘验与分析技术[M].北京:中国人民公安大学出版社,2013:197-200.

（责任编辑：于 萍）

X932

A

2095-7939（2017）04-0069-03

10.14060/j.issn.2095-7939.2017.04.012

2017-02-16

张龙年（1988-），男，辽宁沈阳人，中国刑事警察学院教务处研究实习员，主要从事实践教学管理和爆炸现场勘验与分析技术研究。