一种卫星快速姿态机动及稳定控制方法

冯佳佳北京控制工程研究所，北京100190

一种卫星快速姿态机动及稳定控制方法

冯佳佳＊
北京控制工程研究所，北京100190

针对小卫星快速姿态机动要求，提出一种基于粒子群优化（PSO）算法的卫星快速姿态机动及稳定控制方法。该方法首先以粒子种群的初始位置为卫星机动加速阶段终点时刻进行路径规划，然后针对规划好的路径利用维持跟踪控制进行姿态机动，在路径末端利用黄金分割和逻辑微分进行稳定控制，最后以卫星姿态到达目标角度且保持稳定的时间作为适配值，寻找出一条在该组合控制方法和限制条件下的最优路径进行姿态机动及稳定控制。该控制方法能够根据星体的实际动力学特性、环境特征、限制条件及控制性能进行最优机动及稳定控制。将该方法应用到小卫星的姿态机动控制中，仿真结果表明该方法有效。

姿态控制；快速机动；粒子群优化算法；挠性卫星；稳定

快速姿态机动及稳定控制作为小卫星的关键技术之一，日益为学者们所关注。但由于星体不仅具有大挠性附件或本身就是挠性结构，而且有液体晃动和消耗，有振动源，数学方程很复杂，具有非线性、高阶、时变等特性［1］，使得卫星的姿态控制问题成为一个非线性控制问题［2］，这对大角度快速机动及快速稳定性产生了严重的影响［3－4］。

目前，关于卫星快速姿态机动及稳定控制方法已经有一些研究成果［5－12］。一般情况下，为了尽快完成卫星的大角度机动，在机动过程中希望星体以最大角速度运动，但卫星的机动速度受到执行机构提供的最大力矩和角动量限制，此外，在到达目标机动角度后，由于星体特征变化以及外部扰动，星体也很难快速稳定［3］。在执行机构能力受限和角速度测量受限的情况下，大角度快速机动运动路径一般可以分为加速、匀速和减速3个运动阶段；根据机动角度幅值和最大角速度幅值，可能不存在匀速阶段。理想状况下的运动路径如图1所示，设完整的机动时间为tf，在t∈（0，0.5tf）时，角速度v进行加速，其对应的力矩大小为umax，在t∈（0.5tf，tf）时，角速度v进行减速，其对应的力矩为－umax，在t＞tf时，角速度v＝0，对应的力矩u＝0，其中，角速度所围成的面积为机动目标角度α。但实际过程中面临3个主要问题需要解决：1）由于卫星所建模型不精确及其存在挠性结构，在机动及稳定过程中，如何设计控制律使星体快速机动并且保持稳定，文献［13］指出，由于模型建立的不精确，如果存在外扰激发未建模动态，那么使用传统的控制方法将使控制系统的性能大幅度下降，甚至失稳；2）在星体特征变化、外部扰动、执行机构能力受限等其他条件下，如何确定最优机动路径，使其在所设计的控制律下能进行快速机动并且保持稳定；3）所设计的机动及稳定控制方法具有通用性，符合航天控制发展趋势［14］。

图1 理想状况下的运动路径Fig.1 Ideal path

本文以具有大角度快速机动要求的小卫星为对象，研究了具有多输入－多输出的非线性系统最优控制问题，提出了一种基于PSO算法［15－17］的卫星快速姿态机动及稳定控制方法。该方法首先以粒子种群的初始位置为卫星机动加速阶段终点时刻进行路径规划，然后针对规划好的路径利用维持跟踪控制进行姿态机动，在路径末端利用黄金分割和逻辑微分进行稳定控制，最后以卫星姿态到达目标角度且保持稳定的时间作为适配值，寻找出一条在该组合控制方法和限制条件下的最优路径进行姿态机动及稳定控制。

1 问题描述

具有挠性附件三轴稳定卫星的动力学模型可以描述为［18］：

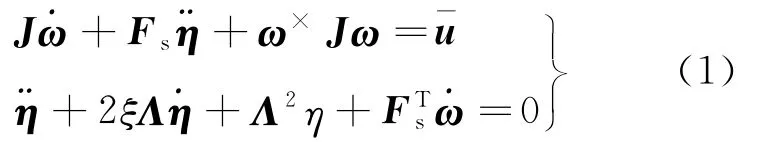
式中：ω∈R3为航天器的角速度在本体坐标系下的描述；J∈R3×3为航天器的转动惯量；η∈Rm为挠性附件模态向量；Fsj∈R3×m为挠性模态与航天器中心刚体的耦合系数矩阵；ξ为挠性附件的阻尼系数，工程上一般取0.005；Λ＝为挠性模态频率向量，Λ2＝为作用于卫星的外力矩，包括控制力矩u和环境干扰力矩d；ω×为卫星角速度的反对称阵。

定义卫星三轴欧拉姿态角q（t）＝［φ，θ，ψ］T，其中φ，θ，ψ分别为航天器的滚动、俯仰和偏航角，其角速度在星体坐标系中的表达式为：

其中，当q在一定区间变化时，B（q）是可逆阵，本文只研究B（q）可逆的情况。

当采用1－2－3转序时，

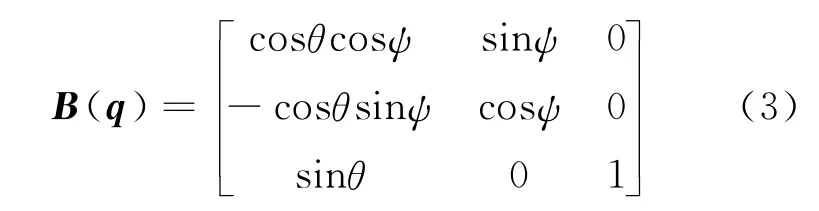
控制任务是：卫星从初始姿态q（0）＝0，˙q（0）＝0快速机动到q（tf）＝α，˙q（tf）＝0，并且快速保持稳定，其中α为机动目标角度。

2 快速姿态机动及稳定控制实现

2.1 控制方法设计

由式（1）可知：

则式（7）可变为：

需要说明的是，当对式（8）进行离散时，采样时间Ts需要满足一定的条件，即满足采样定理、连续系统离散化保持原系统能控及控制精度要求，这样由式（8）可以经过离散得到式（9），且性能保持不变［13］。

对式（9）进行变换得：

其中，递推最小二乘公式为：

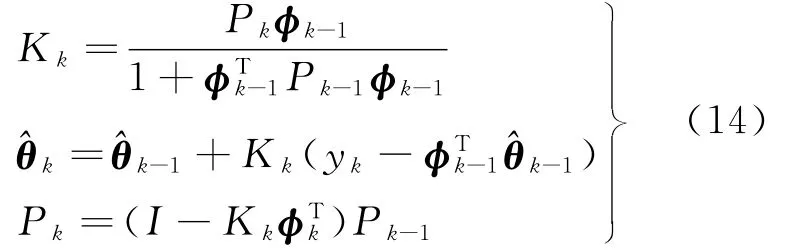
所以维持跟踪控制为：

式中：qr（k）为星体机动规划路径；q（k）为星体机动过程中的实际机动路径。

黄金分割控制为：

式中：l1＝0.382；l2＝0.618；e（k）为卫星机动角度和目标角度的差值。

逻辑微分控制为：

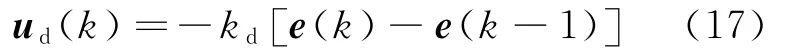
由于：

因此，可以实现稳定跟踪控制。

事实上，由文献［13］可知，式（11）满足特征建模原理，因此，由式（11）可以推导出式（15）～式（17），并使其成立，且当控制器参数＾f1，＾f2，＾g0保持在一定的闭凸集内，所设计的控制器均能保持稳定。

由于维持跟踪控制具有较强的跟随控制能力，它能够根据星体的实际动力学特性和机动路径进行最优机动控制，因此选择维持跟踪控制作为姿态机动阶段的控制方法，黄金分割控制和逻辑微分控制具有较强的稳定能力，它能够有效克服星体特征变化及外部干扰，因此在机动路径末端，选择黄金分割和逻辑微分进行稳定控制。

则所设计的控制方法为：

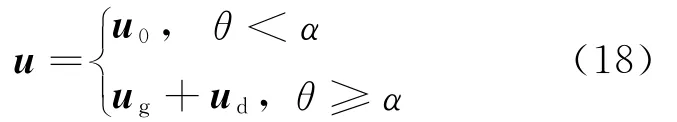
式中：θ为机动角度；α为目标角度。

2.2 基于PSO算法的路径规划

由于星体在机动过程中受到外部扰动、星体特征变化以及其他限制条件，因此，在机动及稳定过程中，需要根据星体的实际情况进行最优路径规划。

粒子群优化算法（PSO）是一种基于种群的仿生随机优化方法，是一种典型群智算法。其最大的优点是实现简单，全局搜索能力强，应用广泛，可以广泛应用于非线性、不可微、多极值、高维函数的优化问题。

PSO算法为：

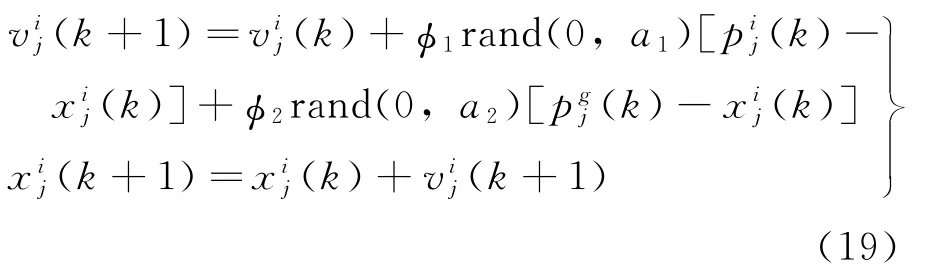
式中：i＝1，2，…，m，为粒子的编号；j＝1，2，…，n，为n维向量的第j个分量；xi（k）＝［xi1，xi2，…，xin］T，为n维位置向量；pi（k）＝［pi1，pi2，…，pin］T，为n维最优位置向量；vi（k）＝［vi1，vi2，…，vin］T为n维速度向量，fix（k）为相应的x适配值；pi（k）表示该粒子迄今所获得的具有最优适配值fip（k）的位置；φ1、φ2分别为控制个体认知分量［pij（k）－xij（k）］和群体社会分量［pgj（k）－xij（k）］相对贡献的学习率，g表示具有迄今全局最优适配值fp（k）的粒子编号；rand（0，a1）与rand（0，a2）分别产生［0，a1］、［0，a2］之间的随机参数，其中a1、a2为相应的控制参数［19］。

在实际应用中，卫星机动受到多种物理限制，如控制输入有界、星体角速度限制等，分别被描述为：

式中：umax为最大输出力矩；vmax为最大星体角速度。

当星体角速度限制为主要限制条件时，理想情况下机动角速度满足：

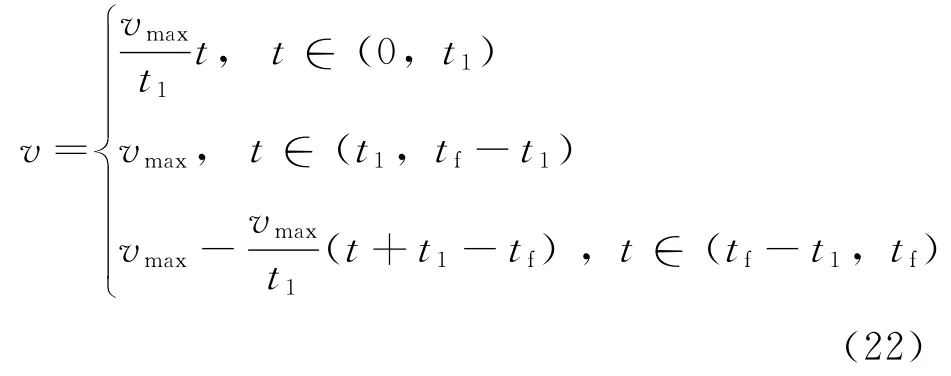
式中：t1为机动加速阶段终点时刻；tf为完成机动路径的总时间。且有：

此时，若机动目标角度为α，则满足：

当控制输入有界为主要限制条件时，理想情况下机动角速度满足：

式中：vM为在控制输入有界情况下星体机动过程中的最大角速度，且vM≤vmax；t1为机动加速阶段终点时刻。

此时，若机动目标角度为α，则满足：

因此，对于给定的机动目标角度α，根据式（22）～式（26）可知，每一个t1都对应着一条机动路径，因此可以选取粒子种群的初始位置为卫星机动加速阶段终点时刻t1进行路径规划。而对于每一条规划出的路径，在限制条件下，利用所设计的控制方法都会有一个完成姿态机动并且保持稳定的时间t，选择f（k）＝t作为适配值，寻找出合适的t1使f（k）最小。

3 仿真校验

为了验证该方法的有效性，进行数学仿真。仿真软件为MATLAB R2013a；卫星的转动惯量为：

挠性翼板一阶频率为2.23Hz，阻尼为0.005，耦合系数矩阵为［0.000 41，3.833，0］；干扰力矩为：

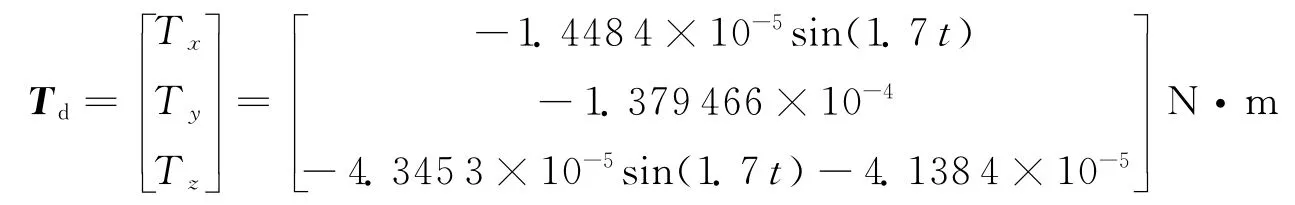
该仿真控制的目的是将卫星从初始姿态q0＝［0，0，0］T，˙q0＝［0，0，0］T，机动到目标姿态qd＝［π／3，0，0］，˙qd＝［0，0，0］T。

采样时间为t＝0.01s，控制力矩采用0.1N·m的限幅，最大星体角速度为0.05rad／s，姿态稳定精度为10－5rad。

取粒子种群数为m＝20，迭代次数n＝20，a1＝a2＝0.8，种群的初始位置随机生成，个体认知和社会群体分量的权重为φ1＝φ2＝1。

仿真结果如图2～图8所示。

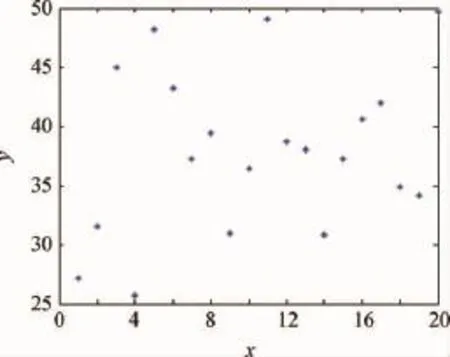
图2 初始粒子群个体位置Fig.2 Initial particle swarm individual position

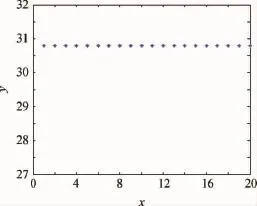
图3 经20步迭代后粒子群的个体Fig.3 After 20steps iterative particle swarm of individuals

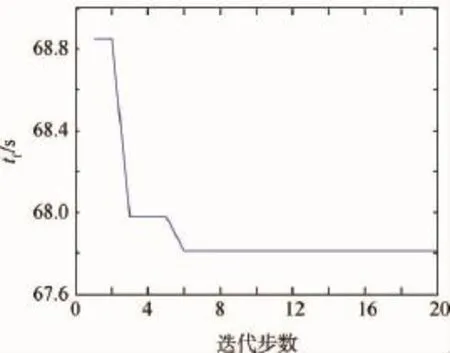
图4 最优适配值分布曲线Fig.4 Optimal adaptation value distribution curve

图5 卫星姿态角波形曲线Fig.5 Satellite attitude angle waveform curve

图6 控制力矩曲线Fig.6 Control torque curve

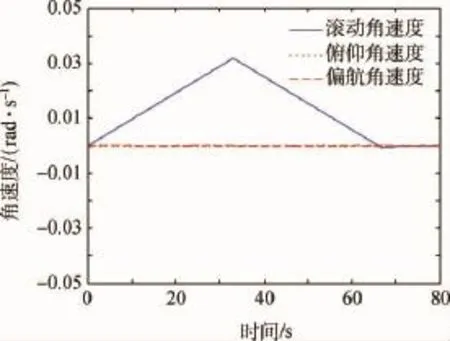
图7 卫星姿态角速度波形曲线Fig.7 Satellite attitude angular velocity waveform curve

图2 为初始种群的位置，其中横坐标表示粒子的序号，纵坐标表示粒子的位置，即卫星机动加速阶段的终点时刻t1；图3为经过20步迭代后的t1，可以看出经过20步迭代后，寻找出了合适的t1；图4为最优适配值曲线，即卫星完成姿态机动并且保持完成的时间t，可以看出迭代6次后，时间t维持不变；图5为卫星姿态角波形曲线；图6为控制力矩曲线；图7为卫星姿态角速度波形曲线；由图5～图7可以看出卫星机动过程与图1所示的机动过程基本一致，因为卫星到达目标角度后需要进行稳定控制，因此控制力矩曲线在机动路径末端会存在小波动；图8为翼板模态坐标曲线，可以看出卫星机动过程中，翼板振动较小。

图8 翼板模态坐标曲线Fig.8 Panel′s modal coordinates curve

由仿真结果可以得出，本文提出的控制方法能够实现卫星姿态的快速机动以及稳定控制。该控制方法相对于常规的控制方法，由于它能够根据系统的实际动力学特性和控制要求选择最优的路径进行姿态机动及稳定控制，因此，在机动时间和控制性能上均优于常规的控制方法。

4 结束语

维持跟踪控制、黄金分割控制、逻辑微分控制和PSO算法均属于智能算法，将它们有效的结合，能够根据星体的实际动力学特性、环境特征和控制性能进行快速的姿态机动及稳定控制，同时，该方法具有通用性，可以将其应用于离线计算的卫星姿态机动及稳定控制中。

（

）

［1］ 吴宏鑫.工程实际中的控制理论和方法的研究与展望［J］.控制理论与应用，2014，31（12）：1626－1631.WU H X.Research and prospect on the control theory and method in the engineering［J］.Control Theory＆Applications，2014，31（12）：1626－1631（in Chinese）.

［2］ SCRIVENER S，THOMPSON R.Survey of time optimal attitude maneuver［J］.Journal of Guidance，Control，andDynamics，1994，17（2）：225－233.

［3］ 雷拥军，谈树萍，刘一武.一种航天器姿态快速机动及稳定控制方法［J］.中国空间科学技术，2010，30（5）：48－53.LEI Y J，TAN S P，LIU Y W.Spacecraft control method for fast attitude maneuver and stabilization［J］.Chinese Space Science and Technology，2010，30（5）：48－53（in Chinese）.

［4］ 孙多青，吴宏鑫.多变量线性时变系统的特征模型及自适应模糊控制方法［J］.宇航学报，2005，26（6）：677－681.SUN D Q，WU H X.Characteristic modeling and adaptive fuzzy control method of MIMO higher－order linear time－varying systems［J］.Journal of Astronautics，2005，26（6）：677－681.

［5］ BONG W.Rapid multimarket acquisition and pointing control of agile spacecraft［J］.Journal of Guidance，Control，and Dynamics，2002，25（1）：96－104.

［6］ DYWER A W.Variable－structure control of spacecraft attitude maneuver［J］.Journal of Guidance，Control，and Dynamics，1988，11（3）：262－270.

［7］ GUAN P，LIU X J，LIU J Z.Adaptive fuzzy sliding model control for flexible satellite［J］.Engineering Application of Artificial Intelligence，2005，18：451－459.

［8］ KUSUDA Y，TAKAHASHI M.Feedback with nominal inputs for agile satellites using control moment gyros［J］.Journal of Guidance，Control，and Dynamics，2011，34（4）：1209－1218.

［9］ LEE B H.Time optimal attitude maneuver strategies for the agile spacecraft with reaction wheels and thrusters［J］.Journal of Mechanical Science and Technology，2005，19（9）：1695－1705.

［10］ BILIMORIA K D，WIE B.Time－optimal three－axis reorientation of a rigid spacecraft［J］.Journal of Guidance，Control，Dynamics，1993，16（3）：446－452.

［11］ 周伟敏，组立业，朱庆华.一种基于大力矩飞轮的敏捷卫星路径规划的姿态机动控制方法［J］.空间控制技术与应用，2014，40（2）：37－41.ZHOU W M，ZU L Y，ZHU Q H.Anattitude maneuver control method based on path planning for agile satellite with large torque flywheels［J］.Aerospace Control and Application，2014，40（2）：37－41（in Chinese）.

［12］ 王焕杰，金磊，贾英宏.基于混合执行机构的敏捷卫星姿态机动控制［J］.空间控制技术与应用，2015，41（6）：19－24.WANG H J，JIN L，JIA Y H.Agilesatellite attitude maneuver control using hybrid actuators［J］.Aerospace Control and Application，2015，41（6）：19－24（in Chinese）.

［13］ 吴宏鑫，刘一武，刘忠汉，等.特征建模与挠性结构的控制［J］.中国科学（E辑），2001，31（2）：137－149.WU H X，LIU Y W，LIU Z H，et al.Control of characteristic modeling and flexible structures［J］.Science in China（Series E），2001，31（2）：137－149（in Chinese）.

［14］ YANG J C.Development of intelligent autonomous control technology for the Chinese space program［C］.IFAC，International Conference on Intelligent Autonomous Control in Aerospace 95，Beijing，August 14－16，1995.

［15］ SUGANTHAN P N.Particle swarm optimizer with neighborhood operator［C］∥Proceedings of the 1999 Congress on Evolutionary Computation，1999.

［16］ LAZINICA A.Particle swarm optimization［M］.［s.l.］：Tech Education and Publishing，2009.

［17］ CARLISLE A，DOZIER G.An off－the－shelf PSO［C］∥Proceedings of the 2001Workshop on Particle Swarm Optimization，Indianapolis，2001：1－6.

［18］ 屠善澄.卫星姿态动力学与控制［M］.北京：宇航出版社，2005.TU S C.Satellite attitude dynamics and control［M］.Beijing：Aerospace Press，2005（in Chinese）.

［19］ 孙增圻，邓志东，张再兴.智能控制理论与技术［M］.北京：清华大学出版社，2011.SUN Z Q，DENG Z D，ZHANG Z X.Intelligent control theory and technology［M］.Beijing：Tsinghua University Press，2011（in Chinese）.

（编辑：高珍）

Satellite control method for fast attitude maneuver and stabilization

FENG Jiajia＊
Beijing Institute of Control Engineering，Beijing 100190，China

In view of the small satellite fast attitude maneuver，a satellite control method for fast attitude maneuver and stabilization based on particle swarm optimization（PSO）was proposed.First，this method does the path planning which the initial position of particle population is as the finish time for satellite maneuver acceleration period；then in this path planning the maintenance tracking control was used for tracking，and in the end of the maneuver path，the golden section control and logic differential control were used to make stability control；at last，the time of satellite attitude maneuver to target angle and stable was taken as adaptive value to find out an optimal path in the conditions of this combined control method and other limit to attitude maneuver and stability control.This control method can do optimal maneuver and stability control according to the actual dynamic characteristics，environmental characteristics of the astral，constraints and control performance.Applying this method to the small satellite attitude control，simulation results show the effectiveness of the method.

attitude control；fast maneuver；partical swarm optimization；flexible satellite；stabilize

TP373

A

10.16708／j.cnki.1000－758X.2017.0058

2016－12－19；

2017－03－13；录用日期：2017－06－29；网络出版时间：2017－08－11 13：18：22

http：∥kns.cnki.net／kcms／detail／11.1859.V.20170811.1318.008.html

国家自然科学基金（61333008）

＊通讯作者：冯佳佳（1986－），男，博士研究生，fengjiajia888＠163.com，研究方向为航天控制

冯佳佳.一种卫星快速姿态机动及稳定控制方法［J］.中国空间科学技术，2017，37（4）：34－40.FENG J J.

Satellite control method for fast attitude maneuver and stabilization［J］.Chinese Space Science and Technology，2017，37（4）：34－40（in Chinese）.