组合体机动中可变形桁架运动规划研究

邓雅，张锦江北京控制工程研究所，北京100190

组合体机动中可变形桁架运动规划研究

邓雅，张锦江＊
北京控制工程研究所，北京100190

目前对空间组合体中可变形桁架（Variable Geometry Truss，VGT）运动规划问题的研究集中在各级均为单自由度或离散二状态等简单结构的情形，未解决所有可调长度杆都能够自由运动的复杂结构运动规划问题。文章根据组合体的几何关系，建立了递推位姿运动学模型，再由自由漂浮系统动量守恒，建立了微分运动学模型。给出了单级VGT变化序列与运动时间分开设计的两步运动规划方法，并在优化目标中加入能量项，给出了多级冗余VGT的运动规划方法。最后通过仿真验证了算法的有效性，在算例中优化指标为J＝0.879 8，该方法对以VGT作为空间操作机构的组合体研究具有一定工程指导意义。

空间操作机构；可变形桁架；运动规划；遗传算法；运动学建模；组合体机动

Key words：space operation structure；variable geometry truss；motion planning；genetic algorithm；kinematic modeling；multibody maneuvering

中国将于2020年前后建成空间站，它由核心舱、实验舱等舱段构成［1］，舱段之间通过空间操作机构连接。空间操作机构通常由机械臂实现，但限于质量和任务，通常采用轻型材料、细长结构，在操作大负载时柔性特征明显［2］。可变形桁架（Variable Geometry Truss，VGT）也是空间操作机构的一种，是指桁架空间结构确定，而部分杆件长度可连续调节的自适应结构［3］。由于VGT通常安装较多分布式的传感器和执行器，与传统串联机械臂相比，可以提供更强的灵活性，同时，其串并联混合结构具有更强的刚性，能够实现空间建造、组装和运输等功能，在空间机器人、蛇形臂等领域都有应用［4－5］。

已有学者针对VGT的建模和控制等问题进行了研究工作。文献［6－8］基于工作空间密度的概念和扩散过程给出了离散二状态平面VGT的建模和控制方法。文献［3，9］提出了一组用3个角度值作为变量描述VGT非线性几何模型的方程。在此基础上，文献［4，10］中给出了一种空间八面体型VGT的定义和正逆运动学模型，并给出了自由漂浮系统的动力学模型和控制方法，通过物理仿真验证了有效性。文献［11］采用自适应结构的思想研究了航天器搭载多个VGT时的动量管理问题。

在VGT的运动规划问题上，文献［12］给出了一种以可调杆杆长作为控制变量的轨迹跟踪方法，该方法运算高效，但仅针对慢速运动下的直线轨迹有效。文献［13－16］给出了一类角度可调型平面VGT的建模和挠性模态最优辨识方法，并采用序列二次规划算法（Sequential Quadratic Programming，SQP）提出了一种能够有效抑制振动的运动规划方法。文献［17，18］借鉴文献［6－8］的方法，给出了一种离散二状态平面VGT的避障运动规划方法，但不能解决连续杆件的问题。

已有的研究未涉及自由漂浮的杆件连续变化VGT的运动规划问题。本文针对一类由平面VGT作为操作机构的机动过程中的空间组合体，研究了VGT运动规划问题，给出了在单级和多级冗余情形下的规划算法，并通过数学仿真进行了验证。具有较强的工程价值，为空间站舱段机动问题提供了一种解决途径。

1 系统的数学描述

首先给出平面VGT系统的数学描述。如图1所示，系统由基座舱段、负载舱段及N级桁架构成。第k级k＝1，2，…，N（

）桁架包括3根可调长度杆qk，1、qk，2和qk，3，以及下方的固定长度杆wk。第k级与第k＋1级桁架通过固定杆wk＋1连接。基座舱段、负载舱段质量分别为mb和me，绕各自质心的转动惯量分别为Ib和Ie，舱段宽度的一半分别为db和de，长度与固定杆长度相等，基座舱段与桁架共用的固定杆为w1，负载舱段与桁架共用的固定杆为wN＋1。杆件质量集中在端点，质量均为m，wk的左右两端分别为xl，k和xr，k。

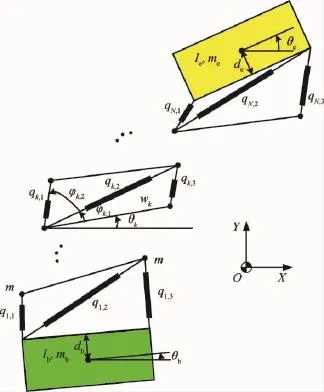
图1 平面VGT系统几何模型示意Fig.1 Geometrical model of planar VGT

建立系统质心坐标系XOY，如图1所示，原点位于系统质心，x轴、y轴分别与惯性系坐标轴平行。每级桁架固定杆wk相对x轴转过的角度为θk。

每根可调杆可以简化为图2所示模型，即端点处的集中质量通过弹簧阻尼相连接。

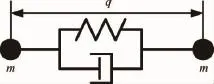
图2 可调长度杆简化模型Fig.2 Simplified model of a varied link

为研究方便，首先给出一些基本假设：

1）仅考虑刚性情形，杆件、基座舱段及负载舱段均为刚体；

2）系统处于自由漂浮状态，忽略轨道运动，忽略重力及其他引力；

3）由于桁架各级通常采用相同的材料及加工方式制成，以便于安装和维护，因而假设各级桁架参数相同，即具有相同的集中质量和相同的固定杆长wk＝w k＝1，2，…，N（

）。

本文研究VGT可调杆的运动规划，实现保证系统始末构型不变，即各可调杆在运动末时刻tf达到与初始时刻相同的长度，同时实现对基座舱段位姿的调节，即使得基座舱段位姿达到期望值。或描述为最优化问题：给定初始时刻t0，初始时刻可调杆长度qo，基座舱段初始位置为，姿态为速度b及角速度，期望末时刻位置和姿态。规划各可调杆的长度函数q（t），t∈［t0，tf］ ，使得在末时刻tf，可调杆长度qf，长度变化率˙qf，基座舱段位置满足：式中：J为优化指标，即实际值与期望值的误差；‖·‖2为向量的2－范数。在此过程中，无外力及外力矩的参与。

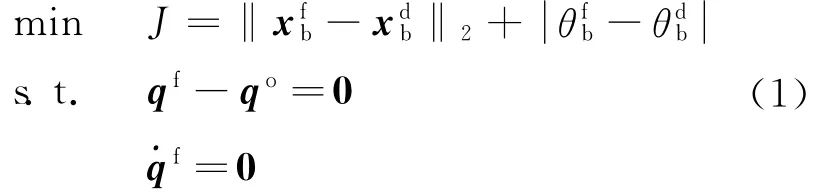
2 组合体运动学模型

根据图1中的几何关系，可计算出第1级桁架左侧顶点位置xl，1和姿态θ1：

利用式（5）递推可得第N＋1根固定杆左顶点位置xl，N＋1及角度θN＋1，从而求得负载舱段质心位置xe和姿态θe：

式中：J为速度Jacobian矩阵，与系统几何参数、惯性参数及可变杆件长度有关；J0为初值矩阵，体现了初始动量的影响。

3 运动规划

在第2节运动学模型的基础上，本节以误差和时间为指标，研究桁架运动规划问题。首先给出单级桁架规划算法，而后在此基础上给出了多级桁架冗余情形下的能量最优规划算法。为避免多根可调杆长度同时变化引起桁架结构的不稳定，故在任意时刻至多仅改变一根可调杆长度。

3.1 单级桁架运动规划算法

由于本文所研究的平面系统，其基座舱段具有3自由度，每级桁架有3根主动调节长度的杆件，因而桁架自由度为3 N。当N＝1时，系统输入输出具有相同的自由度，式（10）中Jacobian矩阵为三阶方阵。本节给出此类单级桁架系统的运动规划算法。为减小运算量，提高运算效率，将选取变化序列与寻找变化时间分开设计。

由于各可调长度杆依次变化长度，则长度变化次序可定义为变化序列S＝s1，s2，…，s2N

｛｝。N级桁架共有3N（）！2个变化序列，每个变化序列包含2 N个有序的非零元素s，每个元素表示一个长度变化的杆件序号，其中，“＋”表示杆件伸长，即˙q≥0，“－”表示杆件压缩，即˙q≤0。

已知：VGT系统桁架为1级，即三根可调杆q1，1、q1，2和q1，3，为记号简单，这里记为q1、q2和q3。基座舱段初始位置为姿态为

求解：规划各可调杆的长度函数q（t）＝［q1（t），q2（t），q3（t）］T，t∈［t0，tf］ 。

算法步骤：

1）各可调长度杆长度变化的加速度绝对值为常值a，单根杆件先压缩，再拉伸恢复原长，压缩与拉伸时间相等。设q1，q2，q3的压缩时间分别为t1，t2，t3，则末时刻：

2）固定变化时间，选取变化序列。首先假设t1＝t2＝t3＝ts，故各杆件杆长变化幅度相同。由于系统角动量守恒，且：

其中使得式（12）指标最小的一组序列；而后采用遗传算法求出满足式（12）的一组运动时间，即得到所求的运动规划。

4 仿真验证

本节对所给出的模型及算法进行数值仿真，以验证其正确性。

首先令t1＝t2＝t3＝0.5s，遍历杆件变化序列，结果如表1所示，选取使得式（11）中的J最小的一组顺序。

仿真结果如图3所示，系统在tf＝3.6s时最终完全复原到初始状态。

4.2 单级桁架规划算法仿真

根据第3.1节给出的算法，采用4.1节中的参数，在无外力及外力矩参与的情形下，设定初

图3 运动学模型仿真结果Fig.3 Results of kinematic model simulation

通过比较表1中数据，选取杆件转动顺序为第14组：S＊＝－2，－1，－3，＋1，＋3，｛＋2｝。在该顺序下，以指标最小化为目标，调用Matlab的遗传算法函数ga来搜索最优解，得到3根杆件的最优变化时间为：t1＝6.997 5s，t2＝7.663 6s，t3＝4.209 3s此时J＝0.879 8，长度变化曲线如图4所示，基座舱段位姿xb（t）及速度˙xb（t）变化如图5所示。

表1 固定时间，不同序列下的误差值Table 1 Results of objective function under different move sequences and same moving time

图4 可调长度杆仿真结果Fig.4 Simulation results of variable links

图5 基座位姿及速度仿真结果Fig.5 Simulation results of states of base body

5 结束语

本文针对由基座舱段、平面VGT、负载舱段组成的组合体在机动过程中，VGT可调杆的长度变化给出了运动规划算法。结果表明：

1）建立了系统几何描述及运动学模型，给出了运动规划目标及约束，将该过程简化为一个最优问题。

2）针对单级桁架连续杆件系统，给出两步寻优的误差最小算法，例如在所给算例中，使得运动轨迹的末时刻位姿误差指标为J＝0.879 8。

3）针对多级桁架冗余系统，给出能量最优运动规划算法。但运算量仍然较大，需要进一步研究减小运算量的方法。

4）本文给出的算法对于以VGT作为操作机构的空间系统的运动具有一定的指导意义。

（

）

［1］ 李广兴，肖余之，卜邵华，等.空间站组装过程姿态控制方案研究［J］.载人航天，2012，18（1）：22－29.LI G X，XIAO Y Z，BU S H，el al.Research on attitude control scheme during space station assembly［J］.Manned Spaceflight，2012，18（1）：22－29（in Chinese）.

［2］ 危清清，王耀兵，唐自新，等.空间站柔性机械臂辅助舱段对接动力学分析［J］.中国空间科学技术，2016，36（3）：24－31.WEI Q Q，WANG Y B，TANG Z X，et al.Analysis on flexible space manipulator system assisted docking of space station［J］.Chinese Space Science and Technology，2016，36（3）：24－31（in Chinese）.

［3］ MIURA K，FURUYA H，SUZUKI K.Variable geometry truss and its application to deployable truss and space crane arm［J］.Acta Astronautica，1985，12（85）：599－607.

［4］ HUANG S，NATORI M C，MIURA K.Motion control of free－floating variable geometry truss，part 1：kinematics［J］.Journal of Guidance，Control，and Dynamics，1996，19（4）：756－763.

［5］ MUROTSU Y，SENDA K，HISAJI K.Optimal configuration control of an intelligent truss structure［J］.Contemporary Physics，1991，42（3）：203.

［6］ CHIRIKJIAN G S，EBERT－UPHOFF I.Numerical convolution on the Euclidean group with applications to workspace generation［J］.IEEE Trans.Robot.Automat.，1998，2（14）：123－136.

［7］ EBERT－UPHOFF I.On the development of discretelyactuated hybrid－serial－parallel manipulators［D］.Baltimore：Johns Hopkins Univ.，1997.

［8］ WANG Y，CHIRIKJIAN G S.Workspace generation of hyper－redundant manipulators as a diffusion process on SE（N）［J］.IEEE Trans.Robot.Automat.，2004，20（3）：399－408.

［9］ MIURA K，FURUYA H.Adaptive structure concept for future space applications［J］.AIAA Journal，1988，26（26）：995－1002.

［10］ HUANG S，NATORI M C，MIURA K.Motion control of free－floating variable geometry truss，part 2：inverse kinematics［J］.Journal of Guidance，Control，and Dynamics，1996，19（4）：764－771.

［11］ HANAHARA K，TADA Y.Motion of variable geometry truss for momentum management in spacecraft［J］.AIAA Journal，2002，40（8）：1673－1676.

［12］ UTKU S，RAMESH A V，DAS S K，et al.Control of a slow－moving space crane as an adaptive structure［J］.AIAA Journal，1991，25（6）：961－967.

［13］ SENBA A，FURUYA H.Identifiability and limitation of self－identification of adaptive structures by variable matrices method［J］.Japan Society of Aeronautical Space Sciences，2004，52（52）：479－486.

［14］ SENBA A，FURUYA H.Implementation algorithms for self－identification of adaptive structures with variable geometric properties［J］.Mechanical Systems ＆Signal Processing，2008，22（1）：1－14.

［15］ SENBA A，FURUYA H.Optimal configuration for the self－identification of a two－dimensional variable geometry truss［J］.Structural ＆Multidisciplinary Optimization，2010，40（1－6）：453－465.

［16］ SENBA A，OKA K，TAKAHAMA M，et al.Vibration

reduction by natural frequency optimization for manipulation of a variable geometry truss［J］.Structural＆Multidisciplinary Optimization，2013，48（5）：939－954.

［17］ MOTAHARI A，ZOHOOR H，KORAYEM M H.A new obstacle avoidance method for discretely actuated hyper－redundant manipulators［J］.Scientia Iranica，2012，19（4）：1081－1091.

［18］ MOTAHARI A，ZOHOOR H，KORAYEM M H.A new motion planning method for discretely actuated hyper－redundant manipulators［J］.Robotica，2017，35（1）：101－118.

（编辑：车晓玲）

Studyon motion planningof variable geometrytruss duringmultibodymaneuvering

DENG Ya，ZHANG Jinjiang＊
Beijing Institute of Control Engineering，Beijing 100190，China

Most of current researches about variable geometry truss（VGT）motion planning only focus on the situation that each bay has single degree of freedom.Motion planning of VGT whose each bay are variable multiple links were investigated.Kinematic model was set up based on the geometrical relationship.Considering momentum conservation of the freefloating system，velocity kinematic model was formulated.A method of designing moving sequence and moving time separately was proposed for motion planning of single bay VGT.Additionally，multi－bay VGT motion planning problem was solved by energy optimum.Simulation results show that the algorithm is effective，and the optimizing index is 0.879 8.The method has practical benefits to the space operation system with VGT.

V448.2

A

10.16708／j.cnki.1000－758X.2017.0045

2016－11－09；

2017－03－27；录用日期：2017－06－29；网络出版时间：2017－08－11 13：21：16

http：∥kns.cnki.net／kcms／detail／11.1859.V.20170811.1321.009.html

邓雅（1988－），女，博士研究生，dengyahit＠163.com，研究方向为航天器控制

＊通讯作者：张锦江（1973－），男，博士，研究员，ewindzjj＠163.com，研究方向为航天器控制、制导与仿真

邓雅，张锦江.组合体机动中可变形桁架运动规划研究［J］.中国空间科学技术，2017，37（4）：10－17.

DENG Y，ZHANG J J.Study on motion planning of variable geometry truss during multibody maneuvering［J］.Chinese Space Science and Technology，2017，37（4）：10－17（in Chinese）.