挠性充液航天器超近程逼近段动力学建模与控制

王首喆，刘华清，张庆展，靳永强，＊，盛英华.上海宇航系统工程研究所，上海009.上海卫星工程研究所，上海009

挠性充液航天器超近程逼近段动力学建模与控制

王首喆1，刘华清2，张庆展1，靳永强1，＊，盛英华1
1.上海宇航系统工程研究所，上海201109
2.上海卫星工程研究所，上海201109

超近程逼近过程中，服务航天器为刚柔液耦合的复杂系统，单摆等液体晃动模型不再适用，对这种工况下的航天器进行了动力学建模与控制的研究。采用虚功率原理推导了一种新的适用于三轴推力作用下的液体晃动等效模型，通过引入相对位置导引矢量与相对位置误差矢量，建立了相对轨道误差动力学模型，结合相对姿态动力学模型，得到超近程逼近段的刚柔液耦合的相对轨道姿态动力学模型。针对模型存在的不确定性和未知干扰，设计了基于滑模估计器的相对姿轨耦合控制律。通过数学仿真验证了控制律的有效性，仿真中的晃动结果与Flow－3D结果能够吻合，验证了晃动模型的合理性。

在轨服务；超近程逼近；轨迹导引；刚柔液耦合；相对姿轨耦合；滑模估计器

在轨服务是指服务航天器携带设备装置与目标航天器发生相互作用的过程，进而达到服务的目的。服务航天器一般安装有大型挠性附件（如天线和太阳翼）、携带较多的液体推进剂，是一个刚柔液耦合非线性系统。这种航天器用于推进剂补加、模块更换、在轨维修、碎片捕获清除等任务。超近程逼近是执行以上操作的关键步骤，需控制服务航天器使其沿目标被动对接口方向逼近，且主动对接口沿逼近方向指向被动对接口［1］，使得服务航天器的相对位置与姿态也存在耦合。与轨道转移的情况不同，超近程逼近过程中不存在某一方向的恒定推力，需要在服务航天器三轴方向频繁喷气来实施相对姿态和轨道的控制，贮箱内推进剂的液体表面张力作用得到凸显［2］，常规的液体晃动单摆模型不再适用。因此，服务航天器在超近程逼近段的动力学复杂，存在较多不确定性，加上未知干扰的作用，建模难度大，对控制的鲁棒性要求高。

针对以上问题，文献［3］对编队飞行中的相对姿轨耦合动力学建模与控制模型进行了研究；文献［4］建立了刚体的姿轨耦合动力学模型，并设计了相应的控制律；文献［5］根据期望编队点推导出相对轨道误差动力学模型；文献［6］将Twisting算法与线性补偿项相结合，设计了相对位姿耦合控制律。上述文献建立的均是刚体模型，未考虑挠性与液体晃动的影响。文献［7］针对航天器挠性结构持续振动问题，提出一种基于模糊控制原理的自抗扰控制方法；文献［8］针对刚柔耦合姿态动力学模型，提出了基于直接自适应的姿态稳定控制律；文献［9］对在恒定推力作用下的充液航天器建立了等效单摆模型，并设计了一种滑模观测器来估计液体的晃动角。上述文献考虑了挠性或液体晃动对姿态的影响，未考虑轨道受到的影响。文献［10］对自动转移飞行器的液体燃料建立晃动等效力学模型，通过数值仿真得到相关参数并进行了对比，未对与姿轨动力学结合的情况进行分析。

文章针对上述问题，采用一种新的适用于三轴推力作用下的液体晃动等效力学模型，建立了完整的刚柔液耦合姿态轨道动力学模型，将复杂的相对轨道跟踪控制问题转化为简单的调节器设计问题，最后设计了基于滑模估计器的相对姿轨耦合控制律对模型进行仿真。

1 建立数学模型

1.1 坐标系定义

文章涉及的坐标系有：1）J2000地心惯性坐标系Oi－XiYiZi；2）相对轨道坐标系Ot－XtYtZt；3）质心轨道坐标系Oo－XoYoZo；4）服务航天器本体坐标系Ob－XbYbZb与目标航天器本体坐标系Od－XdYdZd，以上坐标系与常规定义相同；5）服务航天器对接坐标系Oq－XqYqZq与目标航天器对接坐标系Op－XpYpZp，根据对接装置的具体安装情况定义，文章假设对接坐标系三轴方向与本体坐标系三轴方向平行；6）贮箱固连坐标系Oz－XzYzZz三轴与体坐标系三轴平行，质心Oz位于贮箱球心。

1.2 液体晃动等效模型

超近程逼近过程中，由于没有恒定方向的推力作用，航天器贮箱中的液体无法沉底，而是包裹在贮箱壁面上，内部产生空腔，在三轴推力作用下作小幅晃动。如图1所示，假设贮箱为球形，将贮箱内的液体分为静止质量和晃动质量，用固连在球心的具有惯量的质量块表示静止质量，晃动质量视为质点，与4个在贮箱内部均匀分布且与贮箱相连的弹簧阻尼器相连，平衡状态下晃动质量位于球心［2］。

图1 液体晃动等效模型Fig.1 Spring－mass equivalent mechanical model

模型中，4个弹簧阻尼器的刚度和阻尼系数完全相同，假设4个弹簧阻尼器的总体刚度是K，总体阻尼系数是ξ，液体静止质量为m0，晃动质量为mh，静止质量块的质点相对服务航天器本体坐标系原点的位置矢量为r0，晃动质点相对平衡点即球心的位置记为rh，晃动质点相对服务航天器本体坐标系原点的位置矢量为r0h＝r0＋rh，由于小幅振动，将rh视为小量。服务航天器质心在惯性系下的位置矢量为rs。

利用虚功率原理建立模型的动力学方程：

式中：δPIh，δPKh，δPdh，δPgh，δPg0，δPI0分别为晃动质量的惯性力虚功率、弹性力虚功率、阻尼力虚功率、地球引力虚功率及静止质量的地球引力虚功率、惯性力虚功率；δPa为晃动模型受到的外力虚功率。

通过速度变分的形式表示各个虚功率，分别得到液体的平动方程、转动方程和振动方程为：

式中：mt为服务航天器的干质量；us和ds分别为控制加速度和外力扰动速度；k为太阳翼板个数；Jt为服务航天器干重的转动惯量；Tc、Td为服务航天器受到的控制力矩和干扰力矩；Mj为航天器翼板的耦合矩阵；ηj为翼板的模态坐标；ζj为翼板的挠性模态振动阻尼比；Ωj为翼板的挠性模态振动频率；BTj和BRj分别为挠性附件的平动及转动耦合系数矩阵；a为航天器在非惯性外力作用下的加速度。

将式（2）与式（5）结合，（Jh＋J0）·˙ωb与Jt˙ωb合并为J˙ωb，静矩相关项合并后为零，Sh×｛ωb×［ωb×（r0＋rh） ］｝可转换为ωb×（Js·ωb） ，可以与ωb×（J0·ωb）、ωb× Jtωb合并为ωb×（J·ωb），J为服务航天器总转动惯量。记mhi（r0＋rhi）×（¨rhi＋2ωb×˙rhi）为T′hi，服务航天器姿态动力学方程为：

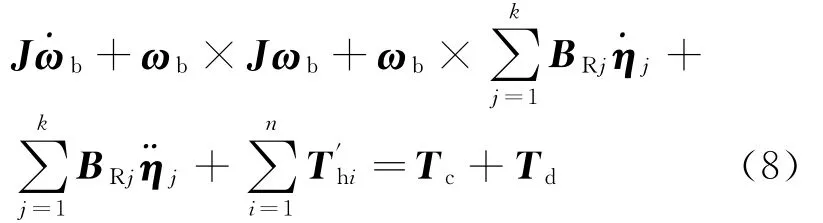
1.3 相对轨道动力学模型

图2为对接装置之间相对位置关系，其中，rd为目标航天器的质心位置矢量，r1，r2分别为目标航天器、服务航天器对接装置的安装矢量；~l为两航天器对接装置之间的位置导引矢量，

l为~l对应的两航天器质心间相对位置路径，

rds为两航天器质心间的实际相对位置，Δr为l与rds间的偏差。存在：

~l＝l－r1＋r2， rds＝l＋Δr（9）

结合式（3），服务航天器与目标航天器的相对轨道动力学方程：

式中：ud、dd分别为目标航天器受到的控制力加速度和扰动外力加速度。

式：ωti＿t为Ot－XtYtZt相对Oi－XiYiZi的角速度在Ot－XtYtZt下的表示。

作用在组合体的控制力产生的加速度在Ob－XbYbZb下表示为：

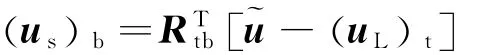
对位置导引矢量l~进行设计。如图3所示，S型速度曲线能对加速度的变化率进行控制，加速度曲线连续，在速度衔接处可实现平稳过渡，是一种能限制振动的速度控制方法［13］，所以选用S型速度曲线对l~进行设计。逼近过程中，根据航天器推力器配置情况，对加速度进行限幅，使其满足为推力器能提供的最大推力，m为航天器总质量。

图3 S型速度曲线示意Fig.3 S－shaped velocity curve

1.4 相对姿态运动学与动力学模型

采用四元数作为姿态描述参数，结合式

2 相对姿轨耦合控制律设计

由于姿态四元数各元素平方和为1，姿态

控制时只对四元数矢量部分qe进行控制，有

由于服务航天器的挠性附件、液体晃动及受到的干扰难以测量或估计，故Δ项难以确定。定义e＝x－xd为系统状态误差，xd＝0、为期望状态，设计的控制律要求使x→x即

针对未知干扰与系统的不确定性，设计基于滑模估计器的相对姿轨耦合控制律。在传统滑模面s＝˙e＋ke的基础上，增加辅助滑模变量η，设计滑模面sd＝s＋η，其中：

针对滑模控制中符号函数高速切换引起的震颤问题，采用饱和函数代替的方法进行处理。

3 仿真

3.1 仿真条件

对服务航天器向目标的逼近过程进行仿真，采用直线逼近策略。初始时刻，目标航天器为圆轨道，轨道半径rd＝6 778 137m，轨道倾角id＝51.6°，升交点赤经Ωd＝0°，近地点幅角ωd＝0°，姿态为对地定向，Od－XdYdZd相对Oo－XoYoZo初始欧拉角均为0°。在Ot－XtYtZt下服务航天器相对目标的位置矢量为［0.5；150.5；0.5］，各轴相对速度0.1m／s，Ob－XbYbZb相对Oo－XoYoZo初始欧拉角［－1° 1.5° 0.5°］，对地定向。S型速度规划导引律设计加加速度0.000 01m／s3、最大加速度0.001m／s2、最大速度0.2m／s。两航天器对接口距各自质心距离均为1.5m，当服务航天器对接口逼近至距离目标航天器对接口1m（即质心相距4m）时设置停泊点。

服务航天器相关参数有：转动惯量J＝diag（［3 645，4 448，444 8］）kg·m2，整星（含太阳翼板和推进剂）质量m为3 500kg，推进剂质量1 797kg，其中氧化剂四氧化二氮1 120kg，燃料MMH 677kg，航天器三轴可施加最大推力50N，最大力矩75N·m。

服务航天器挠性附件的模态频率矩阵Λ＝diag（0.31 0.83 1.33 1.56 4.66）Hz，阻尼比矩阵ζ＝diag（0.05 0.05 0.05 0.05 0.05）。

液体晃动模型相关参数：1）氧化剂N2O4静止质量711kg，晃动质量409kg，充液比为86%，弹簧阻尼器刚度系数353.455N／m，阻尼系数20.20；2）燃烧剂甲基肼静止质量430kg，晃动质量247kg，充液比为86%，弹簧阻尼器刚度系数42.880 0N／m，阻尼系数67.086 0。控制律相关参数：k＝diag（0.5 0.5 0.5 0.3 0.3 0.3），kr＝diag（0.05 0.05 0.05 0.01 0.01 0.01），

kd＝0.15，控制时将转动惯量J作拉偏25%的

处理，并考虑干扰的影响。

3.2 仿真结果及分析

图4为相对姿态跟踪误差曲线，约50s后服务航天器与目标的姿态同步，姿态角跟踪精度5× 10－5（°），姿态角速度跟踪精度2×10－9（°）／s。图5为相对轨迹变化曲线，在S型速度曲线导引律下，服务航天器在1 090s时到达指定停泊点，且服务航天器对接口距目标对接口保持1m的停泊距离；在360～790s，服务航天器以最大相对速度0.2m／s接近目标。图6为相对轨迹跟踪误差曲线，约45s后服务航天器位置、速度与规划的位置、速度同步，位置跟踪精度1×10－4m，速度跟踪精度2×10－6m／s。图7给出了挠性翼板前三阶模态的坐标值，稳态时坐标均小于1×10－7。图8以甲基肼为例，将液体晃动等效模型与Flow－3D结果进行对比，图7（a）～（c）为力对比，图7（d）～（f）为力矩对比，除一些明显毛刺外，等效模型能较好地预测晃动力与力矩的幅值。图9为控制力与控制力矩曲线，由于初始姿态、位置误差的存在，使得控制力与力矩在开始阶段较大，由于服务航天器沿体坐标x轴逼近目标，所以x轴方向控制力与S型速度规划的加速度变化相匹配。

仿真结果表明，所建的刚柔液耦合动力学模型是正确的，设计的控制律能够使航天器沿着预定轨迹，按照设计的S型速度曲线运动规律完成对目标的逼近，具有较高的控制精度。晃动等效力学模型能够与Flow－3D的结果较好地吻合，即能够较好地预测超近程逼近过程中液体晃动的状态。

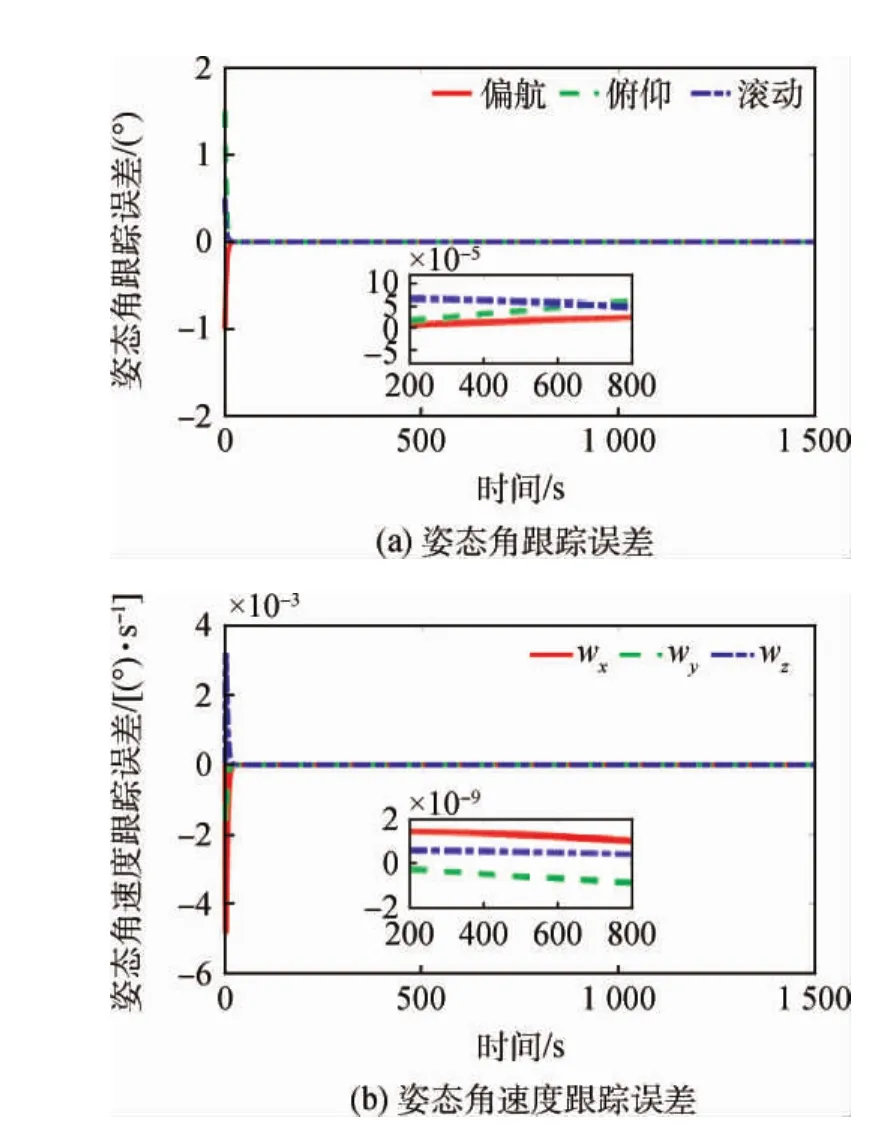
图4 相对姿态跟踪误差曲线Fig.4 Curve of relative attitude tracking errors

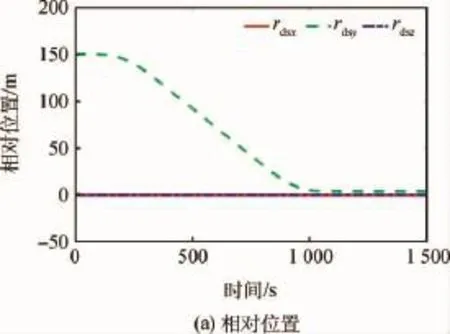
图5 服务航天器与目标间相对轨迹曲线Fig.5 Curve of relative trajectorybetween servicing spacecraft and object

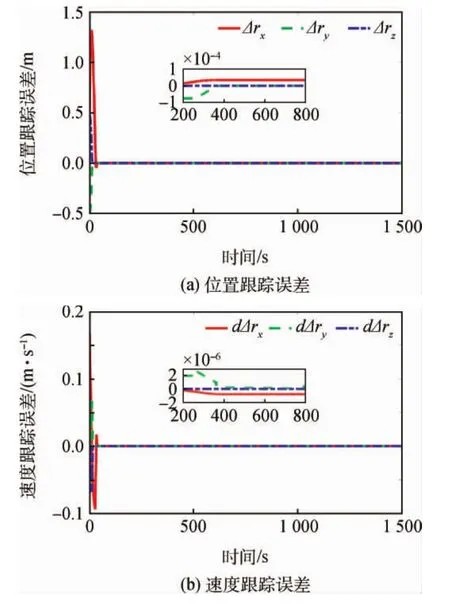
图6 相对轨迹跟踪误差曲线Fig.6 Curve of relative trajectory tracking errors

图7 挠性模态变量随时间收敛曲线Fig.7 Curve of flexible modal

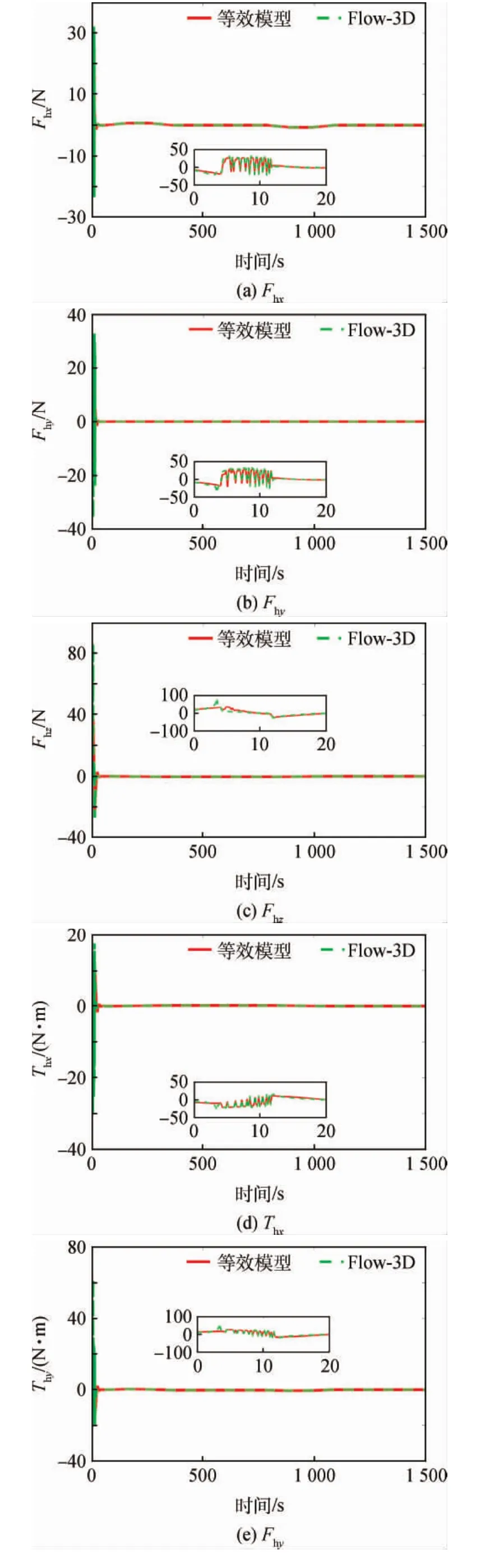
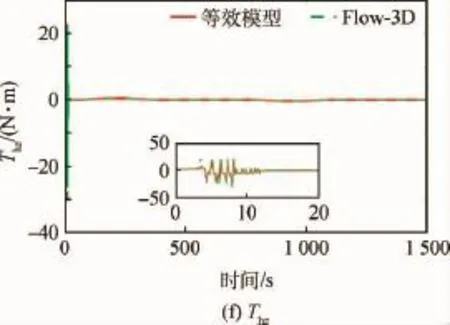
图8 晃动作用对比（等效模型vs.Flow－3d）Fig.8 Slosh force comparison

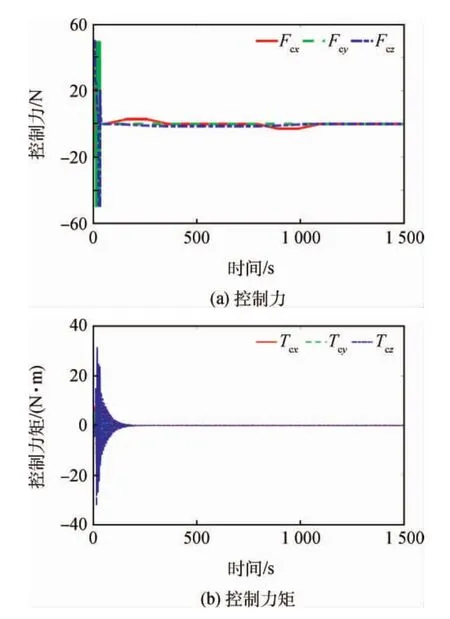
图9 控制力与控制力矩Fig.9 Control force and control torque

4 结束语

文章对服务航天器与目标交会对接的超近程逼近段动力学建模与控制问题进行了研究。动力学建模中，考虑逼近过程中液体晃动的特殊性，采用新的液体晃动等效力学模型，给出了刚柔液耦合的相对动力学模型。考虑模型的不确定性与未知干扰，设计了基于滑模估计器的相对姿轨耦合控制律并进行了稳定性分析。仿真结果表明控制律的控制性能较好，具有一定的鲁棒性。通过将仿真中的晃动结果与在相同激励下的Flow－3D结果进行对比，表明建立的晃动模型符合超近程逼近段液体晃动的规律，具有一定的适用性。文章的研究对在轨服务技术的发展提供了一定的参考。

（

）

［1］ 张庆展，靳永强，康志宇，等.服务航天器超近程逼近目标的相对姿轨耦合控制［J］.系统工程与电子技术，2015，37（1）：141－147.ZHANG Q Z，JIN Y Q，KANG Z Y，et al.Coupled control of relative position and attitude for servicing spacecraft approaching the target in close proximity［J］.Systems Engineering and Electronics，2015，37（1）：141－147（in Chinese）.

［2］ 王天舒，苗楠，李俊峰.航天器交会对接中液体燃料晃动等效模型研究［J］.空间控制技术与应用，2015，41（3）：1－7.WANG T S，MIAO N，LI J F.Liquid sloshing equivalent mechanical model during rendezvous and docking［J］.Aerospace Control and Application，2015，41（3）：1－7（in Chinese）.

［3］ PAN H Z，KAPILA V.Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics［C］∥Proceedings of the IEEE Conference on Decision and Control，Orlando，FL.，USA，4－7December，2001，IEEE Xplore：2057－2062.

［4］ 卢伟，耿云海，陈雪芹，等.在轨服务航天器对目标的相对位置和姿态耦合控制［J］.航空学报，2011，32（5）：857－865.LU W，GENG Y H，CHEN X Q，et al.Coupled control of relative position and attitude for on－orbit servicing spacecraft with respect to target［J］.Acta Aeronautica et Astronautica Sinica，2011，32（5）：857－865（in Chinese）.

［5］ XING G Q，PARVEZ S A.Implementation of autonomous GPS guidance and control for the spacecraft formation flying［J］.Frontier Science，2008，2（5）：56－66.

［6］ 耿云海，陈炳龙，梁海朝.改进Twisting算法的相对位姿耦合控制［J］.哈尔滨工业大学学报，2015，47（11）：6－14.GENG Y H，CHEN B L，LIANG H C.Relative position and attitude coupled control based on modified twisting algorithm［J］.Journal of Harbin Institute of Technology，2015，47（11）：6－14（in Chinese）.

［7］ 刘福才，陈鑫，贾亚飞，等.模糊自抗扰控制器在挠性航天器振动抑制中的应用［J］.振动与冲击，2015（9）：9－14.LIU F C，CHEN X，JIA Y F，et al.Application of fuzzy auto disturbance rejection controller in flexible spacecraft vibration suppression［J］.Journal of Vibration and Shock，2015（9）：9－14（in Chinese）.

［8］ 刘敏，徐世杰，韩潮.基于直接自适应的挠性航天器姿态稳定控制［J］.中国空间科学技术，2012，32（4）：1－7.LIU M，XU S J，HAN C.Flexible spacecraft attitude stabilization control based on direct adaptive algorithm［J］.Chinese Space Science and Technology，2012，32（4）：1－7（in Chinese）.

［9］ 史星宇，齐瑞云.基于滑模观测器的充液航天器姿态控制［J］.航天控制，2015，33（4）：11－16.SHI X Y，QI R Y.Attitude control of spacecraft with fuel slosh based on sliding mode observer［J］.Aerospace Control，2015，33（4）：11－16（in Chinese）.

［10］ BAYLE O，L′HULLIER V，GANET M，et al.Influence of the ATV propellant sloshing on the GNC performance［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Washington D.C.：AIAA，2002.

［11］ 屠善澄.卫星姿态动力学与控制［M］.北京：宇航出版社，2001.TU S C.Satellite attitude dynamics and control［M］.Beijing：Aerospace Publishing house，2001（in Chinese）.

［12］ 宋斌，颜根廷，李波，等.基于自抗扰技术的挠性航天器高精度指向控制［J］.上海航天，2014，31（2）：1－7.SONG B，YAN G T，LI B，et al.Active disturbance rejection control for flexible spacecraft high－accuracy attitude pointing［J］.Aerospace Shanghai，2014，31（2）：1－7（in Chinese）.

［13］ 刘蕾，曾辉，柳贺，等.六自由度机器人S型曲线速度规划［J］.计算技术与自动化，2015（2）：42－45.LIU L，ZENG H，LIU H，et al.S－curve velocity planning for 6－DOF robot［J］.Computing Technology and Automation，2015（2）：42－45（in Chinese）.

［14］ BROWN M D J.Finite reaching time continuous sliding mode control with enhanced robustness［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Denver，CO，U.S.A.，14－17August，2000：1－12.

（编辑：车晓玲）

Modelingand control for a liquid－filled spacecraft with flexible appendages in close proximity

WANG Shouzhe1，LIU Huaqing2，ZHANG Qingzhan1，JIN Yongqiang1，＊，SHENG Yinghua1
1.Aerospace System Engineering Shanghai，Shanghai 201109，China
2.Shanghai Institute of Satellite Engineering，Shanghai 201109，China

In close proximity，the servicing spacecraft is a complex system with rigidflexible－liquid coupled，and the liquid sloshing model，such as pendulum，isn′t applicable.The dynamics modeling and control of this spacecraft were studied.Firstly，a kind of new liquid sloshing equivalent mechanical model was derived by virtual work principle，and it could be applied to the situation of tri－axial thrust.Secondly，a relative position guidance vector and a relative position error vector were defined，and a relative position error dynamics model was derived.Thirdly，combining the relative position error dynamics with the relative attitudedynamics，a coupled relative attitude－orbit dynamics model was established，which was suitable for the process of close proximity in rendezvous and docking.The model was also rigid－flexibility－liquid coupled.Finally，a control law based on the slide－mode－control was designed to estimate the unknown but bounded disturbances，system uncertainties and measurement noise.The effectiveness of the control law was validated by numerical simulation.The results of the sloshing in the simulation agree well with the Flow－3Dresults，which indicates that the liquid sloshing equivalent mechanical model is reasonable.

on－orbit servicing；close proximity；trajectory guidance；rigid－flexible－liquid coupled；relative attitude－orbit coupled；sliding mode estimator

V412.4

A

10.16708／j.cnki.1000－758X.2017.0041

2016－08－23；

2017－01－06；录用日期：2017－06－29；网络出版时间：2017－08－11 10：27：17

http：∥kns.cnki.net／kcms／detail／11.1859.V.20170811.1027.003.html

上海市科学技术委员会资助项目（14XD1423400）

王首喆（1992－），男，硕士研究生，wszlssb＠163.com，研究方向为飞行器总体设计

＊通讯作者：靳永强（1981－），男，高级工程师，jyq413＠bit.edu.cn，研究方向为飞行器总体设计

王首喆，刘华清，张庆展，等.挠性充液航天器超近程逼近段动力学建模与控制［J］.中国空间科学技术，2017，37（4）：

1－9.WANG S Z，LIU H Q，ZHANG Q Z，et al.Modeling and control for a liquid－filled spacecraft with flexible appendages in close proximity［J］.Chinese Space Science and Technology，2017，37（4）：1－9（in Chinese）.