液体-液体相变与反常特性∗

李任重 武振伟 徐莉梅2)†

1)(北京大学物理学院,国际量子材料中心,北京 100871)

2)(量子物质科学协同创新中心,北京 100871)

液体-液体相变与反常特性∗

李任重1)武振伟1)徐莉梅1)2)†

1)(北京大学物理学院,国际量子材料中心,北京 100871)

2)(量子物质科学协同创新中心,北京 100871)

(2017年6月26日收到;2017年8月16日收到修改稿)

绝大多数物质的液态密度随温度降低而增大,即常见的热胀冷缩现象.但存在一类物质,如水及第四主族的硅、锗等,其液态密度在一定温度范围内随温度的升高而增大,即密度反常现象.此外,该类物质还存在动力学反常(密度越大粒子运动越快)、热力学反常(热力学量的涨落随温度降低而升高)等其他反常特性.这类材料的化学性质千差万别,但却具有相似的物理反常特性.进一步的理论研究发现部分材料具有两种液态,即高密度液态和低密度液态,两者之间存在一级相变.因此,反常特性与液体-液体相变是否有直接关联是一个值得深入研究的课题.本文主要介绍了具有液体-液体相变的一类材料及其反常特性,包括高温高压下氢的液体-液体相变及其超临界现象,镓的反常特性及其与液体-液体相变的关联等.

液体-液体相变,临界现象,反常特性,Widom线

1 引 言

热胀冷缩是我们日常生活中的常见现象,绝大多数物质在温度升高时体积膨胀,温度降低时体积缩小,即固体的密度一般大于液体的密度.但是水的液态密度在一定温度范围内会随温度的升高而增加,在4°C下密度最大,称为密度反常现象[1,2]. 例如,冬天时会看到冰浮在水的表面上说明固态水的密度小于液态水.此外,水还表现出诸多热力学反常特性[1−10],例如等温压缩系数κT(≡〈(δV)2〉/(V kBT))、 等压比热容Cp(≡〈(δS)2〉/(NkB))及热膨胀系数αP(≡〈(δSδV)〉/(V kBT))[2,3]等与体积涨落(δV)和熵涨落(δS)相关的热力学参数随温度降低而呈现与大多数物质不同的反常趋势.对大多数液体而言,与热力学量相关的涨落会随温度降低而减小[2,4],即等温压缩系数(体积的涨落)、等压比热容(熵的涨落)、热膨胀系数(体积和熵的涨落)等随温度降低而减小,但水的这些热力学量在一定温度区间内却随着温度降低有明显增加的反常现象.

为了解释水的反常现象,人们提出许多理论[11−14],其中液体-液体相变理论是目前理论与实验上广为接受的理论之一.液体-液体相变理论是指:液体存在高密度(HDL)和低密度(LDL)两种液态,二者之间存在一级相变,即液体-液体相变,其两相共存线的终点是液体-液体临界点.该理论指出临界点附近的临界涨落可能是液体诸多反常现象的根源.因此,能否实验探测到该临界点是实验对此理论的终极验证.但是在很多情况下,理论预测的液体-液体临界点或处在结晶不可避免的相区间[14−16],或处在高温高压相区间,而目前的实验技术无法或难以直接探测到[17,18].以水为例,基于不同模型(如ST2[19,20],SPC/E[21],TIP5P[22,23]等)的理论与计算研究表明水中存在着两种液体,但理论预测的液体-液体相变在水的深过冷区间(136—206 K)[24,25]远低于水的自发成核温度(常压下232 K),因此实验上很难直接验证水中存在液体-液体相变.

目前,在理论与计算研究中预言存在两种液态的体系有很多,单质材料如碳[26]、氮[27,28]、氢[29]、硅[30,31]、磷[32]、镓[33]、锗[34]、硒[35]、硫[35]、碘[35]、铈[36]等,化合物材料除了水[14]还有二氧化硅[16],Y2O3-Al2O3[37]、铝铈合金[37−39]等.目前为止,仅Y2O3-Al2O3[37]和磷[32]的液体-液体相变在实验上被证实.如图1所示,上述单质材料在元素周期表中的位置没有一致的规律,它们分布在第I,III,IV,V,VI,VII主族以及镧系等,具有非常不同的电子结构特点和化学性质.如果再考虑到存在液体-液体相变的化合物,涉及的元素会更多,电子结构层面的规律更不明显.因此,在以上化学性质差异巨大但被预言具有液体－液体相变的材料中找到某些共性是一个重要的前沿问题.

进一步的理论研究发现大多数被预测存在液体-液体相变的材料都具有类似于水的反常现象,如负熔解曲线或密度反常.一般情况下,固态密度大于液态密度,根据克拉伯龙方程

其中P是压强,L为相变潜热.从固态到液态,ΔS＞ 0,ΔV ＞0,因此固体-液体两相共存线在PT相图中斜率为正.反之,如果两相共存线为负值,

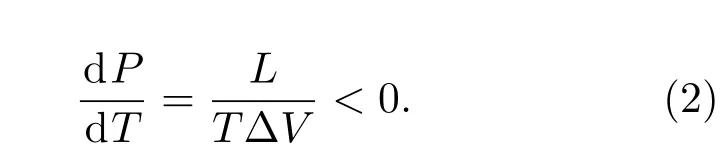
由于相变潜热L和温度恒大于零,说明ΔV＜0,体积随温度增加而降低,即密度反常现象.磷、镓、硅、氮(图2(a))、氢(图2(b))、铈 (图2(c))等材料的相图都显示其固体-液体两相共存线在某一压强温度区间内斜率为负,因此上述物质与水类似,都具有密度反常现象.

图1 元素周期表中用蓝色标注的元素是目前实验或者计算模拟中被认为存在液体-液体相变的单质材料Fig.1.The elements in the periodic table labeled by blue boxes are the elemental materials which exist the liquid-liquid phase transition(LLPT)in experimental or computational studies.

图2 多种材料的相图,分别为(a)氮[27],(b)氢[29],(c)铈[36]Fig.2.The phase diagrams of various materials,such as(a)nitrogen[27],(b)hydrogen[29],(c)cerium[36].

图3 动力学反常特性 (a)水的动力学反常[10];(b)硅的动力学反常[30]Fig.3.Dynamic anomaly:(a)Dynamic anomaly of water[10];(b)dynamic anomaly of silicon[30].

除密度反常之外,相关材料中还发现了动力学反常.一般情况下,体系的扩散系数会随着密度的增加而单调地减少.但存在一类材料,如水[10]、硅[30,31]、镓[40]、二氧化硅[41]等,其动力学扩散系数在某些相区间随密度增加而增大,并存在极大值.如图3所示,高温下水和硅的扩散行为符合一般规律,但在低温时它们却存在扩散系数随密度增加而增大的现象,表明这类材料具有动力学反常特性.

可以发现这类被预言存在液体-液体相变的材料大都具有与水类似的反常特性,包括密度、热力学、动力学反常等.因此,在宏观物理性质上展现出的液体-液体相变或许与反常特性密切关联.本文主要以单质氢和镓为例,具体介绍液体-液体相变及其与反常特性之间的关联.

2 高温高压下氢的液体-液体相变

2.1 氢的液体-液体相变

高温高压下液态氢性质的研究一直受到广泛关注[17,29,42−48].1996年,Weir等[42]将液氢样品放在蓝宝石顶砧之间,让冲击波在两片蓝宝石间来回反射形成多次冲击可使压强最高达到180 GPa.他们发现在温度3000 K附近,140 GPa的液态氢会发生从半导体变为导体的连续相变,其电导率增加4个数量级.2007年,Fortov等[43]运用柱面激波汇聚技术压缩氘样品,发现在压强为140 GPa时,液氘的电导率和密度都发生了突变,其中电导率增加了5个量级,密度增加了20%.不过,由于电导和密度在同一密度压强区内发生不连续变化,并具有一级相变的特征,说明氘的金属化相变区和液体-液体相变区重合,这与Weir等认为的连续金属化过程相反.Fortov等的实验由于使用多次回弹反射技术,使得温度误差很大,初步估计液体-液体相变区温度在3000—8000 K之间.因此,在实验上想要精准测量高温高压下液态氢的性质和行为是极其困难的.迄今为止,还没有公认的实验证明液态氢存在液体-液体相变的证据.

近年来,针对液态氢是否存在一级液体-液体相变,主要有两种观点:一种认为液态氢不存在一级相变,液态氢的金属化过程是连续的[44,45];另一种认为液态氢存在一级相变,且金属化相变区与液体-液体相变区重合[17,29,46−48].2006年,Ceperly等[44]应用量子蒙特卡罗方法研究高温高压下的氢,并没有在液态氢中发现存在一级液体-液体相变的证据.2008年,Holst等[45]利用第一性原理分子动力学模拟也同样得出了液态氢的金属化过程是连续变化的结论.但是也有越来越多的研究显示液态氢中存在一级液体-液体相变.例如,2003年,Scandolo等[46]在第一性原理分子动力学模拟中发现液态氢存在一级相变.他们研究了熔解曲线以上75—175 GPa范围内氢的性质,给出了液态氢的相变温度和压强,T=1500 K,P=125 GPa.Bonev等[47]在2004年通过第一性原理分子动力学模拟发现液态氘中也存在液体-液体相变.Ceperly实验小组[17,29,48]自2010年起先后利用第一性原理分子动力学模拟、耦合电子离子蒙特卡罗方法、路径积分分子动力学模拟等都证实液态氢分子解离为氢原子的过程与氢的金属化过程同时发生,并伴随着密度、电导率、径向分布函数的突变,从而说明这一过程是液态分子氢到液态原子氢的一级相变过程.

2.2 液态氢的超临界现象

如上所述,理论预测氢的液体-液体相变在超高压相区间(100 GPa以上)[29],实验难以直接测量.这也是目前还没有高压下液态氢存在液体-液体相变及临界点直接实验验证的原因.最近的研究发现液体-液体相变的实验验证可以通过研究临界点以外的超临界现象来实现[49−52].超临界现象是指体系的状态参量在超临界区沿着等压线(或等温线)单调地连续变化,但是其响应函数对温度(或压强)的导数会出现极大值,且越接近临界点极值越大;同时,这些响应函数极值线的渐近线被称为Widom线,且Widom线的终点为液体-液体相变临界点[49−52].这一理论为实验直接验证液态氢存在液体-液体相变提供了可能,即从实验容易测量的低压高温相区间通过探测超临界现象来追踪临界点.

基于密度泛函理论,李任重等[18]利用第一性原理分子动力学模拟研究了高温高压下单质氢的液体-液体相变及其超临界现象,特别是对温度2000—2500 K下氢的相区间开展了研究.他们关注的问题是:1)高压液态氢是否存在液体-液体相变及反常现象?2)是否可以通过研究氢的低压高温区发现超临界现象的存在,进而通过定位Widom线的终点探测氢的液体-液体相变临界点?

他们发现体系的体积(图4(a))和电导(图4(b))在2200 K及以下随着压强的变化出现明显的跃变,而在2300 K及以上连续变化,说明2200 K及以下发生液体-液体一级相变,而体系在2300 K及以上对应的是一种连续的变化.对局域结构参量 f(定义为氢原子占体系氢总量的比例,即氢分子的解离程度)分析也给出同样的结论(图4(c)).此外,李任重等[18]还计算了体系热力学、电导率和结构参量的响应函数,即等温压缩系数κT=、电导率对压强的导数dσ/dP,以及局域结构参量对压强的导数df/dP.如图4(d)—图4(f)所示,响应函数有三个特点:1)沿等温线,每个响应函数都有一个极大值,且峰值随着温度降低逐渐往高压方向移动;2)每一个响应函数的峰值幅度都随温度降低而增加,并在接近2300 K时趋于发散;3)对于不同的响应函数,它们的极大值所对应的压强不同.需要特别指出的是这种压强的差异随温度的降低而逐渐缩小,如图5所示响应函数极值线在P-T相图中会逐渐汇聚成一条线,即Widom线.由于宏观量在2200 K及以下出现不连续的跃变,说明在2200 K及以下体系存在一级相变;而根据超临界现象理论[49,50],Widom线终止于液体-液体相变临界点,由此他们预测氢的液体-液体相变临界点位于(2300 K,77 GPa)和(2200 K,81 GPa)之间.

图4 氢的热力学量和结构参量及其响应函数随压强的变化 (a)体积,(b)电导率,(c)局域结构(氢分子的解离程度)在不同温度下随压强变化的趋势;(d)等温压缩系数κT,(e)直流电导率关于压强的导数dσ/dP,(f)局域结构关于压强的导数df/dP沿着等温线的变化示意图[18]Fig.4.Thermodynamic properties and their response functions of hydrogen as function of pressure:properties such as volume(a),conductivity(b)and fraction of molecular hydrogen population(c)as a function of pressure,and response functions with respect to pressure along constant temperatures,such as isothermal compressibility κT(d),the derivative of the electronic conductivity dσ/dP(e),and the change in hydrogen molecular dissociation coefficient df/dP(f)[18].

图5 液态氢的P-T相图 如插图所示,不同响应函数的极值线κT(max)(空心圆),dσ/dP(max)(空心方块),df/dP(max)(空心菱形)轨迹不同,这些轨迹的差异随着温度逐渐趋向于液体-液体相变临界点(红色实心圆)而逐渐变小,直至消失;在临界点以下响应函数在通过一级液体-液体相变点(黑色实心方块)时会发散[18]Fig.5.The P-T phase diagraMof liquid hydrogen.As shown in the inset,the loci of di ff erent response function maxima, κT(max)(open circle),dσ/dP(max)(open square),df/dP(max)(open diamond),are different.Such di ff erences become smaller and disappear as the liquid-liquid critical point( fi lled circle)is approached froMthe supercritical region.Below the LLCP,the response functions diverge as the fi rst-order LLPT line( fi lled square)is crossed[18].

3 液态镓的液体-液体相变与反常现象

镓位于元素周期表第四周期的第IIIA族,是一种少见的低熔点、高沸点金属,熔点为29.76°C,沸点为2403°C,被称为“液态金属”.常压下固态镓在熔化时密度反常增加,具有与水类似的反常现象.实验上主要通过中子散射、X射线吸收谱等手段[53,54]分析液态镓的结构随压强温度的变化趋势.2006年,Tien等[55]通过核磁共振谱方法在受限体系中观察到液态镓中存在两个分立的峰,分别位于260 K和220 K,说明受限的液体镓存在两种结构.Carvajal Jara等[33]通过分子动力学模拟发现镓中存在LDL和HDL两种液态,并且通过升压降压回路磁滞现象的消失预测了液体-液体相变临界点的位置(P=−2.5 GPa,T=450 K).Cajahuaringa等[56]研究了液态镓的动力学性质,他们通过分析系统的均方位移和自散射函数发现系统在液体-液体相变发生前存在明显的动力学不均匀性,并且发现两种液态的动力学差别很大,高密度态的扩散率比低密度态的大1—2个数量级.

3.1 液体镓的密度反常

Tien等[55]的实验和Carvaajal Jara等[33]的模拟计算都说明镓中存在一级液体-液体相变.李任重等[40]近期的工作则关注具有液体-液体相变的镓是否也具有类似于水的反常特性,他们用分子动力学模拟研究了液态镓的热力学、动力学、结构等性质,及其与液体-液体相变的关联.图6是镓的相图[40],李任重等发现随着温度的降低,相图中出现等密度线相交的区域.在这些等密度线的交点,压强和温度相同但存在两种不同的密度,即在某一压强温度下存在两种不同的液体.这说明液态镓存在液体-液体相变,且其液体-液体共存线为负斜率,与水的液体-液体共存线类似.

镓也存在类似于水的密度反常现象.根据一般的热力学关系,

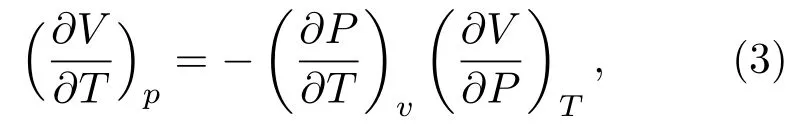
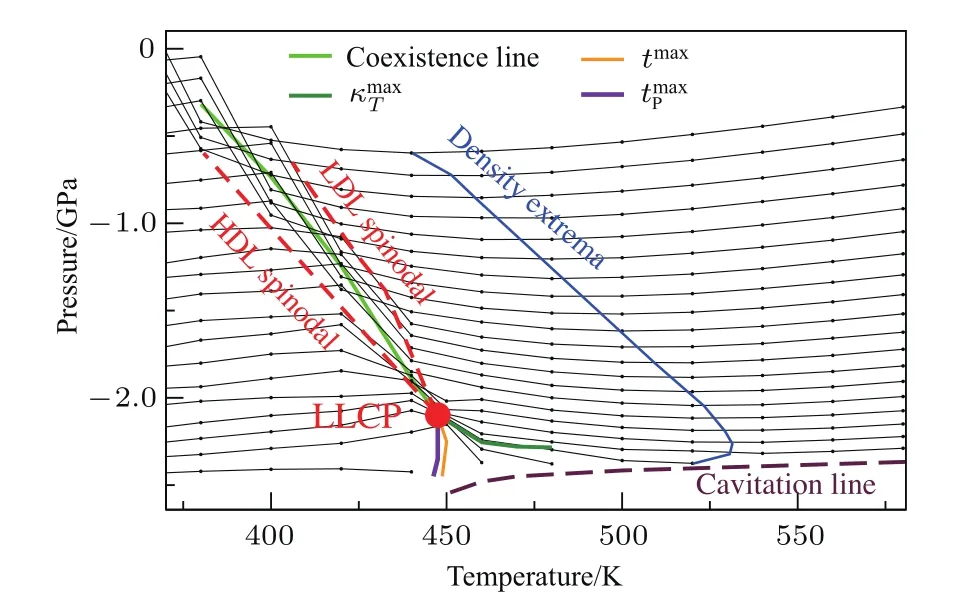
图6 镓的相图 旋结线用红色虚线表示,气液旋结线用紫色虚线表示,共存线用绿色线表示,密度极大值轨迹用蓝色线表示;液体-液体临界点作为共存线的终点,用红色圆点表示;三条响应函数极值线,定压比热容Cpm ax、等温压缩系数κx、平移序参量对温度的导数(dt/dT)max,分别用紫色、深绿色、橘色表示[40]Fig.6.The phase diagraMof gallium.The LLCP is located as the terminal point of coexistence line.The thermodynamic anomaly,speci fi c heat maximuMCpm ax(purple line),the compressibility maximuMκmT ax(dark green),and the response function maximuMof the translational order parameter(dt/dT)max(orange line).The spinodal lines(red line),the cavitation line(purple line),the coexistence line(green line),and the temperature of density extrema are also presented[40].

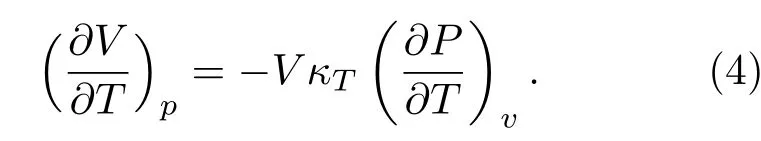
因为体系的等温压缩系数始终为正(液体在压缩时体积会变小),而密度极值定义为(∂V/∂T)p=0,因此推导后可以等价为(∂P/∂T)v=0,也就是在压强-温度相图中的等密度线极值处,如图6所示.密度极值的轨迹包围的区域就是密度反常区域,在这个区域内沿着等压线升温,系统的体积反而会下降(违背热胀冷缩现象).

3.2 液体镓的动力学和结构反常

李任重等[40]还研究了液态镓的动力学反常和结构反常.他们发现液态镓的扩散系数在某一相区间内反常地随着密度的增大而增大,如图7(a)所示.这种扩散反常现象与水和类水物质中观察到的现象类似[30,50].此外,他们还通过定义平移对称性的序参量t,t≡|g(r)−1|dr,研究了结构特性,其中g(r)是体系的对关联函数.参量t越大,体系越有序.他们发现当密度增加时液态镓的平移序参量会先下降再上升,如图7(b)所示,说明系统的有序度先下降再升高.然而,一般液体的有序度会随体系压缩而单调地增加,因此液态镓中存在结构反常区域,而且与SPC/E模型下的水结论类似[57].

图7 不同温度下扩散系数和平移序参量随密度的变化趋势示意图 (a)扩散系数有极大值,代表存在动力学反常区间;(b)平移序参量有极小值,代表存在结构反常区间[40].Fig.7. The di ff usion coefficient and the translational order parameter along isotherms as a function of density:(a)Di ff usivity anomaly;(b)structural anomaly[40].

3.3 液体镓的热力学反常

李任重等[40]又进一步研究了液体-液体超临界区内临界点附近的热力学特性.如图8所示,体系的焓H、密度ρ等状态参量在超临界区沿着等压线或者等温线单调地连续变化,但是其响应函数,如定压比热容Cp=、等温压缩系数κT= −等,对温度的导数会出现极大值,且越接近临界点极值越大.不同响应函数极值点的连线在液体-液体临界点附近逐渐汇聚成Widom线,并终止于临界点.镓的这一超临界现象与液态氢-原子氢的液体-液体临界点附近的超临界现象以及类水物质中的超临界现象类似[18,49,50].

简而言之,镓具有类似于水的负斜率液体-液体相变共存线,也存在着密度反常、扩散率反常、热力学反常、结构反常等,这些特性和被预测有液体-液体相变的一系列材料[1,2,6,58]一致.

4 总结与展望

主要介绍了具有液体-液体相变的一类材料及其反常特性,包括高温高压下氢的液体-液体相变及其超临界现象,镓的反常特性及其与液体-液体相变的关联等.李任重等[18,40]的研究发现高压下氢存在分子液态氢到原子液态氢的一级相变,在超临界区存在热力学反常现象,同时也具有与水类似的密度反常和负斜率液体-液体相变共存线;第III主族的单质镓存在液体-液体相变,也具有与水类似的密度、热力学、动力学、结构等反常现象.这些材料的化学性质完全不同,却具有类似的反常物理特性,说明反常现象的根源与液体-液体相变密切相关.

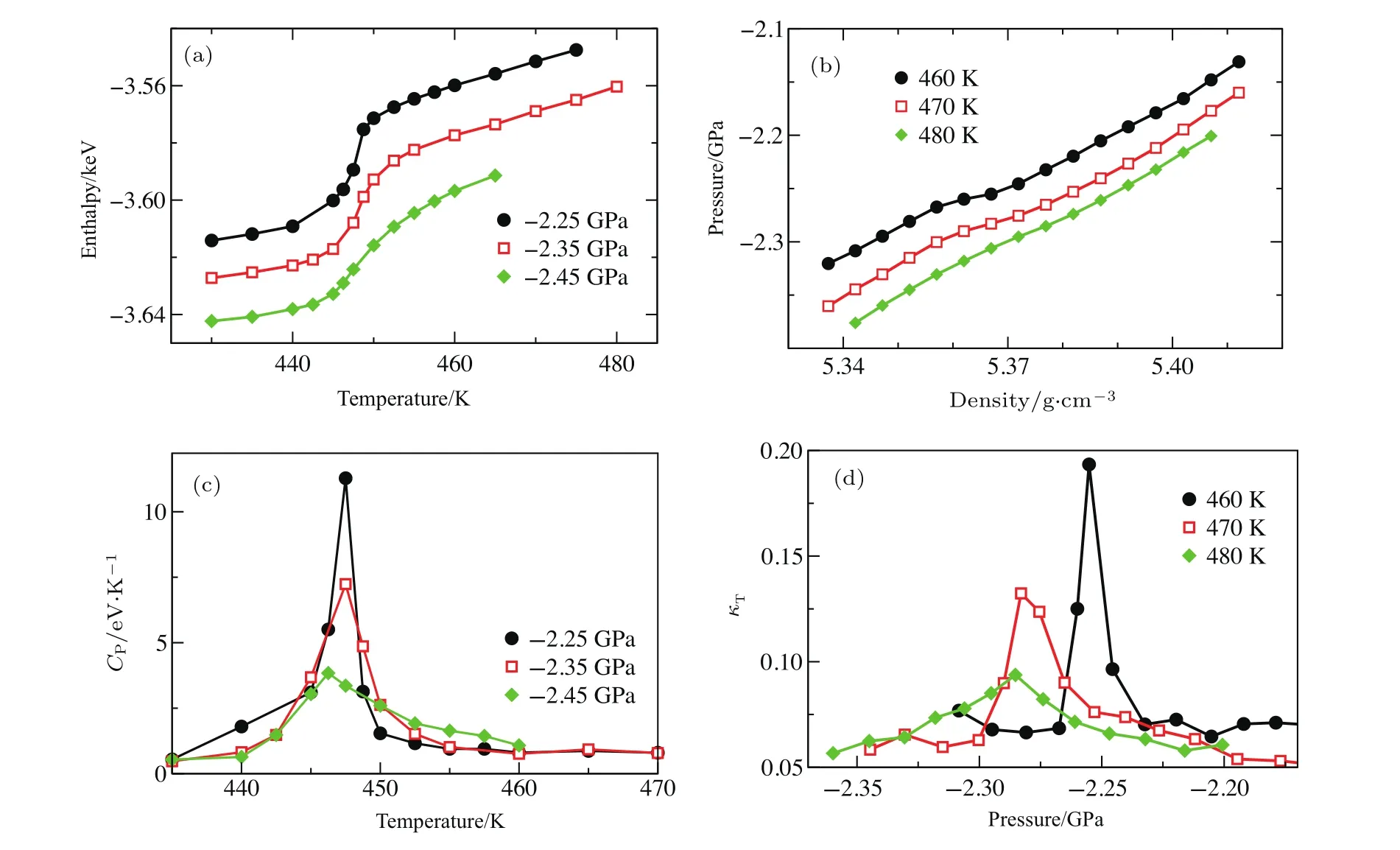
图8 在液(体-液)体 临界点以外的超临界区,镓的状(态函数)和 响应函数示意图 (a)焓H;(b)密度ρ;(c)定压比热容Cp=;(d)等温压缩系数κT=−[40]TFig.8.State function and response function beyond the LLCP in supercritical region:(a)Enthalpy H;(b)density ρ;(c)Cp;(d) κT[40].

简要地探讨了多种复杂液体的热力学、动力学、结构的反常行为及其原因,发现一类材料在宏观物理性质上展现出类似水的反常特性,很可能与液体-液体相变密切关联.这些研究对进一步理解复杂液体的性质及其应用具有重要的参考意义,也为实验的解释和预测提供了一定的理论基础.

[1]Speedy R J,Angell C A 1976 J.Chem.Phys.65 851

[2]Angel C A,Shuppert J,Tucker J C 1973 J.Phys.Chem.77 3092

[3]Debenedetti P G 2003 J.Phys.Condens.Matter 15 R1669

[4]Angell C A,Sichina W J,Oguni M1981 Tech.Report

[5]Angell C A 2004 Annu.Rev.Phys.Chem.55 559

[6]Kumar P,Stanley H E 2011 J.Phys.Chem.B 115 14269

[7]Sato H,Watanabe K,Levelt Sengers J MH,Gallagher J S,Hill P G,Straub J,Wagner W 1991 J.Phys.Chem.Ref.data 20 1023

[8]Conde O,Teixeira J,Papon P 1982 J.Chem.Phys.76 3747

[9]Kanno H,Angell C A 1979 J.Chem.Phys.70 4008

[10]Errington J R,Debenedetti P G 2001 Nature 409 318

[11]Ball P 2008 Nature 452 291

[12]Sastry S,Debenedetti P G,Sciortino F,Stanley H E 1996 Phys.Rev.E 53 6144

[13]Angell C A 2008 Science 319 582

[14]Poole P H,Sciortino F,Essmann U,Stanley H E 1992 Nature 360 324

[15]Sastry S,Angell C A 2003 Nat.Mater.2 739

[16]Saika-Voivod I,Sciortino F,Poole P H 2000 Phys.Rev.E 63 11202

[17]Morales MA,McMahon J M,Pierleoni C,Ceperley D M2013 Phys.Rev.Lett.110 65702

[18]Li R,Chen J,Li X,Wang E,Xu L 2015 New J.Phys.17

[19]Liu Y,Panagiotopoulos A Z,Debenedetti P G 2009 J.Chem.Phys.131 9473

[20]Poole P H,Saikavoivod I,Sciortino F 2005 J.Phys.Condens.Matter 17 L431

[21]Harrington S,Poole P H,Sciortino F,Stanley H E 1997 J.Chem.Phys.107 7443

[22]Yamada M,Mossa S,Stanley H E,Sciortino F 2002 Phys.Rev.Lett.88 195701

[23]Brovchenko I,Geiger A,Oleinikova A 2005 J.Chem.Phys.123 44515

[24]Sciortino F,La N E,Tartaglia P 2003 Phys.Rev.Lett.91 155701

[25]Mishima O,Stanley H E 1998 Nature 392 164

[26]Glosli J N,Ree F H 1999 Phys.Rev.Lett.82 4659

[27]Mukherjee G D,Boehler R 2007 Phys.Rev.Lett.99 225701

[28]Boates B,Bonev S A 2009 Phys.Rev.Lett.102 15701

[29]Morales MA,Pierleoni C,Schwegler E,Ceperley D M2010 Proc.Natl.Acad.Sci.USA 107 12799

[30]Vasisht V V,Mathew J,Sengupta S,Sastry S 2014 J.Chem.Phys.141 124501

[31]Vasisht V V,Saw S,Sastry S 2011 Nat.Phys.7 549

[32]Katayama Y,Mizutani T,Utsumi W,Shimomura O,Yamakata M,Funakoshi K 2000 Nature 403 170

[33]Carvajal Jara D A,Fontana MM,Antonelli A,De K M2009 J.Chem.Phys.130 221101

[34]Bhat M,Molinero V,Soignard E,Solomon V,Sastry S,Yarger J,Angell C 2007 Nature 38 787

[35]Brazhkin V V,Popova S V,Voloshin R N 1999 Phys.B:Condens.Matter 265 64

[36]Cadien A,Hu Q Y,Meng Y,Cheng Y Q,Chen MW,Shu J F,Mao H K,Sheng H W 2013 Phys.Rev.Lett.110 125503

[37]Greaves G N,Wilding MC,Fearn S,Langsta ffD,Kargl F,Cox S,Van Q V,Majérus O,Benmore C J,Weber R,Matin C M,Hennet L 2008 Science 322 566

[38]Sheng H W,Liu H Z,Cheng Y Q,Wen J,Lee P L,Luo W K,Shastri S D,Ma E 2007 Nat.Mater.6 192

[39]Zeng Q S,Ding Y,Mao W L,Yang W,Sinogeikin S V,Shu J,Mao H K,Jiang J Z 2010 Phys.Rev.Lett.104 105702

[40]Li R,Sun G,Xu L 2016 J.Chem.Phys.145 54506

[41]Shell MS,Debenedetti P G,Panagiotopoulos A Z 2002 Phys.Rev.E 66 11202

[42]Weir S T,Mitchell A C,Nellis W J 1996 Phys.Rev.Lett.76 1860

[43]Fortov V E,Ilkaev R I,Arinin V A,Burtzev V V,Golubev V A,Iosilevskiy I L,Khrustalev V V,Mikhailov A L,Mochalov MA,Ternovoi V Y 2007 Phys.Rev.Lett.99 185001

[44]Delaney K T,Pierleoni C,Ceperley D M2006 Phys.Rev.Lett.97 235702

[45]Holst B,Redmer R,Desjarlais MP 2008 Phys.Rev.B 77

[46]Scandolo S 2003 Proc.Natl.Acad.Sci.USA 100 3051

[47]Bonev S A,Militzer B,Galli G 2004 Phys.Rev.B 69 1985

[48]Pierleoni C,Morales MA,Rillo G,Holzmann M,Ceperley D M2016 Proc.Natl.Acad.Sci.USA 113 4953

[49]Xu L,Kumar P,Buldyrev S V,Chen S H,Poole P H,Sciortino F,Stanley H E 2005 Proc.Natl.Acad.Sci.USA 102 16558

[50]Xu L,Buldyrev S V,Angell C A,Stanley H E 2006 Phys.Rev.E 74 31108

[51]Liu L,Chen S H,Faraone A,Yen C W,Mou C Y 2005 Phys.Rev.Lett.97 716

[52]Rose MC,Cohen R E 2012 Phys.Rev.Lett.109 187604

[53]Comez L,Cicco A Di,Itie J P,Polian A 2001 Phys.Rev.B 65 853

[54]Wei S,Oyanagi H,Liu W,Hu T,Yin S,Bian G 2000 J.Non.Cryst.Solids 275 160

[55]Tien C,Charnaya E V,Wang W,Kumzerov Y A,Michel D 2006 Phys.Rev.B 74 24116

[56]Cajahuaringa S,de Koning M,Antonelli A 2012 J.Chem.Phys.136 64513

[57]Yan Z,Buldyrev S V,Kumar P,Giovambattista N,Debenedetti P G,Stanley H E 2007 Phys.Rev.E 76 51201

[58]Corsetti F,Artacho E,Soler J M,Alexandre S S,Fernandezserra MV 2013 J.Chem.Phys.139 194502

PACS:64.70.Ja,64.30.–t,64.10.+h,64.60.F–DOI:10.7498/aps.66.176410

*Project supported by the National Basic Research PrograMof China(Grant No.2015CB856801),the National Natural Science Foundation of China(Grant No.11525520),and the China Postdoctoral Science Foundation Funded Project(Grant No.2017M610687).

†Corresponding author.E-mail:limei.xu@pku.edu.cn

Liquid-liquid phase transition and anomalous properties∗

Li Ren-Zhong1)Wu Zhen-Wei1)Xu Li-Mei1)2)†

1)(International Center for QuantuMMaterials,School of Physics,Peking University,Beijing 100871,China)
2)(Collaborative Innovation Center of QuantuMMatter,Beijing 100871,China)

26 June 2017;revised manuscript

16 August 2017)

In most of liquids,densities increase as temperature decreases.However,the densities of water and water-like liquids,such as silicon and germanium,are anomalous,which increase as temperature increases.Such substances also show other anomalous behaviors,such as di ff usivity anomalies(di ff usivities increase as density increases),and thermodynamic anomalies(the fl uctuations increase as temperature decreases).The chemical properties of these materials are very di ff erent froMeach other,but they all share similar physical properties.Further studies indicate that most of theMhave two distinct liquid states,i.e.,a low-density liquid and a high-density liquid,and a fi rst order liquid-liquid phase transition(LLPT)between these two liquids.We mainly discuss the anomalous properties of materials each of which has a predicted LLPT and their relations with anomalous behaviors(thermodynamic,dynamic and structural)as those of water and water-like liquids,such as hydrogen and gallium.In particular,we discuss the supercritical phenomenon of the liquid-liquid phase transition of hydrogen,as well as the liquid-liquid phase transition of galliuMand its relation with the thermodynamic,dynamic,and structural anomalies.It is found that the liquid hydrogen and galliuMboth have the LLPT and share similar anomalous behaviors as water and water-like liquids,such as density anomaly,dynamics anomaly,thermodynamic anomaly Since the chemical properties of these materials are very di ff erent froMthose of others having the LLPT,the anomalous behaviors may be common features for substances predicted to have the LLPT.

liquid-liquid phase transition,supercritical phenomenon,anomalous behaviors,WidoMline

10.7498/aps.66.176410

∗国家重点基础研究发展计划(批准号:2015CB856801)、国家自然科学基金(批准号:11525520)和中国博士后科学基金(批准号:2017M610687)资助的课题.

†通信作者.E-mail:limei.xu@pku.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn