蚁群算法的参数分析

文/谭慧莉

蚁群算法的参数分析

文/谭慧莉

在详细分析了蚁群算法的数学模型及综述当前国内外蚁群算法研究现状的基础上，文章重点对状态转移概率和信息素更新机制进行改进，并以旅行商问题(TSP)为例进行仿真实验，有效地避免了蚁群算法出现早熟和停滞的问题，验证了改进的合理性和有效性。

蚁群算法 TSP问题 状态转移概率信息素

当今社会已高速发展，各领域内不断的涌现出超大规模、随机性的复杂问题，传统的计算方法难于解决这些复杂问题。蚁群算法(ACA)是近年提出的解决这类复杂问题的一种模拟进化算法。最早，由意大利学者M.Dorigo等人于1991年在首届欧洲人工生命会议上提出。从此，蚁群算法逐渐引起了许多国家研究者的关注，大量有价值的研究成果陆续发表。

1 蚁群算法的数学模型

蚁群算法最初用于解决旅行商问题(TSP)。旅行商问题是一个经典的组合优化问题，是验证求解组合优化问题有效性的一个间接标准。

在自然界中，蚂蚁个体从蚁巢出发寻找食物源，会在所经过的路径上留下一种称为“信息素”的物质，后面蚂蚁在运动的过程中，能够感知这种物质的存在和强度，最终，找出蚁巢和食物源之间的最短距离。受蚁群觅食行为的启发，M.Dorigo等人提出了蚁群算法的基本思想，以n个城市的TSP问题(1,2,…,n分别表示城市的编号)为例，算法的数学模型是：

m—蚁群蚂蚁的数量

dij—城市i与j之间的距离(假定dij=dji)，i,j=1,2,…,n

bi(t)—t时刻位于城市i的蚂蚁的数量

ηij(t)—t时刻所能提供的某种启发式信息，

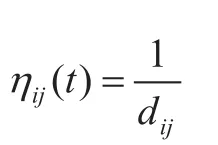
τij(t)—t时刻蚂蚁群在路径(i,j)上的信息素

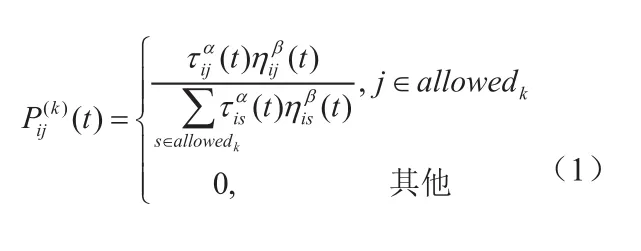
其中α为信息启发式因子，β为期望启发式因子，tabuk是蚂蚁k已走过的城市，表示t时刻蚂蚁k的禁忌表。

算法步骤：

（3）蚂蚁的禁忌表索引号k=1

（5）蚂蚁个体根据状态转移概率公式（1）计算的概率选择城市j并前进，

（6）修改禁忌表指针，即蚂蚁k移动到新的城市，并把该城市加到蚂蚁k的禁忌表中

（8）根据式(2)和(3)更新每条路径上的信息量

2 国内外的研究现状及分析

蚁群算法作为一种新型的模拟进化算法，具有正反馈机制，分布式计算，易与其他方法结合等很多优点。但是，蚁群算法也存在一些不足和缺陷，收敛速度慢、易于停滞等问题是目前重点解决的问题，针对以上缺陷，蚁群算法的主要研究内容集中在以下几个方面：

2.1 对蚁群内部分工协作的模拟

真实的蚁群社会中，不同蚂蚁分工不同，相互协作共同完成任务。对此进行模拟的多态蚁群算法中，引入多种蚂蚁群，不同蚂蚁群的信息素调控不同，在蚂蚁搜索过程中，针对各具体路径选择合适的信息素的浓度，加快寻优收敛速度。

2.2 缩短蚁群算法的搜索时间

L.M.Gambardella提出了一种修正的蚁群算法—蚁群系统，对蚂蚁寻路的规则进行了一定的调整；张军[7]等人对蚁群算法中的参数进行分析得到了较好的改进。

3 对蚁群算法参数的改进思路

针对蚁群算法容易出现局部最优解和停滞的的缺点，通过对文献[3,5,6,7]的深入研究，d对蚁群算法在以下两方面做出改进：

3.1 对状态转移概率的改进

修改公式（1）为

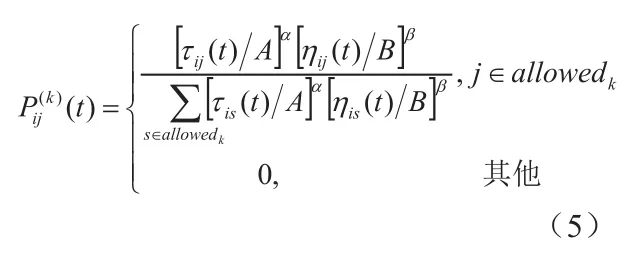
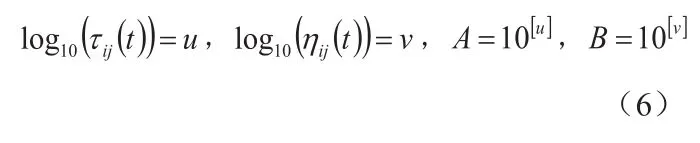
3.2 对信息素的改进

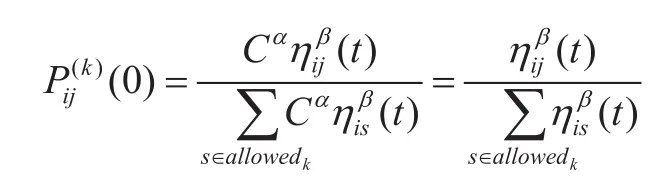
即蚁群创建的第一条路径时要参考城市之间的距离信息，导致蚁群留下的信息可能不准确，阻碍以后的蚂蚁发现更好的全局最优解。改进对策：

借鉴文献[8]中对最大可选城市数的分析：以城市i为中心，作半径为R的圆PCi，R从0不断扩大，直至取得i的临近城市为止时记录下圆内的城市数

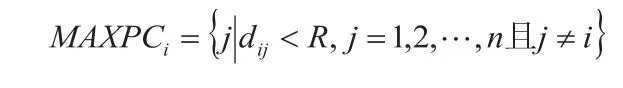
定义初始时刻信息素值

q为权值，0和1之间取值，将距离当前城市较远的初始信息素值设为较近城市的q倍。

4 实验结果与分析数据

选用TSPLIB基准库中的Oliver30问题进行试验，已知的Oliver30问题的最短路径长度为423.740 601，路径中蚂蚁的行走路线为：1—2—3—4—6—5—7—8—9—10—11—12—13—14—15—16—17—19—18—20—21—22—23—24—25—28—26—27—29—30。

由于算法中的参数选取对实验结果影响很大，采用了多组参数对实验结果进行分析，令Q=100，m=20，迭代200次的最优路径值为424.4611，蚂蚁的行走路线为：6—10—9—8—7—4—3—2—1—30—29—28—26—27—25—24—23—22—21—20—18—19—17—16—15—14—13—12—11—5。

5 结论语

本文在充分研究了蚁群算法在状态转移概率和信息素更新方面的缺陷的基础上，对蚁群算法进行改进，并通过TSP问题的仿真实验进行数据分析和比较验证了改进的有效性。

[1]M.Dorigo,C.Blum.Ant Colony Optimization Theory：ASurvey. Theoretical Computer Science,2005,344(2-3)：243-278.

[2]M.Birattari,P.Pellegrini,M. Dorigo.On the Invariance of Ant Colony Optimization.IEEE Transactions on Evolutionary Computation.2007,11(06)：732-742

[3]徐宗本.计算智能[M].北京：高等教育出版社,2004：111-123.

[4]M.Dorigo,L.M.Gambardella.Ant Colonies for the Traveling Salesman Problem. Bio-System,1997,43：73-81.

[5]鲍文杰.朱信忠.赵建民.徐慧英.加权值.多态蚁群算法[J].软件工程,2016(04)：1-4.

[6]L.M.Gambardella,M.Dorigo.Solving Symmetric and a Symmetric TSPs by Ant Colonies.Proceedings of the IEEE Conference on Evolutionary Computation,1996：622-627.

[7]张军,刘羽,程樊启.蚁群算法解决TSP问题的并行化研究与实现[J].计算机技术与发展,2011(05)：72-74.

[8]全 惠 云,文 高 进.求 解TSP的 子空间遗传算法[J].数学理论与应用,2002,22(01)：36-39.

作者单位 哈尔滨商业大学 黑龙江省哈尔滨市 150028

谭慧莉（1979-），女，理学硕士。哈尔滨商业大学讲师。研究方向为优化理论。