基于变步长迭代算法的微轴承参量特性研究
李家贤 张海军 刘全

摘 要: 利用变步长迭代算法在Matlab平台上对微轴承的修正模型进行仿真模拟。通过传统连续模型、一阶滑移修正及Wu新滑移修正模型的对比发现,在最小气膜间隙处各滑移修正模型得到的参量远低于连续模型的结果。而且当气膜间隙小于1 μm时,各模型之间的结果偏差随气膜间隙的减小而迅速放大,连续模型已不适于此条件下的特性分析,必须考虑滑移修正效应的影响,以便得到较精确的相关电子设备中的参量特性。
关键词: 变步长迭代算法; Matlab; 滑移修正模型; 微轴承
中图分类号: TN622+.1?34; TH117.2 文献标识码: A 文章编号: 1004?373X(2017)16?0010?03
Abstract: The variable step size iterative algorithm is used to simulate the modification model of the micro bearing in Matlab platform. It is found by comparison with the traditional continuum model, first?order slip correction model and Wu new slip model that the parameters obtained by all the slip correction models at minimum gas film clearance are far below the results got by the continuum model. When the gas film clearance is less than 1 μm, the deviation of results from each model increases rapidly with reduction of the gas film clearance. It means that the continuum model is not suitable for characteristic analysis under this condition. That′s why the influence of slip correction effects must be considered, so as to achieve accurate parametric characteristics of aerostatic bearing in the related electronic equipment.
Keywords: variable step size iterative algorithm; Matlab; slip correction model; micro bearing
0 引 言
微轴承是一种具有高回转精度,耐低温和高温及辐射等优良特性的精密电子元件。目前在PCB电子元件、精密电子设备、控制系统等领域中都得到了非常成功地应用[1?6]。但是现有微气体轴承承载的测量估算都只采用建立在无滑移修正条件上的传统连续模型。然而当气膜间隙尺寸达到亚微米级时,气体分子在固壁的滑移效应变得极其重要。在此条件下传统模型已失效,需采用经过修正的模型进行参量的分析[7?8]。
本文引入一阶滑移修正和Wu新滑移修正模型,然后在Matlab仿真平台[9]下采用变步长迭代算法[10]求解修正后的模型,并探讨修正后得到的精确参量特性。
1 修正改进模型
1.1 微轴承结构
图1所示电子设备中微轴承的转子直径为D,轴长为L,有两排沿周向均匀分布的节流孔,每排节流孔数为N,距最近轴端为l,孔径为d。转速为n,偏心距为e,气膜厚度为h。当e=0时,平均气膜间隙为hm。
1.2 滑移修正模型
图1所示的θ为周向角度,z为轴向坐标。则传统连续、一阶修正、及Wu新修正模型的无量纲化微轴承模型为:
式中:[Z=zL]为无量纲轴向坐标;[H=hhm=1+εcosθ]为无量纲气膜厚度;[ε=ehm]为偏心率;[P=ppa]为无量纲气压,p为气压,pa为标准气压;[Λ=μπn(r2)(5pah2m)]为压缩系数,μ为气体黏度;[Kn=λh]为当地克努森数,[λ]为平均自由程;[f=min[1Kn,1]];bs,cs为模型系数,见表1。
表1 Reynolds方程模型系数
划分网格时略去表面曲率的影响,并把节流孔当作一个网格点处理,如图2所示,阴影部分为离散点的控制体积单元。则求解式(1)的边界条件为:大气边界,[P(θ,Z=0)=1];周期边界,[P(θ,Z)=P(2π+θ,Z)];对称边界,[(?P?Z)(Z=0.5)=0]。
2 变步长迭代原理及变量修正计算
假设加压气源流经节流孔为绝热过程,则流出节流孔的流量为:
式中:[ρs]为气体密度;[ps]为气源压力;k为气体绝热指数;第σ个节流孔后气压为[p=pσ];[pσ]需根据图3所示的流入区域流量[Min,σ]和流出区域流量[Mout,σ]相等的流量守恒原理确定。对第σ个节流孔区域有:
[Min,σ=Mσ2+Mσ3-Mσ1-Mσ4] (3)
式中:[Min,σ=24μ?TMin,σ(p2ah3m)]为通过第σ个节流孔流入的无量纲化流量;[?]为空气的气体常数;[Mσ1],[Mσ2]分别为无量纲化周向流量;[Mσ3],[Mσ4]分别为无量纲化轴向流量,需根据滑移速度分布[7?8]修正计算为(同理可得[Mσ2]及[Mσ3]):
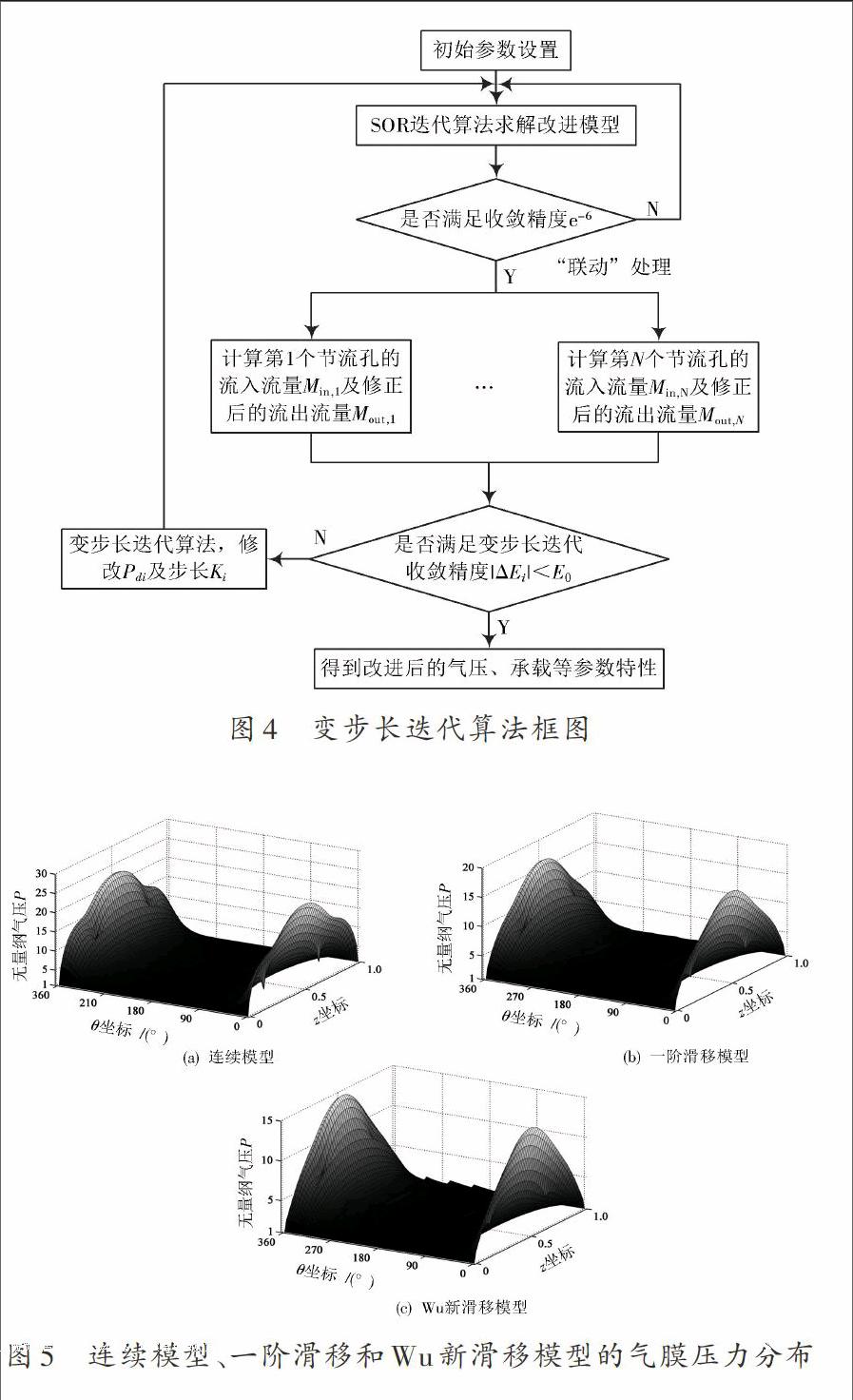
在图4所示算法流程框图中,使用SOR迭代算法[11]得到除孔后高精度的气压,再用变步长迭代算法求解孔后气压,最终对面积求积分得到由沿连心方向的WH和沿连心垂直方向的WV组成的刚度K为:endprint
[K=ΔW2H+W2VΔeWH=-20L202πpcosθ rdθdZWV=-20L202πpsinθ rdθdZ] (6)
3 结果与讨论
所研究的电子元件中的微轴承参数为转子半径4 mm,轴长0.8 mm,节流孔距最近轴端距离为[L4],节流孔数N=8,孔径为0.05 mm,气源压力为4×105 Pa。图5(a)~图5(c)分别为在平均气膜间隙hm=0.2 μm、偏心率ε=0.90,转速n=12 kr/min条件下沿θ=0°处的连续模型、一阶滑移和Wu新滑移模型的气压分布。可以发现各模型的气压在最小气膜间隙处远大于其余区域。这是因为此处的气膜间隙远小于其他区域,动压效应较强显著增大了气压。而远离此处气压主要靠气源压力起支承作用相对较小。通过对比发现在最小气膜间隙处,一阶滑移、Wu新滑移修正模型的气压明显小于连续模型且此条件下的最高偏差率分别达27.50%,36.17%,远超可接受的误差范围。在此条件下,为了得到精确的测量值,应考虑滑移修正的影响。
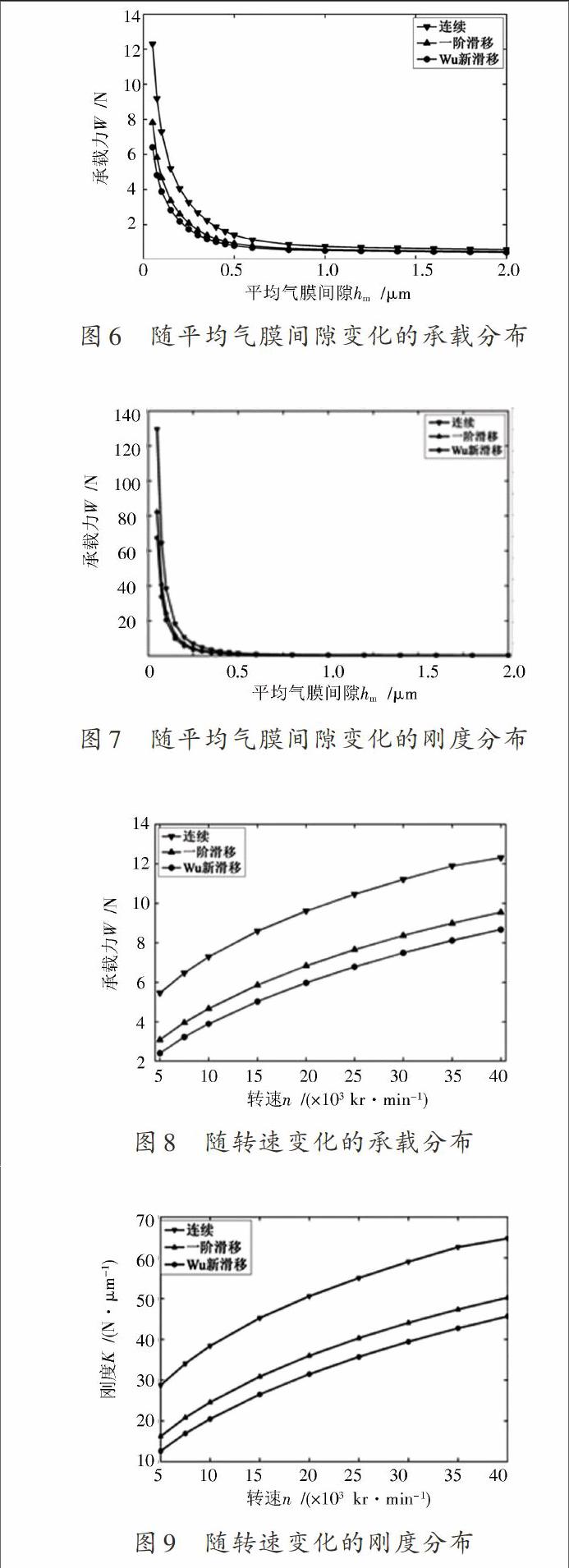
图6、图7分别为在偏心率ε=0.95、转速n=10 kr/min条件下,随气膜间隙的变化连续和各滑移修正模型的承载和刚度参量分布。可以发现当平均气膜间隙相对较大时,承载较弱、增幅较慢,承载力差异不明显。但当平均气膜间隙hm小于1.0 μm时,承载、刚度增幅变快且结果偏差随气膜间隙的减小而迅速放大。这是因为动压效应的增强使得承载变强、增幅变快,间接影响刚度的变化,此外在滑移效应的影响下最小气膜间隙处的气压显著降低。而大部分承载、刚度靠最小气膜间隙周围的气压生成,所以偏差随着滑移效应的增强被放大。图8、图9分别为在平均气膜间隙hm=0.2 μm、偏心率ε=0.95条件下,随转速的变化连续与各滑移修正模型的承载和刚度参量分布。可以发现在相对较低的转速5~10 kr/min条件下,由于动、静压效应的相互作用,无滑移与各滑移模型的承载和刚度增幅相对较快。但当转速大于10 kr/min后,动压增幅作用减弱使承载的增幅变缓,间接使得刚度增幅变缓。然而各模型之间的承载及刚度偏差在一定范围内随转速的增大有显著偏差。
4 结 语
滑移修正效应对电子设备中微轴承承载、刚度等参量特性的影响随气膜间隙的变化而改变显著;在小气膜间隙条件下,各滑移修正模型得到的参量远低于连续模型的结果,而且参量之间的偏差随气膜间隙的减小而迅速放大,必须考虑滑移效应的影响;通过变步长迭代算法求解滑移修正模型可得到较精确的微轴承参量特性分布,以便为相关电子设备、控制系统的安全运行提供精确数据及为相关参量的估算提供坚实的理论基础。
参考文献
[1] WANG C C, YAU H T, KUO C L. Bifurcation and chaos analysis of a relative short spherical air bearing system via a novel hybrid method [C]// 2009 International Workshop on Chaos Fractals Theories and Applications. [S.l.]: IEEE, 2009: 327?330.
[2] CHEN M F, HUANG W L, CHEN Y P. Design of the aerostatic linear guide way with a passive disk?spring compensator for PCB drilling machine [J]. Tribology international, 2010, 43(1): 395?403.
[3] DE MOURA E P, SOUTO C R, SILVA A A, et al. Evaluation of principal component analysis and neural network performance for bearing fault diagnosis from vibration signal processed by RS and DF analyses [J]. Mechanical systems and signal processing, 2011, 25(5): 1765?1772.
[4] 喻丽华,谢庆生,李少波,等.钻削电主轴空气静压径向轴承润滑参数优化[J].机械设计与制造,2014(8):124?126.
[5] 张洪飞,闫守成.实时汽车电子辅助制动控制系统的设计研究[J].现代电子技术,2016,39(1):153?156.
[6] 巫发茂,蒋龙,王健,等.基于ANSYS Workbench某机载电子设备随机振动响应分析[J].现代电子技术,2016,39(10):96?99.
[7] BURGDORFER A. The influence of the molecular mean free path on the performance of hydrodynamic gas lubricated bearings [J]. Transactions on ASMR, 1959, 81: 94?100.
[8] WU L. A slip model for rarefied gas flows at arbitrary Knudsen number [J]. Applied physics letters, 2008, 93(25): 253103.
[9] 王若楠,田野,马玉峰,等.Matlab程序单步调试方法及样例分析[J].现代电子技术,2015,38(15):139?141.
[10] ZHENG S F, JIANG S Y. Improved finite different method for pressure distribution of aerostatic bearing [J]. Journal of Southeast University, 2009, 25(4): 501?505.
[11] 刘丽华,马昌凤,唐嘉.求解广义鞍点问题的一个新的类SOR算法[J].计算数学,2016(1):83?95.endprint

