中国第一部三角学译著《大测》的底本与版本研究

董 杰 陈建平

(1.内蒙古师范大学科学技术史研究院，呼和浩特 010022； 2.明尼苏达州州立大学圣克劳德分校数学统计系，美国明尼苏达州 56301)

中国第一部三角学译著《大测》的底本与版本研究

董 杰1陈建平2

(1.内蒙古师范大学科学技术史研究院，呼和浩特 010022； 2.明尼苏达州州立大学圣克劳德分校数学统计系，美国明尼苏达州 56301)

明末传教士邓玉函以毕的斯克斯1612年版《三角法》为底本，并采用斯蒂文著作《数学记录》中部分内容，编译出中国第一部三角学著作《大测》，将欧洲当时最新、最重要的三角学成果介绍到中国，对中国三角学影响极大。其造表所用的六宗三要二简法，成为17—18世纪中国三角函数造表法的模式。对《大测》诸版本进行梳理可知，《崇祯历书》本成书最早，《西洋新法历书》本影响最大，《新法算书》文津阁本讹误最少。浙江图书馆藏文澜阁《四库全书》中的《大测》实为丁丙补抄而成。除《新法历书》本和丁氏补抄本外，其他历次重修都对《大测》内容有所订正，体现出编纂人员工作认真，同时也具备一定的数学素养。文章通过《大测》底本与版本的研究，展现出该书更真实的动态演变过程，藉此窥得《崇祯历书》在清代的沿革。研究也将对《大测》乃至《崇祯历书》的校勘工作有所助益。

大测底本 三角学 崇祯历书

16世纪，随着通往东方新航路的开辟，欧洲传教士络绎东来，开启了中西文化间大规模交流。此时适逢明末《大统历》屡屡有误，历局依靠中国传统的数学、天文学知识已无法解决出现的问题。在徐光启(1562—1633)的领导下，中外学者共同翻译编纂大型科技丛书——《崇祯历书》。《崇祯历书》是中国古代最大的天算引进项目，对清代数学、天文学发展影响极其深刻[1]。此外，《崇祯历书》在清代也经历了十分复杂的演变过程。清兵入关之后，汤若望(1591—1666)将《崇祯历书》重编为《西洋新法历书》进呈新朝。之后南怀仁(1623—1688)又删去“西洋”二字，将其改名为《新法历书》。乾隆时又编撰《四库全书》，因避讳将该书易名为《新法算书》[2]。前人学者已对此书有相当的研究。朱家溍指出《西洋新法历书》《新法历书》《新法算书》与《崇祯历书》相比，书名、编译者职衔等文字信息的变化[3]。王渝生认为汤若望将《崇祯历书》删并修补成《西洋新法历书》，其间有他创造性的劳动[4]。江晓原较前人更为详细阐明《崇祯历书》在清代的演变情况，指明《崇祯历书》中最重要、也最有价值的“法原部”原文原图被收录在《古今图书集成·历象汇编·历法典》中[5]。祝平一则细致地对比分析了《崇祯历书》与《西洋新法历书》所含书籍及卷数、人员分工方面的异同，认为汤若望在编辑《西洋新法历书》时，主要在改动封面的版面与校订各表的数据。《崇祯历书》的几次重编虽有增删，但内容大致相去不远。虽然算表部分不断更新，但理论性的历算部分变动不大[6]。

从《崇祯历书》到《西洋新法历书》，其内容的调整和改动所反映出的信息，就如同西方历算在17、18世纪中国的一部生命史[7]。明末《崇祯历书》刊刻之后，仍不断修订，且卷帙浩大，有百余卷之多[8]，对其全部内容进行比对的工作，将会十分费时耗力。目前学界已经开始关注《崇祯历书》改编为《西洋新法历书》后某些内容被删减所揭示出的历史信息[9]。本文选取《崇祯历书》“法原部”著作《大测》，比对欧洲底本到汉译本以及该书在历次重修中内容的变化，借此呈现除政治因素影响外，《崇祯历书》在清代屡次重编的动态过程。

1 《大测》的底本判断

《大测》由德国传教士邓玉函(Johannes Schreck，1576—1630)与历局人员合作翻译编撰而成。1631年(崇祯四年)正月，徐光启第一次进《历书》一套，包括“法原部”《日躔历指》一卷、《测天约说》二卷、《大测》二卷；“法数部”《日躔表》二卷、《割圆八线表》六卷、《黄道升度表》七卷、《黄赤距度表》一卷；“会通部”《通率表》二卷[10]。其中《大测》是中国第一部三角学著作，对清代三角学，尤其是三角函数造表法发展影响巨大[11]。

方豪[12]、严敦杰[13]曾撰文探寻《大测》内容的西方来源。白尚恕经过比对，认为邓玉函编译《大测》时使用的底本为毕的斯克斯(Bartholomaeus Pitiscus，1561—1631)的《三角法》(Trigonometriae，1612)和斯蒂文(Simon Stevin，1548—1620)的《数学记录》(MémoiresMathématiques，1608)[14]。这为研究《大测》的底本提供了重要线索。但《三角法》有1608、1612年两个版本，《数学记录》也有荷兰文、拉丁文和法文三种版本，已有研究并没有给出判断的依据，因而有必要做进一步的厘清。

《三角法》的全称是TrigonometriaeSiueDeDimensioneTriangulorumLibriQuinqueItemProblematumVariorumNempeGeodaeticorum，Altimetricorum，Geographicorum，Astronomicorum:LibriDecem。中国学界一般译为《三角法》，是16—17世纪欧洲三角学体系构建过程中非常重要的一部著作。《三角法》有1608年和1612年两个版本[15]。《大测》表法篇“要法三”中的系法示例为判断邓玉函在编译《大测》时参照的底本提供了线索。示例中言：“甲辛上方为一七九四九一九三四四五一六，并之，得二六七九四九一九三四四五一六”。1608年版《三角法》此处2个数值分别为17744919544536和26744919344536。而1612年的版本中，此处2个数值分别为1794919344516和26794919344516，与《大测》中数值一致。由此推知邓玉函编译《大测》时参照的应是1612年版(图1)。经计算验证，1612年版本数值正确。

《三角法》一书的作者毕的斯克斯1561年出生于奥地利统治的格林贝格(Grünberg，现在波兰治下)。历史学家们对毕的斯克斯的生平所知不是很多，只知他在采尔布斯特(Zerbst)与海德尔堡(Heidelberg)念神学，是一个加尔文教徒(Calvinist)。作为一个加尔文教徒的数学家，毕的斯克斯被任命担任10岁的佛瑞德里克四世(Frederick IV)的教师，后又成为宫庭牧师[16]。16世纪欧洲三角函数表的建构，是先编造正弦表、余弦表，再用函数间的基本关系，造出其他函数表。因正切、正割值以余弦值为分母来计算，在余弦值接近零，即角度接近90°时，正切、正割值非常大。因而在此数值附近，余弦值的小误差会导致正切、正割值非常大的误差。毕的斯克斯计算出了每隔十秒的函数表，将研究成果发表于《三角学精义准则》(Magnuscanondoctrinaetriangulorum)，因而被欧洲学术界誉为“无与伦比的权威”，一直到20世纪初才由其它更精确的表所取代[17]。今天英语三角学“trigonometry”一词，就是从毕的斯克斯的著作《三角法》演变而来。

图2 《数学记录》(Hypomnema-ta mathematica)1608年版

《数学记录》的作者斯蒂文，明末多译为西门或西满。斯蒂文出生于布鲁基(Bruges，现在比利时治下)，是奥兰治的威廉治下一个反对天主教的西班牙新教教派支持者，其他详细的生平甚少有记录可寻。斯蒂文是个博学多产的学者，他多而互异的著作正表现了在其在生命不同阶段的经历。斯蒂文曾当过收银员与记账员，后来可能为其家乡布鲁基提供财政方面的服务。因为这样的经历，斯蒂文后出版了有关计算利息的利率表及其造表法的书。1581年，斯蒂文暂居在莱顿(Leiden)，并于1583年获准进入莱顿大学就读，毕业留校担任莱顿大学数学教师，拿骚(Nassau)的莫里斯王子是斯蒂文的学生之一。1590年，斯蒂文迁居代尔夫特(Delft)，在当地建造了新的风车模型，得到了专利，于1592年被任命掌管当地的水道事宜。1593年，由于莫里斯王子的推荐，斯蒂文成为军需官主任。1600年，斯蒂文负责组织莫里斯王子在莱顿大学工学院的数学教育。莫里斯王子对科学有真挚的爱好，因此与斯蒂文有密切的交流，许多斯蒂文的科学著作是这一密切的交流的成果，例如他最重要的数学著作之一《数学记录》就是此一交流的成果[18]。

《数学记录》原以荷兰文所著，1605—1608年出版，有3册共5部分组成。该书基本包含了斯蒂文教莫里斯王子的数学讲课笔记，涵盖的内容甚广，堪称当时的数学百科全书。《数学记录》并有拉丁文本与法文本。拉丁文本书名为Hypomnematamathematica(图2)，共5卷，第1卷包含造表原理与表[19]。《大测》中的部分知识，即来源于此。法文本书名为Mémoiresmathématiqves，共1函4部分。其中第4部分的首页写着第5册，内容也与荷兰文、拉丁文本第5册相同。显然原书第4册并没有翻译成法文出版。毕的斯克斯的《三角法》、斯蒂文的《数学记录》均由耶稣会士带到中国，藏于北堂图书馆[20]。邓玉函在编译《大测》时是以1612年版《三角法》为底本，同时参考了《数学记录》中的一些内容。

2 《大测》版本梳理

入清之后《崇祯历书》几度重编易名。本文在前人研究成果基础上，大致梳理出《大测》在清代的版本流变情况：明末刻印的《崇祯历书》本，1646年汤若望重编的《西洋新法历书》本，1673年南怀仁改名之后的《新法历书》本，《古今图书集成·历法典》所含《大测》(《古今图书集成》本)，《四库全书》中《新法算书》本(《新法算书》文渊阁本、《新法算书》文津阁本、《新法算书》文澜阁本)。《大测》诸版本基本情况介绍如下。

2.1 《崇祯历书》本

存世的《崇祯历书》多为残本，散见于北京故宫博物院、“台湾中央研究院”、梵蒂冈图书馆、韩国首尔大学奎章阁等地。潘鼐先生经过十多年的广查搜集与勘校补阙，汇集成一部《崇祯历书》，包括《大测》在内的明刻明印本占全书23种中的19种，2009年由上海古籍出版社影印出版。此外，2006年内蒙古大学出版社曾试印《明〈崇祯历书〉辑稿》若干套。《崇祯历书》和《明〈崇祯历书〉辑稿》中的《大测》一书完全相同。

《崇祯历书》本每半页九行，每行廿二字，标目行高一字，左右双线，白口，版心上方为节次目，下方页数。扉页题有“崇祯历书”四大字，后为“崇祯历书法原部大测一卷”基本目、节次目一行；次为“钦差礼部尚书兼翰林院学士恊理詹事府事加俸一级徐光启奉敕勑督修”二行；再次为“极西耶稣会士邓玉函撰，同会龙华民、罗雅谷同订，郑洪猷、陈应登、陈于阶仝较梓”等编撰人员姓名与分工(图3)[21]。《崇祯历书》本是《大测》最早的一个版本，在与拉丁文底本进行对比工作时尤为重要。

图3 《崇祯历书》本

2.2 《西洋新法历书》本

顺治改元后，汤若望将明版历书21种、75卷，另新增历书9种、18卷，合共30种、93卷，再加《奏疏》10卷，总计103卷，外再加《赤道南北两总星图》8幅，汇编为《西洋新法历书》进呈[22]。北京故宫博物院藏顺治二年(1654)补刊本，为国内外唯一仅存的足本[23]。20世纪末，北京故宫博物院联合海南出版社印行了一部包括经、史、子、集四部所属各种古籍的大型丛刊——《故宫珍本丛刊》，其中清顺治二年(1654)颁行的《西洋新法历书》被汇为五册(第三八三——三八七册)，归入天文算法类影印出版，《大测》二卷被第三八七册收入，此为《西洋新法历书》本。

《西洋新法历书》本实与《崇祯历书》本为同一书版印制，仅将扉页“崇祯历书”剜改为“西洋新法历书”，原扉页内“钦差礼部尚书兼翰林院学士协理詹事府事加俸一级徐光启奉敕勑督修”二行，易为“明礼部尚书兼翰林院学士协理詹事府事加俸一级徐光启督修”，并将撰、订一干人等易为“修政历法极西耶稣会士邓玉函撰汤若望订门人陈应登郑洪猷陈于阶潘国祥周胤刘有庆受法”(图4)[24]。值得关注的是，《西洋新法历书》本还改正了《崇祯历书》本中若干数值错误(详见后文)。之后《大测》的各种版本，大多在《西洋新法历书》本的基础上重抄或者重编。因此《西洋新法历书》本在《大测》版本递变过程中起到了承上启下的作用，汤若望功不可没。

图4 《西洋新法历书》本

2.3 《新法历书》本

1666年(康熙五年)汤若望去世后，比利时传教士南怀仁对《西洋新法历书》进行重新修订出版，此为《新法历书》本(图5)[25]。翻阅可知，《新法历书》中《大测》的封面虽改为“新法历书”，但首页及版心仍然为“西洋新法历书”。南怀仁在将《西洋新法历书》重新修订出版时，重点放在星表、算表等的修订上，对于理论性的天文、数学部分，仅是将封面替换为“新法历书”，内容则完全照搬。

图5 《新法历书》本

《西洋新法历书》和《新法历书》都是在《崇祯历书》书版的基础上剜改个别地方印制而成，故3种可统称为“明刻本”。

2.4 《古今图书集成》本

图6 《古今图书集成》本

据清刘铎所辑《古今算学丛书》(1898)载，《大测》尚有“历法典本”[26]，此即《古今图书集成》中所含《大测》。《古今图书集成》是清代编纂的一部类书，编纂工作始于1700年(康熙三十九年)，于1726年(雍正四年)用铜活字排版印成，世称“殿本”。民国时，上海中华书局依康有为所藏的雍正铜活字印本为底本，采用江南造纸厂机制连史纸，三开大本，以原书9页裁去边框中缝合为1页，缩小影印了《古今图书集成》，又称“九合一本”[27]。中华书局影印出版的《古今图书集成·历象汇编·历法典》第一百三卷《测量部·汇考四》收录《新法历书》一《大测》上和第一百四卷《测量部·汇考五》收录《新法历书》二《大测》下，称之为《古今图书集成》本(图6)[28]。

《古今图书集成》本版式分上、中、下三栏，每栏27行，每行20字，四周双边，黑口，单鱼尾，仅题“新法历书一”。次将《西洋新法历书》本“大测一卷”“大测二卷”改为“大测上”“大测下”，故在原书一卷、二卷之后，增“以上原本卷一”“以上原本卷二”双行小字作注。《古籍图书集成》本将编撰人员姓氏全部删除，其最大的变化在于重刊时，将明刻本的文字、格式以及一些可能存在歧义的地方进行改动。

2.5 《新法算书》本

乾隆朝编纂《四库全书》，子部·天文算法类收录《新法算书》一百卷，因避讳高宗，故易“历”为“算”，其中收有《大测》二卷，此为《新法算书》本[29]。《四库全书》从1773年(乾隆三十八年)开馆纂修，至1781年(乾隆四十六年)文渊阁藏本缮竣，1784年(乾隆四十九年十一月)，四部《四库全书》抄写完毕，装潢进呈，分贮文渊阁、文溯阁、文源阁、文津阁珍藏。1783年(乾隆四十七年)高宗下令续缮三份，分贮江南文宗阁、文汇阁和文澜阁珍藏。文津阁《四库全书》藏于中国国家图书馆，文溯阁《四库全书》现藏甘肃省图书馆，文澜阁《四库全书》则藏于浙江省图书馆。文渊阁《四库全书》原藏北京故宫，现藏台北故宫博物院[30]。

图7 《新法算书》文渊阁本

图8 《新法算书》文津阁本

图9 丁氏补抄本

1983年台湾商务印书馆将文渊阁《四库全书》影印出版，后上海古籍出版社又据该书影印出版了缩印本。2005年商务印书馆影印出版了文津阁《四库全书》。浙江省图书馆藏文澜阁《四库全书》也为公众提供查阅服务。三部《四库全书》中的《新法算书》卷九、卷十为《大测》一书，每卷署名“徐光启等撰”，将明刻本中“大测目录”改为“大测序”，并删除了目录后面的各卷篇名。但在《大测》具体内容上，《新法算书》文渊阁本(图7)[31]与《新法算书》文津阁本(图8)[32]略有差异，浙江图书馆藏文澜阁《四库全书》中的《大测》问题更多。《新法算书》文渊阁本和文津阁本并没有像《古今图书集成》本那样进行大范围的修改，这与《四库全书》纂修奖惩制度有关。四库全书馆制定了功过处分条例，分校、复校、总裁等各司其职，确保《四库全书》编纂质量[33]。但纂修人员还是更正了明刻本中的一个错误(详见下文)。相比而言，《新法算书》文津阁本质量好于文渊阁本，后者在抄录的过程中出现几处讹误。

浙江图书馆藏文澜阁《四库全书》中《大测》在用字、数字方面存在非常多的错误。文津阁本、文渊阁本更正的地方，文澜阁本依然保留[34]。据此可知浙江省图书馆藏《四库全书》中的《大测》并非是文澜阁原书。所以《大测》文澜阁本不复存在，浙江图书馆藏文澜阁《四库全书》中的《大测》，应是光绪年间丁丙(1832—1899)补抄而成[35]，当称之为丁氏补抄本(图9)。

据此可知《大测》主要的版本有《崇祯历书》本、《西洋新法历书》本、《新法历书》本，《古今图书集成》本、《新法算书》文渊阁本、《新法算书》文津阁本以及丁氏补抄本，而《新法算书》文澜阁本已经损毁。

3 版本递变分析

根据编纂《崇祯历书》的需要，邓玉函参照毕的斯克斯的《三角法》，并借用斯蒂文的《数学记录》部分内容翻译出中国第一部三角学著作《大测》。邓玉函在翻译时并没有按照《三角法》的内容一一对应翻译，而是根据中国已有数学知识结构和传统，将原书中的知识总结成“六宗”“三要”“二简法”“四根法”，由此构成《大测》主体知识。为了有助于中国历算学家的理解与接受和改历的需要，邓玉函略去《三角法》中大量的一般性解说，直接用简洁的语言和图形给出数学命题。原书常有“反之亦然”之说，即原命题的逆命题也成立。邓玉函或者将此句略去不译，或者将逆命题增列为新的命题。邓玉函还在编撰过程中增加了相当多的具体计算过程，采用《数学记录》第七题，就是以12°为例，给出所生成角度的正弦值。

因此，邓玉函并非严格意义上的翻译，而是根据需要进行编译。这与利玛窦(Matteo Ricci，1552—1610)的老师克拉维斯(Christopher Clavius，1538—1612)翻译拉丁语版《原本》(EuclidisElementorumlibriXV)类似。克拉维乌斯并未按照原书做出翻译，而是在他认为需要的地方对原文进行更改，这可以使原有的证明变得更加明白晓畅[36]。克拉维乌斯改编后的EuclidisElementorum前六卷被利玛窦和徐光启翻译为《几何原本》，1607年在中国出版。然而徐光启寄望《几何原本》“百年之后必人人习之”的局面并没有如期实现[37]。与此形成对比的是，邓玉函在《大测》中提出的以“六宗”“三要”“二简法”为纲的三角函数表造表程序，却成为清代造表法的主流模式。如《梅氏历算全书》中的《解八线割圆之根》、《御制数理精蕴》、戴震(1724—1777)的《勾股割圜记》以及安清翘(1759—1830)的《一线表》，无一不是依照《大测》的模式来讨论造表原理[38]。《大测》获得如此成功，与邓玉函等人的编译工作密不可分。从拉丁文底本到汉译本，是17世纪欧洲三角学传入中国的第一步，客观来看，这一步非常扎实。

《大测》从《崇祯历书》本到《西洋新法历书》本，发生了较大变化。这种变化并不仅仅体现在书名、编纂人等的改变，更重要的是更正了《崇祯历书》本中的2处数值错误。一处是在《大测》卷二“简法二”的示例中，《崇祯历书》本为“以半径为法，而一，得八七一五五七，即十五度弧之半弦。”《西洋新法历书》本更正为“五度弧之半弦”。另一处是在“简法二”之后，以12°为例介绍如何求所生成的各弧度正弦值时，《崇祯历书》本将34°30′正弦值误为35664062，《西洋新法历书》本改为正确数值5664062。如果说第二处错误是由于数值前面多出“三”这个衍字导致，比较容易判别。那么第一处错误则需要将前面计算过程看明白才能判断出正确弧度。

汤若望在重编《西洋新法历书》时工程量浩大，麾下众人虽各有分工，但每人负责的内容也十分庞杂。而《大测》的修订者能够更正这两个数值错误，实属不易。凭此一点，可知汤若望等人并非只改动《崇祯历书》的封面、校订各表的数据，还对理论性的历算部分，也尽可能去核对内容讹误。而南怀仁编纂《新法历书》时的条件要比汤若望时好很多，但仅仅更换封面书名，连首页上的“西洋新法历书”都没有替换，更没有继续校对《大测》书中其他错误。

由于《西洋新法历书》和《新法历书》都是在《崇祯历书》书版的基础上编纂，只能在个别地方进行剜改，无法对书中内容进行大范围改动。《古今图书集成》本继承了《西洋新法历书》本对《崇祯历书》本两处数值的更正，但却在明刻本基础上对原书内容重行刊刻出版，改变之处主要集中在以下三个方面：第一，将“于”“於”及“并”“幷”等前后不一的文字统一。第二，将明刻本中一些可能存在歧义的语句改动；如因明篇“论平面上三角形”第十一条，“对弧百二十度，倍于对角六十也”，《古今图书集成》本在“对角六十”后补一“度”字；又如明刻本为“得第四切线”，《古今图书集成》本在第四后补一“率”字，这可避免初学者阅读时产生疑惑。第三，打乱原书格式重新编排，这是《古今图书集成》本最大的特点。

在明刻本以及之后的《新法算书》本中，《大测》数学命题的解说、示例均较原题低一格同大字，而注为双行小字与前相连，格式较为统一。但《古今图书集成》本并没有严格遵从明刻本的格式，将有些例与题说相连。如表法篇“简法二”示例夹注，明刻本置于一段，《古今图书集成》本则将原书双行小字注文提行另起，而注后文字又提行另起，将一段完整的解说拆为三段，颇为不适。但《古今图书集成》本中也有个别格式改动是可取的。如因明篇“论平面上三角形”第三个命题后注文称：“《几何》六卷第五。此二题为大测之根本，不用开方，直以比例得之。法至简，用至大也。”明刻本为双行小字接上排。“此二题”指“论平面上三角形”第二、三条命题，故此注不应置于第三条注文之后。《古今图书集成》本将“此二题”一句提行另起，是合适的。

《古今图书集成》有着特定的编纂方法和目的，故对《大测》明刻本做了相当大程度的更改，个别改动犹可借鉴，整体却破坏了原书的结构，甚至存在多处随意删减乃至讹误之处。因此《古籍图书集成》本是清代诸版本中一个特例，《新法算书》本则又回归到明刻本的模样。

《新法算书》本中具体内容与格式，则严格遵从明刻本既定模式，除了保留《西洋新法历书》本中业已修订的两个正确数值，还更正了之前各版本都不曾发现的一处错误。《大测》卷二“简法一”次系示例中，有“丁壬离弧之正弦，即九度，与丁癸较等”一句。句中“九度”应为“十度”之误，明刻本均未能更正，而《新法算书》本改为“已壬”，为图形上十度所对应的弧。虽然拉丁文底本此处为10°，但《新法算书》本的改动也是正确的。《新法算书》本这个更正实属难得，若非对整个示例算法有清楚认识，是不可能发现并修改正确的，其难度更甚于之前《西洋新法历书》本更正两处数值错误。而丁氏补抄本此处与明刻本同误。

除此之外，《新法算书》文津阁本其他内容与明刻本完全相同，而《新法算书》文渊阁本则将表原篇“宗率五”“七十二度之弦”误抄为“七十二度之度”；将表法篇“要法三”例题中数值“五一七六三八〇”误抄为“五一七六三六〇”。可见《新法算书》文津阁本优于文渊阁本。

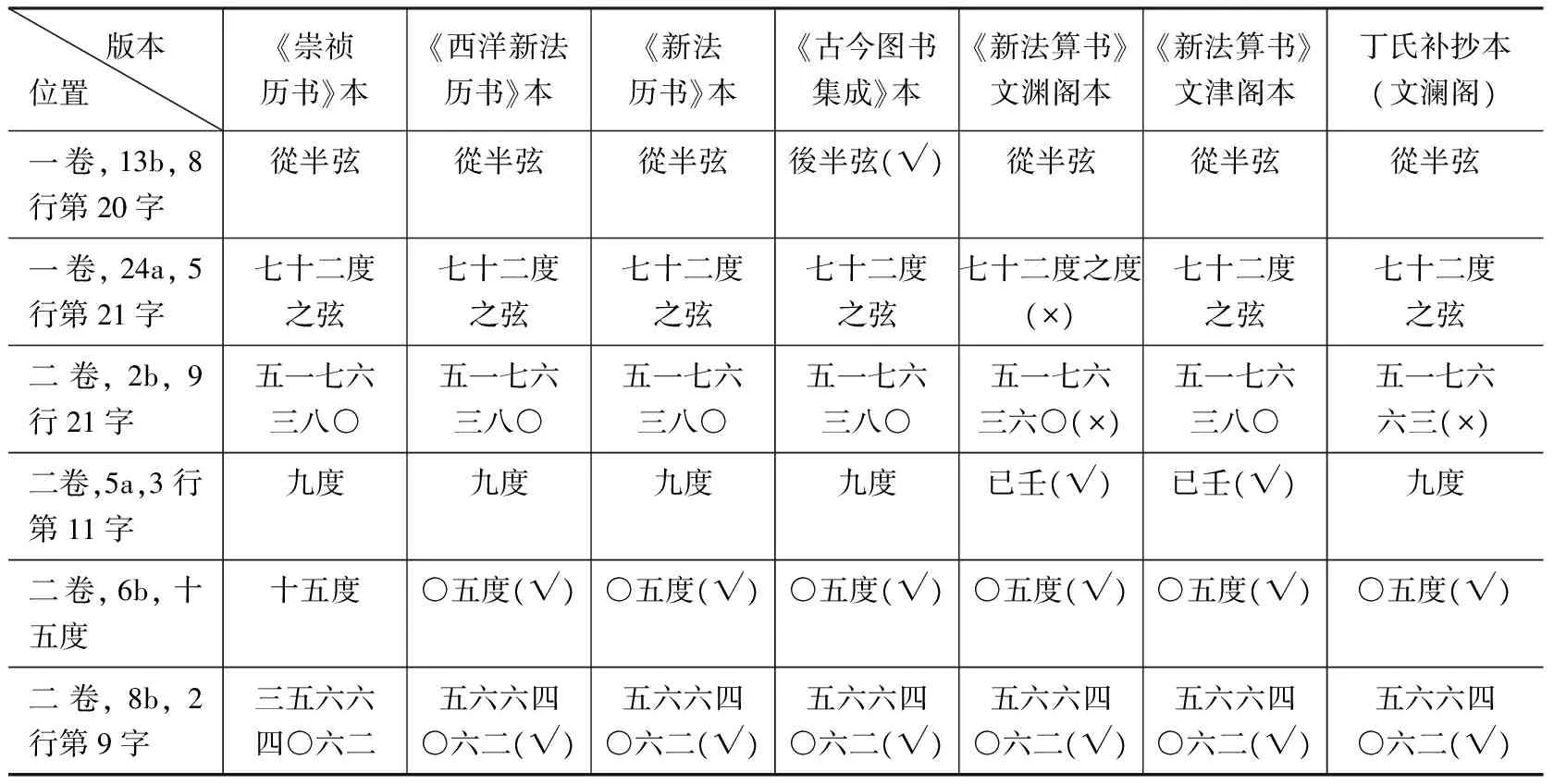
表1 《大测》诸版本内容变动一览表

(√)表示更正，(×)表示讹误

表1清晰地呈现历次修订《大测》的动态过程。从表1的统计中会发现两点：第一，除《新法历书》本和丁氏补抄本外，其他历次重修都对之前版本中的内容有所订正，无论是《西洋新法历书》本在数值上的更正，还是《古今图书集成》本、《新法算书》本对个别词语的修改，体现出编纂人员不但具有认真的工作态度，更重要的是还具备一定的数学素养；第二，编撰《新法算书》本时没有参考《古今图书集成》本，丁丙补抄文澜阁《四库全书》时也没有借鉴《古今图书集成》本和《新法算书》本。通过梳理《大测》诸版本可知，《崇祯历书》本成书最早，《西洋新法历书》本影响最大，《新法算书》文津阁本讹误最少。

4 从《大测》看《崇祯历书》的沿革

欧洲传教士为明末改历以及欧洲科学、技术知识传入中国做出了巨大的贡献，邓玉函即是其中代表人物。来华之前，邓玉函在欧洲已经是一位受人尊重的博学者，精通数学、哲学、神学等学科，与伽利略(Galileo Galilei，1564—1642)、法贝儿(Johannes Faber，1574—1629)、切西(Federo Cesi，1585—1630)等人相交往，并成为猞猁学院的成员[39]。正因为邓玉函对16—17世纪初欧洲科学发展有清楚的了解，他才选择在西方三角学发展史上具有重要里程碑意义的《三角法》(1612)一书作为底本，并加入当时欧洲最为重要的数学百科全书之一《数学记录》中若干具体计算过程来编译《大测》。《三角法》的作者毕的斯克斯与《数学记录》的作者斯蒂文皆为16—17世纪欧洲著名的数学家。邓玉函确实将当时西方最新、最重要的三角学成果传入中国。

在翻译过程中，邓玉函能够借鉴中国传统数学知识结构和思维模式对原著进行适当的改编，并增加大量具体案例，便于中国历算学家接受新知识，这是《大测》能够奠定清代三角函数造表法模式、西方三角学能够在中国顺利传播的可靠保障。徐光启的评价“邓玉函……历学专门，精深愽洽，臣等深所倚仗”[40]可谓中肯。

之后随着《崇祯历书》在清代的几度重刊，《大测》也从明刻明印本改为《西洋新法历书》本和《新法历书》本，之后又被重排为《古今图书集成》本，随后被重抄为《新法算书》本，晚清又被丁丙补抄。《三角法》和《数学记录》的某些内容传到中国并被编译为《大测》，以及《大测》诸版本的递变这一动态过程，客观展现了17世纪欧洲三角学著作在中国的发展脉络，亦也可视为《崇祯历书》编纂和沿革的缩影。可见《崇祯历书》每一次变动，并非之前认为仅根据政治因素更换书名、增减编纂人员那么简单，应有通晓历算学的编纂人员参与*石云里于2017年5月31日在“全球科技史视野下的中国与世界”国际学术研讨会上的报告“The Dissemination of Western Astronomy into China through the Chongzhen Reign Treatises on Calendrical Astronomy”也支持了这一结论。。他们在繁重的抄写、编纂过程中，尽可能对书中具体数学内容、计算过程与结果进行核准。

《崇祯历书》作为一部重要的中外科技文化交流文献丛书，学术界多有对其进行校勘整理的工作计划。而厘清丛书中每部译著的版本流传与底本来源信息，将会为校勘工作提供坚实的文献基础。如根据《大测》底本和诸版本情况，《崇祯历书》本虽成书最早，但错误较多，不适合作为校勘底本。《西洋新法历书》本成书较早，错讹较少，影响最大。《新法算书》文津阁本虽更正了《西洋新法历书》本中未曾发现的一个错误，质量最好，但这处更正并未参照拉丁文原本。故以《西洋新法历书》本作为底本，参照拉丁文原本及《几何原本》等其他典籍，对《大测》进行校勘，是科学的典籍整理方法。这对《崇祯历书》中其他历算学文献的校勘工作起到借鉴作用。

1 李迪. 中国历史上一次最大的天算引进项目[J]. 内蒙古师范大学学报(自然科学版), 2007,(6): 659—661.

2 朱家溍. 《崇祯历书》与《新法历书》[J]. 故宫博物院院刊. 1980,(4): 39—41.

3 朱家溍. 序《故宫藏珍本图书丛刊》[J]. 文物. 1998,(2): 80—86.

4 王渝生. 通玄教师汤若望[J]. 自然辩证法通讯, 1993, 15(2): 62—76.

5 江晓原. 《崇祯历书》的前前后后(下)[J]. 中国典籍与文化, 1997,(2): 112—116.

6 祝平一. 《崇祯历书》考[J]. 明代研究(11), 2008: 133—161.

7 Pingyi Chu, “Archiving Knowledge : A Life History of theChongzhenLishu(Calendrical Treatises of the Chongzhen Reign)”[J].Extrême-Orient,Extrême-Occident, 2007, 6: 159—184.

8 潘鼐. 前言[A]. 崇祯历书(上)[M]. 上海: 上海古籍出版社, 2009. 23.

9 李亮, 吕凌峰, 石云里. 被“遗漏”的交食——传教士对崇祯改历时期交食记录的选择性删除[J]. 中国科技史杂志, 2014, 35(3): 303—315.

10 (明)徐光启. 治历缘起[A]. 崇祯历书(下)[M]. 上海: 上海古籍出版社, 2009. 1560.

11 李俨. 三角术和三角函数表的东来[A]. 中算史论丛(3)[M]. 北京: 科学出版社, 1955. 191—253.

12 方豪. 中西交通史[M]. 长沙: 岳麓书社, 1987. 736.

13 严敦杰. 明清之际西方传入我国之历算记录[A]. 梅荣照主编. 明清数学史论文集[C]. 南京: 江苏教育出版社, 1990. 114—181.

14 白尚恕. 介绍我国第一部三角学——“大测”[J]. 数学通报, 1963,(2): 48—51, 封底.

15 Bartholomaeus Pitiscus.TrigonometriaeSiveDeDimensioneTriangulorumLibriQuinque.ItemProblematumVariorumNempeGeodaeticorum,Altimetricorum,Geographicorum,Astronomicorum:LibriDecem[M]. Augsburg, 1608 and 1612.

16 Hellmann, Martin. Pitiscus und seine kleine Trigonometrie[A]. In Michael Toepell (ed.).MathematikimWandel:Anregungenzueinemfächerübergreifendenmathematikunterricht[C], vol. 2 : 118—126. Hildesheim: Franzbecker, 2001.

17 Zeller, Mary Claudia.ThedevelopmentoftrigonometryfromRegiomontanustoPitiscus[D], Ann Arbor: University of Michigan doctoral dissertation, 1944. 102.

18 Sarton, George. Simon Stevin of Bruges (1548—1620)[J].Isis, 1934, 21(2): 241—303.

19 Simon Stevin.Hypomnematamathematica[M]. Lugdunum Batavorum, 1605—1608.

20 北京遣使会编. 北堂图书馆藏西文善本目录[M]. 北京: 国家图书馆出版社, 2009. 726, 841, 180—181.

21 (明)邓玉函. 大测[A]. (明)徐光启编纂, 潘鼐汇编. 崇祯历书(下)[M]. 上海: 上海古籍出版社, 2009.

22 潘鼐. 前言[A]. (明)徐光启编纂, 潘鼐汇编. 崇祯历书(上)[M]. 上海: 上海古籍出版社, 2009: 23.

23 徐宗泽. 明清间耶稣会士译著提要[M]. 上海: 上海书店出版社, 2006. 185—196.

24 (明)邓玉函撰,(清)汤若望订. 大测[A]. 故宫博物院编: 故宫珍本丛刊, 第三八七册《西洋新法历书》(五)[M]. 海口: 海南出版社, 2000年.

25 (明)邓玉函撰,(清)南怀仁订. 大测[A]. 新法历书[M]. 台北故宫博物院图书文献馆藏. 故殿006504号.

26 (清)刘铎. 古今算学丛书. 天文第七[M]. 上海: 算学书局, 光绪二十四年(1898)据微波榭本等石印. 16.

27 赵长海. 《古今图书集成》版本考[J]. 古籍整理研究学刊, 2004,(3): 43—47.

28 (明)邓玉函. 大测[A]. 古今图书集成·历象汇编历法典[M]. 上海: 中华书局, 中华民国二十三年(1934).

29 (清)纪昀. 四库全书总目(四)[M]. 台北: 艺文印书馆, 1964. 2089.

30 陈祖武, 朱彤窗. 乾嘉学派研究. [M] 石家庄: 河北人民出版社, 2005. 29—34.

31 (明)徐光启, 邓玉函等撰. 大测[A]. 文渊阁《四库全书》. 七八八册[M]. 上海: 上海古籍出版社, 1987.

32 (明)徐光启, 邓玉函等撰. 大测[A]. 文津阁《四库全书》. 七八九册[M]. 北京: 商务印书馆, 2005.

33 陈清慧, 董馥荣. 编修《四库全书》奖惩办法管窥[J]. 文献, 2006,(4): 159—168.

34 (明)徐光启, 邓玉函等撰. 大测. 丁氏补抄文澜阁《四库全书》[M]. 浙江省图书馆藏, 清光绪八年至十四年. 善专号575.

35 童正伦. 丁氏补抄文澜阁四库全书述评[J]. 图书馆研究与工作, 2011,(4): 66—70.

36 Thomas L Heath.TheThirteenBooksofEuclid’sElements[M]. New York: Dover Publications, 1956. 105.

37 刘钝. 从徐光启到李善兰——以《几何原本》之完璧透视明清文化[J]. 自然辩证法通讯, 1989, 11(3): 55—80.

38 Jiang-Ping Jeff Chen. Trigonometric tables: explicating their construction principles in China[J].ArchiveforHistoryofExactSciences, 2016, 69(5): 491—536.

39 埃利希·蔡特尔著. 孙静远译. 邓玉函, 一位德国科学家、传教士[A]. 载张西平主编. 国际汉学(二十二辑)[M]. 郑州: 大象出版社, 2012. 38—87.

40 (明)徐光启. 治历缘起[A]. (明)徐光启编纂. 潘鼐汇编. 《崇祯历书》(下)[M]. 上海: 上海古籍出版社, 2009. 1569.

On the European Sources and Various Editions ofDace(Grand Measure)， the First Trigonometric Treatise in China

DONG Jie1，Jiang-Ping Jeff CHEN2

(1.InstitutefortheHistoryofScienceandTechnology，InnerMongoliaNormalUniversity，Hohhot010022，China； 2.DepartmentofMathematicsandStatistics，St.CloudStateUniversity，Minnesota，St.Cloud，MN56301，USA)

Chongzhenlishu(Astronomical Compendium during the Chongzhen Reign) as the largest translation/compilation project of a scientific compendium in Chinese history and the main efforts of the Calendar Reform put forth by the Ming China (1368—1644) shortly before its fall has attracted the attentions of many historians.Dace(Grand Measure)， the first trigonometric treatise in China， was part of this project. This paper clarifies the European sources ofDaceand examines its various editions in the 17—19thcentury， documenting the editions’ differences. Based on the earlier identification in the literature， we also compareDacewith various European trigonometric treatises in the early 17th century. We conclude that Johann Terrenz composed/compiledDaceby translating parts of BartholomaeusPitiscus’s 1612 edition ofTrigonometriaeand Simon Stevin’s 1608 Latin edition ofHypomnematamathematicaor its French translation，Mémoiresmathématiqves.The technical content was translated and presented in the manner similar to that employed by Chinese scholars so as to reach wider readership and acceptance. It is evident that Johann Terrenz introduced into China many of the most advanced and important trigonometric results in the early 17th century， cherry-picking and modifying the content to suit his purpose. Its approach to construct trigonometric tables became paradigmatic， followed by most trigonometric treatises in the 17th， 18th， and 19thcentury. The findings of this paper also establish that the edition ofDaceinXiyangxinfalishu(Astronomical Compendium according to the New Methods from the Western Ocean) offers the best quality to serve as the foundation for further collation ofDace， being the second earliest and among the ones with fewest mistakes. To this paper demonstrates a concrete model for future investigations ofChongzhenlishu.

Grand Measure， Trigonometry， Chongzhenlishu

2016- 12- 31；

2017- 04- 25

董杰，1982年生，内蒙古呼和浩特人，博士，内蒙古师范大学科学技术史研究院副教授，研究方向为清代数学史研究，Email: djnmdongjie@126.com；陈建平，1966年生，博士，美国明尼苏达州州立大学圣克劳德分校数学统计系教授，研究方向为中国数学史。

国家高层次人才特殊支持计划(编号：W02070347)；霍英东基金会青年教师基金(编号：151098)。

N092

A

1673- 1441(2017)02- 0173- 13