基于量子粒子群优化算法的多机协同目标分配问题研究

王记丰李峥叶文

（1.中国船舶工业系统工程研究院北京100094）（2.海军航空工程学院兵器科学与技术系烟台264001）

基于量子粒子群优化算法的多机协同目标分配问题研究

王记丰1李峥1叶文2

（1.中国船舶工业系统工程研究院北京100094）（2.海军航空工程学院兵器科学与技术系烟台264001）

针对粒子群优化算法易陷入局部极值、搜索空间有限等不足，将量子理论与粒子群优化算法相结合，采用量子粒子群优化算法来解决于多机协同目标分配问题。量子粒子群优化算法中的粒子采用向量表示，该向量由多机协同目标分配问题中的每个分配方案组成，由此在解空间内搜索最优解。仿真表明，该算法收敛速度快、全局收敛性能好，更加适合于目标分配问题求解。

多机协同；目标分配；粒子群算法；量子粒子群算法

Class NumberTP301.6

1 引言

多机协同目标分配问题就是在综合考虑多种约束条件下，对攻击的目标进行合理分配，确保飞机编队以最小代价获取最大攻击效果。多机协同目标分配问题的实质是进行组合优化，常用的方法主要有精确搜索和启发式搜索两种，前者主要是穷举搜索法，后者主要有遗传算法和禁忌搜索等。但是这些方法都存在巨大的计算代价，这也是组合优化问题急需解决的难点问题。

目前，粒子群优化算法（particle swarm optimi⁃zation，PSO）与经典的启发式搜索算法相比，具有较大的优势和可行性。但在应用过程中，PSO算法也会经常出现早熟现象［1～2］。针对这些不足，本文将粒子的量子行为引入到粒子群算法当中，并采用其来解决多机协同目标分配问题，该算法比PSO算法具有更好的全局搜索能力，能够有效地避免PSO算法陷入局部最优解，提高了算法的收敛速度。

2 问题描述

假设Vi（Vi∈V，i=1，2，…，NV）表示飞机，Ti(Ti∈T，i=1，2，…，NT)表示目标，Pi(Pi∈P，i=1，2，…，NP)表示威胁或者禁飞区。设集合

集合，则多机协同目标分配就是在要求的时间内将所有目标分配给各架飞机，即

并且满足整体作战效能最大，如图1所示。

多机协同目标分配的最优目标是多架飞机的整体作战效能最大，其评价指标主要有飞机的损耗程度、目标的价值收益和飞行航程的长度［3～4］。所以，将飞机损耗最小、目标价值收益最大、飞行航程最短作为衡量多机协同目标分配方案优劣的重要性能指标。

1）飞机损耗最小指标

该指标主要是引导目标分配方案向着减小飞机自身损耗的方向搜索，使飞机所受的威胁度最小，趋向于在安全航路飞行。假设飞机u攻击目标i的生存概率为PSi，则飞机攻击该目标时的损耗为HSi=1-PSi。因此，在进行目标分配时，尽量使得所有飞机的损耗之和最小，即

2）目标价值收益最大指标

该指标主要是引导目标分配方案向着飞机作战效能最大化的方向搜索，使飞机尽量攻击价值高的目标。假设飞机u攻击目标i的杀伤概率为PKi，目标i的价值为vi，则目标价值收益为Vi=vi·PKi。因此，在进行目标分配时，尽量使得总收益最大，即

3）飞行航程最短指标

该指标主要是引导目标分配方案向各个飞机近距离任务目标进行搜索。假设飞机u与目标i间的距离为Di，则在进行目标分配时，尽量使得总航程最小，即：

综上所述，多机协同目标分配的性能指标函数为

其中，ω1，ω2，ω3为加权系数。

3 量子粒子群目标分配算法

在粒子群优化算法中，主要是通过粒子的运动来搜索，而粒子的运动由速度和位置来决定，并且具有一定的轨迹和满足一定的规律。因此，在传统粒子群算法搜索过程中，存在不能搜索整个可行空间的可能，达不到全局收敛，易陷入局部最优［5］。

孙俊根据量子力学理论对粒子群优化算法进行了改进，提出了新的算法，这种算法被命名为量子粒子群优化算法［6～8］。该算法将量子的行为应用于粒子的运动，用波函数来确定粒子的状态，将整个解可行空间作为量子空间，粒子在量子空间中进行搜索，从而避免算法陷入局部极值，提高算法的全局搜索能力。

3.1 量子粒子群优化算法数学模型

在传统的PSO算法中，粒子的位置和速度共同决定了粒子的运行轨迹，粒子沿着确定的轨迹运动。但是，根据量子力学理论和不确定性原理，轨迹是没有意义的，粒子的位置和速度是无法同时确定的。因此，如果将量子行为作用于PSO中的粒子，那么，PSO算法的工作方式将是不一样的。孙俊等人给出了量子粒子群优化算法。该算法描述如下：

在量子粒子群优化算法中，用波函数来确定粒子的状态，整个解可行空间作为量子空间，粒子在整个量子空间中进行搜索，从而提高算法的全局搜索能力［9］。因此，可以根据薛定愕方程得到的粒子出现的概率密度来表示粒子在量子空间中的位置，即粒子的随机位置方程为

式中u为［0，l］区间的随机数，并且服从均匀分布，L由下式确定：

QPSO算法的进化方程：其中i=1，2，…，m；d=1，2，…，D；u、r1和r2为［0，1］区间的随机数；t为当前算法搜索的迭代次数；粒子的维数为D，种群数目为M，u和p是为［0，l］区间的随机数，Pi(t)表示粒子的当前最佳位置，Pg(t)表示粒子的全局最佳位置，mbest(t)表示群体中平均最佳位置，pid(t)为Pi(t)和Pg(t)之间的随机点。β为该算法中唯一的一个重要参数，即收缩扩张系数，其值具有多种设置方法，可以为固定值，也可为变值，如按递增或递减的方式变化，在通常情况下一般采用下式来进行该参数的取值：

β随着迭代线性地从m递减到n，通常m=1，n=0.5，式中MaxTimes是迭代的最大次数。当β≤0.5时，式中采用减号；当β＞0.5时，式中采用加号。

3.2 量子粒子群优化算法流程

步骤1：进行群体规模、迭代次数、种群个数、维数的初始化；

步骤2：计算各自粒子的最好位置，得到Pi和Pg；

步骤3：优化过程，按照量子粒子群算法的进化方程更新QPSO算法中的所有粒子；

步骤4：计算粒子位置，进行局部极值和全局极值的更新，即更新Pi和Pg；

步骤5：搜索结果是否满足要求判断，满足则停止搜索并输出最优解，不满足则跳到步骤3继续搜索。

QPSO算法描述如下：

初始化所有粒子的位置向量，记录个体极值和全局极值

4 基于量子粒子群算法的多机协同目标分配

4.1 粒子的编码

QPSO本质上是连续的，因此在将QPSO应用于目标分配问题求解中，需要将连续解映射到离散解上，本文采用直接取整法的整数规格化方法来对粒子位置参数处理。直接取整法就是在搜素迭代过程中，直接将各粒子的位置参数值取整处理，来满足目标分配离散问题求解的需要。

采用自然数编码进行粒子的编码，将目标的总数作为粒子向量的长度，各粒子位置向量的各个分量为对应的各个目标被分配的相应飞机序号。比如，飞机数目n为8，目标数目m为15，一个粒子为

即X=[3 7 8 4 7 2 6 7 1 8 5 5 2 4 3]表示为粒子的位置向量，具体含义为第3架飞机攻击第1个目标，第7架飞机攻击第2个目标，…，第4架飞机攻击第14个目标，第3架飞机攻击第15个目标。同时，粒子的位置向量还要满足一定岳苏条件，如每一个目标必须分配一个飞机的限制，单位粒子取值范围为[1，n]，以及飞机的最大攻击目标数目限制，即单架飞机攻击的目标总数不能超过其最大攻击能力。

4.2 初始粒子群的确定

在该算法中，一个可行的分配方案就可用一个粒子表示，即对应于一个一维数组。为了确保粒子群在初始状态有比较好的分散度，对于每一个目标，随机的在［1，n］中选择一架飞机分配给该目标，如果随机选择的飞机已经达到其最大攻击目标数，则重新生成随机数选择其它飞机来分配给该目标，形成一个可行解。根据同样的规则，构造一定数量的初始粒子，形成初始粒子群。

算法的运行效率和效果在一定程度上还受粒子个数M的影响，粒子个数M过小时，有利于提高算法运行速度，但易陷入局部极值，即早熟收敛；粒子个数M过大时，则会降低算法的运行效率。一般M取值为30-60之间为宜，本文中取M=30。

4.3 适应度函数值的计算

根据衡量多机协同目标分配方案优劣的性能指标，即飞机损耗最小、目标价值收益最大、飞行航程最短，多机协同目标分配的适应度函数可确定为

其中，ω1，ω2，ω3为权系数。在本文的仿真实例中，主要是为了验证协同目标分配算法的有效性，因此简化了协同目标适应度函数，主要考虑以目标价值收益程度来指导目标分配，即权系数为ω1=1，ω2=0，ω3=0。

4.4 量子粒子群算法的流程设计

由于量子粒子群算法的进化方程是针对连续域中的问题求解来进行设计的，但是多机协同目标分配问题是离散域中的问题，因此，直接利用量子粒子群算法的进化方程进行粒子位置的更新，效果不是很理想。针对多机协同目标分配问题的特点，重新设计了量子粒子群算法的进化方程。

1）mbest(t)的计算

针对群体中平均最佳位置mbest(t)，不是进行直接的数值求平均方法来计算，而是通过粒子位置向量中每位上数值出现的频率来计算，即某t时刻，假设群体中有m个粒子，将所有粒子位置向量的第i位数值取出进行比较，其中出现频率最多的数值赋值于mbest(t)的第i位，即将m个粒子位置向量中在第i位上出现频率最多的数值设定为群体中平均最佳位置mbest(t)的第i位数值。这样，通过每一位数值出现频率的比较，最终得到mbest(t)。

2）pid的计算

pid为Pi和Pg之间的随机点，在量子粒子群算法的进化方程中，pid的计算公式也是针对连续域中的问题来进行设计的，因此，这里我们也进行了改进。针对pid中的每j位，通过随机生成一个［0，1］的随机数，当rand(0，1)≤0.5，则pid(j)= Pid(j)，当rand(0，1)＞0.5，则pid(j)=Pgd(j)。

3）Xid(t+1)的更新

Xid(t+1)的更新正常按照量子粒子群算法的进化方程进行更新，只是在每次更新完毕之后，采用直接取整法，将各粒子的位置参数值取整，计算其适应值，并提取Pi、mbest和Pg，接着计算下一个位置，进入下一次取整，直到满足计算要求。

应用量子粒子群算法进行多机协同目标分配的流程描述如下：

（1）初始化粒子群，确定各粒子初始的随机位置，同时计算Pi和Pg；

（2）动态调整收缩扩张系数；

（3）各粒子适应度函数值的计算；

（4）对于每个粒子，比较其适应值与当前pi(t)的适应值，若较好，则更新Pi(t)；比较其适应值与当前Pg(t)的适应值，若较好，则更新Pg(t)；

（5）算法收敛判断，如满足，则输出Pg(t)，算法结束；否则，执行（6）；

（6）根据量子粒子群算法的进化方程生成新的粒子，转到步骤（2）；

（7）输出最佳分配方案作为优化结果，算法结束。

5 仿真验证与分析

算例：8架无人机编队对15目标协同目标分配

假设有8架无人机编队和15个地面目标。采用表1中数据作为目标的价值、飞机对目标的杀伤概率。

根据这一想定，对上述问题分别采用遗传算法、离散粒子群算法和量子粒子群算法进行仿真，并对比分析仿真结果。遗传算法、离散粒子群算法和量子粒子群算法在60次迭代过程中最好解、平均解和最差解的变化曲线如图2～图4所示，仿真结果比较分析如图5和表2所示。

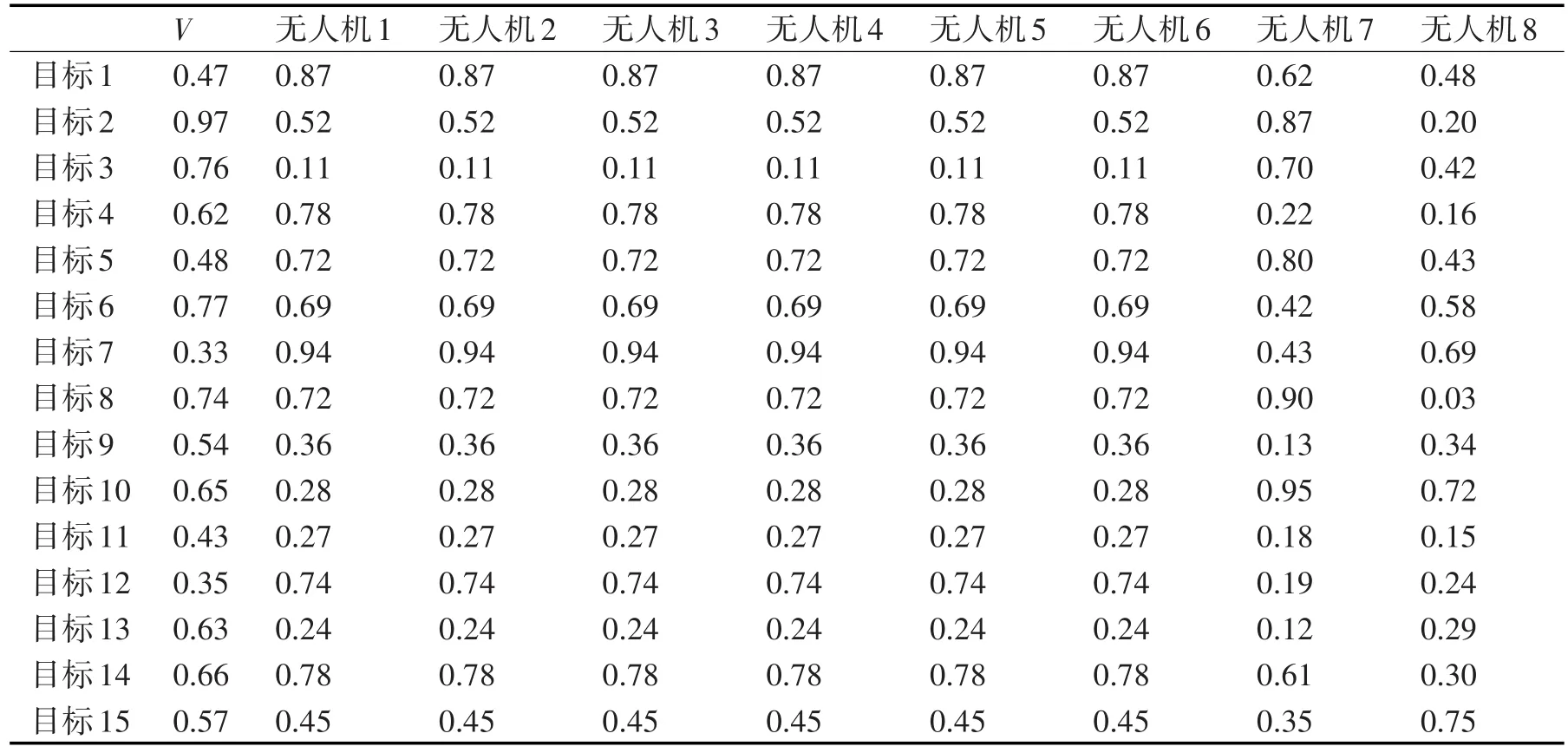
表1 目标分配初始数据

表2 算法性能比较

从图2～图4的各种算法收敛速度和解的性能可以看出，相对于遗传算法和离散粒子群算法，量子粒子群算法具有较好的收敛特性，可以较快地搜索到问题的最优解。此外，量子粒子群算法的优化效率也较高，能够在较少的进化代数内，其解群就向最优解的方向收敛。

6 结语

本文针对粒子群优化算法搜索空间有限、容易陷入局部最优点的缺陷，应用基于量子行为的粒子群优化算法解决多机协同目标分配问题。通过自然数编码，每个粒子表示一种可能的分配方案，由此在解空间内搜索最优解。实例仿真结果表明，该算法能够有效解决多机协同目标分配问题。

［1］叶媛媛，多UCAV协同任务规划方法研究［D］长沙：国防科学技术大学，2005.

［2］龙涛，多UCAV协同任务控制中分布式任务分配与任务协调技术研究［D］长沙：国防科学技术大学，2006.

［3］叶文，朱爱红，欧阳中辉，范洪达.基于混合离散粒子群算法的多无人作战飞机协同目标分配［J］.兵工学报，2010，03：331-336.

［4］叶文，朱爱红，潘长鹏，范洪达.多UCAV协同目标分配算法研究［J］.系统工程与电子技术，2010，01：104-108.

［5］潘全科，王文宏，朱剑英.解决无等待流水车间调度问题的离散粒子群优化算法［J］.计算机集成制造系统. 2007.13（6）：1127-1132.

［6］周翠华.量子粒子群优化算法的研究及应用［D］.大庆：东北石油大学，2011.

［7］SUN Jun，FENG Bin，XU Wen-bo.Particle swarm opti⁃mization with particles having quantum behavior［C］// Proc of Congress on Evolutionary Computation.2004：325-331.

［8］SUN Jun，XU Wen-bo，FENG Bin.A global search strate⁃gy of quantum behaved particle swarm optimization［C］// Proc of IEEE Conference on Cybernetics and Intelligent Systems.2004：111-116.

［9］张兰.量子粒子群算法及其应用［D］.西安：西北大学2010：25-40.

Multi-plane Cooperation Task Assignment Problem Based on Quantum-behaved Particle Swarm Optimization Algorithm

WANG Jifeng1LI Zheng1YE Wen2
（1.Systems Engineering Research Institute，Beijing100094）（2.Department of Ordnance Science and Technology，Naval Aeronautical Engineering Institute，Yantai264001）

multi-plane cooperation，task assignment，particle swarm optimization，quantum-behaved particle swarm opti⁃mization

TP301.6

10.3969/j.issn.1672-9730.2017.08.008

2017年2月3日，

2017年3月18日

航空科学基金（编号：20111784002）项目资助。

王记丰，男，硕士，高级工程师，研究方向：任务规划技术、指挥自动化。李峥，男，硕士，高级工程师，研究方向：任务规划技术，指挥自动化。叶文，男，博士，高级工程师，研究方向：作务规划技术、航空军械。

AbstraetCoping with such disadvantages of particle swarm optimization algorithm as finite sampling space，being easy to run into local optima，quantum-behaved particle swarm optimization is used to be solve the multi-plane cooperation task assign⁃ment problem.A vector composed of every assignment regarded as a particle in this algorithm to evolve.Then，the sampling space is searched for the global optima.The simulation results show that the algorithm has better global convergence ability and more rapid convergence，and it is superior to genetic algorithm and particle swarm optimization algorithm，and the proposed algorithm is effec⁃tive and feasible.