四不等跨连续梁振动试验分析及冲击系数探讨

任张晨, 袁向荣, 陈泽贤, 董湘婉

(广州大学 土木工程学院， 广州 510006)

四不等跨连续梁振动试验分析及冲击系数探讨

任张晨, 袁向荣, 陈泽贤, 董湘婉

(广州大学 土木工程学院， 广州 510006)

分别讨论并比较在不同跨径比下的连续梁的固有频率及振型的变化规律和异同点。试验梁采用槽型梁，除了对模型进行固有振动分析和理论计算外，还采用有限元软件分别对各个跨径比下的试验模型进行有限元计算分析和计算。以有限元的计算结果作为参考，同传统检测试验得到的结果进行对比分析，论证振型变化规律的真实性。结果表明：对于不同跨径的对称四跨连续梁，支座对称移动时，前3阶振型始终对于中支座是对称或者反对称的，并且中支座在2阶振型中首先出现反弯点。当计算跨中正弯矩效应时，冲击系数按照《桥规》采用基频计算；当计算中支座负弯矩效应时，冲击系数应采用第2阶频率进行计算。

四不等跨连续梁； 模态分析； 振动分析； 冲击系数

0 引 言

连续梁桥作为一种常见的桥梁结构形式，在现代城市桥梁和道路建设中得到广泛的应用。在使用过程中，由于车辆在过桥时对桥梁结构产生的冲击，《公路桥涵设计通用规范》[1](JTG D60-2004，以下简称《桥规》)4.3.2条规定，采用桥梁基频的函数来计算冲击系数汽车荷载的冲击力标准值为汽车荷载标准值乘以冲击系数μ来研究汽车过桥时的动力影响[2]。我国《桥规》第五款规定：当f<1.5 Hz时，μ=0.05； 当1.5 Hz≤f≤14 Hz时，μ=0.176 7 lnf-0.015 7；当f>14 Hz时，μ=0.45；式中,f为结构基频。

然而冲击系数需要考虑到其他复杂因素的影响[3]，例如桥梁和车辆本身的振动特性，车辆的行驶过程，路面情况等。对于冲击系数的研究最早可以追溯到19世纪，在接近200年的时间内，冲击系数不断在被改写。对冲击系数的研究实验，车桥耦合振动试验[4-5]最为常见。漆景星等[6-7]指出，《桥规》的冲击系数的规范值偏小。该现象在连续梁中支座位置处的表现尤为明显，仅仅单一的选取基频作为冲击系数的计算依据是远远不够的。所以对连续梁桥进行完备的模态分析[8-10]是至关重要的。目前的连续梁桥的模态分析也较为成熟，胡邦义等[11-12]对四、五等跨连续梁也进行了研究。但是在不同跨径比下的四跨连续梁并没有进行模态分析研究。本文进一步探究在跨径比下的四跨连续梁的模态试验，讨论冲击系数的计算选取[13]，为以后的桥梁振动特性研究[14]提供一定的参考。

1 四跨连续梁的固有振动分析

实际生活中，大多连续梁均是不等跨、不等截面，因此为了排除其他因素的影响，试验采取等截面来论证连续梁桥的固有振动特性。如图1所示，描述了四跨连续梁桥的一般情形，根据Euler-Bernoulli理论。第S跨的第n阶的振型函数为：

φns(x)=Anssinαnsx+Bnscosαnsx+Cnssinhαnsx+Dnscoshαnsx

图1 四跨连续梁的一般模型

根据边界条件可推导出四跨连续梁的固有振动频率为：

对应的前3阶振型图见图2。

随后建立四等跨的有限元模型，试验梁的弹性模量E=70 GPa，泊松比μ=0.3，线性膨胀系数α=1.2×10-5/°C,横截面积A=96 mm2,梁总长5.6 m，容重Dens=28 kN/m3,截面图如图3所示。

将有限元计算分析结果同精确计算结果相比较，如表1所示。由于计算过程的近似取值，所以有限元计算结果和理论值存在一定误差，但是误差均不大于7%，在允许误差以内。因此有限元计算是较为真实可靠的。

图2 四跨连续梁的前3阶振型

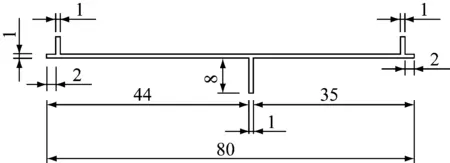
图3 试验梁横截面图(mm)

2 不同跨径比的对称四跨连续梁有限元模态分析

图4所示为实验梁的试验模型的起始位置，即四等跨的位置。梁总长5.6 m，将其4等分，一共设有5个支座，从左到右编号分别为1～5，支座1设置X，Y，Z方向的约束，其他支座只设置Z方向上的约束。支座2～4分别在连续梁的3个四等分点上。为了研究不用跨径比下的连续梁的振型和频率，因此固定支座1，支座3和支座5的位置，只同时移动支座2和支座4。移动方向为向内移动和向外移动，移动的距离分为10、20和30 cm。

图4 有限元四等跨模型图(mm)

为了保持一致性，即试验条件和传统加速度传感器检测法一致，有限元建立模型时，在每跨2个3等分点处均施加1个集中力，用来代替加速度传感器的重力，即F=G=1.4 N。不同跨径比下的对称四跨连续梁的前3阶频率见表2，前3阶振型见图5。

(a) 1阶

(b) 2阶

(c) 3阶

图5 有限元计算的不同跨径下的阵型图

3 传统检测法的模态分析试验

3.1 传统检测试验模型

试验梁总长5.6 m，首先将试验梁布置成四等跨，支承方式均钢辊轴，支座1采用砝码压重约束构成固定支座，其他支座采用直径2.5 cm钢管形成活动支座。在每跨的2个2/3点均放上加速度传感器(试验选用BI1148型加速度传感器)。将传感器与INY306U信号采集分析仪接通后，并将仪器连接上计算机，然后对试验梁进行锤击，便可以采集并记录整个过程的振动信号，试验模型简图见图6。之后和有限元的模型一致，支座1，3，5固定不动，只同时移动支座2和4，移动距离分别为10、20和30 cm，移动方向同样分为内移和外移，即一共采集到7组不同跨径的四跨连续梁的振动信号。

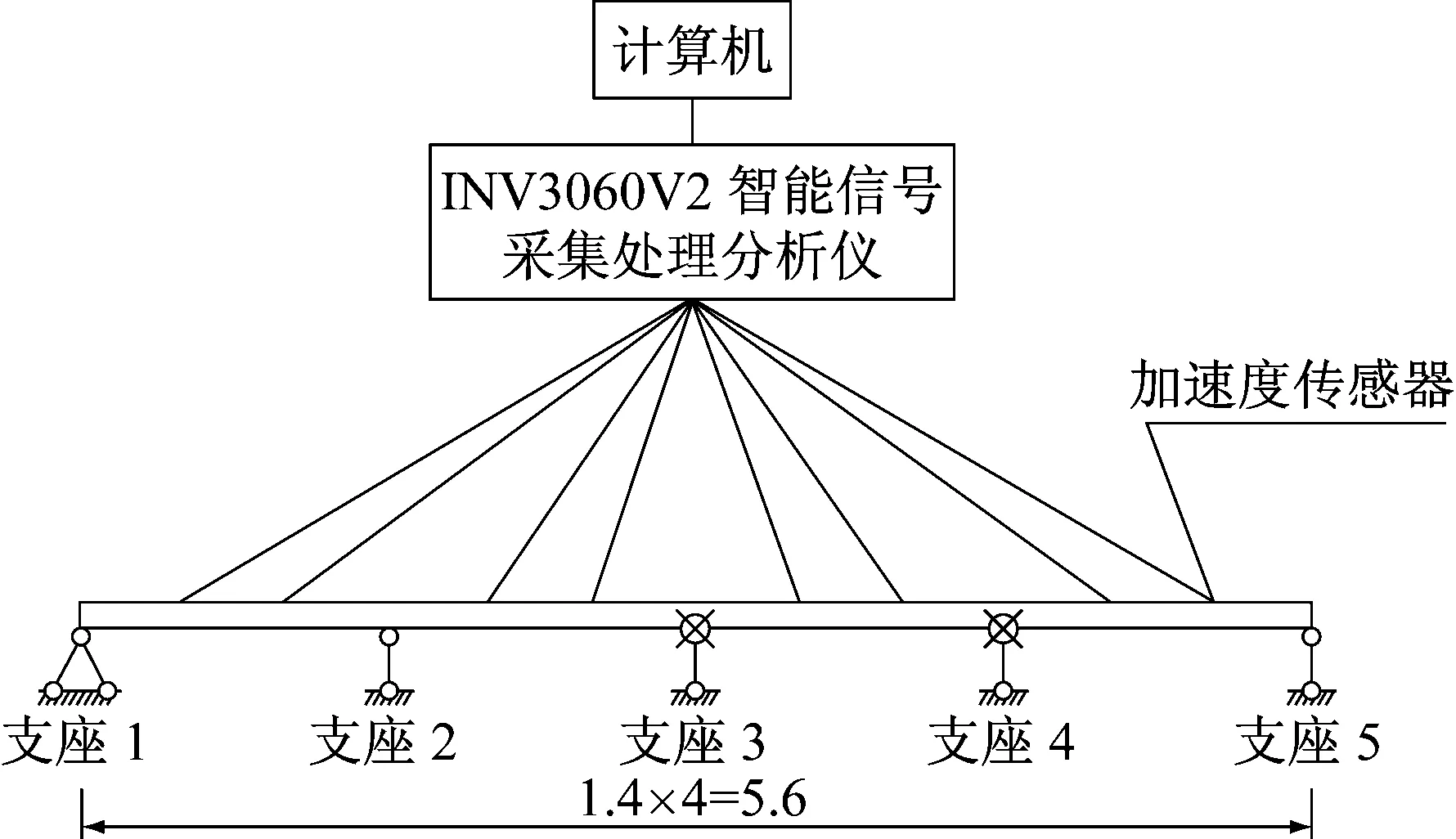
图6 试验模型简图(m)

3.2 传统检测试验结果

对7组不同跨径比下实验梁的振动信号导入模态分析系统[15]进行模态分析，得到前3阶频率见表3，前3阶振型见图7(每阶阵型图中的顺序和频率表中跨径组合顺序对应)。

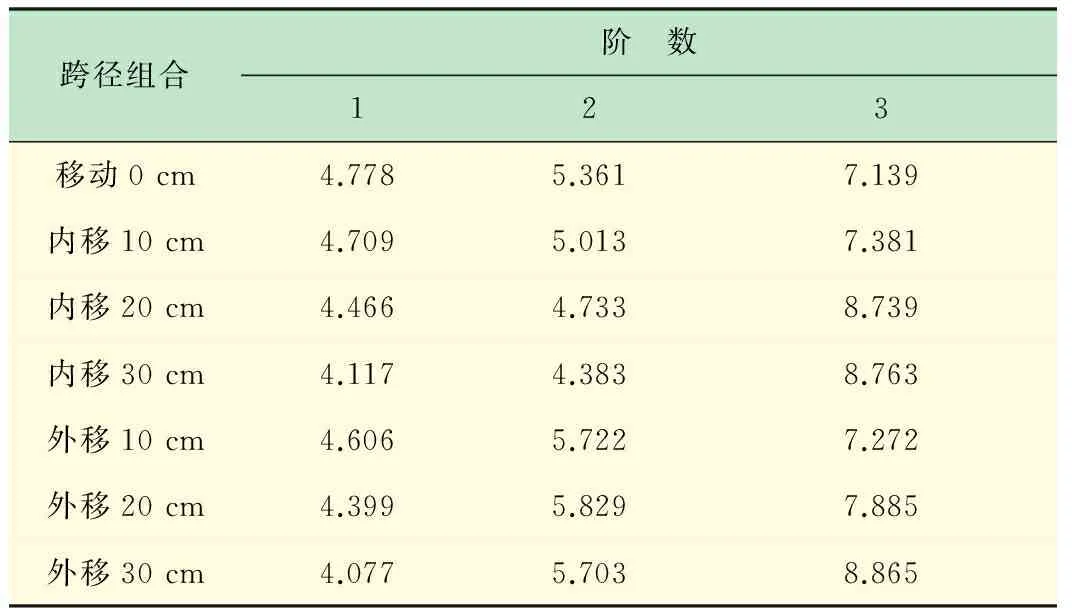
表3 传统检测的前3阶频率表 Hz

4 结果对比分析

以有限元的计算结果为标准，对前3阶频率，将有限元模态分析结果和传统加速度传感器检测结果的进行误差计算，得到的误差汇总至表4。结果表明：最小误差仅为0.35%，最大误差为5.35%，总体来看1阶频率的误差平均最小，2阶其次，3阶频率的误差最大。

由于激励能量较小，故在传统检测中对高阶的模态分析会影响稍大些，所以第3阶频率的误差比2阶稍大，但所有误差均在6%以内，也证明了不同跨径比下的四跨连续梁的前3阶频率变化是真实的。

有限元模态分析得到的不同跨径比下的不同跨径四跨连续梁的前3阶振型和由传统检测模态分析得到的前3阶阵型图基本吻合。

1阶振型中，7组模型均是关于支座3正对称，整个波形是一个完整的正弦波，且关于支座3反对称。

(a) 1阶

(b) 2阶

(c) 3阶

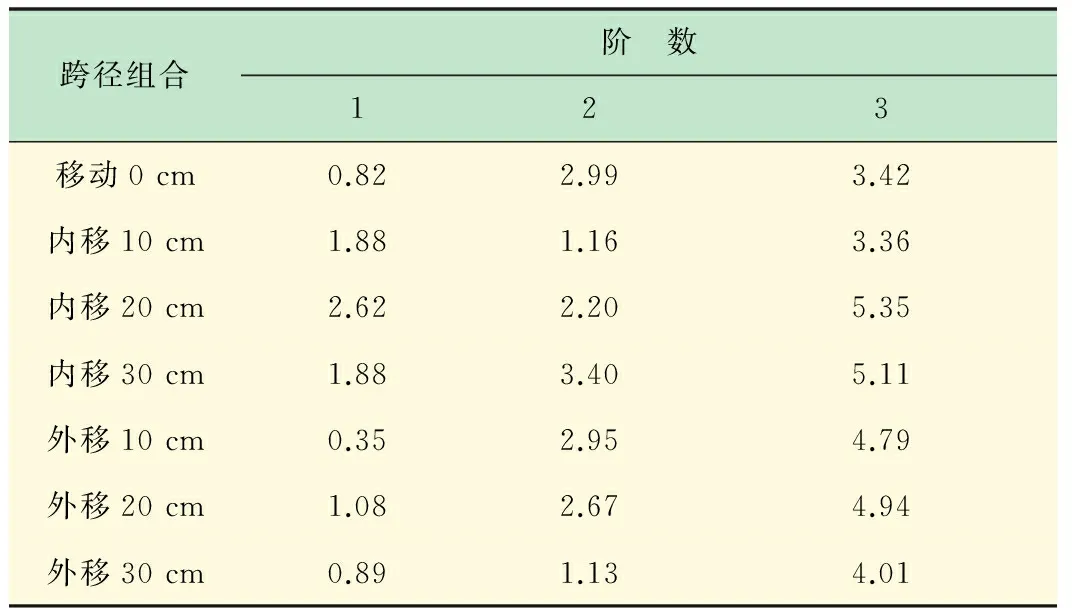
图7 实测的不同跨径下的阵型图

随着支座2和支座4的内移或外移，跨径变小的两跨的正弦波的幅值减小，跨径变大的两跨的幅值增大。但1阶振型的整体趋势没有本质的变化。

2阶振型中，所有7组不同跨径比的2阶振型均关于支座3正对称，每跨都是半个正弦波，且无论内移或者外移，跨径较大的两跨幅值比跨径小的两跨辅助要大，并且支座3处始终是反弯点，每跨幅值最大点均在每跨跨中位置。

3阶振型中，所有7组不同跨径比的3阶振均关于支座3反对称。当四等跨连续梁时，每跨均是半个正弦波，支座2和支座4处是反弯点，随着支座2和支座4的内移，反弯点在支座2之前和支座4之后，并且第一跨和第四跨由半个正弦波变成一个完整的正弦波。第2、第3跨保持半个正弦波不变，且跨中曲率在逐渐增大。外移反弯点则出现在支座2之后和支座4之前，第2、第3跨则是由半个正弦波变成一个完整的正弦波，第1、第4跨仍保持半个正弦波，且随着支座的外移，第1、第4跨跨中位置的曲率在逐渐增大。

当梁弯曲时，在距中性层的距离为y处的纤维应变：

ε=My/(EI)

(1)

又有几何关系：

ε=yυ″

(2)

式中，υ″为中性轴的曲率。

将式(1)、(2)联立得：

M=EIυ″

由上式可得，动弯矩M和曲率υ″成正比，根据梁的振动理论，振型组成梁振动的完备空间，梁在荷载作用下的动弯矩是其振型的线性组合。对于不同跨径的四跨连续梁的1阶振型，各跨的最大曲率均在跨中，由于1阶振型在线性组合中占的比重最大，即该四跨梁的最大动弯矩也在跨中。因此对于跨中正弯矩效应的计算时，冲击系数采用基频是合理的。

当考虑中支座处的负弯矩效应时，随着支座2和支座4的对称外移，中支座处的曲率变大，内移则减小，但中支座处的曲率比其他2阶始终都大，并且中支座在2阶振型中首先出现反弯点，所以计算中支座处负弯矩效应时，冲击系数应采用2阶频率进行计算，而不能采用基频。

5 结 论

通过有限元计算和传统试验模态分析得出以下结论：

(1) 传统试验的模态分析结果和有限元的计算结果基本吻合，最大误差5.35%，最小误差不到1%。且越低阶，精度越高。因此模态分析理论对连续梁的振动的研究是基本可行的，且误差较低。

(2) 在计算桥梁的冲击系数时，不能一味选取基频作为计算的唯一变量。应按有限元分析或者传统检测去计算结构的频率和振型，参照结构正负弯矩与振型最大曲率选择恰当的频率。

(3) 对于不同跨径的对称四等跨连续梁桥，前3阶振型中，奇数阶振型关于中支座反对称；偶数阶振型关于中支座正对称。

(4) 随着对称支座的移动，第1、2阶振型随着跨径的减小，对应跨中的幅值和确率也减小；跨径增大，则对应跨中的幅值及曲率也增大。

(5) 对于四等跨连续梁，中支座在第2阶振型中率先出现反弯点；支座2和支座4则是在第3阶振型中率先出现反弯点；在不同跨径比下，随着支座2和支座4的内移，相应反弯点则出现在支座之外，外移则出现在支座之内。

(6) 在计算不同跨径的对称四等跨连续梁桥的跨中正弯矩效应时，依据《桥规》选取基频计算冲击系数时合理的。当计算支点负弯矩效应时，则应采用第2阶频率。

[1] JTG D60-2004.公路桥涵设计通用规范[S]．

[2] 王明明. 公路桥梁车桥动力相互作用的理论 分析及动载试验[J]. 黑龙江交通科技,2008(5):65-66.

[3] 许 鹏. 桥梁结构冲击系数影响因素研究与试验分析[D]．重庆：重庆交通大学，2013．

[4] 蒋培文. 公路大跨径连续体系桥梁车桥耦合振动研究[D]．西安：长安大学，2012．

[5] 蒋培文，贺拴海，宋一凡，等. 简支梁车桥耦合振动及其影响因素[J]．长安大学学报(自然科学版)，2013,33(1)：59-66．

[6] 漆景星.公路桥梁冲击系数计算方法研究[J]. 公路，2011(7) :85-88．

[7] 张为民. 大跨度混凝土公路桥梁冲击系数的探讨[J]．低温建筑技术，2009(5):42-43．

[8] 梁 君，赵登峰. 模态分析方法综述[J]．现代制造工程,2006(8)：139-141.

[9] 龙 英，滕召金，赵福水. 有限元模态分析现状与发展趋势[J].湖南农机,2009,36(4):27-28,45.

[10] 郭苏杰，王 俊，张宇峰. 运行模态分析技术在桥梁状态评估中的应用[J]．现代交通技术,2007,4(3)：42-44,48.

[11] 胡帮义,袁向荣,杨 勇,等. 4等跨连续梁模态试验分析及冲击因数研究[J]. 实验技术与管理,2015(8):70-74.

[12] 刘 辉，袁向荣，蔡卡宏,等. 五等跨连续梁模态分析试验及冲击系数[J]．实验室研究与探索，2016,35(5)：10-13.

[13] 袁向荣. 基于连续梁振动分析的桥梁冲击系数研究[J]．四川建筑科学研究,2013,39(4)：190-194.

[14] 李伟民,何 伟,杨 琳. 简支梁振动特性的理论 分析及实验研究[J]. 贵州教育学院学报, 2007(2):44-49.

[15] 徐文锋，袁向荣. DASP系统在连续梁模态分析中的应用[J]．工程与试验,2012,51(4)： 58-89,76.

Vibration Test Analysis of Four-unequal-span Continuous Beam and Discussion on Impact Coefficient

REN Zhangchen, YUAN Xiangrong, CHEN Zexian, DONG Xiangwan

(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

The natural frequency of the four-unequal-span continuous beam is analyzed and the changes of natural frequencies and vibration modes of the continuous beam are discussed with different span ratios. In test U-shaped beam is chosen. In addition to the natural vibration analysis and theoretical calculation of the model, finite element software is used to analyze and calculate the model with each span ratio. The results of finite element method are taken as references, and are compared with those obtained by traditional test, it proves the authenticity of the change law of mode. The results show that for the symmetric and four-unequal-span continuous beam, when the bearings are symmetrically moved, the first three modes of vibration are always symmetric or antisymmetric for the middle bearing, and the first bending point appears in the second vibration mode. For the mid span positive moment effect, the impact is calculated according to "bridge gauge"; for the negative moment effect of bearing, the impact factor should be calculated with second order frequency.

four-unequal-span continuous beam; modal analysis; vibration analysis; impact factor

2017-01-25

国家自然科学基金项目(51278137)

任张晨(1993-)，男，江苏南通人，硕士生，研究方向为桥梁检测工程、数字图像技术。

Tel.:15626029449； E-mail: 782818655@qq.com

袁向荣(1957-)，男，河北故城人，博士，教授，博士生导师，研究方向为桥梁工程分析计算检测、结构动力学分析与测试，数字图像处理。Tel.:13433926315； E-mail: rongxyuan@163.com

U 441.3

A

1006-7167(2017)08-0029-05