一种最大似然多普勒估计算法反解方法*
辛 颖,慕福奇,王 静,冷永清
(1.中国科学院大学 微电子学院,北京 100029; 2.江苏中科羿链通信技术有限公司,江苏 无锡 214135; 3.中国科学院微电子研究所,北京 100029)
一种最大似然多普勒估计算法反解方法*
辛 颖1,慕福奇2,王 静3,冷永清3
(1.中国科学院大学 微电子学院,北京 100029; 2.江苏中科羿链通信技术有限公司,江苏 无锡 214135; 3.中国科学院微电子研究所,北京 100029)
针对由最大似然多普勒估计算法目标函数反求出最大多普勒值计算量大的问题,提出了一种类二分搜索算法,该方法不用计算出所有可能的多普勒值的目标函数,就可以从多普勒估计目标函数反求出最大多普勒值。提出的算法从另一个角度减小了多普勒估计时的计算量。同时提出了根据估计出的多普勒瞬时值进行自适应平滑滤波,减小了最大似然多普勒估计算法的波动范围,提高了估计精度。
最大似然估计;多普勒;类二分搜索;自适应平滑
0 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)因其较高的频带利用率及传输数据率被广泛应用于IEEE 802.11、802.16、LTE等通信协议中[1]。在移动信道下,OFDM系统需要根据多普勒频移做很多适应性调整[1-3],如:信道追踪滤波器长度、切换算法参数等。现有的多普勒估计方法有利用不同OFDM符号之间频域的相关性的ML多普勒估计[1],其考虑了当多普勒扩展较大时,频域子载波之间较大的ICI影响。同时也有很多利用时域相关性计算多普勒的文章。参考文献[2]是直接利用OFDM符号之间的时域相关性,参考文献[4]是利用时域循环前缀(Cyclic Prefix, CP)与OFDM符号的后半段时域相关性。而文献[5-6]是利用导频符号的冲激响应之间的相关性求最大多普勒频移。
在由ML算法的目标函数反解出最大多普勒值时,文献[6]提出了一种穷举法,该方法是预设一个初值,计算出初值周围一定范围内目标函数值,此时得到一个使目标函数最小的值,再在这个最小值周围进行同样操作,逐渐迭代到待估计的多普勒值处。此方法需要频繁计算目标函数且需要多次迭代才能滑动到待估计的值。文献[7]采用查表的方式反求解最大多普勒值,该方法需要预先求出系统内的所有可能多普勒点的目标函数值,将其存在表格中,占用内存较大且查表时的搜索复杂度较大。文献[8]在多普勒频移较大时根据贝塞尔函数的曲线特征,用第一过零点检测法反解出最大多普勒值。该方法只适用于多普勒较大时且对噪声较为敏感。文献[9]中将目标函数中包含的第一类零阶贝塞尔函数近似成多项式,并通过求导的方式求得最大多普勒值,该方法只适用于多普勒较小的场景。针对从最大似然多普勒估计算法的目标函数反解出最大多普勒值的问题,本文提出了一种类二分搜索算法,该算法是直接求得多普勒值,但不像文献[6]那样将所有备选多普勒值的目标函数全部求出,只计算多普勒范围内的有限个点的目标函数值就能够反解出最大多普勒值,保留计算精度的同时减小了计算量。
1 系统模型及其最大似然多普勒估计
一个时分多址(Time Division Multiple Access, TDMA)OFDM系统的帧结构可以如图1所示。
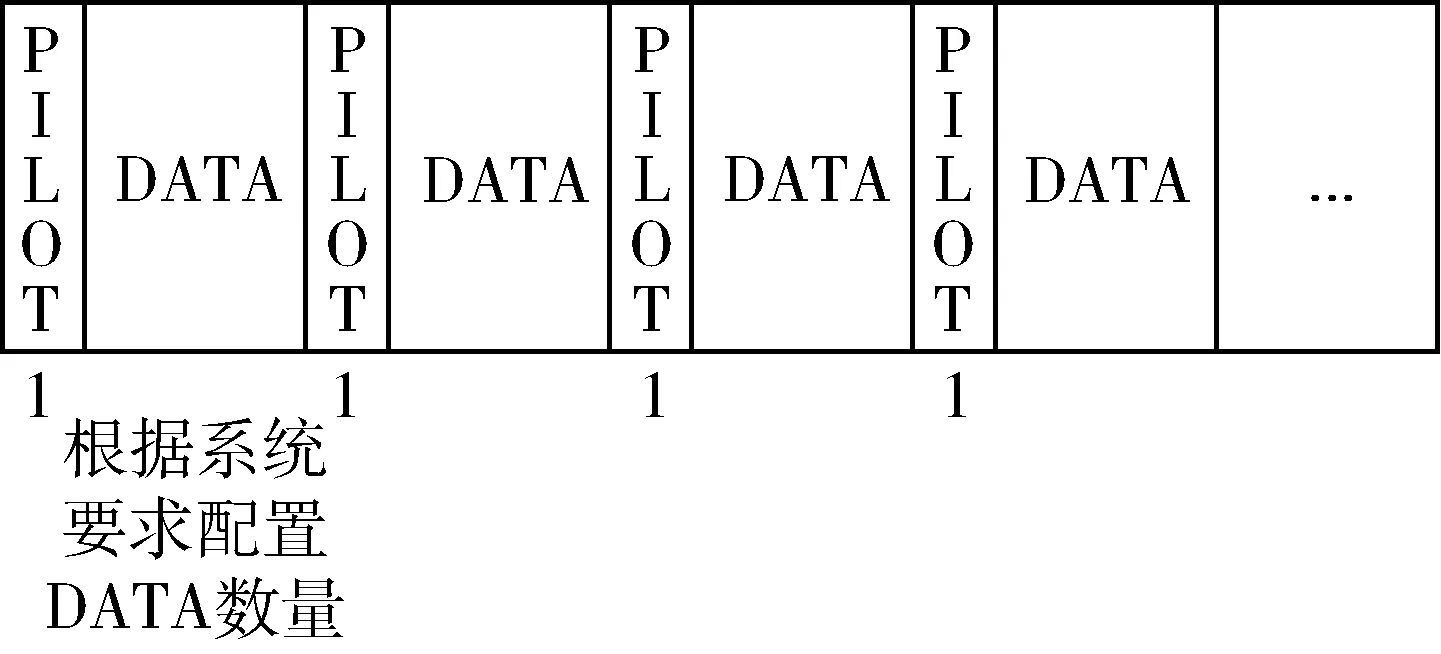
图1 TDMA-OFDM系统帧结构
假设该系统的一个OFDM符号有N个子载波,系统带宽是B,则时域的采样间隔为T=1/B,将一个已调制的信号X(k)进行傅里叶逆变换,得到OFDM已调信号:
(1)
在OFDM符号前端插入CP长度为Ncp,此时一个OFDM的符号长度Ts=(N+Ncp)T。将带CP的符号发送出去,经过多径Rayleigh衰落信道,其离散时域信道冲激响应表示为:
(2)
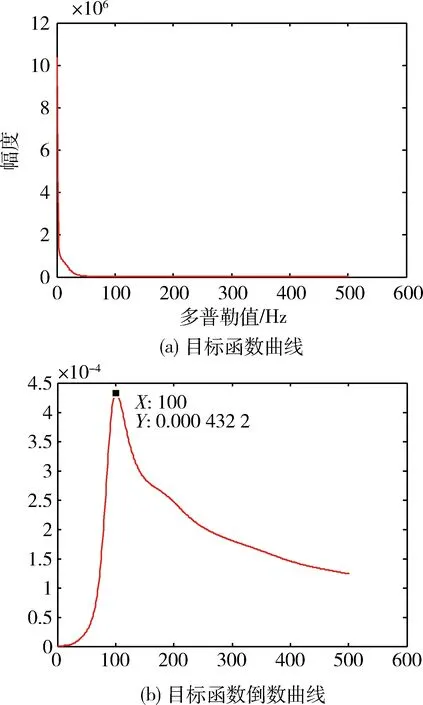
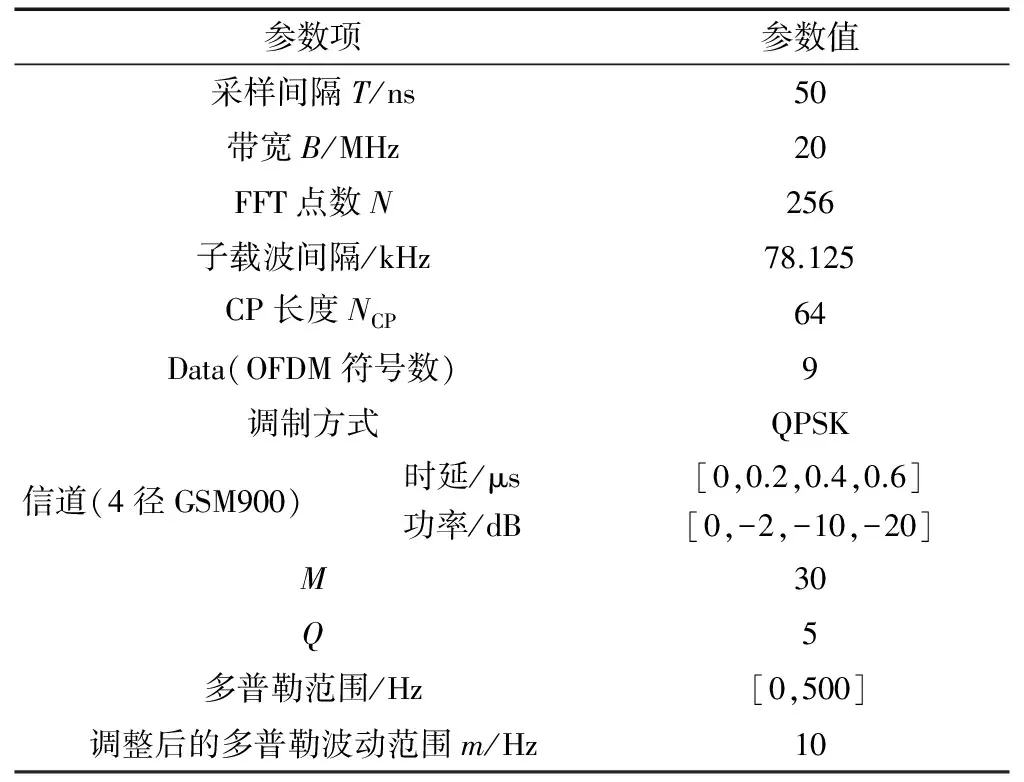
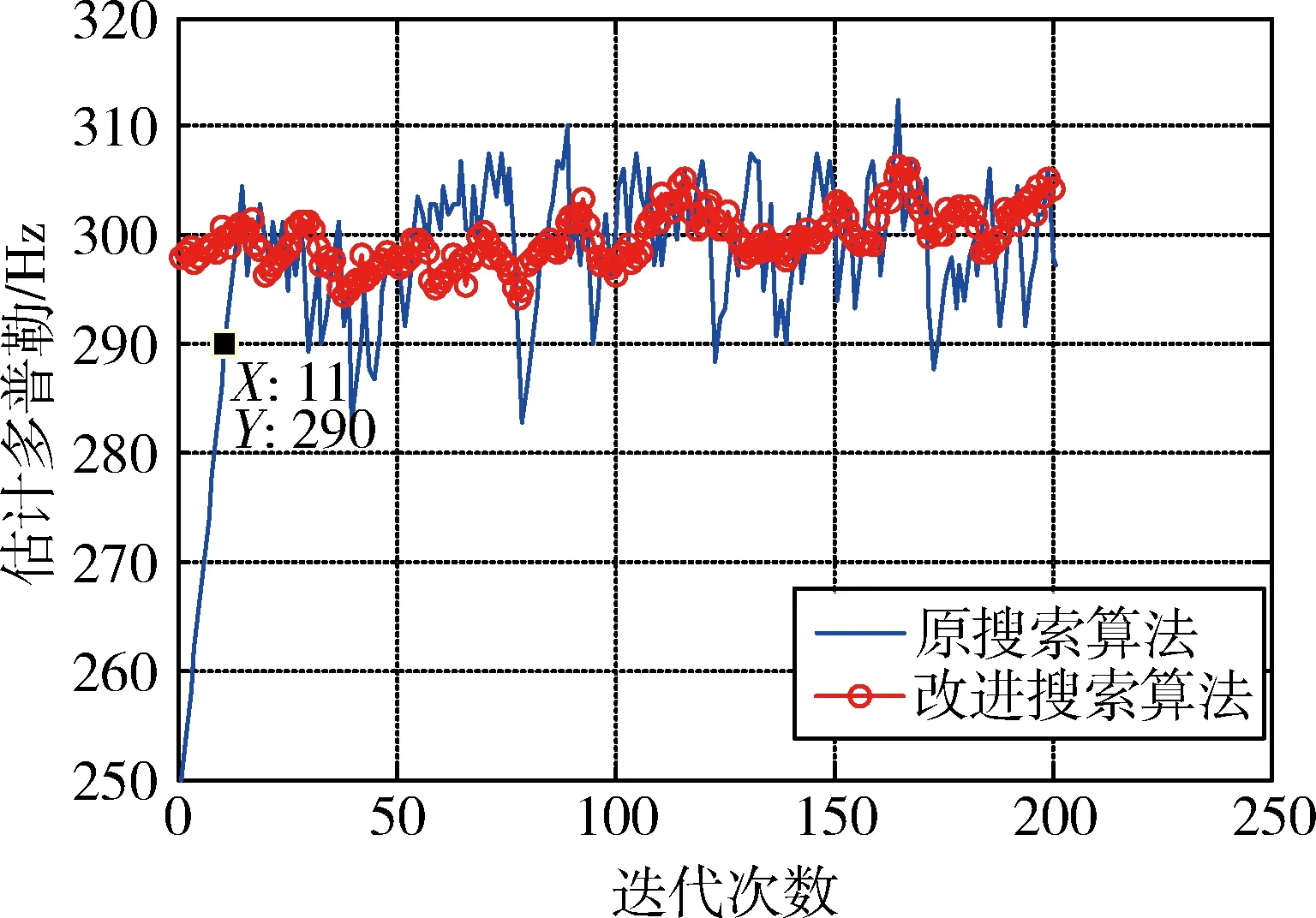
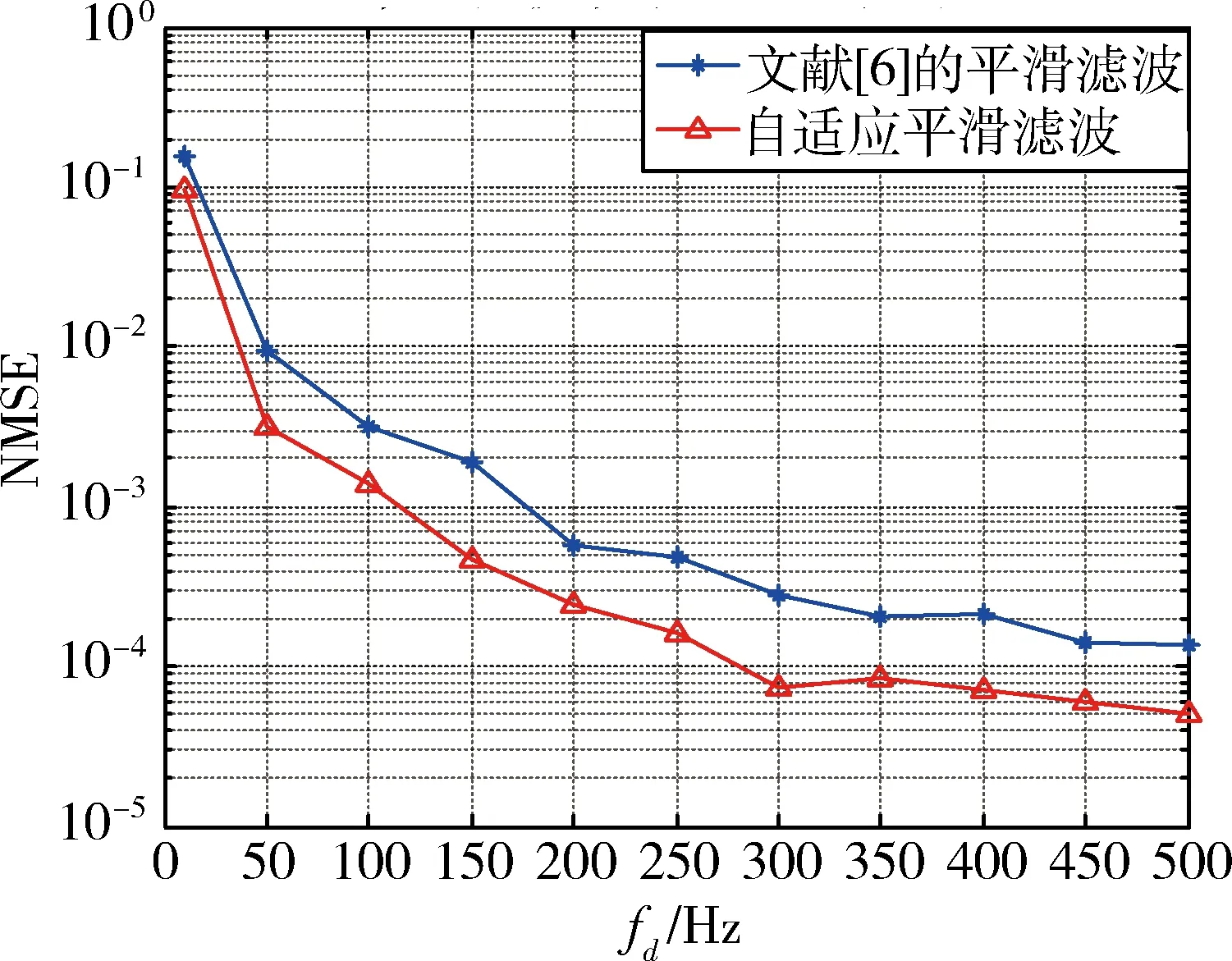
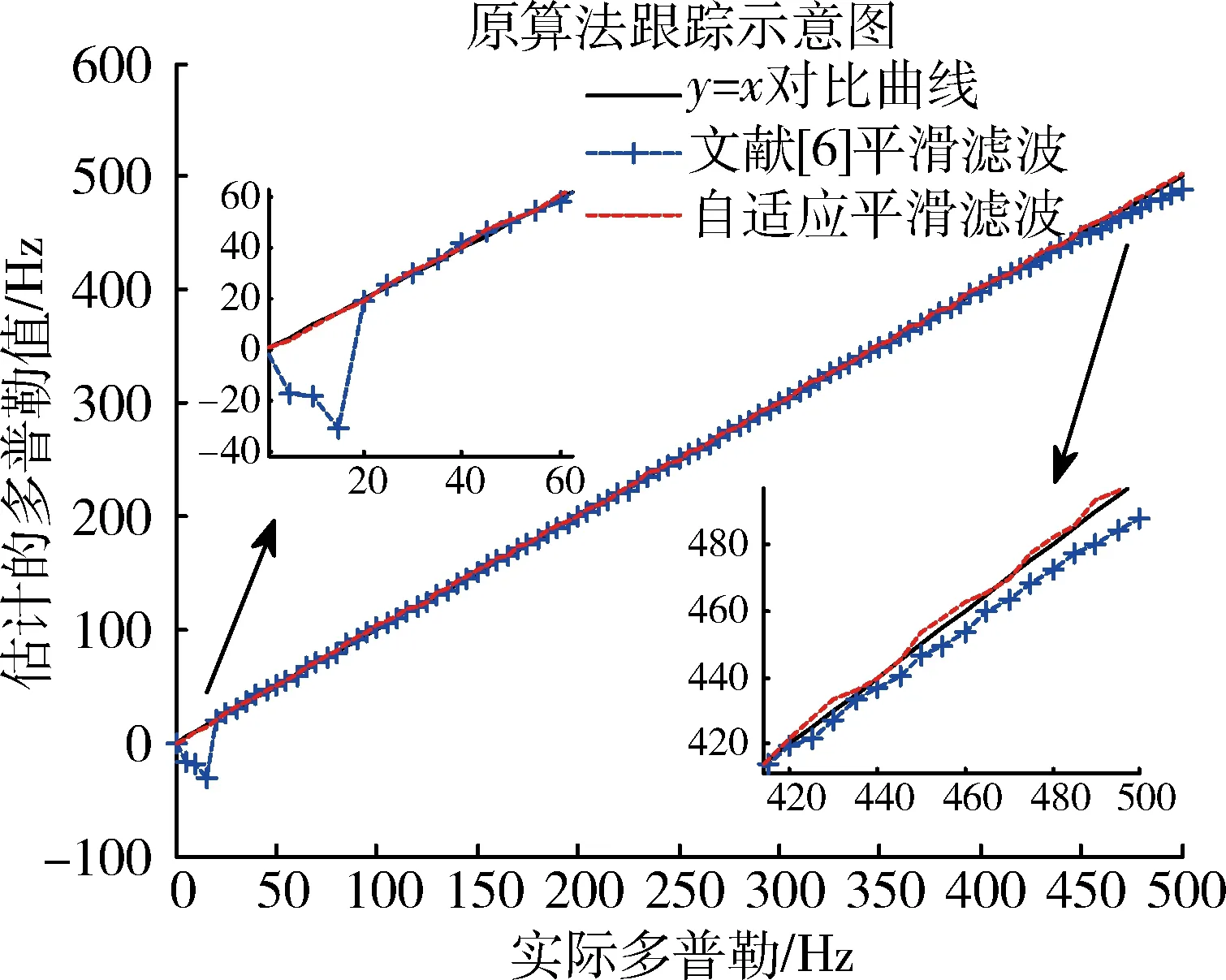
其中:L为多径信道长度,且L (3) 选取多径信道中的最强径用于追踪Rayleigh衰落信道下的信号变化,使其变成单径信道下多普勒估计问题。因本文的重点是研究如何从目标函数反解出最大多普勒值,所以这里直接给出ML算法的目标函数: (4) argmin表示使目标函数F(fd)取得最小值时的值,Γ表示fd的备选集,目标函数F(fd)在参考文献[6]由下式决定: (5) 此处将M个1pilot+data的形式看做一个slot,将第q个slot求得的时域信道冲激响应值组成hq,每Q个slot做一次平均。C(fd)为信道的相关矩阵[6]。简化的且标函数为: (6) 首先画出系统内所有可能多普勒值的目标函数及其倒数的曲线,如图2所示。图2(a)是在最大多普勒值fd=100 Hz时得到的系统内所有多普勒点的目标函数值。通过观察图2(b)可以推测出图2(a)的曲线特性:曲线在某点处取得最小值,在该点左侧单调递减,右侧单调递增。或者当最小值在曲线端点时,只有一个单调区间(递增或递减)。ML多普勒估计算法都是具有这样的特性,根据这种特性设计的反解算法可以适用于所有ML多普勒估计算法的反解问题。 图2 目标函数曲线图 二分搜索算法仅适用于单调函数,本文通过计算中间连续3点的值来判断缩小的范围,称之为类二分搜索算法,流程图如图3所示,具体步骤描述如下: 图3 类二分搜索算法流程图 2.1 搜索过程 (1)设定目标搜索范围[fdmin,fdmax] 此处可以根据该算法适用的系统确定多普勒可能的最大范围,一般fdmin=0 Hz,即表示静止时的通信,fdmax的取值可以根据所适用系统可能的最大移动速度,由多普勒频移的计算公式确定,计算公式为: (7) 上式中fdmax是最大多普勒频移,fc是系统的载波频率,v是相对移动速度(m/s),c是光速,为3×108m/s。 (2)判断fdmax-fdmin≥4与否 如果成立,说明待估计的多普勒范围内的点多于5个,就继续进入步骤(3);如果不成立,说明剩余的点小于等于4个,就直接计算出剩下点的目标函数值,在其中找出使目标函数值最小的点作为输出,即: (8) (4)比较F(n-1)、F(n)、F(n+1)的大小 如果F(n-1) 如果F(n-1)>F(n)>F(n+1),说明n-1、n、n+1三个点都处在左侧单调递减的曲线上,所以使F(fd)取得最小值的点在中间点n的右侧,缩小搜索范围为[n+1,fdmax],即fdmin=n+1,返回步骤(2)。 如果F(n-1)>F(n)&&F(n) 这样就得到了多普勒估计的一次瞬时值,但在长时间的多普勒估计中为减小单次估计的突发误差缩小估计的波动范围,本文通过设定门限,对估计的瞬时值进行自适应的平滑滤波。 2.2 自适应平滑滤波过程 (1)设定一个门限值th,该门限可以根据仿真确定。门限取得过大,起不到减小波动范围的目的;门限取得过小,当前一次估计值与真实值偏差较大时,滑动到真实值需要较长时间。 (9) 如果fd(n)超过了此波动范围,改变滤波系数: (10) 0<β<1是一个不依赖于多普勒估计的值,调换滤波系数的目的是:当本次瞬时估计值波动较大时,减小其在平滑滤波中的比重;波动不大时,则不改动滤波系数平滑滤波。 3.1 搜索算法仿真与分析 ML估计算法目标函数不尽相同,本文以式(5)为例,对提出的类二分搜索算法进行仿真,由于参考文献[6]的经典算法是需要已知SNR,所以SNR的变化对算法没多大影响,统一在SNR=17dB给出仿真结果,仿真参数如表1所示。 表1 仿真参数表 如图4所示,该图展示了在多普勒fd=300 Hz时的瞬时多普勒估计值输出,类二分搜索的目的是准确找出使目标函数取得最小值时的多普勒值,所以此处使用输出的瞬时值来展现类二分搜索过程可以在每次查找目标函数最小值时都非常精确。 图4 类二分搜索目标函数最小值与实际最小值的对比图 计算量的分析如表2所示。 表2 不同阶段计算量对比表 假设所适用系统的多普勒范围为0~500 Hz,所以备选多普勒集中有S=501个点。文献[6]需要计算约S=501次目标函数才能滑动到待估计的多普勒的波动范围内,而提出的类二分搜索算法只需要计算约3log2S=27次目标函数就能得到待估计的多普勒值,由此看出在收敛阶段中大大减小了计算量。同时结合图5可以看出,文献[6]需要从预设多普勒初值处经过约15次(时间约0.36 s)滑动才能到理想的波动范围,提出的类二分搜索算法只需要计算文献[6]中的1次(0.024 s)就可以收敛到理想波动范围,从而可以得出提出的类二分搜索算法在减小计算量的同时,缩短了收敛时间。同理可以讨论波动阶段的计算量,在本仿真中设调整后多普勒备选信号范围为前一次多普勒输出值的上下m点,此处取m=10 Hz。文献[6]的计算量是每计算2m=20次目标函数给出一次多普勒估计值,而提出的类二分搜索算法则每计算3log2(2m)=13次目标函数给出一次多普勒值。由此可以看出,本文提出的算法计算量在收敛阶段优势较为明显,在波动阶段相较于收敛阶段优势略次之。 图5 不同反解算法的收敛速度对比图 3.2 自适应平滑滤波仿真与分析 本文使用归一化均方误差(Normalized Mean Square Error,NMSE)来说明自适应平滑滤波计算出的多普勒值与真实值相比的波动情况,并与文献[6]的平滑滤波进行对比。NMSE定义[3]如下: (11) 如图6所示,自适应平滑滤波比文献[6]减小波动范围约3.68 dB。如图7所示自适应平滑滤波还可以改变文献[6]中在多普勒过低或过高时误差较大的问题。 图6 不同平滑滤波的NMSE对比图 图7 总体平滑滤波效果图 本文提出的用类二分搜索算法来优化ML多普勒估计算法,包括搜索过程与自适应平滑过程。搜索过程可以从ML多普勒估计算法的目标函数中反解出最大多普勒值,该方法不需要计算出所有多普勒点的目标函数值就可以得到结果,减小了计算量,加快了收敛速度。另外自适应平滑过程是根据每次得出的瞬时值自适应选择滤波系数,减小了随机误差的影响,从而使多普勒估计波动范围减小,增加了估计的精度。 [1] CHOI Y S, OZDURAL O C, Liu Huaping. A maximum likelihood doppler frequency estimator for OFDM systems[C]. IEEE International Conference on Communications,2006,10:4572-4576. [2] TSAI Y R, Yang Kaijie, TSAI C H. Low-complexity ML doppler spread estimation for OFDM systems [C]. IEEE Vehicular Technology Conference(VTC Fall),2011:1-5. [3] TEPEDELENLIOGLU C, ABDI A, GIANNAKIS G B. Estimation of doppler spread and signal strength in mobile communications with applications to handoff and adaptive transmission[J].Wireless Communications and Mobile Computing,2001,1(2):221-242. [4] SHOBER H, JONDRAL F. Velocity estimation for OFDM based communication systems [C]. IEEE Vehicular Technology Conference, 2002,2(2):715-718. [5] KRASNY L, ARSLAN H, KOILPILLAI D. Doppler spread estimation in mobile radio systems [J]. IEEE Communications Letters, 2001, 5(5): 197-199. [6] Cai Jueping, Song Wentao, Li Zan. Doppler spread estimation for mobile OFDM systems in rayleigh fading channels[J]. IEEE Transactions on Consumer Electronics,2003,49(4):973-977. [7] YUCEK T, TANNIOUS R M A. Doppler spread estimation for wireless OFDM systems [C]. IEEE/Sarnoff Symposium on Advances in Wired and Wireless Communication, 2005:233-236. [8] Hua Jingyu, You Xiaohu. Doppler shift estimation methods in mobile communication systems [J]. Journal of Southest University, 2004,20(4):405-411. [9] MAURTZ O. A hybrid method for doppler spread estimation[C]. Vehicular Technology Conference, 2004, 2: 962-965. A low-complexity ML Doppler spread estimation method Xin Ying1, Mu Fuqi2, Wang Jing3, Leng Yongqing3 (1. School of Microelectronics, University of Chinese Academy of Sciences, Beijing 100029, China; 2. Jiangsu Zhongke Yilian Communication Technology Co.,Ltd., Wuxi 214135, China; 3. Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China) A similar binary search algorithm is described forsolving the maximum-likelihood (ML)Doppler estimate equation. The proposed algorithm does not need to calculate all possible Doppler goal functions, but gives the outcome equally. It reduces the complexity of the ML Doppler approach in another way. Meanwhile, a self-adaptive smoothing filteris derived to smooth the instantaneous values and it gives a reduced fluctuation range with more accuracy. ML estimation; Doppler; similar binary search; self-adaptive smoothing filter 国家自然科学基金青年科学基金(61501455);北京市自然科学基金面上项目(4162068) TN929.5 A 10.19358/j.issn.1674- 7720.2017.15.022 辛颖,慕福奇,王静,等.一种最大似然多普勒估计算法反解方法[J].微型机与应用,2017,36(15):76-79,93. 2017-02-13) 辛颖(1989-),女,硕士研究生,主要研究方向:移动自组织网络的物理层设计。 慕福奇(1958-),男,学士,研究员,主要研究方向:移动自组织网络。 王静(1977-),女,博士,副研究员,主要研究方向:移动自组织网络。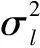
2 类二分搜索算法
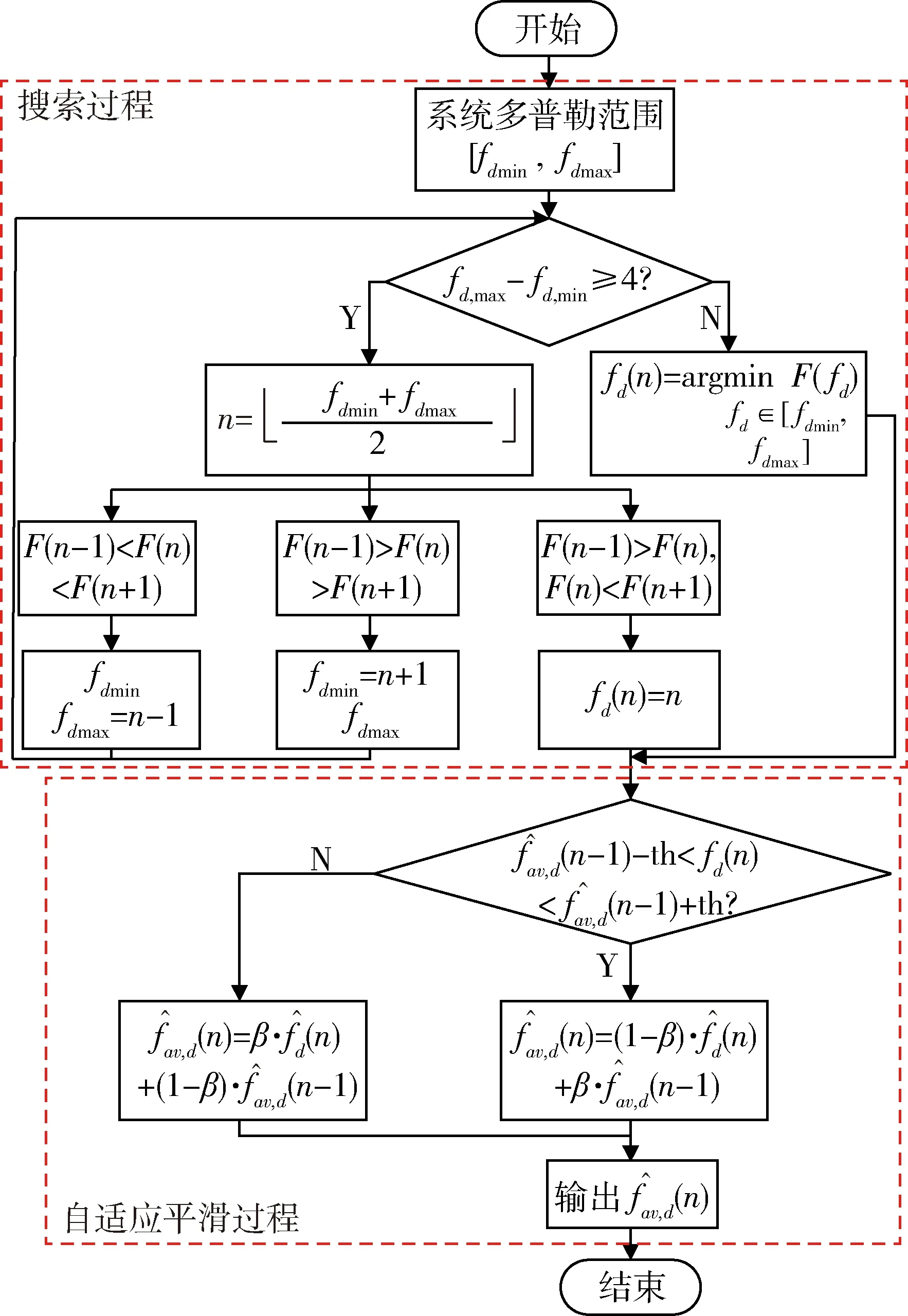


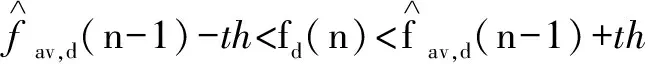


3 仿真与分析

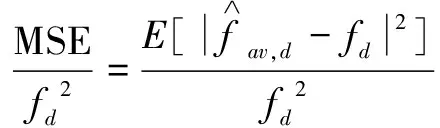
4 结论

