一种基于用户兴趣分析的协同过滤推荐算法

李 豪，张海英，张 俊

(1.中国科学院大学 微电子学院，北京 100029；2. 中国科学院微电子研究所 新一代通信射频芯片技术北京市重点实验室，北京 100029)

一种基于用户兴趣分析的协同过滤推荐算法

李 豪1,2，张海英2，张 俊2

(1.中国科学院大学 微电子学院，北京 100029；2. 中国科学院微电子研究所 新一代通信射频芯片技术北京市重点实验室，北京 100029)

传统的协同过滤推荐算法以用户对所有物品的评分向量作为计算用户相似度的依据，没有考虑到物品属性对用户兴趣的反映。为此，提出一种新的改进的相似度计算方法，引入了“用户兴趣分布矩阵”的定义，设计了启发式的评分预测方式，即根据兴趣相似度选出TOP-K用户之后，以用户标记的物品数量作为该用户的权重来预测评分。在Movielens数据集上的测试结果表明，改进后的算法相比传统的算法在平均绝对误差(MAE)上降低了7.3%。

协同过滤；兴趣分布；物品属性；用户权重

0 引言

目前协同过滤推荐算法领域已有了诸多研究，文献[1]介绍了协同过滤推荐技术的发展现状和存在的问题，从数据稀疏性、多内容推荐、可扩展性三方面总结了目前的协同过滤技术的研究进展。文献[2]通过粒子群优化算法确定K值的方式改进了传统的协同过滤推荐算法，降低了推荐的平均绝对误差。文献[3]通过多种用户属性分配权重的方法改进用户相似度的计算，结合Slope one算法填充评分矩阵，提高了推荐结果的准确率。文献[4]通过引入用户兴趣遗忘函数来改进Slope one算法。文献[5]提出了梯形模糊评分模型，挖掘离散评分中的用户观点，以此改进传统的协同过滤推荐算法。文献[6]从用户评论信息中提取用户观点，以此修正协同过滤推荐算法。文献[7]应用博弈论的方法对协同过滤系统中的用户评分行为进行分析，设计了一种均衡学习算法，对协同过滤推荐的机制具有启发价值。文献[8]通过矩阵分解的方式分析用户兴趣。文献[9]提出了结合Bhattacharyya系数的相似度计算方法，改善了数据稀疏情况下的推荐效果。文献[10]提出了基于K近邻图的快速协同过滤算法，在不牺牲准确率的情况下提高了计算速度。

上述这些研究着重于借助某种机制来修正传统的用户相似度计算方法，并没有关注到物品本身的属性对用户兴趣的反映。因此，本文提出了一种基于用户兴趣分析的相似度计算方法，结合物品的属性特点和用户的评分记录，引入了“用户兴趣分布矩阵”的定义，设计了启发式的评分预测方式，充分发挥了物品属性对用户兴趣的挖掘，推荐结果在平均绝对误差方面相比传统的协同过滤推荐有了显著提高。

1 相关工作

1.1 相似度计算方法

目前常见的相似度计算方法有余弦相似度、修正的余弦相似性、Pearson相关系数。

假设系统中总共有N个用户以及M个物品，用U={u1,u2,…,uN}表示用户集合，I={i1,i2,…,iM}表示物品集合，用户ui对所有物品的评分记为：

Ri=[Ri,1Ri,2Ri,3…Ri,M]

用户对物品的评分记为矩阵R：

R=[R1R2R3…RM]T

其中Ri,j表示用户ui对物品ij的评分。

(1)余弦相似度

将每个用户对所有物品评分信息看成M维向量，用户ui和用户uj的余弦相似度定义为：

(2)修正的余弦相似度

余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，因此无法衡量每个维度上数值的差异，修正的余弦相似度通过给每个维度的数值减去用户对物品的平均评分，改善了这个缺点。假设用户ui和uj共同评分的物品集合为Ii,j，用户ui的评分物品集合为Ii，用户uj的评分物品集合为Ij，用户ui和uj的修正余弦相似度定义为：

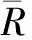
(3)Pearson相关系数

用户ui和uj的Pearson相关系数定义为：

已有实验结果表明，利用Pearson相关系数计算相似度得到的推荐效果比其他两种方法更好[11]，因此在后面的实验中，将使用基于Pearson相关系数的协同过滤推荐算法作为参照，来对比本文所提出的基于用户兴趣的相似度计算方法。

1.2 评分预测方法

通过相似度的计算，为用户u找到相似度最高的前K个用户，记为集合S，用集合S中的这K个用户对物品的评分信息来预测用户u的评分情况，用Pu,i表示用户u对物品i的预测评分，传统的评分预测公式如下：

2 改进算法描述

从上述介绍可以看出，传统的推荐算法主要依靠用户对物品的评分习惯来判断用户之间的相似性，而没有考虑物品本身的属性对用户兴趣的反映。在实际应用中，很多推荐系统中的物品都具有明显的类别属性，不需要通过聚类就有了一些属性标签，比如电影物品的“科幻”、“爱情”、“动作”，音乐物品的“流行”、“古典”、“乡村”。这些属性是物品本身所具有的，在很大程度上影响了用户的评分情况，反映出用户兴趣的分布，因此，引入“用户兴趣分布”的概念作为衡量用户之间相似度的标准是非常有意义的。

2.1 用户兴趣分布矩阵

假设推荐系统中物品的固有属性有T个，Ai表示物品ii的属性向量，则Ai={a1,a2,a3,…aT}，其中aj的取值为0或1，0表示物品没有此属性，1表示物品具有此属性，一个物品可以具有多种属性，所有物品的属性矩阵记为A，则：A=[A1A2A3… AM]T

用户ui在这些属性上的兴趣分布向量记为：

Fi=[Fi,1Fi,2Fi,3…Fi,T]

那么，所有用户的“兴趣分布矩阵”记为：

F=[F1F2F3…FM]T

用户在某个属性上的兴趣，可以通过两方面体现出来，一是标记了具有这个属性物品的多少，二是对具有此属性的物品的打分高低。以电影物品为例，比如某用户标记了300部电影，其中200部“科幻”电影、20部“爱情”电影，给这200部科幻电影的平均打分是3.5，给这20部爱情电影的平均打分是4.5。直观地看，该用户对科幻电影的兴趣更大，因为经常观看科幻电影，但是从打分情况来看，爱情片更容易让该用户满意。一种很常见的原因是，用户选择观看的爱情片是那些公认的优秀电影，所以即使观看数量很少，但是自己的满意度很高。一个个性化推荐系统，除了推荐用户明显感兴趣的物品，还要挖掘用户潜在的兴趣，因此对于这种情况，“科幻”和“爱情”都应该作为该用户推荐的重点考虑因素，也就是说数量和评分都是用户兴趣的重要反映。

将用户评分矩阵R中的非零值全部变成1，便得到用户标记物品矩阵C。用户标记的物品在T个属性上的数量分布矩阵记为X，则：

X=C×A

(1)

用户标记的物品在T个属性上的平均评价记为矩阵Y，则：

(2)

矩阵没有除法，上式的分母分子均为N×T的矩阵，此处所定义的“除法”为分子分母矩阵中对应位置的元素相除。

为了方便不同用户之间进行比较，需要对X和Y中每一行的向量进行归一化处理，归一化的方式为：

(3)

归一化后的矩阵记为X′和Y′，矩阵X′表明了用户兴趣在T个属性上的数量分布，矩阵Y′反映了用户兴趣在T个属性上的评价分布，那么用户的“兴趣分布矩阵”定义为：

F=X′×β+Y′×(1-β)

(4)

上式中的参数β取值在0到1之间，这个参数是为了权衡数量和评价对用户兴趣的反映，在后面的实验中，会对β进行多种取值，通过比较推荐效果选取最好的β值。

2.2 改进的评分预测方式

(5)

其中，αv表示用户v所标记的物品数量。

2.3 改进的协同过滤算法模型

为了提高推荐效果，在实际应用中，需要先对用户或者物品进行聚类，然后在类中对用户进行TOP-K相似用户的筛选。结合上述用户兴趣分布的定义和改进的评分预测方式，改进的协同过滤推荐算法步骤如下：

(1)基于用户评分矩阵，使用 K-means算法对用户进行聚类，类别个数为P；

(2)按照式(1)～式(4)计算出用户兴趣分布矩阵；

(3)按照用户兴趣分布向量，使用余弦相似度计算用户之间的兴趣相似度；

(4)对于用户u，在所在簇中筛选出TOP-K相似用户，然后按照式(5)进行评分预测；

(5)对所有用户执行步骤(4)，得出评分预测。

采用篇名词检索法在中国知网（CNKI）数据库进行关键词检索。检索篇名词：群众体育；时间范围：2008年1月1日～2017年12月31日；检索时间：2018年5月24日21:39。由于学位论文存在发表期刊的情况，为保证研究的严谨性，本研究剔除检索到的学位论文，共检索到群众体育相关文献共计963篇，将963篇文献分别以“Refworks”格式及“End-note”格式导出。采用Citespace V软件对这些文献进行可视化分析，将文献中的数据以图表的形式反馈出来，从而更加直观、立体地对我国群众体育研究的时空分布特点、热点及历史演化进行分析。

3 实验及结果分析

在本节中，先使用K-means算法对用户进行聚类，然后将传统协同过滤推荐算法和基于用户兴趣分析的协同过滤推荐算法进行比较，并对实验结果进行对比分析。

3.1 实验设计

3.1.1 评价指标

评分预测的准确性一般使用平均绝对误差MAE (Mean Absolute Error)作为指标，MAE的定义为：

其中Pu,i表示用户u对项目i的预测打分，Qu,i表示用户u对项目i的真实打分，MAE越小表示预测结果越准确。

3.1.2 数据集

实验采用的是明尼苏达大学的GroupLens 小组建立的非盈利的电影推荐系统MovieLens中的用户数据，选取规模为100 K的数据集进行试验。此数据集中有943个用户对1 682部电影的评分数据，评分值是1～5的离散值，所有评分项共有十万条，因此数据集的稀疏度为1-100 000/(943×1 682)=94%。数据集中的物品为“电影”，共有19个属性。数据集的80%作为训练集，20%作为测试集，共有5组这样的“base-test”数据集，可以用来重复5次实验。

3.1.3 参数设计

在2.3节介绍的改进的协同过滤推荐算法中，影响实验结果的参数有3个，一是用户聚类的个数P，二是选择TOP-K相似用户的K值，三是式(4)中的β值。在实验中，用户聚类个数P分别取值2、3、4、5、6；K分别取值10、15、20、25、30、35、40、45、50；β取值从0.1、0.2、0.3、…、0.9。

3.2 实验结果

对于改进的协同过滤算法，在β=0.5的情况下，P分别取值2、3、4、5、6，计算对测试集预测评分的MAE，结果如图1所示。可以看出在P=2的情况下，无论K如何取值，评分预测的MAE总是最小的，在K=20时MAE最小，因此将用户聚为两类、选取TOP20的相似用户进行推荐是准确性最好的方案。

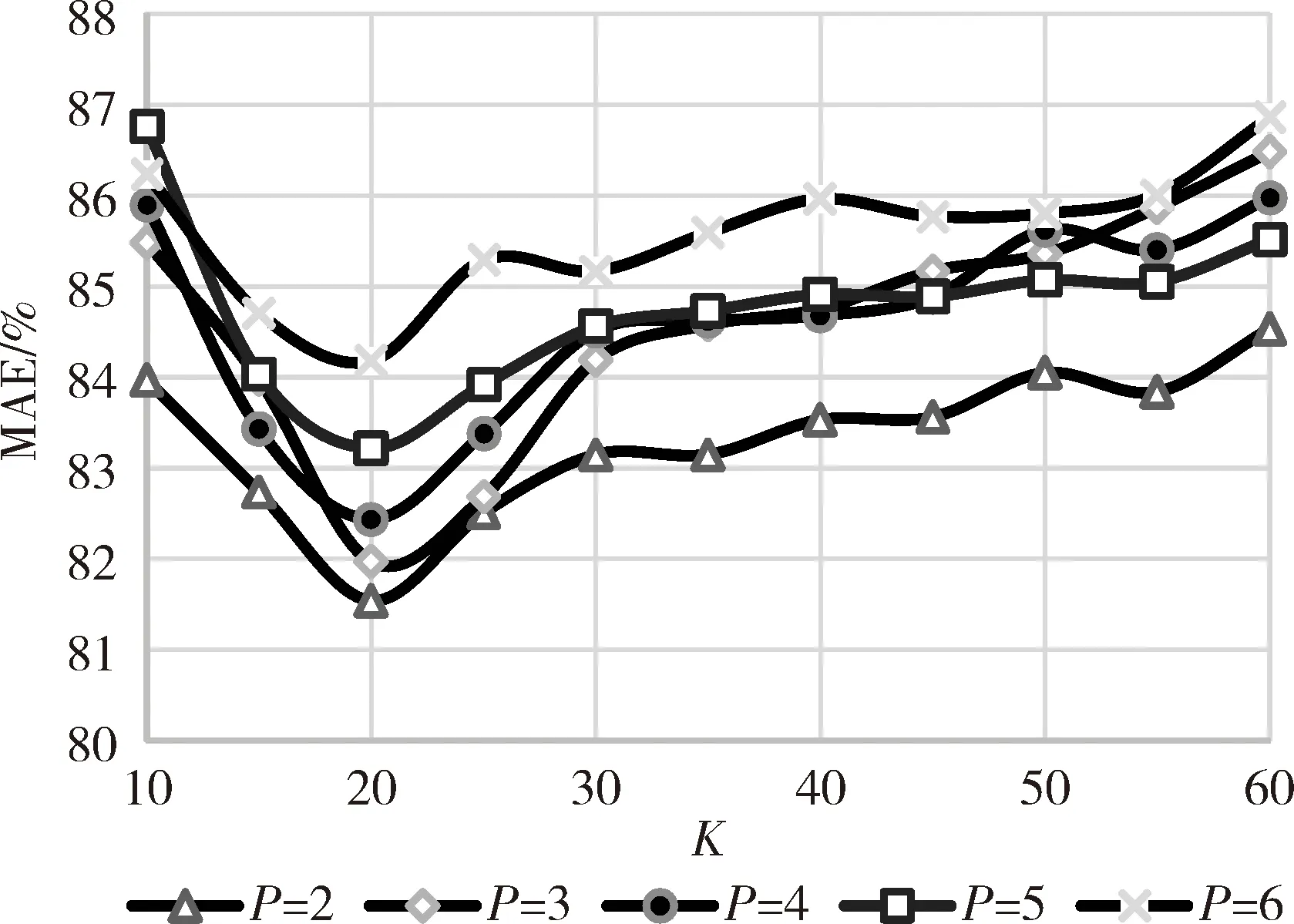
图1 改进算法在β=0.5时，不同P值下的MAE

对于改进的算法，在P=2、K=20的情况下，β取值从0.1、0.2、0.3到0.9，实验结果如图2所示。可以看出当β=0.5时，改进的算法效果最好，此时的MAE为81.54%。

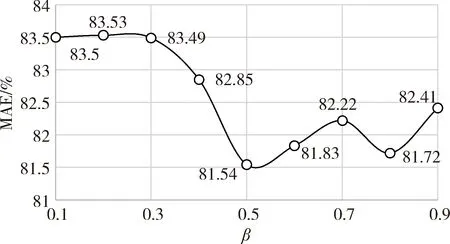
图2 改进算法在不同β值下的MAE

对于传统的协同过滤推荐算法，取P=2，K=10、15、20、25、30、35、40、45、50，实验结果如图3所示，可以看出在K=20时，该算法得到最优的MAE，为87.94%。

对比图2和图3可以发现，改进的协同过滤推荐算法，MAE从原来的87.94%降低到81.54%，降低了7.3%，因此，可以得出结论：改进的协同过滤推荐算法在一定程度上提高了评分预测的准确性。

图3 传统CF推荐算法在不同K值下的MAE

4 结束语

本文通过在传统的协同过滤推荐算法中引入用户兴趣分析，在不增加算法时间复杂度的情况下，使得评分预测的平均绝对误差降低了7.3%，推荐结果的准确性得到提高。但仍然存在一些不足，比如算法的空间复杂度增加了，在用户数量和物品种类特别大的系统中，需要占用大量内存来计算预测结果；而且没有考虑到用户兴趣随着时间变化的迁移，可以考虑在用户兴趣分布的计算中引入物品的时间函数来修正，不过这样会增加算法时间复杂度，对于响应速度要求比较高的系统来说不太适合。

[1] 冷亚军，陆青，梁昌勇．协同过滤推荐技术综述[J]．模式识别与人工智能，2014，27(8)：720-734.

[2] 硕良勋，柴变芳，张新东．基于改进最近邻的协同过滤推荐算法[J]．计算机工程与应用，2015，51(5)：137-141.

[3] 赵文涛，王春春，成亚飞，等.基于用户多属性与兴趣的协同过滤算法[J].计算机应用研究，2016，33(12)：3630-3633,3653.

[4] 李桃迎，李墨，李鹏辉．基于加权Slope one的协同过滤个性化推荐算法[J]．计算机应用研究，2017，33(8)：1-6.

[5] 吴毅涛，张兴明，王兴茂，等.基于用户模糊相似度的协同过滤算法[J]．通信学报，2016，37(1)：198-206.

[6] 李伟霖，王成良，文俊浩.基于评论与评分的协同过滤算法[J].计算机应用研究，2017，34(2)：1-7．

[7] 徐蕾，杨成，姜春晓，等.协同过滤推荐系统中的用户博弈[J].计算机学报，2016，39(6)：1176-1189.

[8] HERNANDO A, BOBADILLA J, ORTEGA F. A non negative matrix factorization for collaborative filtering recommender systems based on a Bayesian probabilistic model[J]. Knowledge-Based Systems, 2016, 97(c): 188-202.

[9] PATRA B K, LAUNONEN R, OLLIKAINEN V, et al. A new similarity measure using Bhattacharyya coefficient for collaborative filtering in sparse data[J]. Knowledge-Based Systems, 2015, 82(c): 163-177.

[10] PARK Y, PARK S, JUNG W, et al. Reversed CF: A fast collaborative filtering algorithm using a k-nearest neighbor graph[J]. Expert Systems with Applications, 2015, 42(8): 4022-4028.

[11] CASTRO-SCHEZ J J, MIGUEL R, VALLEJO D, et al. A highly adaptive recommender system based on fuzzy logic for B2C e-commerce portals[J]. Expert Systems with Applications, 2011, 38(3): 2441-2454.

A collaborative filtering recommendation algorithm based on user interest analysis

Li Hao1,2, Zhang Haiying2, Zhang Jun2

(1.School of Microelectronics, University of Chinese Academy of Sciences, Beijing 100029, China; 2. Beijing Key Laboratory of Radio Frequency IC Technology for Next Generation Communications, Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China)

The original collaborative filtering recommendation algorithm uses the user′s score vector for all items as the basis for calculating the user′s similarity, which does not take into account the reflection of the object′s interest to the user′s interest. In this paper, an improved similarity calculation method is proposed. The new algorithm introduces the definition of “user interest distribution matrix”, and designs the heuristic scoring method. The TOP-K users are selected according to the similarity degree of interest, then the number of marked items is used as the weight of the user to predict the score. The results of the test on the Movielens dataset show that the improved algorithm is 7.3% lower than the traditional algorithm in the Mean Absolute Error (MAE).

collaborative filtering; interest distribution; item properties; user weight

TP39

A

10.19358/j.issn.1674- 7720.2017.15.007

李豪，张海英，张俊.一种基于用户兴趣分析的协同过滤推荐算法[J].微型机与应用，2017,36(15)：25-28.

2017-03-13)

李豪(1993-)，男，硕士研究生，主要研究方向：机器学习和数据挖掘。

张海英(1964-)，女，研究员、博士研究生导师， 主要研究方向：健康电子，物联网技术，医疗大数据平台。

张俊(1983-)男，硕士，助理研究员，主要研究方向：健康电子，物联网技术，数字信号处理。