有关切点弦问题的说题感悟与拓展

广东省佛山市第一中学(528000) 吴统胜

有关切点弦问题的说题感悟与拓展

广东省佛山市第一中学(528000) 吴统胜

本文从一次有关切点弦问题的说题展开,不断将已知条件、结论等进行变式拓展,并结合由变式拓展得到的高考题,较详细地归纳总结了有关切点弦问题的高考基本题型、解决这类问题的基本策略及有关切线方程、切点弦问题的一般化的结论.

说题题目 设P为直线l:x−y−2=0上的点,过点P作抛物线C:x2=4y的两条切线PA、PB,其中A、B 为切点.当点P(x0,y0)为直线l上的定点时,求直线AB的方程.

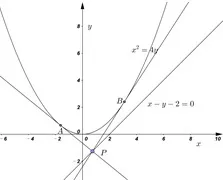
图1

一.学生情况分析

我校是广东省重点中学,学生素质相对较高,但解析几何中求轨迹问题虽在新课中有所涉及,但题型、方法方面学生掌握还不够熟练、系统!

二.题目分析

这是一道以抛物线为载体利用参数法求轨迹方程的问题,主要考查了曲线与方程、直线和抛物线等基础知识、求轨迹方程的基本方法、方程化简的基本技能和综合运用数学知识解决问题的能力,该题同时还涉及了函数与方程、转化与化归、数形结合等数学思想方法,是一道很不错的题目!直线与圆锥曲线的位置关系一直是高考命题的热点,解析几何的基本思想就是利用代数的方法研究几何问题.

因此在解题过程中计算占较大的比重,对运算求解能力的要求较高,其解法主要涉及函数方程、数形结合的思想.求轨迹方程问题是解析几何中的一类重要题型,有时与导数结合考查直线与曲线的位置关系,具有典型性和代表性.解析几何的解答题往往是中高档题,常常涉及的内容是求轨迹方程、直线和圆锥曲线的位置关系、对称、最值、范围等.在知识交汇处命题是解析几何命题的显著特征,常与平面向量、三角函数、不等式、数列、导数、立体几何等知识结合,考查综合分析问题、解决问题的能力及运算求解能力.

求轨迹常用方法有直译法、定义法、代入法、参数法、交轨法等,2010年广东理20(1)考查的是交轨法求轨迹方程,2011年广东考查的是定义法求轨迹方程.该题原型为2013年广东理科20题第(II)问:

题目 已知抛物线C的顶点为原点,其焦点F(0,c)

(I)求抛物线C的方程;

(II)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;

(III)当点P在直线l上移动时,求|AF|·|BF|的最小值.

三.解题分析

设直线l:x−y−2=0上的定点P(x0,y0),过点P作抛物线C:x2=4y的两条切线PA、PB,其中A、B为切点.求两切点所在直线AB的方程.

求轨迹常用方法有直译法,定义法,代入法,参数法,交轨法等,但根据该题已知条件不可能是直译法、定义法、交轨法、代入法(即相关点法),故可考虑参数法,若采用参数法,关键是如何引入参数,若以切线斜率为参数,设P(x0,y0),y0=x0−2,再由点斜式设出设先分别设出切线PA、PB方程:y−(x0−2)=k1(x−x0),y−(x0−2)=k2(x−x0),还要利用相切条件,联立抛物线C:x2=4y利用判别式等于零去解,求出A、B坐标再利用两点式求直线方程,思路虽清晰简单,但显然过程太繁琐,且运算量大,不易消元,不妥!

换个思路,设切点坐标A(x1,y1),B(x2,y2),(x1/=x2),以x,x为参数,利用导数几何意义,可12表示出切线PA、PB方程,再利用P(x0,y0)在两切线上,将y0=x0−2代入切线方程看看,边做边观察,边调整,设切线AP的方程为:

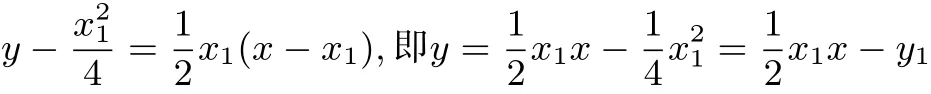
切线BP的方程为:

再将P(x0,y0)代入得:y2.如何消去参数x1,y1,x2,y2?细心观察发现A(x1,y1),B(x2,y2),(x1/=x2)其实都满足方程:即都在同一条直线上,故直线AB的方程为:即x0x−2y−2y0=0.

点评 本题解题关键在于恰当引入坐标参数x1,x2,进而表示出两条切线方程,将给出的相切的几何条件(切线斜率)恰当地转化为代数条件(切点处的导数值),再利用P(x0,y0)在两切线上得y0=x0−2,设而不求,整体消元得直线AB方程,大大简化了运算量.要引导学生对数学思想方法进行归纳提炼,优化解题思维,简化解题过程.

一般规律总结:求在点P(x0,y0)处的切线方程只需将曲线方程中的x,y,x2,y2分别以,xx0,yy0代换即可得所求切线方程;若过曲线外一点P(x0,y0)分别作曲线的两条切线PA,PB,A,B为切点,类似地,只需将曲线方程中的x,y,x2,y2分别以xx0,yy0代换即可得切点弦AB所在的直线方程.掌握这个一般规律,可以快速准确地解决有关切点弦的问题.

四.变式拓展

1.将 P(x0,y0)由定·点·变为直线 AB 上的动·点·,在运动变化过程中考查学生分析解决问题的能力,同时考查定点问题.

拓展1 求证:直线AB恒过定点,并求出该定点坐标.

解析 将y0=x0−2代入直线AB的方程:x0x−2y−2y0=0,整理得x0(x−2)−2(y−2)=0.令

即直线AB恒过定点(2,2).

2.将已知条件中的抛物线改为椭圆

拓展2 设P为直线l:x−y−2=0上的点,过点P作椭圆C:+y2=1的两条切线PA、PB,其中A、B为切点.当点P(x0,y0)为直线l上的定点时,求直线AB的方程并求证直线AB恒过定点.

解析 利用上述总结的一般规律将椭圆方程中的x2,y2分别以x0x,y0y代换即可得切点弦AB所在的直线方程+y0y=1,即xx0+3yy0−3=0.再将y0=x0−2代入AB方程得:x0x+3(x0−2)y−3=0,即x0(x+3y)−3(2y+1)=0,令

3.将已知条件中的抛物线改为圆,考查直线与圆、切线长、最值问题

拓展3 设P为直线l:x−y−2=0上的点,过点P作圆C:x2+y2=1的两条切线PA、PB,其中A、B为切点,设坐标原点为O.

(1)当点P为直线l上的定点时,求直线AB的方程;

(2)当点P为直线l上的动点时,

①求证:直线AB恒过定点,并求出该定点坐标;

②求切线长PA、PB的最小值;

③求四边形PAOB面积的最小值;

④求△AOB面积的最大值.

4.增加圆x2+y2=1的已知条件

拓展4 抛物线y=x2的动弦AB所在直线与圆x2+y2=1相切,分别过点A、B的抛物线的两条切线相交于点M,求点M的轨迹方程.

又x1+x2=k,x1x2=−b,过点A的抛物线的切线方程为:y−x21=2x1(x−x1),即

同理过点B的抛物线的切线方程为:

点评 增加圆x2+y2=1的已知条件后,在考查抛物线简单性质的同时又考查了直线与圆相切、直线与抛物线相交和轨迹问题,综合性强,运算求解难度大,还考查了思维的严密性,是一道相当好的改编题!

5.增加条件:AB是过抛物线x2=2py(p＞0)焦点F动弦

拓展5已知AB是过抛物线x2=2py(p＞0)焦点F的动弦,O是坐标原点,过A,B两点分别作此抛物线的切线,若两切线相交于点P.

(1)求点P的轨迹方程;

图2

(2)求证:PA⊥PB.

将拓展5中的条件结论互换又可得:

拓展6 已知P是抛物线x2=2py(p＞0)准线上的动点,O是坐标原点,过点P分别作此抛物线的切线PA,PB,A,B为两切点

(1)求点AB过抛物线焦点F;(2)求证:.PA⊥PB.

拓展7 考查轨迹问题及平面几何证明问题

(2005年江西理科22)如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x−y−2=0上运动,过P作抛物线C的两条切线PA,PB,且与抛物线C分别相切于A,B两切点.

图3

(1)求△APB的重心G的轨迹方程;

(2)证明:∠PFA= ∠PFB.

图4

(1)求椭圆C的标准方程;

(2)若点P(x0,y0)为圆x2+y2=a2+b2上的动点,点P到椭圆C的两条切线分别为PA,AB,A,B为切点,求证:PA⊥PB.

若将拓展8中第(2)问条件结论互换可得拓展9,即为2014广东高考第20题:

拓展9(2)若动点P(x0,y0)为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程.

拓展10 考查定值、面积问题

拓展11 考查定点、定值、范围问题

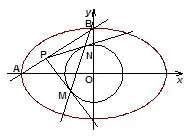
图5

(3)若存在点P使得△PMN为正三角形,试求椭圆离心率e的取值范围.

图6

连接ON,OM,OP,若存在点P使△PMN为正三角形,则在Rt△OPN 中,OP=2ON=2r=c,所以(关键之处!数形结合!)a2b2≤c2(a2+b2),a2(a2−c2)≤c2(2a2−c2),得e4−3e2+1≤0.因为0＜e＜1,所以

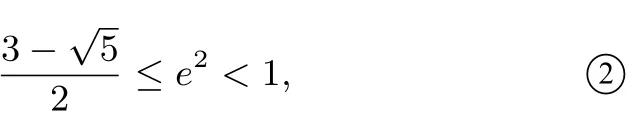
点评 该题可以较好地考查直线、圆、椭圆基础知识和定值、范围等问题,考查了考生运算求解能力和转化与化归、数形结合等数学思想方法,可以较好地检测考生的数学能力和数学素养.

五.感悟反思

从国际视野的角度看,当今的数学教育趋势就是以理解为价值取向!以问题解决为价值取向!以数学探究为价值取向!因此,科学、合理、现代的数学高考就是要考数学理解!考数学问题解决!考数学探究!教师要抓好课堂教学,在重视基础知识和基本技能教学的同时,注重提升学生对数学思想方法和数学本质的理解水平.教师要精选习题,多设计能考查数学主体内容、体现数学素质的题目,反映数、形运动变化的题目,研究型、探索型或开放型的题目,让考生独立思考,自主探索,发挥主观能动性,研究问题的本质,寻求合适的解题工具,梳理解题程序,为考生展现创新意识、发挥创造能力创设广阔的空间!选题要注重基础性、典型性、综合性、启发性、开放性和探究性,且要注重一般性的解题规律和方法(即通性通法);要精选一些一题多变、一题多解、多题归一、有层次、有拓展的题目开阔学生思路,使学生能有新的体会和收获;要重视课本中的典型例题、习题和最近几年的高考题、高考模拟题,多些对课本例题、习题和高考题的进行改编与拓展.课堂教学中教师要引导学生重视对函数与方程、转化与化归、数形结合、分类讨论等数学思想方法的感悟及解题规律的总结与提升,提高学生的数学解题能力与数学素养.

题海无涯,感悟是岸!数学好学、好用、好玩,要引导学生学好、用好、玩好数学!