基于三维梁理论的电磁轨道炮复合身管抗弯性能分析

尹冬梅， 肖宏成， 栗保明

(南京理工大学 瞬态物理国家重点实验室， 江苏 南京 210094)

基于三维梁理论的电磁轨道炮复合身管抗弯性能分析

尹冬梅， 肖宏成， 栗保明

(南京理工大学 瞬态物理国家重点实验室， 江苏 南京 210094)

基于复合材料的三维厚壁梁理论，考虑梁的三维应变、挠曲等效应，建立了圆形电磁轨道炮身管纤维缠绕复合外壳的等效抗弯刚度计算模型。采用组合梁的等效抗弯刚度计算法，对纤维缠绕的轨道炮身管的整体抗弯刚度进行了分析，并与层合板理论法、有限元法做了对比。结果显示，3种计算方法在缠绕角度较大时，计算结果一致性较好。分析了纤维缠绕角度的变化、不同径向位置的碳纤维缠绕角度变化以及不同内膛绝缘材料对身管轴向抗弯刚度的影响。研究结果表明：身管的轴向抗弯刚度在缠绕角度较小时，随着缠绕角度的增大，呈明显的下降趋势，并且其受内层碳纤维的缠绕角度影响要比外层碳纤维的要大；高密度、高弹性模量的内膛绝缘材料并不一定就能提高身管的轴向抗弯刚度。

兵器科学与技术； 三维梁理论； 电磁轨道炮； 身管； 层合板理论； 抗弯刚度

0 引言

复合材料在电磁轨道炮身管中应用比例的增加，可以减轻身管质量，从而更好地满足电磁轨道炮身管轻量化设计的要求，但这将意味着对身管刚度的设计提出了更高要求。根据文献[1-2]中的研究，对于大口径轨道炮身管，特别是悬臂结构的轨道炮身管，在轴向需要表现出较大的柔性，例如：由于身管的自重，身管将发生弯曲下垂，高速发射时身管的横向振动等，都将使弹枢离开炮口时的速度方向偏差较大，影响命中精度。研究表明，提高身管的抗弯刚度，可以改善这一问题。但至今为止，对于由多种材料复合的轨道炮身管的抗弯性能分析，见诸报道的很少。对此，本文对纤维缠绕的轨道炮身管的抗弯刚度进行研究。

本文将纤维缠绕轨道炮身管视为一个由两部分组成的组合梁结构，即身管纤维缠绕外壳以及由内部绝缘支撑材料和导轨组成的内部复合结构。对于身管纤维缠绕外壳，本文将其视为复合材料层合管构件。目前,复合材料层合管构件抗弯刚度的理论计算方法[3-4]主要有：经典层合板理论、基于纯弯构件应力应变场计算的弹性理论和梁理论。这些理论被广泛地应用于不同的工程实际问题中，例如，文献[5]基于层合板理论，对含金属内衬的纤维复合材料发射筒的三维等效弹性模量进行了计算，进而对其抗弯刚度进行了分析。但此方法，忽略了壳体的曲率影响，将三维应力应变关系退化为平面状态。Xia等[6]基于纯弯构件应力应变场计算的弹性理论，通过定义Lekhnitskii应力函数，对纤维缠绕增强的复合材料夹层管的抗弯性能进行了分析。文献[7]基于薄壁梁理论对4种不同铺层的薄壁圆形管件的抗弯刚度进行了计算，并与试验结果做了对比，效果较好。Kim等[8]基于厚壁梁的高阶剪切理论，假定扭转是均匀的，对复合材料圆管的抗弯刚度进行了预测，但计算比较复杂。由于电磁轨道炮身管纤维缠绕外壳相对普通复合材料层合管构件较厚，故本文将基于复合材料厚壁梁理论，考虑三维应变、主次挠曲等效应，采用较为简便的方法建立身管纤维缠绕外壳的抗弯刚度计算模型，然后采用组合梁的抗弯刚度计算方法对纤维缠绕的轨道炮身管的整体等效抗弯刚度进行分析。

1 电磁轨道炮身管纤维缠绕外壳的抗弯刚度计算模型

1.1 运动学分析

由于纤维缠绕角度的不同将引起身管纤维缠绕外壳在轴向抗变形能力的差异，并且轨道炮身管纤维缠绕层往往比较厚，故可将其看作一个厚壁梁来进行分析，假设：

1)纤维缠绕外壳的材料是均质且连续的各向异性材料；

2)纤维缠绕外壳的横截面轮廓在其平面内不变形，即保持其原形不变；

3)同时考虑纤维缠绕外壳的主、次挠曲效应；

4)考虑横向剪切效应，剪切应变γzs、γzn在纤维缠绕外壳的横截面内均匀分布；

5)纤维缠绕外壳发生的变形均为线弹性变形；

6)采用圣维南非均匀扭转模型。

为了描述纤维缠绕外壳的几何结构，定义了全局笛卡尔坐标系(x,y,z)和局部曲线坐标系(s,z,n)，如图1所示。其中曲线坐标的坐标原点位于中面线上，n为中面线的法线方向，s为中面线的切线方向，α定义了相对于s的纤维缠绕方向角，与传统意义的缠绕角β(即缠绕纤维纵向与芯模(或管件)轴向的夹角)之和为90°. 笛卡尔坐标系的原点位于纤维缠绕外壳的横截面的几何中心，根据上述假设，基于梁理论，外壳截面上任意一点在笛卡尔坐标系中的三维位移场[4,9-10]为

u(x,y,z)=u0(z)-yφ(z)，

(1)

v(x,y,z)=v0(z)+xφ(z)，

(2)

w(x,y,z)=w0(z)+θx(z)y+θy(z)x-
φ′(z)[Fw(s)+nrs(s)]，

(3)

式中：u、v和w分别为沿x轴、y轴和z轴方向的位移；u0(z)、v0(z)和w0(z)分别代表沿x轴、y轴和z轴的刚体平移位移；θx(z)、θy(z) 和φ(z)分别为沿x轴、y轴和z轴的转动位移；Fw为挠曲函数；rs为中面线上任一点在曲线坐标系中沿s方向的坐标。

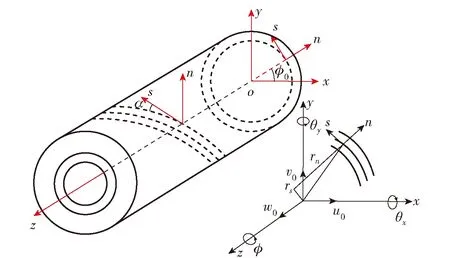
图1 电磁轨道炮身管纤维缠绕外壳的坐标系关系Fig.1 Relationship between coordinate systems for filament- wound housing of railgun barrel

该点在笛卡尔坐标系中的坐标可以用中面线上的点坐标表示为

(4)

(5)

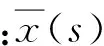
挠曲函数可表示为

(6)

式中：Ψ为扭转函数；rs(s)、rn(s)分别为中面线上任一点在曲线坐标系中分别沿s方向、n方向的坐标，并可以表示为

(7)

(8)

1.2 应变- 位移关系

基于上述假设，可以得到以下应变场：

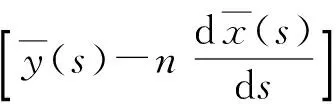
(9)

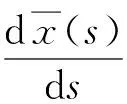
(10)

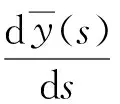
(11)

式中：εzz、γsz和γnz分别为轴向应变、环向剪切应变和横向剪切应变；δ为中面线围成的面积与其周长的比值。

假设，n轴与x轴的夹角为φ0，则

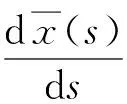
(12)

1.3 本构方程

对于正交各向异性的纤维缠绕外壳，其任意第k层的非材料主方向坐标系(曲线坐标系)下，应力应变关系为

(13)

式中：Qij为偏轴刚度矩阵，可由正轴刚度矩阵通过坐标转换计算而得。

根据文献[4，8]，在无内外压力场作用时，缠绕层横截面面外应力相对于面内应力是小量，可以忽略，故假设：

σss=σnn=σsn=0.

(14)

但由于泊松比效应，横截面面外应变不能忽略，则

εss=co1εzz+co2γsz,

(15)

εnn=co3εzz+co4γsz,

(16)

γns=co5γzn,

(17)

式中：co1、co3分别为z方向引起的s方向和n方向的泊松耦合系数；co2、co4分别为s方向和n方向的剪拉耦合系数；co5为交叉耦合系数。其表达式如下：

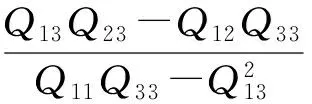
由(13)式～(17)式可将应力表示为

(18)

式中：C11=Q12co1+Q22+Q23co3；C12=Q12co2+Q23·co4+Q36；C21=Q16co1+Q26+Q36co3；C22=Q16co2+Q36co4+Q66；C33=Q44+Q45co5.

1.4 内力平衡方程的建立和等效抗弯刚度的计算

作用在纤维缠绕外壳截面上的合力和合力矩，可通过将缠绕层上的应力沿外壳截面积分得到：

Tz(z)=∬AσzzdndS,

(19)

My(z)=∬AσzzxdndS,

(20)

Mx(z)=∬AσzzydndS,

(21)

(22)

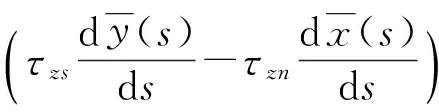
(23)

Mz(z)=∬AσzzwdndS,

(24)

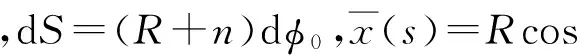
将(18)式代入(19)式～(24)式，并忽略位移的高阶微分项可得到内力和位移的关系为

(25)

式中：aij与纤维绕外壳的各向异性及其截面的几何结构有关。

对于圆形复合材料管件，常见的缠绕方式为层合管环向刚度一致型(CUS型)缠绕方式。根据文献[4,6,8-9]的研究，对于CUS型，可将(25)式做进一步的简化，并假设纤维缠绕外壳只受沿x轴的弯曲载荷作用，根据(25)式可求得该弯矩与曲率之间的关系为

(26)

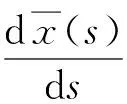
根据材料力学中弯矩、抗弯刚度以及曲率之间的关系，可得该纤维缠绕外壳的等效抗弯刚度为

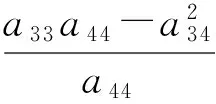
(27)

2 电磁轨道炮身管整体的轴向抗弯刚度计算模型

本文将轨道炮身管看作一个复合材料组合梁结构，则可根据组合梁的等效轴向抗弯刚度[1,7,11]计算方法，得到轨道炮身管整体的轴向抗弯刚度为

(28)

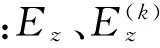
若以如图2所示的圆口径轨道炮身管结构为例，根据上述计算方法，该身管的轴向抗弯刚度可由内部轨道(结构1和结构2)、内膛绝缘材料(结构3和结构4)的轴向抗弯刚度和身管纤维缠绕外壳(结构5)的轴向抗弯刚度叠加而成，即

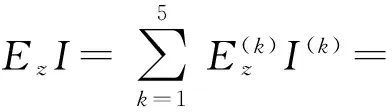
(29)

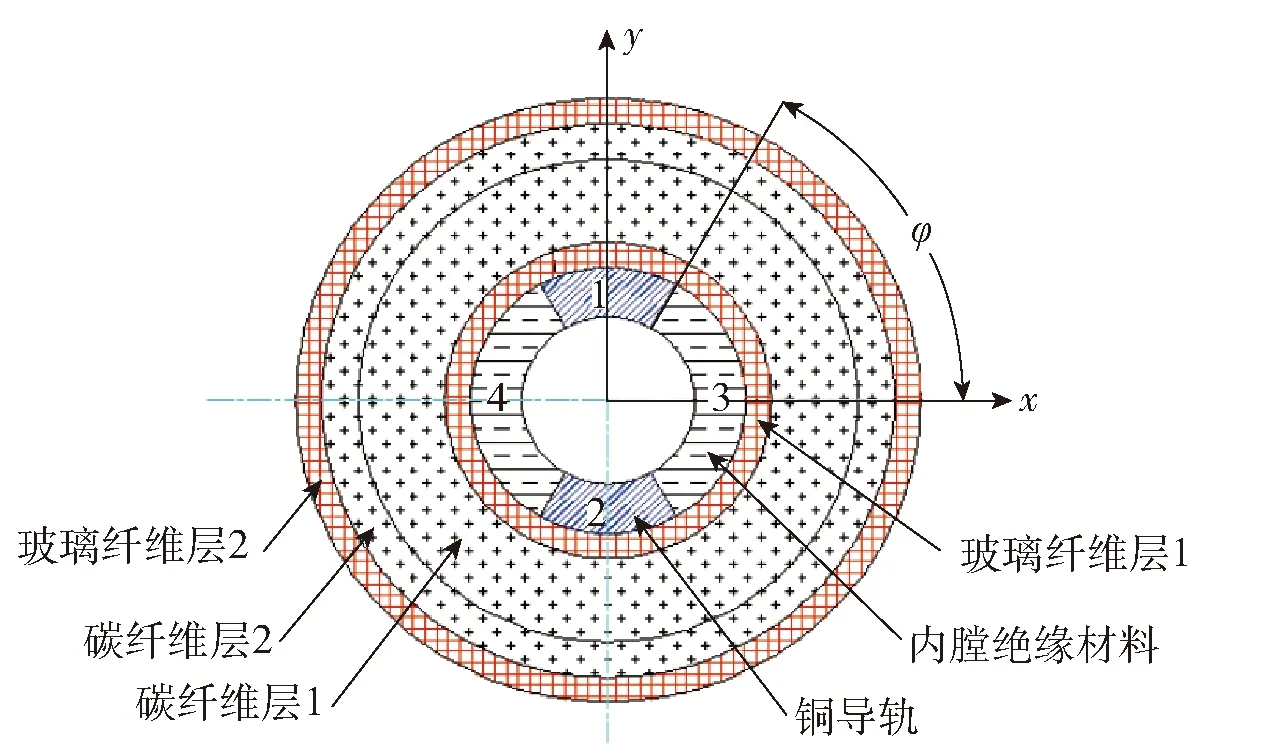
图2 电磁轨道炮纤维缠绕身管的结构示意图Fig.2 Structure of filament wound barrel for railgun

本文所采用的算例中，身管的内膛半径为25 mm，身管悬臂端长为4 m，其相关几何结构参数如表1所示，材料参数如表2和表3所示。内膛轨道与内膛绝缘材料均视为各向同性材料。该轨道炮身管的复合外壳由碳纤维和玻璃纤维以±α角度混合缠绕而成，其轴向抗弯刚度可以由上述方法计算得出。

表1 纤维缠绕材料的设计参数

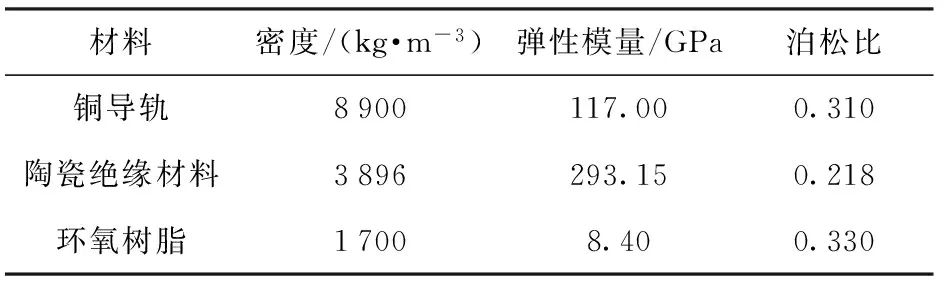
表2 铜导轨和内膛绝缘材料的材料参数

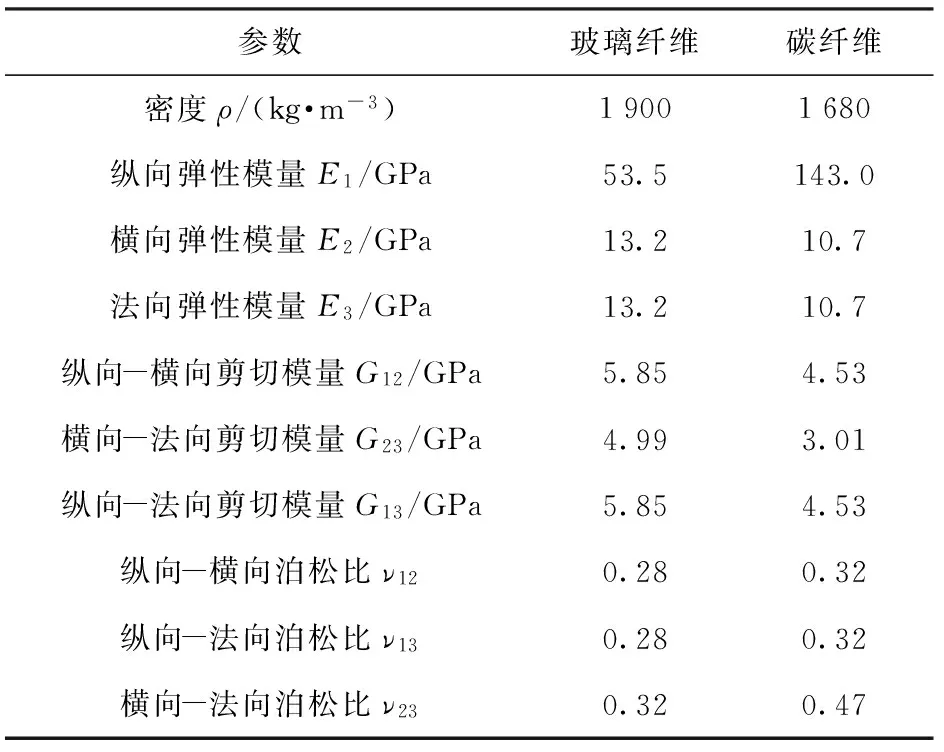
表3 纤维缠绕外壳的材料参数

假设如图2所示的内膛轨道与内膛绝缘材料的邻界面和y轴的夹角φ=60°，对于不同的纤维方向角α=900-β时，由(27)式、(29)式可计算出该结构的轨道炮身管的整体轴向抗弯刚度值。

3 计算与分析

图3显示了用3种方法计算的不同缠绕角度β下，该结构的轨道炮身管(内膛绝缘材料为陶瓷)的整体轴向抗弯刚度值的变化曲线。其中方法1三维梁理论(本文所采用的方法)，方法2层合板理论(基于层合板理论计算纤维缠绕外壳的等效轴向弹性模量的方法)，方法3有限元法(通过轴向加载计算身管整体等效轴向弹性模量的方法)。通过比较，3种方法计算结果均显示：随着缠绕角度的增大，身管的轴向抗弯刚度在缠绕角度较小时，呈明显的下降趋势；在缠绕角度较大时，变化幅度较小，并出现稍微上升。这是因为缠绕角度越小，纤维纵向弹性模量对身管的轴向模量贡献越大，故而身管的轴向抗弯刚度就越大，但此时纤维对身管径向的变形约束作用减弱，从而削弱了身管径向的刚度。根据文献[5]的研究，纤维缠绕圆管的强度性能主要由环向纤维层决定，这是因为纤维材料具有很强的各向异性，尤其是力学性能，纵向性能要优于横向性能，当某一方向性能增强，与此方向垂直的方向性能就将减弱，故而当采用较小的纤维缠绕角度时，管件的强度性能就受到削弱。

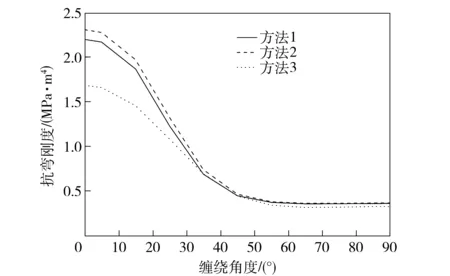
图3 电磁轨道炮身管的轴向抗弯刚度值随缠绕角度的变化值Fig.3 Change of axial bending stiffness of railgun barrel with winding angle

3种计算方法在缠绕角度较大时，计算值一致性较好。在缠绕角度较小时，方法1和方法2的计算结果相对差距较小，但与方法3的计算结果相差较大，其中方法1的结果相对更接近方法3。这是因为与方法2相比，方法1考虑了身管纤维缠绕外壳的三维应变效应，但都还未能综合考虑身管内膛绝缘材料和导轨在内的身管整体的三维应力应变效应。

根据前期研究表明，缠绕角度较小时，碳纤维缠绕比玻璃纤维缠绕对身管的轴向抗弯刚度的贡献要大，为此，本文对碳纤维缠绕做了进一步的研究，即分别变化碳纤维缠绕层1和缠绕层2的缠绕角度，其他纤维缠绕层的缠绕角度均保持45°不变，计算了身管的轴向抗弯刚度值，如图4所示。通过对比可知，当缠绕角度较大时，身管的抗弯刚度受碳纤维层1和纤维层2的β角度变化影响较小。当缠绕角度小于45°时，碳纤维层1的缠绕角度减小时，身管抗弯刚度值增加的幅度比碳纤维层2的缠绕角度减小时身管抗弯刚度值增加的幅度要大。可见，同等条件下，减小内部碳纤维层的缠绕角度可更有效地增加身管的抗弯刚度值。

图4 电磁轨道炮身管轴向抗弯刚度随碳纤维层缠绕角的变化Fig.4 Change of axial bending stiffness of railgun barrel with winding angle of carbon fiber layer

轨道炮的结构设计中，内膛的陶瓷绝缘材料有时会采用环氧树脂绝缘材料，这势必将对身管的抗弯刚度产生影响。为此，以上述结构为例，将陶瓷材料换成环氧树脂材料，计算了身管抗弯刚度的变化，如图5所示。为了表述方便，内膛绝缘材料分别为陶瓷和环氧树脂时的身管称为陶瓷身管和环氧树脂身管。随着缠绕角度的增加，陶瓷身管和环氧树脂身管的轴向抗弯刚度也基本随之减小，由于陶瓷的弹性模量比环氧树脂的高，故而相同的缠绕角度下，身管的抗弯刚度也较大。

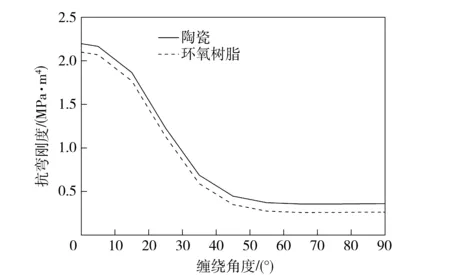
图5 含不同内膛绝缘材料的身管轴向抗弯刚度随缠绕角度的变化Fig.5 Change of axial bending stiffness of railgun barrel with different bore insulators with winding angle

为了进一步研究绝缘材料对抗弯刚度的影响，根据材料力学中悬臂梁的挠度计算方法[1]，计算了这两种身管自重作用下的悬臂自由端的位移，如图6所示。通过对比发现，随着缠绕角度的增大，两种身管悬臂自由端的位移变化趋势是一致的，均随着缠绕角度的增大而增大，这与其本身的轴向抗弯刚度的变化趋势是相反的。但是，在缠绕角度较大时，陶瓷身管的悬臂自由端的位移明显较小，而在缠绕角度较小时，两种身管悬臂自由端位移相近，甚至环氧树脂身管的悬臂自由端的位移略小。这是因为身管悬臂自由端位移和身管自重与身管抗弯刚度的比值呈正比，尽管在相同的缠绕角度时，陶瓷身管的轴向抗弯刚度比环氧树脂身管的大，但陶瓷材料的密度较大，导致其自重较大，而在较小的缠绕角度时，陶瓷身管的轴向抗弯刚度随缠绕角的减小而增加的幅度没有环氧树脂身管的大，导致二者比值比环氧树脂身管的略大。

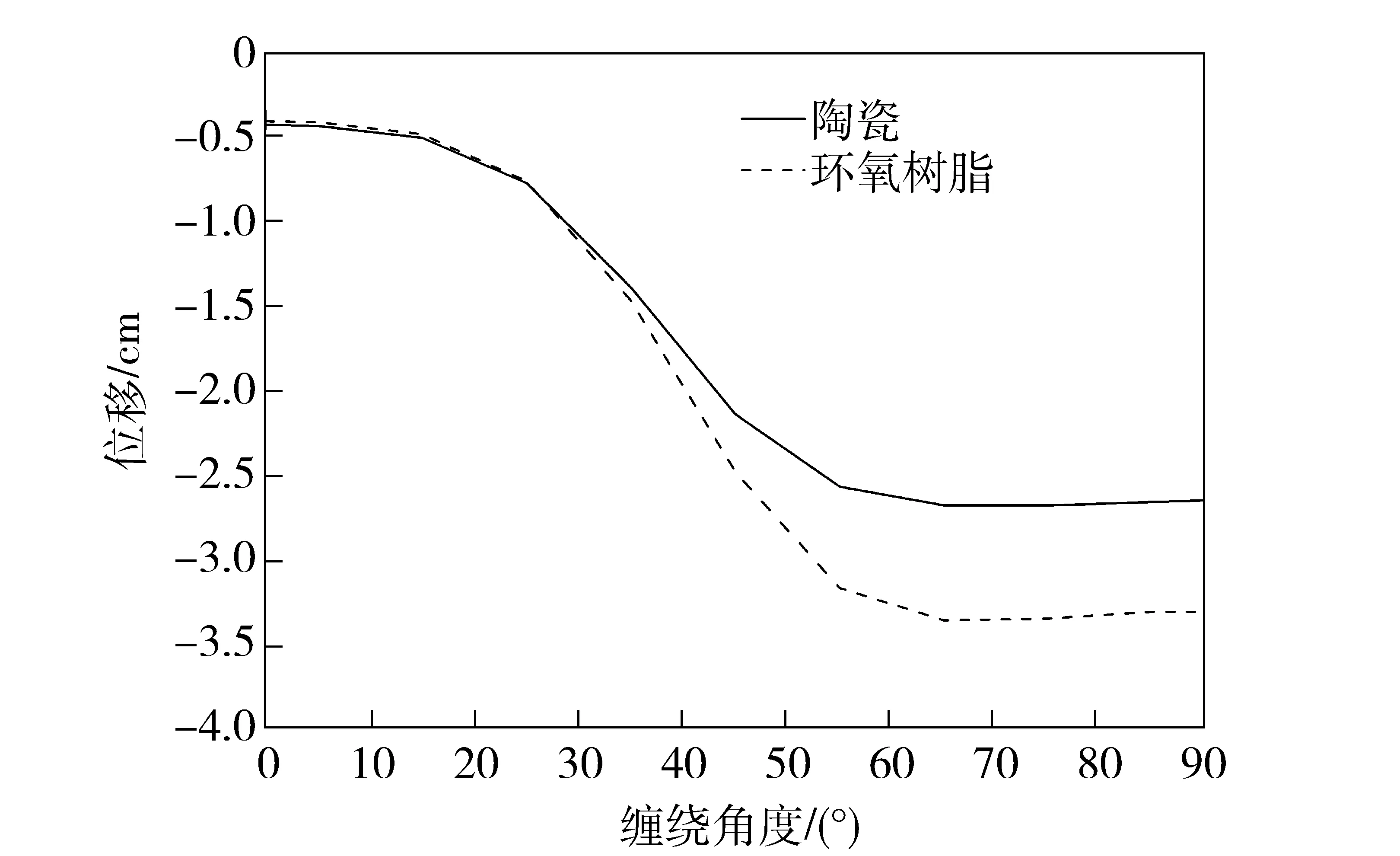
图6 含不同内膛绝缘材料的身管受自重作用下悬臂自由端的位移随缠绕角度的变化Fig.6 Change of displacements of cantilever free top of railgun barrel with different bore insulators with winding angle under gravity

4 结论

本文基于复合材料三维梁理论，建立了电磁轨道炮身管纤维缠绕外壳的抗弯刚度计算模型。根据组合梁的刚度计算法对纤维缠绕的轨道炮身管的整体抗弯刚度进行了分析，并与相应的层合板理论法、有限元法的计算结果进行了比较。结果表明，随着纤维缠绕角度β的变化，3种计算方法所得结果的变化趋势一致，并且计算值在缠绕角度较大时，尤其在β=45°时，一致性相对较好。由于方法1考虑了身管纤维缠绕外壳的三维应变效应，减小了其计算结果与方法3之间的差距，但还是未能综合考虑身管内膛绝缘材料和导轨在内的身管整体的三维应力应变效应。这可为轨道炮身管的初步设计提供一定的参考依据。

此外，本文根据基于三维梁理论所建立的电磁轨道炮抗弯刚度计算模型，分析了纤维缠绕角度对轨道炮身管轴向抗弯刚度的影响，以及不同径向位置的碳纤维缠绕时的缠绕角变化对身管轴向抗弯刚度的影响，并且还对内膛绝缘材料分别为陶瓷和环氧树脂的身管轴向抗弯刚度随缠绕角的变化情况做了分析。结果表明：

1)随着缠绕角度的增大，身管轴向抗弯刚度在缠绕角度较小时，呈明显的下降趋势，在缠绕角度较大时，变化幅度较小，并出现稍微的上升。但缠绕角度对身管径向刚度和强度的影响与对身管轴向抗弯刚度的影响基本相反。由此可见，身管在各方面的力学性能存在相互制约，单纯的调整缠绕角度，其力学性能不能同时得到增强，要根据实际工程需要进行多设计参数的优化调整。

2)缠绕角度较小时，身管抗弯刚度值受内层碳纤维层的缠绕角度影响要比外层碳纤维层的要大，并且计算结果表明，同等条件下，减小内部碳纤维层的缠绕角度可更有效地增加身管抗弯刚度值。

3)随着缠绕角度的增加，内膛绝缘材料分别为陶瓷和环氧树脂的身管轴向抗弯刚度都基本随之减小，由于陶瓷的弹性模量比环氧树脂的高，故而相同缠绕角度下，其身管抗弯刚度也较大。但较小缠绕角度时，陶瓷身管的轴向抗弯刚度随缠绕角度减小而增加的幅度没有环氧树脂身管的大，导致前者的悬臂自由端位移比环氧树脂身管的略大。可见，含高密度高弹性模量的内膛绝缘材料的身管在缠绕角度较小时，减小缠绕角度并不能更好地改善抗弯性能。

References)

[1] Werst M D, Kitzmiller J R, Hearn C S, et al. Ultra-stiff, low mass, electromagnetic gun design[J].IEEE Transactions on Magnetics, 2005,41(1):262-265.

[2] Noel A P, Bauer D P. Laminated barrel axial stiffness assessment[J]. IEEE Transactions on Magnetics, 2001,37(1):454-456.

[3] Geuchy Ahmad M I, Hoa S V. Flexural stiffness of thick walled composite tubes[J].Composite Structure,2016,149: 125-133.

[4] 张恒铭,李峰,潘大荣.基于三维梁理论的复合材料层合管等效抗弯刚度[J].复合材料学报,2016,33(8):1694-1699. ZHANG Heng-ming, LI Feng, PAN Da-rong. Equivalent bending stiffness of composite laminated tube based on the 3D beam theory[J]. Acta Materiae Compositae Sinica,2016,33(8):1694-1699.(in Chinese)

[5] 徐光磊.含内衬纤维复合材料发射筒力学性能研究[D]. 南京：南京理工大学, 2013. XU Guang-lei. Mechanical properties research for fiber reinforced composite launch canister with liner[D]. Nanjing: Nanjing University of Science and Technology, 2013.(in Chinese)

[6] Xia M, Takayanagi H, Kemmochi K. Bending behavior of filament-wound fiber-reinforced sandwich pipes[J]. Composite Structures, 2002,56: 201-210.

[7] Shadmehri F, Derisi B, Hoa S V. On bending stiffness of composite tubes[J]. Composite Structures, 2011, 93:2173-2179.

[8] Kim C, White S R. Analysis of thick hollow composite beams under general loadings[J].Composite Structures,1996, 34:263-277.

[9] Sungsoo N. Control of dynamic response of thin-walled composite beams using structural tailoring and piezoelectric actuation[D]. Blacksburg, Virginia, US: Virginia Polytechnic Institute and State University, 1997.

[10] Zhang C, Wang S. Structure mechanical modeling of thin-walled closed-section composite beams. Part 1: single-cell cross section[J]. Composite Structures, 2014,113:12-22.

[11] 孙华东,林玉祥.复合材料迭层板等效模量的计算分析[J].太原机械学院学报,1993,14(2):113-120. SUN Hua-dong, LIN Yu-xiang.Computation and analysis of equivalent moduli for composite laminations[J]. Journal of Taiyuan Institute of Machinery,1993, 14(2):113-120. (in Chinese)

Analysis of Bending Resistance of Composite Barrel for Electromagnetic Railgun Based on 3D Beam Theory

YIN Dong-mei, XIAO Hong-cheng, LI Bao-ming

(National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

An estimation model of effective bending stiffness for filament-wound composite housing of circular railgun barrel is established based on the 3D composite material thick beam theory. Some effects of beam, such as the three-dimensional strain and warping, are considered in the proposed model. The calculation method of effective bending stiffness of composite beam is used to analyze the bending stiffness of the whole filament-wound composite barrel for railgun. The results are compared with those obtained by laminated plate theory and finite element method. The result shows that the calculated results of the three methods have good consistency for bigger winding angle. The effects of the winding angles of fibers and carbon fibers in different radial positions and the different bore insulators on the bending stiffness of barrel are studied. The research result reveals that the bending stiffness of barrel obviously drops with the increase in winding angle while the winding angle is smaller. The winding angle of inner carbon fiber layers has a great effect on the bending stiffness compared with outer carbon fiber layers. The bore insulator with high density and high elastic module can’t always enhance the bending stiffness of barrel.

ordnance science and technology; 3D beam theory; electromagnetic railgun; barrel; laminated plate theory; bending stiffness

2016-12-07

尹冬梅(1981—)，女，讲师。E-mail:dongmeiyin2010@163.com

TJ866

A

1000-1093(2017)08-1476-07

10.3969/j.issn.1000-1093.2017.08.003