某商业钢连桥结构设计

文｜中国中元国际工程有限公司 王泽 罗佑新 马瑞嘉；北京中外建工程管理有限公司 曹海明

1 工程简介

某地块商业金融项目，位于北京丰台区，北邻五圈路，东邻国际汽车博览中心东路，南邻五圈南路，西邻国际汽车博览中心西路。该项目由商业连廊、两座连桥、展厅入口组成。其中连桥长48米，高6.8米；桥面宽度5.3m；柱中心至悬挑端距离为10.8m，中部跨度为26.4m。树形柱端距悬挑端8.8m，树形柱中部跨度为22.4m，如图1，图2所示。

2 结构设计

为了保持连桥美观，不在桥身设置排水点，水流延桥体长向汇集到邻近建筑物组织排水。因此，找坡面层较厚，最厚处为250mm，最大恒荷载为5KN/m2，考虑周边扶手及装饰造型的重量，恒荷载输入值为 4KN/m2～6KN/m2；活荷载 ：3.5KN/m2。同时，由于建筑美观及桥下需通行消防车的使用要求，限制结构梁高不超过800mm，跨中高跨比为1/30，悬挑端为1/10。基本风压0.45KN/m2，地震烈度8度，场地分组二组3类如图3。

桥身的结构选型首先想到的是常用的梁板体系，主要受力构件为三根截面为800x300x12x20的箱型梁；整座桥面通过树形柱的8个支点支撑于底部圆柱上。树型柱截面为450/300x30；底部圆柱截面为1200x30（如图4）。整个桥面最后仅由底部两根圆柱支撑，所受荷载较大，为了保持其具有足够的刚度及稳定性，管内灌注C40无收缩自密实混凝土。利用MIDAS8.36进行结构计算分析，结果如下。

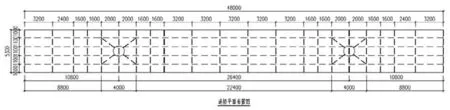
图1

图2

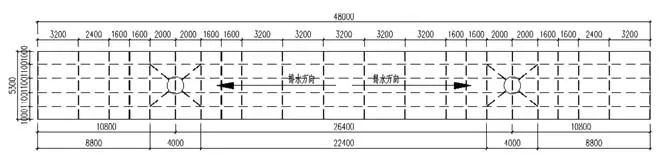
图3

包络工况下，应力比最大的构件为与树形柱端连接的箱型梁，应力比为0.597（如图5）。在恒+活标准荷载工况下，跨中部分竖向最大位移为：56.754mm，挠跨比为1/395，不满足限值1/400的要求；悬挑端最大位移为63.973mm，挠跨比为1/275(计算时按规范要求取悬挑长度2倍)，依然不满足规范1/400的要求（图6）。通过计算可知强度较富裕，但刚度需要起拱来满足限值要求。本工程连桥连接两端展厅商业及高端酒店，人流量大，且跨度较大，在设计过程中不仅需要对强度和刚度进行有效控制，更需要对连桥进行舒适度分析。根据《楼板体系振动舒适度设计》1及《高规》2的相关介绍，人行天桥舒适度应满足如下要求：

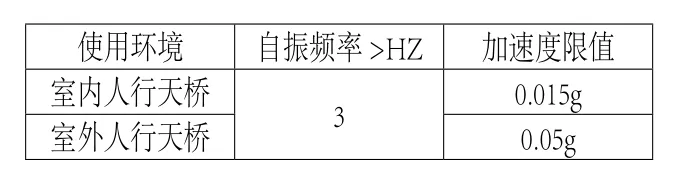
使用环境 自振频率>HZ 加速度限值室内人行天桥 3 0.015g室外人行天桥 0.05g

室内人行天桥与室外人行天桥控制标准的差别主要由于周围环境的差异所造成人对振动敏感程度的不同。室内较为安静，行人更容易受到振动的影响，室外较为嘈杂，行人对舒适性的敏感程度会有所降低。本工程连桥虽然为室外连桥，但三面均为建筑物，且位于同一建筑群内，处于较为封闭的状态；连接的商业展厅与酒店规格较高，因此此处以室内人行天桥控制标准为依据来设计。

图4

图5

图6

图7

图8

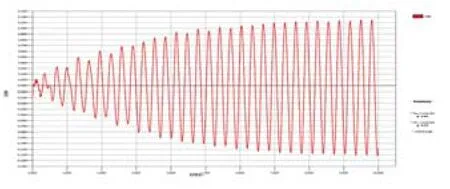
图9

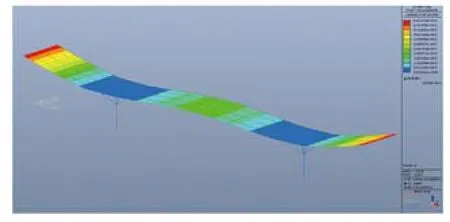
图10

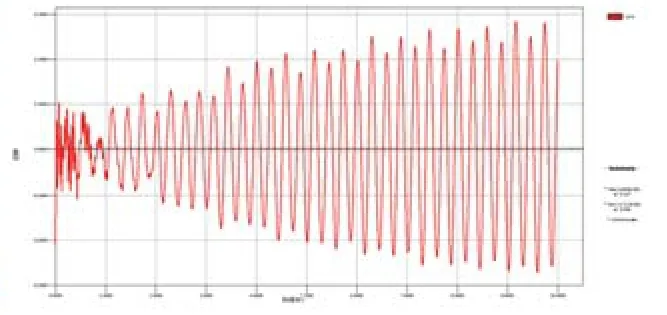
图11

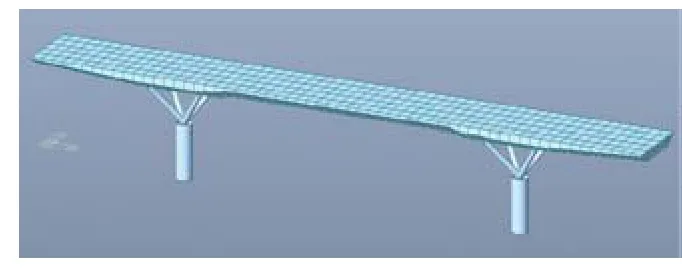
图12

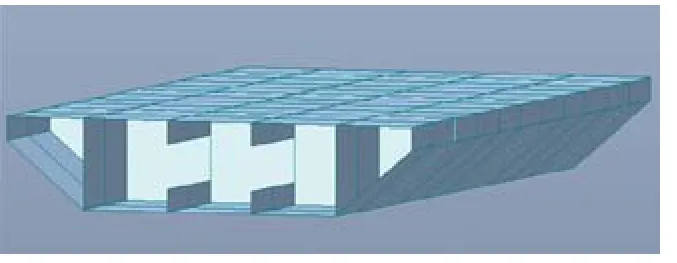
图13

图14

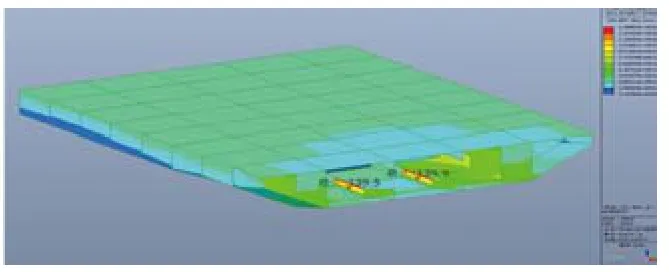
图15

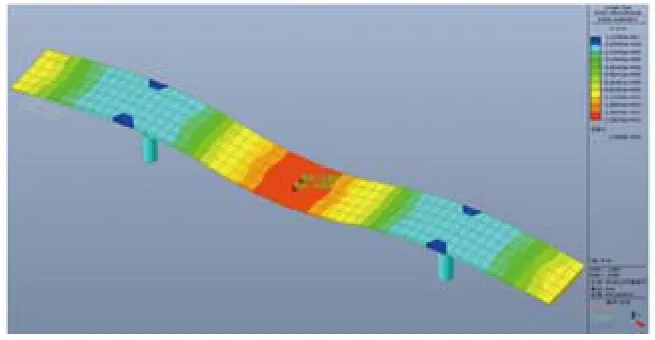
图16

图17

楼板体系的第一阶自振频率对应的能量最大，在振动舒适度分析时，楼板体系的第一阶竖向自振频率是最重要的。随着共振频率的增大，其对应的能量逐渐减小。

为了更准确计算桥面体系动力响应，采用有限元分析法，考虑前三节行走荷载的影响，荷载函数可表示为：

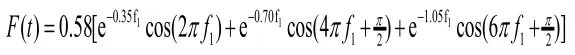
恒荷载取面层及自重，与静力计算取值相同；对于连桥，附加活荷载很小，所以不考虑附加活荷载的影响。阻尼比取0.01。利用MIDAS.GEN.6.36对结构进行模态及时程分析。计算结果如下：

上图为跨中最不利点计算结果。通过对结构进行模态分析，得到跨中第1竖向自振周期为0.3138s，第1自振频率为3.1867HZ，最不利点为2368点，如图所示。将第1自振频率值带入荷载函数得到人连续行走激励荷载，在最不利点施加节点动荷载，进行时程分析，得峰值加速度为：0.1142m/s-2，即0.0114g，自振频率与峰值加速度都接近规范限值要求。

悬挑端第一竖向自振周期为0.2865s，第一自振频率为3.4904HZ，最不利点为2375点，如图所示。人走路的频率在1.6～3.2HZ范围内，因此激发楼板竖向共振的频率应为1.7452HZ，计算得峰值加速度为：0.2844m/s-2，即0.02844g。频率满足要求，加速度峰值已超限值要求0.015g。

为了满足连桥舒适度的要求，需加大连桥刚度或减小连桥质量。为了充分利用桥面宽度，将桥身设计为宽度为5300mm的箱形腔梁，中部设置加劲肋，以满足宽厚比要求，减小板厚。利用壳单元建立模型，壳厚度为16mm，下部竖向构件与前相同，如图12，图13。

计算结果如下：

桥面最大应力为139.86MPa,为支座附近加筋肋，应力水平较低（如图14，图15）。

在恒+活标准荷载工况下，跨中部分竖向最大位移为：15.503mm，挠跨比为1/1449（如图16）；悬挑端最大位移为10.308mm，挠跨比为1/854(计算时按规范要求取悬挑长度2倍，如图17)。挠跨比满足规范要求，刚度显著增大。

悬挑端第一竖向自振周期为0.1470s，第一自振频率为6.8027HZ，最不利点为2778点，如图18。激发竖向共振的频率应为2.2676HZ，在最不利点2359点施加时程荷载，计算得此频率激励下，楼板峰值加速度为：0.0881m/s-2，即0.0088g(如图19)，频率与加速度限值都满足规范要求。跨中最不利点自振频率远大于3HZ，不必要进行加速度峰值验算。

3 关键节点设计

3.1 树形柱球节点

由于整个桥面通过树形柱传递给下部钢管混凝土柱，保证树形柱根部的节点传力可靠对于整个桥体的安全至关重要。树形柱根部构造如图20、21所示：

四根树形柱通过一个半球节点连接于下部钢管混凝土柱，沿四支分叉方向设置两道拱性加劲肋，用来传递树形柱的轴力以及加强球节点刚度。在球节点与下部柱连接处及拱形加劲肋底部设置两道水平加劲肋，中部开洞，使混凝土浆体可到达球节点顶部，并开适量排气孔，如图20。MIDAS计算模型读取树形柱计算结果为轴力970KN，树形柱两个方向弯矩分别为260KN.M，170KN.M。使用Abaqus6.14-1对球节点进行计算分析

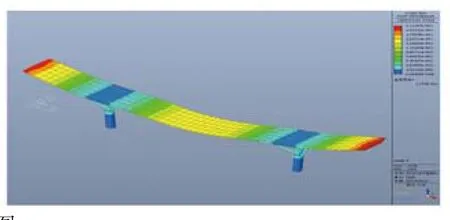
图18

图19

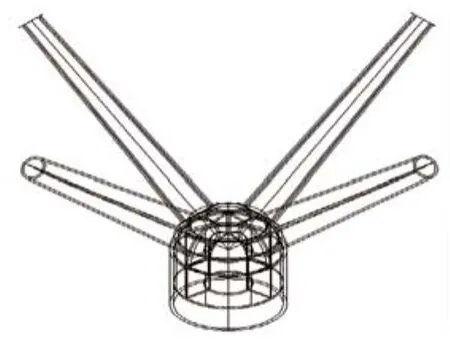
图20

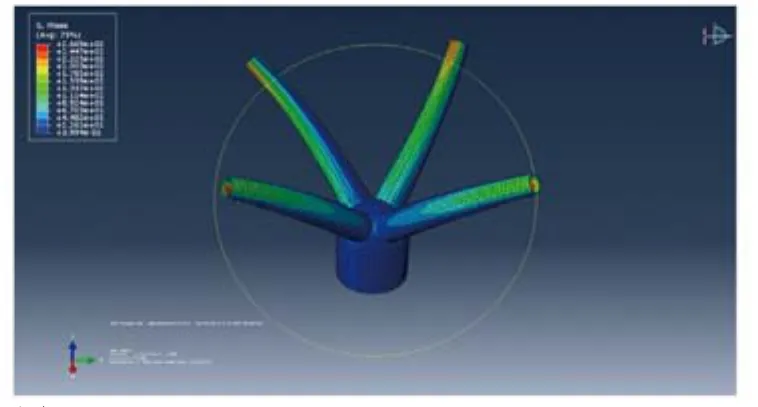
图21

图22

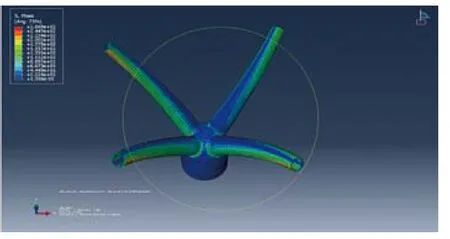
图23

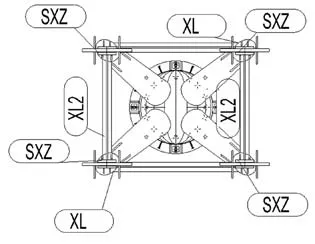
图24

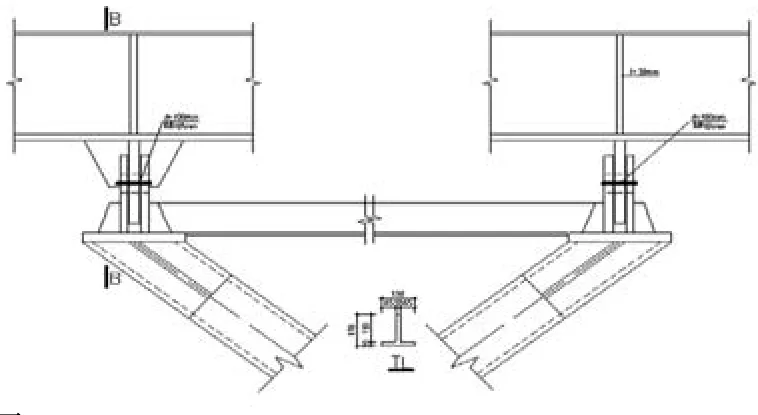
图25

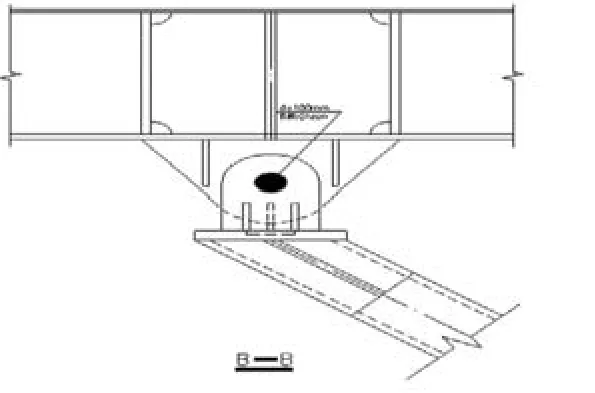
图26

计算结果显示树形柱根部节点应力最大值133.7MPa，最大应力比0.50；球节点应力最大值89.24MPa，最大应力比为0.37（如图21）。树形柱端部应力水平较高是因为在端部建立了刚性面，用于施加荷载，出现了应力集中,此处应力不具参考意义。此外，内灌混凝土的主拉应力为3.586MPa，超过了C40混凝土的抗拉应力1.71MPa，混凝土会开裂（如图22）。开裂后，球节点将承受更大荷载，因此需要验算球节点内不填充混凝土应力分布情况。

如图23，内部不填充混凝土时，树形柱根部节点应力最大值155.7MPa，最大应力比0.53；球节点最大值155.7MP，最大应力比0.59。球节点强度满足要求。

3.2 树形柱与桥身连接节点

树形柱与桥身的计算假定为铰接连接，且轴力接近1000KN，轴力较大，选用销轴连接。

图24所示为树形柱俯视图，主耳板连接于桥面，两块次耳板连接于树形柱顶端，销轴方向平行于桥面宽度方向。主次耳板处均有加劲肋保持耳板的平面外稳定。连接桥身的主耳板开长圆孔释放温度应力。四根树形柱在柱顶以XL相连，XL作用详见四：XL（系梁）作用。图25，图26为节点立面与剖面。

销轴材质采用40Cr，其抗拉强度为1000MPa；屈服强度800MPa；抗剪强度为其屈服强度的0.5～0.7倍，此处取抗剪强度为400MPa。经计算销轴抗剪，抗弯，抗压及组合应力后，采用直径为100mm的销轴可满足要求。耳板材质均为Q345B，经计算耳板抗剪，承压及劈裂破坏，确定主耳板厚度为50mm，两块次耳板分别厚为30mm，40mm。

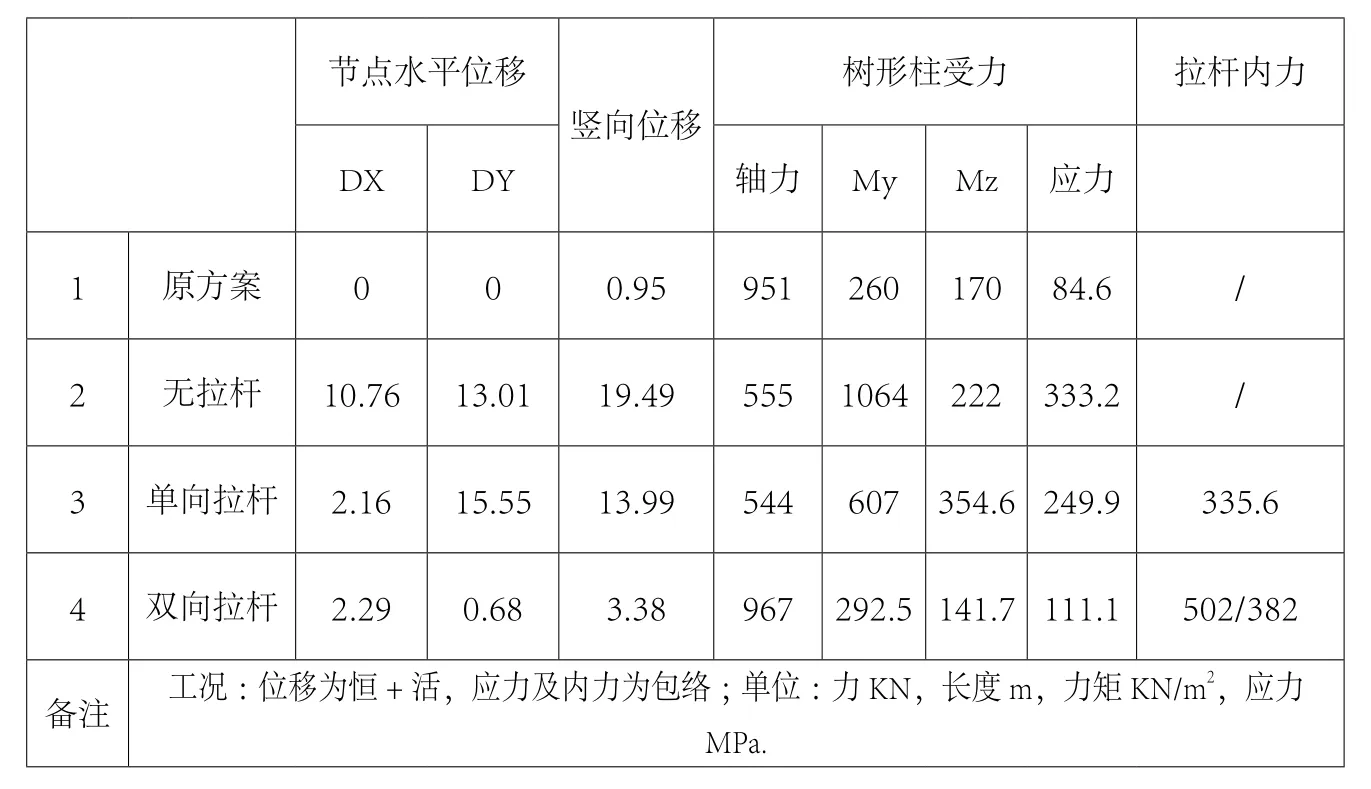
节点水平位移树形柱受力 拉杆内力DX DY 轴力 My Mz 应力竖向位移1 原方案 0 0 0.95 951 260 170 84.6 /2 无拉杆 10.76 13.01 19.49 555 1064 222 333.2 /3 单向拉杆 2.16 15.55 13.99 544 607 354.6 249.9 335.6 4 双向拉杆 2.29 0.68 3.38 967 292.5 141.7 111.1 502/382备注 工况：位移为恒+活，应力及内力为包络；单位：力KN，长度m，力矩KN/m2，应力MPa.

4 系梁（XL）的作用

进行连桥静力计算及抗震计算时，树形柱与连桥的连接方式为铰接。原方案中Midas模型铰接模拟方式为连桥与树形柱端共用节点，直接相连，并释放节点弯矩。此时连桥与树形柱无相对节点位移；树形柱的四枝虽没有建立系梁连接，实质上桥身的巨大刚度对树形柱有很强的拉结作用。使用销轴节点的实际情况为桥身与树形柱端由于销轴的节点做法而产生了520mm的高差，且在节点高度中部由销轴铰接，在竖向荷载作用下，树形柱端与桥身会产生相对位移。同时由于中部销轴的存在，实际中桥身对树形柱也没有拉结作用，此时与模型假定不相符。系梁的作用即为替代桥身，对树形柱进行拉结，减小节点位移，平衡部分由竖向荷载对树形柱产生的弯矩，使实际做法与模型假设最大限度吻合，整个设计成立。下图为按照节点实际高度建立模型，上下耳板连接处铰接。

计算结果如下：

从上表看出，2与1相比，由于销轴节点的做法与原方案假设的不同，对于树形柱内力分布有很大影响，与原方案相比，轴力减小，My为原方案5倍，若按此内力设计，原球节点做法承载力不满足，将会导致整个结构设计不成立；3与2相比可看出，拉杆对于限制水平节点位移作用非常明显，也能有效减小该方向弯矩；4与1相比，双向拉杆计算结果与原模型计算数值比较接近。按照4的内力符合球节点承载力，满足要求。

5 结语

原方案

无拉杆

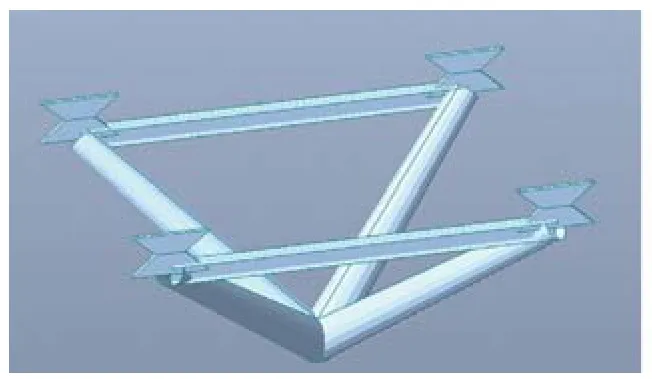
单向拉杆

双向拉杆

通过对钢连桥的强度，刚度以及舒适度的计算，选择了箱型腔梁作为桥身的结构方案。对于大跨钢连桥，舒适度计算必不可少，有时起控制作用；连桥舒适度不满足时，可以减小自重或提高刚度，必要时可加阻尼器；节点设计完成需核对是否与整体模型的边界条件假定相符，若不相符，需采取必要措施，使其与原结构强度，刚度等效，否则将导致巨大安全隐患。