借助数形结合 提高课堂实效

◎余彩芳

借助数形结合 提高课堂实效

◎余彩芳

《义务教育数学课程标准（2 0 1 1年版）》指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中发挥着重要作用。”教学中，可借助几何直观，帮助学生理解概念、理解算理与算法、理清数量关系、分析并解决问题等，努力提高课堂教学效果。

一、借助数形结合，帮助学生理解概念

在小学低年段对于概念的硬性规定很少，因为对低年级的学生来说，许多数学概念比较抽象，很难理解，特别需要直观的视觉效应。因此，可以借助“数形结合”思想的进行帮助教学，通过对图形的分析，帮助学生理解数学概念。

如在教学“认识倍数”一节课时，可以创设游玩动物园的情境。动物园里有6只小鹿，3只小猴，小鹿的只数是小猴的几倍？让学生尝试用自己喜欢的图形画一画，圈一圈,来表示6是3的几倍？然后再指名汇报，出现如下情况。

通过画图，学生很直观地看出6里面有2个3，也就是说6是3的2倍。这样，为抽象的倍的概念建立了具体形象的表象，理解起来就会容易得多。以后在学习较复杂的“和倍、差倍”问题时，学生会很容易想到画直观图帮助解决问题。

二、借助数形结合，帮助学生理解算理

数形结合是一种非常重要的思想方法，它倡导通过数与形的相互转化、彼此参照，以“代数问题几何化”或“几何问题代数化”来促进数学理解、数学问题解决。借助数形结合的核心是“借形思数”。因此，在教学中，教师应充分应用数形结合的思想，引导学生依托鲜活的“形”去思考凝练的“数”，帮助学生理解算理。

如在教学“两位数乘两位数”时，可以把枯燥的算式与图形联系起来,利用图形的直观帮助学生理解算理。在探索1 4×1 2的计算时，教师采用课本上直观的点子图，让学生自已动手实践，在点子图上画出自已的思考过程。学生在图中充分展示了自已的思维过程，呈现出不同的算法：1 4×6×2=，1 4×4×3=，1 4×1 0+1 4×2=，1 0×1 0+1 0×4+2×1 0+2×4=，等。并在探索竖式计算时，紧密结合点子图，让学生指出1 4×2=2 8、1 4×1 0=1 4 0、1 4 0+2 8=1 6 8分别在图上的哪里。结合点子图让学生说一说1 4 0的4为什么写在十位上，1为什么写在百位上。借助直观手段把点子图与口算、竖式计算有机结合起来，沟通它们之间的联系，有效地突破了本课的教学难点，使学生很好地理解了计算的算理。（图1）

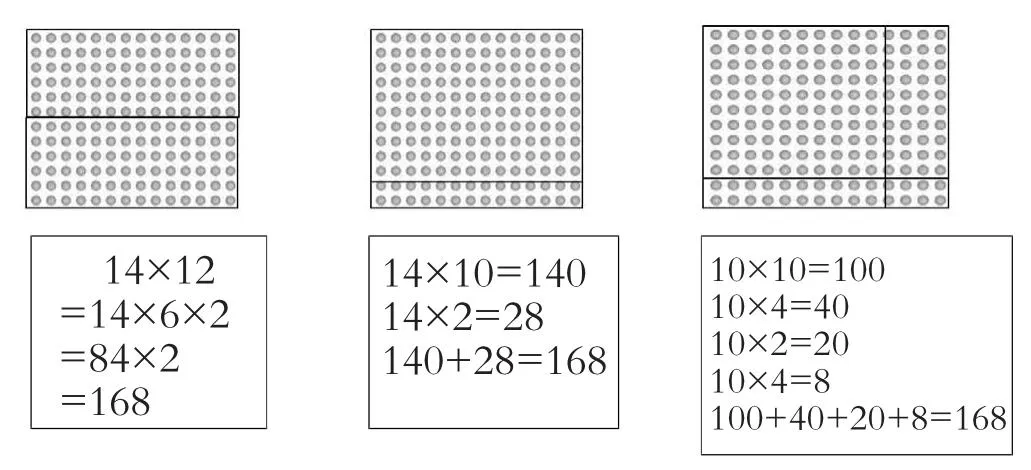
图1

应用数形结合的思想，将许多抽象的数学计算变成可操作过程，使抽象的算理变成了形象化、简单化，使学生表象清晰，记忆深刻，是形象图形与抽象算理相融合的过程，这就是数形结合的魅力所在。

三、借助数形结合，帮助学生掌握算法

算理就是计算方法的道理，传统的计算教学往往“只重视算法而忽视算理”，时下，计算教学应做到“法理并重”，即要在理解算理的基础上掌握计算方法，又要在掌握算法基础上懂得算理，正所谓“知其然、知其所以然。”而算理往往是比较抽象的，应借助数形结合的帮助，使学生正确理解算理。通过直观操作，以形助数，使抽象的算理形象化，具体化。

如在教学“9+几”一节课时，先出示情境图，让学生收集信息，提出问题并列出算式，即：算式9+4=，引导学生用小棒、圆片等实物操作来感知“凑十法”的过程，进而理解“凑十”的算理。先出示空白格子图，学生在格子里面摆9个圆片，外面放4个圆片。先通过观察，再动手“拿”，从外面拿1个放进格子里，这样格子里就“凑”成1 0个圆片，外面还有3个，“合拼”起来就是1 3个圆片。在“拿”的基础上进行感悟，把4分成1和3，1和9凑成1 0，1 0加3就等于1 3。最后，引导学生用自己的语言来描述“拿、凑、合”的过程。（图2）

图2

这样，学生能很好的理解“凑十法”的含义，并在动手操作中，体验计算过程，从而掌握了“凑十法”，也为后续学习打下坚实基础。

四、借助数形结合，帮助学生理清关系

分数问题、比的问题比整数问题显得更加复杂和抽象，许多学生在解答这类问题时，思路单一，缺少变通能力，学生的学只是机械套用公式，缺乏一定的空间观念，解题时重“数”而轻“形”解题思路不灵活。我在教学时注重引导学生画图，变抽象为直观，培养学生学习数学能力，提高课堂教学的有效性。

如在教学“比的应用”时，出示这样一道题：（以下称原题）

调制巧克力奶，巧克力与奶的质量比是2∶9。淘气有巧克力660克，都用来调巧克力奶，他要准备多少克奶？

学生受上节课的影响，把4 4 0看成了总数，列式：6 6 0÷（2+9）×9或6 6 0× 。如果学生在解题时能画图分析就会避免这样的错误。（图3）

图3

图4

6 6 0是巧克力占2份，先求一份6 6 0÷2=3 3 0克，奶9份就用3 3 0×9，所以列式为6 6 0÷2×9。并把这题与另外一道题进行比较。（以下称附加题）

调制巧克力奶，巧克力与奶的质量比是2∶9。淘气要调制出660克的巧克力奶，他要准备多少克奶？（图4）

通过画图直观地看出原题6 6 0是巧克力占2份，附加题的6 6 0是巧克力奶占1 1份，很清楚地分辨出这两题的异同。从图中还可以知道原题奶的质量是巧克力的，算式6 6 0×巧克力的质量是奶的，算式6 6 0÷，巧克力的重量占巧克力奶的，先求巧克力奶，再求奶，算式6 6 0÷-6 6 0。这样，利用直观图把比与分数紧密联系，学生思路灵活，解题方法多样法，发展了学生的思维。

五、借助数形结合，帮助学生解决问题

直观图的恰当使用，不但可以帮助学生发现并理解数学问题，而且有利于他们掌握数学学习的方法。尤其碰到比较抽象、关系复杂的问题时，运用直观图能够开拓学生的解题思路并使解题简捷明快。

如在教学用分数解决问题时，出示这样一道题：一段公路已修了它的后还剩下4.8千米，问修了多少千米。一般用分数应用题的解题方法，应该先分析单位“1”的量是这段公路的长度，而后找到剩下的4.8千米和其所对应的分率再求出这段公路的长度，最后算出修了多少千米。列综合式：4.8÷（1-）-4.8，基于这样的思考，问题解决需要三步计算，思路繁琐。而运用几何直观，鼓励学生画线段图，清楚地建立了分数和图形、分数和比之间的关系，显示了已修的和剩下的之间的数量关系，从中凭直觉一眼就“看出”已修的是剩下的3倍，即4.8× 3=1 4.4（千米），从而简洁而又创造性地解决了这道较复杂的分数问题。（图5）

图5

通过画图，使题目更直观，原来在题目中学生不容易理解的一些数据都能很好地在图中得到分析，从而使学生体会用图解题的直观、形象，能很好帮助学生理解题意，解决问题。

（作者单位：福建省福清市玉屏中心小学）

（责任编辑：杨强）