基于Patran及频域分析的叠层焊点随机振动可靠性分析

张 龙， 黄春跃， 黄 伟， 华建威

(桂林电子科技大学 机电工程学院， 广西 桂林 541004)

基于Patran及频域分析的叠层焊点随机振动可靠性分析

张 龙， 黄春跃， 黄 伟， 华建威

(桂林电子科技大学 机电工程学院， 广西 桂林 541004)

基于Patran软件建立了叠层焊点三维有限元分析模型，分析了随机振动条件下叠层焊点的固有频率、振型和频率响应规律，获得了叠层焊点应力应变分布和应变功率谱密度响应曲线，并基于功率谱和雨流计数法计算出了叠层焊点振动疲劳寿命；分析了焊盘直径和焊点最大径向直径对叠层焊点随机振动寿命影响。仿真结果表明：在叠层焊点高0.5 mm、焊盘直径0.3 mm和焊点径向最大直径0.4 mm时其随机振动疲劳寿命为3 132 h；当焊盘直径从0.2 mm增加到0.35 mm时，叠层焊点振动疲劳寿命随焊盘直径增大而增大；当焊点最大径向直径从0.4 mm增加到0.55 mm时，叠层焊点振动疲劳寿命随焊点最大径向直径增大而减少。

随机振动；叠层焊点；功率谱；疲劳寿命；有限元分析

球栅阵列(Ball Grid Array, BGA)焊点起着电气连接、机械支撑及传热作用，在倒装芯片封装中占有举足轻重的地位。为了提高BGA焊点的热疲劳寿命，一是尽可能增加焊点高度，二是在芯片下填充树脂。采用叠层焊点的方式即可使焊点高度大大增加，从而提高焊点可靠性[1]。针对叠层焊点热疲劳寿命，Yan等[2]制作了双层锡铅焊料焊点，经热循环冲击实验证明该种双层焊点的可靠性是常规单层焊点的1.5倍；Keser等[3]制作了双层焊点并在-55～+125 ℃条件下经1 000周热循环加载测试证明双层焊点均无失效产生；Son等[4]对Cu/SnAg叠层焊点进行了1 000周的热循环加载测试均无失效产生；韦何耕等[5]研究发现与单层焊点相比焊点叠加方式能有效提高焊点热疲劳寿命。这些研究都证明了采用焊点堆叠设计可以有效延长焊点热疲劳寿命。

除了热疲劳，焊点寿命还受振动疲劳影响，据美国空军统计，超过20%的电子器件是由于振动导致失效的[6]。虽然振动冲击引起的焊点可靠性问题日益引起人们的重视，但国内关于单层倒装焊点随机振动的研究仍然不多，而对于叠层焊点随机振动展开研究则更少，国内学者中仅黄春跃等研究了PBGA结构方式、焊点材料、底充胶弹性模量和密度对叠层无铅焊点随机振动应力应变的影响；Shao等[7]研究了随机振动条件下焊点高度、直径对叠层金凸点应力应变的影响。但是，这些研究仅针对叠层焊点内的随机振动应力应变，而未研究随机振动应力应变对焊点随机振动寿命的影响。正是鉴于叠层焊点相对于单层焊点所具有的优良热疲劳寿命，文中以叠层焊点为研究对象，对其随机振动疲劳寿命进行分析，考察叠层焊点几何结构参数对其随机振动寿命的影响，以达到进一步提高叠层焊点振动可靠性的目的。

1 叠层焊点随机振动有限元分析

1.1 叠层焊点三维有限元模型

文中研究对象为带有叠层焊点的倒装芯片，将其组装于印制电路板(Printed Circuit Board, PCB)上，模型实体来源于TopLine 公司生产的8 × 8 全阵列产品，共64个叠层焊点，焊点间距为0.8 mm。所选取的叠层焊点材料为有铅焊料Sn63Pb37。采用软件Patran建立的叠层焊点随机振动三维有限元分析模型如图1所示。模型中PCB尺寸为70 mm×70 mm×1 mm,芯片尺寸为8 mm×8 mm×0.2 mm，叠层焊点高为0.5 mm,焊盘直径为0.3 mm，焊点径向最大直径为0.4 mm 。模型网格划分中单元是六面体单元Hex，使用的是映射网格生成器IsoMesh，整个模型共划分39 264个单元，44 232个节点。对模型施加的位移约束条件为：约束PCB底面四个角点的六个自由度。模型中各部分的材料参数如表1所示。

材料名称弹性模量E/GPa泊松比μ密度ρ/(Kg·m-3)芯片1300．282320PCB板18．20．251800焊点35．30．358420

文中采用的随机激励的形式为加速度功率谱密度 (Power Spectral Density, PSD)，来源于美国军用标准MIL-STD NAVMAT P-9492。加速度功率谱曲线在随机振动频率在20～80 Hz时曲线上升斜率为+3 dB/oct，对应的加速度功率谱密度幅值范围为0.01～0.04 g2/Hz，80 Hz时为0.04 g2/Hz；当随机振动频率在80～350 Hz时，对应的加速度功率谱密度幅值为0.04 g2/Hz，当随机振动频率在350～2 000 Hz时，曲线以-3 dB/cot的斜率下降，对应的加速度功率谱密度幅值范围为0.04～0.01 g2/Hz。

1.2 模态分析

(a)第1阶模态及其叠层焊点形变

(b)第2阶模态及其叠层焊点形变

(c)第3阶模态及其叠层焊点形变图2 叠层焊点有限元模型前3阶振型Fig.2 Vibration mode of first three orders within finite element model of BGA package

阶次1234频率/Hz260．4534．5669．01298．1阶次5678频率/Hz1413．81554．02134．02475．7

文中随机振动分析的频率范围是20～2 000 Hz，从表2可见，该模型的前6阶模态的固有频率均处于20～2 000 Hz这一频率范围，所以，在20～2 000 Hz频率范围的随机载荷下，该模型只发生前6阶模态振动弯曲变形(前3阶振型如图2(a)～图2(c)所示)。从图2可知，第1阶模态下，PCB板的中心有较大振幅，带动整个板向下凹或上凸，倒装芯片及叠层焊点完全处于模型弯曲变形较大的区域；第2阶和第3阶模态下，PCB板四周振幅较大，中心振幅较小，倒装芯片及叠层焊点大部分处于模型变形较小的区域。所以，随机振动条件下，第1阶模态将对叠层焊点的随机振动可靠性产生较大影响。

1.3 频率响应分析

频率响应分析用于计算结构在振动载荷作用下对每一个计算频率的动响应。在模型正下方基础点与模型四个角点之间建立多点约束MPC(Multi-Point Constraint),其中四个角点的六个自由度都与基础点关联，对模型基础点施加在20～2 000 Hz内振动量为1的单位载荷，如图3所示。设置模态阻尼为0.01[8]，经频率响应分析，模型拐角处受力较大的叠层焊点中变形最大的第20号单元应变响应曲线如图4所示。

图3 带随机基础激励的基础点的模型Fig.3 Model with basis point

图4 变形最大的第20号单元应变频率响应曲线Fig.4 Curve of strain frequency response within unit No.20 with the maximum deformation

由图4可知，在20～2 000 Hz频率范围内振动量为单位载荷作用下，260.4 Hz和1 413.8 Hz频率下应变频率响应曲线有明显尖锐峰值，且260.4 Hz下峰值明显高于1 413.8 Hz下峰值，因此在260.4 Hz时叠层焊点随机振动响应的应变最大。而由表2可知，260.4 Hz是第1阶模态的固有频率、1 413.8 Hz是第5阶模态的固有频率。这说明了第1阶模态和第5阶模态将对叠层焊点的随机振动可靠性产生较大影响，而以第1阶模态对叠层焊点的随机振动可靠性产生的影响为最大，频率响应分析结果验证了上节模态分析的结果。

1.4 随机振动分析

在随机激励为前面所述PSD的随机振动条件下，叠层焊点阵列的应变响应分布如图5。从图5见，应力应变从内部到外部逐渐增大，出现最大应力应变的叠层焊点位于焊点阵列的四个拐角处。这是因为构件沿垂直板面方向振动时，芯片与PCB发生弯曲变形，叠层焊点外围受到变形比中心的大，即距离中心越远，受到的变形越大。焊点的最大应变位于与芯片或PCB板连接面区域离中心最远处，最大等效应力为19.9 MPa，最大等效应变为5.08×10-4。

图5 叠层焊点阵列应变响应分布Fig.5 Strain distribution within stacked solder joint array equivalent

基于Patran软件可得到危险焊点应变最大单元的功率谱密度曲线，再基于功率谱密度即可估算出所分析构件局部危险部位的疲劳寿命。叠层焊点内应变最大单元的应变功率谱密度曲线如图6所示，该曲线表示在各个频率下响应的应变功率的线密度值。从图6中可以看出在260.4 Hz和1 413.8 Hz这两个频率下有明显峰值，代表这两个频率下响应的应变功率较高。此曲线下覆的面积的极限为振动过程中的平均功率值，即为均方值。图6所示曲线的均方根值RMS(Root Meam Square)经计算为3.659×10-4。

(3)神经网络的训练需要采集大量的有效数据，以保证输出的结果更具有准确性，而在实际情况中，由于实际条件限制，收集到的训练样本和测试样本都存在着局限性，故有待进一步提高。

图6 应变功率谱密度响应曲线Fig.6 curve of strain power spectral density response

1.5 叠层焊点随机振动疲劳寿命预测

对于叠层焊点随机振动的疲劳寿命可以由得到的应力应变的频域信息转换为时域信息，采用雨流计数法得到载荷幅值的概率密度函数，结合S-N曲线和Miner理论可求出焊点寿命[9]。本文使用应变功率谱密度的周期图法逆向算出频谱的模，相位信息由0～2π上均匀分布产生，组成带相位信息的频谱经傅里叶逆变换得到时域信号。文中取1 s为周期，经转换得到应变时域信号如图7所示。对应变时域信号进行雨流计数得到应变范围分布函数，如图8所示。

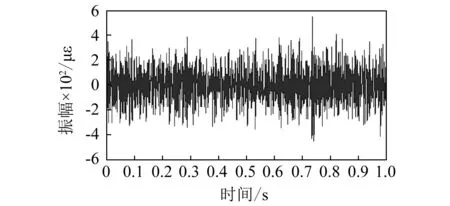
图7 经傅里叶逆变换得到时域信号Fig.7 A time-domain signal by inverse Fourier transform

图8 应变范围分布函数Fig.8 Distribution function of strain range

电子封装器件焊点由机械振动引起的失效，是由弹性形变引起的高周疲劳产生的[10]，所以可以忽略Manson-Coffin经验公式中塑性项,其关系式为

(1)

式中:Δε为总的应变范围；E为弹性模量；σf为应力强度系数；b为疲劳强度指数；Nf为疲劳寿命。对于Sn63Pb37:σf为155 MPa；b为-0.12；E为35.3 MPa,数据来自文献[11]。

Miner线性积累损伤理论是工程上广泛采用的一种疲劳寿命计算方法。假设需要M个单位时间t,焊点产生失效[12]，则

(2)

式中:ni为单位时间t内某一等效应变εi对应循环次数；Nfi为根据Manson-Coffin经验公式得到的在等效应变εi下实效疲劳次数。因此，总的焊点随机振动疲劳寿命预测值可以用式(3)表示

T寿命=M×t

(3)

由上述流程和公式并经过采用Matlab编程分析计算，可以计算出当焊点高为0.5mm、焊盘直径为0.3mm和焊点径向最大直径为0.4mm时叠层焊点振动疲劳寿命T寿命为3 132 h。

2 结构参数对叠层焊点随机振动疲劳寿命影响

2.1 焊盘直径对叠层焊点随机振动疲劳寿命影响

其他参数不变，改变焊盘直径，分别建立相应的有限元分析模型，研究焊盘直径的变化对叠层焊点随机振动疲劳寿命的影响。取焊盘直径分别为0.20 mm,0.25 mm,0.30 mm和0.35 mm，对相应的模型进行有限元分析并进行随机振动疲劳寿命计算后所得结果如表3所示。从表3中的数据可以看出，随着焊盘直径从0.20 mm增加到0.35 mm时，危险焊点所受的最大等效应力应变减小，叠层焊点振动疲劳寿命随之增大。

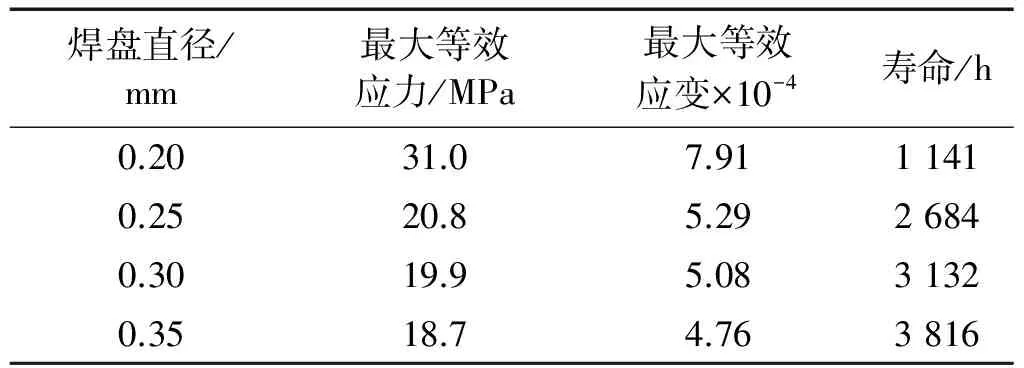
表3 不同焊盘直径时焊点最大等效应力应变和寿命对比

2.2 焊点径向直径对叠层焊点随机振动疲劳寿命影响

其他参数不变，改变叠层焊点的焊点最大径向直径，分别建立相应的有限元分析模型，研究焊点最大径向直径的变化对叠层焊点随机振动疲劳寿命的影响。取焊点最大径向直径分别为0.40 mm，0.45 mm，0.50 mm和0.55 mm，对相应的模型进行有限元分析并进行随机振动疲劳寿命计算后所得结果如表4所示。从表4中计算数据可以看出，随着焊点最大径从0.40 mm增加到0.55 mm时，危险焊点所受的最大等效应力应变增大，叠层焊点振动疲劳寿命随之减小，且焊点最大径从0.40 mm增加到0.50 mm时，虽然最大等效应力应变变化并不大，但寿命值却降幅较高。这是因为影响寿命的因素除了有最大等效应力应变外，还有整个周期不同应力应变值所对应的循环次数。

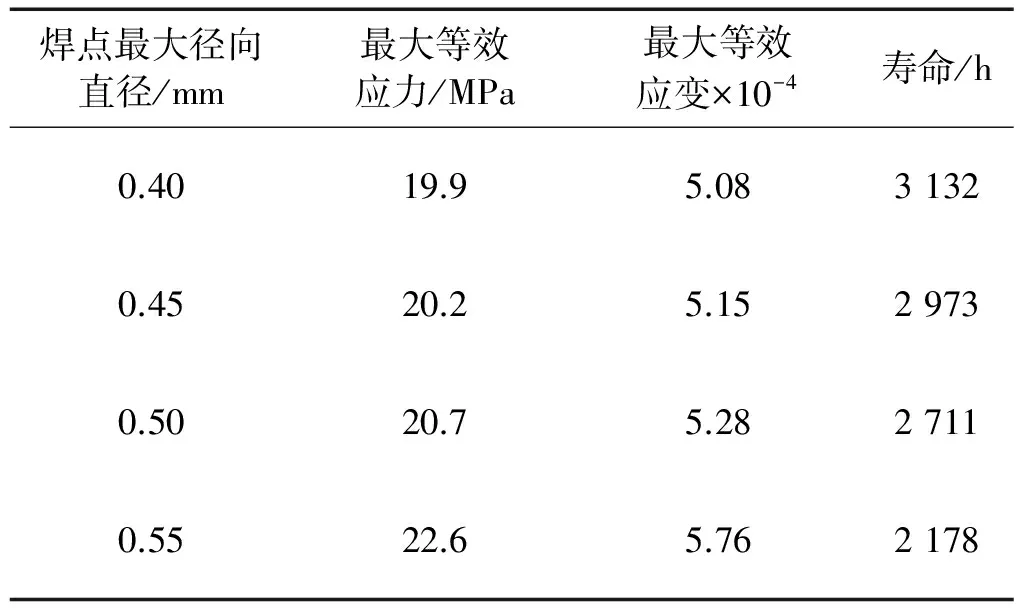
表4 不同焊点径向直径时最大等效应力应变和寿命对比

3 结 论

(1)在随机振动条件下，在焊点高为0.5 mm,焊盘直径为0.3 mm，焊点径向最大直径为0.4 mm的条件下，通过仿真得到叠层焊点振动疲劳寿命为3 132 h。

(2)其他参数不变，焊盘直径从0.20 mm增加到0.35 mm时，叠层焊点所受的最大等效应力应变减小，叠层焊点振动疲劳寿命随之增大。

(3)其他参数不变，焊点最大径从0.40 mm增加到0.55 mm时，叠层焊点所受的最大等效应力应变增大，叠层焊点振动疲劳寿命随之减小。

[ 1 ] 黄春跃, 梁颖, 邵良滨, 等. 底充胶叠层PBGA无铅焊点随机振动应力应变分析[J]. 焊接学报,2015,36(10):33-36.

HUANG Chunyue, LIANG Ying, SHAO Liangbing, et al. Study on stress and strain distribution of PBGA stacked lead-free solder joints with underfill under random vibration load[J]. Transactions of the China Welding Institution, 2015,36(10):33-36.

[ 2 ] YAN K W, JOHNSON R W. Double bump flip-chip assembly[J]. IEEE Transactions on Electronics Packaging Manufacturing, 2006, 29(2):119-133.

[ 3 ] KESER B, YEUNG B, WHITE J, et al. Encapsulated double-bump WL-CSP: design and reliability[C]// Proceedings 51st Electronic Components and Technology Conference. [S.l.]: IEEE, 2001: 35-39.

[ 4 ] SON H Y, KIM I, LEE S B, et al. Thermal cycling reliability of Cu/SnAg double-bump flip chip assemblies for 100 μm 100 μm pitch applications[J]. Journal of Applied Physics,2009,105(1): 013522.

[ 5 ] 韦何耕,黄春跃,梁颖, 等.热循环加载条件下PBGA 叠层无铅焊点可靠性分析[J].焊接学报, 2013,34(10): 91-94.

WEI Hegeng, HUANG Chunyue, LIANG Ying, et al. Reliability analysis of plastic ball grid array double-bump lead-free solder joint under thermal cycle[J]. Transactions of the China Welding Institution,2013,34(10):91-94.

[ 6 ] ZHOU B,QIU B J. Vibration durability modeling and dynamic analysis of PBGA mixed solder joints[C]// International Conference on Electronic Packaging Technology & High Density Packaging.[S.l.]: IEEE, 2011.

[ 7 ] SHAO Liangbin, HUANG Chunyue, LI Tianming, et al. Study on impacts of configuration parameters on flip stacked Au bumps stress and strain under random vibration load[C]// 16th International Conference on Electronic Packaging Technology, ICEPT 2015[A]. 2015: 594-597.

[ 8 ] 任建峰. 基于实验数据的PCB组件模型修正和阻尼的选择[J].电子机械工程,2015,29(4):1-8.

REN Jianfeng. Model modification and damping selection of a PCB assembly[J]. Electro-Mechanical Engineering, 2015,29(4):1-8.

[ 9 ] QI H, OSTERMAN M, PECHT M. Modeling of combined temperature cycling and vibration loading on PBGA solder joints using an incremental damage superposition approach[J]. IEEE Transactions on Advanced Packaging, 2008, 31(3): 463-472.

[10] 谢定君, 王畅, 谢劲松. 电路板焊点在工程环境条件下寿命分析[J].电子质量, 2013(5): 20-24.

XIE Dingjun, WANG Chang, XIE Jinsong. Board level solder joint jife prediction under engineering environmental conditions[J]. Electronics Quality, 2013(5):20-24.

[11] UPADHYAYULA K, DASGUPTA A. An incremental damage superposition approach for reliability of electronic interconnects under combined accelerated stresses[C]// The ASME Int. Mech. Dallas: ASME, 1997.

[12] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社, 2006: 76-80.

A study on the reliability of double-bump solder joints based on Patran and frequency domain analysis under random vibration load

ZHANG Long, HUANG Chunyue, HUANG Wei, HUA Jianwei

(School of Electro-Mechanical Engineering, Guilin University of Electronic Technology, Guilin 541004, China)

Based on Patran software, the 3D finite element models of double-bump solder joints were set up. The natural frequency, vibration mode and frequency response rule of the models were analyzed under random vibration. The stress and strain distribution and the response curves of strain power spectrum density for the double-bump solder joints were obtained, and then the random vibration fatigue life of the double-bump solder joints were also calculated out based on the power spectrum and rain flow count method. The effect of the pad diameter and the maximum radial diameter for double-bump solder joints on the fatigue life of the double-bump solder joints were analyzed under random vibration. The results obtained from the simulation show that the double-bump solder joint with the height of 0.5 mm, the pad diameter of 0.3 mm and the maximum radial diameter of 0.4 mm has the fatigue life of 3 132 h under random vibration. When the pad diameter increases from 0.2 mm to 0.35 mm, the fatigue life of double-bump solder joints increases with the pad diameter. When the maximum radial diameter of solder joints increases from 0.4 mm to 0.55 mm, the fatigue life of double-bump solder joints decreases with the maximum radial diameter.

random vibration; double-bump solder joint; power spectrum; fatigue life; finite element analysis

国家自然科学基金资助项目(51465012)；广西壮族自治区自然科学基金资助项目(2015GXNSFCA139006)

2016-04-21 修改稿收到日期： 2016-06-16

张龙 男，硕士生，1989年生

黄春跃 男，博士，教授，1971年生

TG404

A

10.13465/j.cnki.jvs.2017.16.031