试验研究路基土的有效应力系数χ

(山西旅游职业学院， 山西 太原 030031)

试验研究路基土的有效应力系数χ

许雪艳

(山西旅游职业学院， 山西 太原 030031)

应用直剪试验分析了不同饱和度下，路基砂性填料的Bishop有效应力系数。试验结果验证了一般假设的局限性，标定了Alonso公式的参数。因此，该研究为更好地理解Bishop公式，以及确定非饱和土有效应力系数提供了一定的依据。

非饱和土，路基土，有效应力系数， 直剪试验，

1 .引言

Bishop (1959) 认为太沙基的有效应力理论可以推广到非饱和土中去，提出了被广泛引用的有效应力表达式：

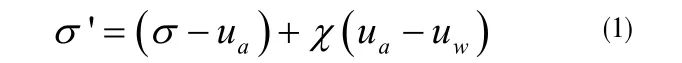
式中：σ’为有效应力；σ为总应力；ua是孔隙气压力；uw是孔隙水压力。其中引入的有效应力系数χ，其取值范围在0到1之间，当土饱和时取1，而当土完全干燥时取0。

Donald (1961) 通过控制ua和uw的三轴试验表明，有效应力系数χ是饱和度Sr的函数，即：

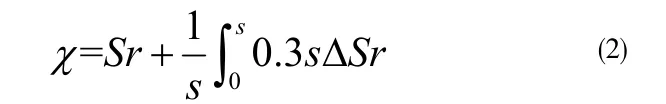
式中：Sr是土的饱和度；s是土的基质吸力。

为简单起见，众多的学者建议χ值取饱和度Sr。然而，由于χ值的复杂性，该假设往往具有局限性。例如，有实验显示，χ值不只与土的饱和度相关，也与土的吸力以及进气值相关（Khalili 和 Khabbaz, 1998），因此自然也会受到细粒含量的影响。此外，在湿陷性土浸水湿陷时, χ值甚至为负值，无法用有效应力原理来解释，当然无法与饱和度联系起来。

为明确χ值的物理意义，适用于不同类型的土材料，不同学者又提出了诸多不同形式的有效应力系数表达式：

Seker, (1983) 认为χ值是和土的相对渗透率相关的，并提出：

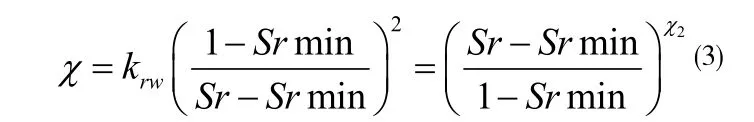
式中：krw是土的相对渗透率；Srmin是最小饱和度或残余饱和度；χ2是和土性质相关的常数。

Khalili 和 Khabbaz, (1998) 在分析多种非饱和土的基础上，提出了χ值与基质吸力间的关系表达式：

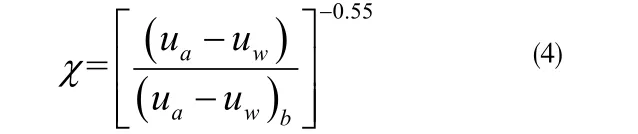
式中：(ua-uw)b是土的进气值。

近来，Alonso (2010) 等根据对粘壤土的实验，提出了更具一般性的有效应力参数表达式：

式中：α是与大孔隙占总孔隙的比值相关的参数，

当α=0，得到太沙基有效应力公式；

当α=1，得到Bishop有效应力公式的一般假设形式；

当α=∞，得到总应力公式。

对于以上的有效应力表达式，笔者认为Alonso等 (2010) 提出的形式更具普遍适用性：对于不同的土类材料，可以用抗剪强度来标定其有效应力系数的表达式。本文将利用直剪试验来测定一种非饱和砂性路基土的抗剪强度，进而确定其有效应力系数。

2 .材料及试验方法

2.1 研究材料

本文研究的材料是一种常用于公路路基填料的砂性土，取自108国道xx段。所用填料的物理性质及分类，以及击实试验按照交通部《公路土工试验规程》（JTJ051-93）进行，材料的直剪强度试验按照国家标准《土工试验规程》（GBJ123-99）执行。

该砂土的物理性质如表1所示：

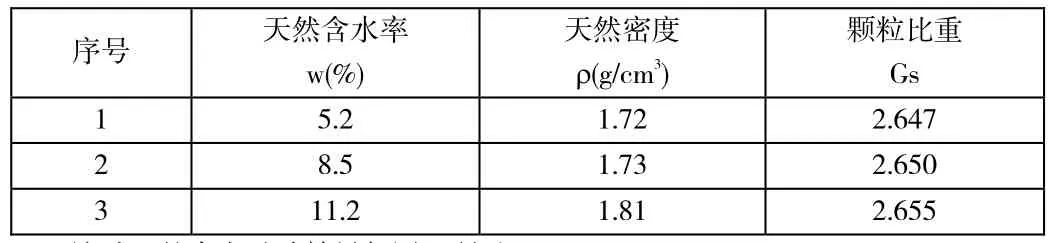
表1. 砂土的物理性质指标

该砂土的击实试验结果如图1所示：

图1. 砂土的击实曲线

根据击实曲线可知，该砂土的最大干密度为2.03g/cm3，最优含水量为8.8%。

2.2 直剪试验

测定抗剪强度的方法有直剪试验和三轴试验，方便起见，本次试验采用直接快剪的方法。试验所用的试样在不同含水量下（7.0%to 14.0%）预先压实至干密度为1.93g/cm3。其中14.0%是在该密度下的土的饱和含水率。不同含水率试样，在三个不同的竖向应力下（30kPa, 60kPaand 120kPa）确定其破坏强度，进而得到破坏线。

3 .非饱和砂土的抗剪强度

该材料的直剪试验结果如表2以及图2所示。此外，对于不同的含水率的试样，其测得基质吸力值（张力计法）也如表2所示。

试验结果表明，饱和度对于该砂土材料的抗剪强度具有十分明显地影响：随着饱和度的增加，摩擦角和粘聚力同时减小。粘聚力的明显减小可以理解为：基质吸力随着含水量增加而迅速减小，进而造成假粘聚力的损失。摩擦角的减小，则是因为含水量的增加，加强了水在土颗粒间的润滑作用。

4 .非饱和砂土的有效应力系数

基于Bishop的非饱和土有效应力假设（如式（1）），摩尔库伦准则则可以表示为：

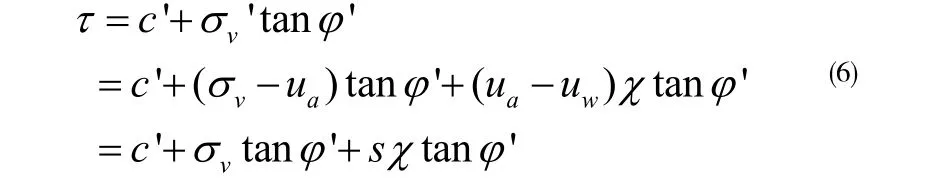
式中: τ是剪应力；φ’是饱和状态下的摩擦角；c’是饱和状态下的粘聚力。这两个值已经在表2给出（w=14.0%；φ’ =34.53°；c’=15.66 kPa）。

因此，根据式（6），有效应力系数χ可以被表述为：

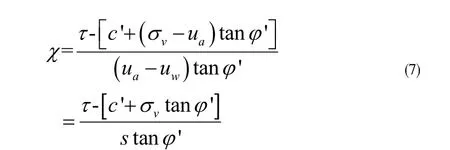
表2. 砂土的直剪试验结果

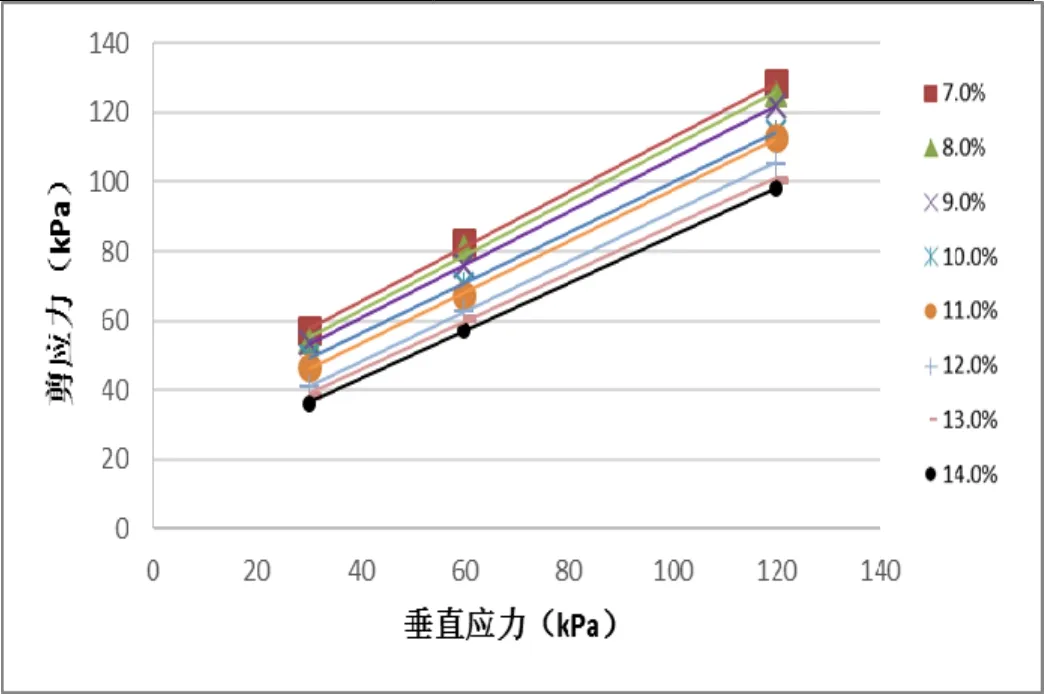
图2. 砂土不同含水率时的破坏线

进而，不同含水率下的有效应力系数可以根据式（7）计算得到，如表3所示。图3展示了本次试验的有效应力系数χ，同时也给出了χ=Srandχ=(Sr)α两个函数的曲线拟合值。由图可见，χ的试验值明显偏离χ=Sr。而χ=(Sr)α能够更好地描述该砂土在非饱和状态下的有效应力系数的分布。

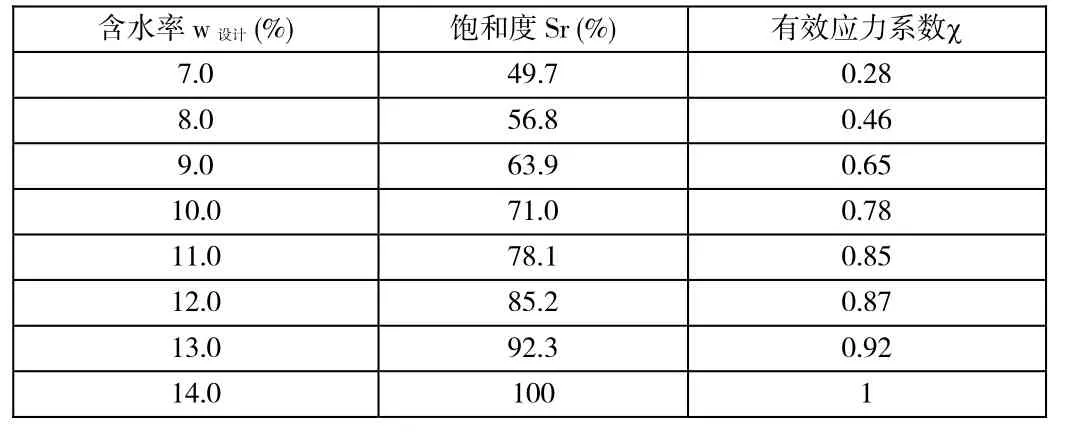
表3. 砂土在不同饱和度下的有效应力系数χ

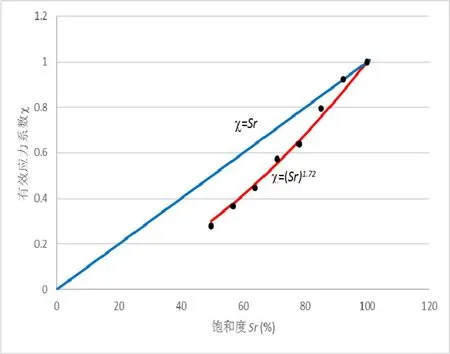
图3.砂土在不同饱和度下的有效应力系数χ

5 .结论

对于非饱和土的有效应力描述，Bishop公式长时间得到岩土工程界的认可。而其中的有效应力系数χ则直接影响着有效应力的取值。为简单起见，人们常用饱和度Sr来代替Bishop公式中的有效应力系数。然而χ值的复杂性使得该假设往往具有明显地局限性。

本文基于Alonso公式，通过研究不同饱和度下，砂土（路基填料）的直接剪切强度，进而得到随饱和度增加的有效应力系数χ的分布。结果表明χ值明显偏离一般假设（χ=Sr），而Alonso公式则能够较好的描述χ值随饱和度的分布。因此，本文建议，对于非饱和土的有效应力系数应当根据不同的材料进行实验确定。

[1] BISHOP A.W., 1959. “The principle of effective stress‟‟. Teknisk Ukeblad, 106(39), pp. 859-863

[2] DONALD I.B, 1961. “The mechanical properties of saturated and partly saturated soils with special reference to negative pore water pressure ‟‟. PhD dissertation, Univ. of London, England

[3] KHALILI N., KHABBAZ M.H., 1998. “A unique relationship for χ for the determination of the shear strength of unsaturated soils‟‟. Geotechnique, 48(2), pp. 681–687.

[4] SEKER E., 1983. “Etude de la déformation d'un massif de sol non saturé‟‟. Thèse N° 492, EPFL Lausanne.

[5] ALONSO, E.E., PEREIRA, J.M., VAUNAT, J., OLIVELLA, S., 2010. “A microstructurally based effective stress for unsaturated soils”. Géotechnique 60(12), pp. 913 –925.

[6] D.G佛雷德隆德，H.拉哈尔佐. 非饱和土土力学. 北京：中国建筑工业出版社. 1997.

U45

：B

1007-6344（2017）08-0057-02