关于半群作用的混沌及拓扑熵研究

关 鹏

(巢湖学院应用数学学院，安徽 合肥 238000)

关于半群作用的混沌及拓扑熵研究

关 鹏

(巢湖学院应用数学学院，安徽 合肥 238000)

本文归纳了半群作用的拓扑动力系统及混沌的基本概念和性质，并在Devaney混沌的基础上给出了半群作用在紧致度量空间上的混沌定义，证明了拓扑强混合蕴含Devaney混沌。同时文章还对已有的半群作用的拓扑熵概念进行了分析和总结，提出对各种不同半群作用的拓扑熵的定义之间的关系、熵值的计算和估计、正熵系统的性质以及正熵与混沌之间的关系是未来半群作用的拓扑熵研究的趋势。

半群；拓扑熵；混沌

1.引言

在拓扑动力系统的研究领域中，对于单个连续自映射是否为混沌的研究已经非常成熟，其中对于连续自映射的作用是否为混沌的判定研究的比较多，例如：是否含有Li-Yorke混沌集、是否具有对初值的敏感依赖性、是否具有正拓扑熵等都是混沌的重要判断条件。拓扑熵作为重要的拓扑共轭不变量，它的数值通常作为度量动力系统混乱、复杂程度的重要指数。自G.Cairns等人把混沌作用推广到了群作用情形以来，混沌群在国内外得到广泛的研究。D.Ellis等又进一步研究了半群作用的拓扑动力系统，取得了很多重要的研究成果，大大扩展了拓扑动力系统的研究范围。目前对于半群的混沌作用的概念和基本性质的研究比较多，但对于半群作用的混沌性的判定主要还是从“是否含有Li-Yorke混沌集、是否具有对初值的敏感依赖性”等角度研究，很少涉及到半群作用的拓扑熵的研究，而拓扑熵在判定混沌上的作用是不容忽视的。因此，本文对半群作用的混沌以及拓扑熵进行讨论，对已有的研究成果进行总结，并对未来的研究趋势进行分析。

2.半群作用的混沌动力系统

对于混沌研究的热潮开始于1975年，Li.T.Y和Yorke.J.A第一次将混沌的概念数学化，提出了Li-Yorke混沌[1]的定义，此后各种混沌定义应运而生，比较经典的有Devaney混沌[2]、Spatiotemporal混沌(简称ST混沌)[3]、混沌群[4]。对于半群的混沌作用的研究主要集中在两个方面：一是对半群混沌作用概念的研究，包括半群作用的Li-Yorke混沌[5―7]、半群作用的Devaney混沌[8]、半群作用的ST混沌[9]，以及这几种混沌定义之间的关系研究，例如半群作用的拓扑强混合蕴含Devaney混沌、Devaney混沌蕴含Li-Yorke混沌[8]等；二是对半群混沌作用的条件研究，文献[6]中借助于“Li-Yorke点对”来描述半群混沌作用，讨论了“Li-Yorke点对”的存在性，并得到半群混沌作用的充分条件。文献[10]讨论了“对初值敏感依赖性”对半群混沌作用的影响。文献[5]讨论了若和式自同态幺半群作用在Polish空间上，且含有一个拓扑传递点和周期轨道O，以至于H={s∈S:s|O是一恒等映射}，则该半群作用是混沌的。

2.1 基本概念

半群作用的拓扑动力系统的基本概念和主要性质如下。

假设X为一个集合，S为一个半群，则定义S作用在X上的一个映射 π为：π:X×S→X,即：(x,s)→xs，则有t(sx)=(ts)x, ∀t, s∈S,∀x∈X。

定义2.1[11]：称(X,S,π)为半群S作用在紧致Hausdorff空间X上的动力系统，如果在半群S作用下π是连续的。

定义2.2[11]：设半群S连续作用在拓扑空间X上，对任意的x∈X，称集合orb(x)={sx|s∈S}为x在S作用下的轨道。

定义2.3：假设(X,S,π)是一个半群作用的拓扑动力系统，则

(1)X上的非空子集A称为在半群S作用下不变，若AS={as|a∈A,s∈S}⊆A。

(2)若非空子集A是闭集且在半群S作用下不变，则限制在A×S的映射π定义了半群S在子集A上的作用，称(A,S)为(X,S)的子系统。

(5)假设A是X的非空、闭且在半群S作用下不变的子集，则A称为极小集，若(A,S)是极小的。

(6)若对X的两个任意非空开集U,V，有D(U,V)={s∈S|U∩πs-1V≠Ø}≠Ø，则称(X,S)是拓扑遍历的。

(7)若(X×X,S)是拓扑遍历的，则称(X,S)是拓扑弱混合的。

(8)若对X的两个任意非空开集U,V，存在S的紧子集K，使得SK⊆D(U,V)，则称(X,S)是拓扑强混合的。

随着对半群作用的动力系统研究的深入，很多学者开始对半群作用的混沌现象进行研究。半群作用的混沌定义大多是从区间连续自映射的动力系统或者一般拓扑动力系统的混沌定义中推广而来,如经典的Li-Yorke混沌、Devaney混沌、ST混沌等。Li.T.Y和Yorke.J.A首次在区间上的动力系统中给出了Li-Yorke混沌的定义，他们从动力系统的微观层面对混乱程度进行了数学描述。

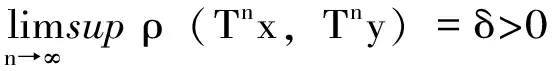
Devaney从系统的宏观层面刻画系统的紊乱程度，提出了Devaney混沌的概念。

定义2.5(Devaney混沌)[2]：设(X,ρ)是紧致度量空间，f:X→X是连续自映射，则f是Devaney混沌的，若f满足以下三个条件：

(1)f具有对初值的敏感依赖性；

(2)f在X上是拓扑传递的；

(3)f的周期点在X中稠密。

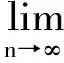
定义2.6(ST混沌)[12]：动力系统(X,T)具有对初值敏感依赖性，若任给x∈X和x的任一邻域U，都存在y∈U，使得(x,y)∈X2为Li-Yorke对。动力系统(X,T)称为是ST混沌的，若(X,T)是拓扑传递的，且对初值具有敏感依赖性。

Francois Blanchard进一步给出了拓扑弱混合、Li-Yorke混沌以及ST混沌之间的关系。

定理2.1[12]:一个动力系统(X,T)如果是拓扑弱混合的，则该系统是Li-Yorke混沌的和弱ST混沌的。

2.2 半群作用的混沌及性质

在以上经典混沌定义的基础上，很多学者将混沌定义推广到了半群作用的情形。

文献[6]在Li-Yorke混沌的基础上研究了半群作用在紧致度量空间上的Li-Yorke对的存在性。他将一般动力系统中的近邻关系概念推广到半群作用的动力系统上，给出了半群作用下存在Li-Yorke对的充分条件，同时给出了Li-Yorke混沌的充分条件。

定理2.2[6]：设交换半群S连续作用在无限紧致度量空间X上，若(X,S)是拓扑传递的且包含周期点，则(X,S)存在无限Scrambled集，即(X,S)是Li-Yorke混沌的。

文献[7]在经典的Denaney混沌的基础上，给出了半群作用的混沌定义。

定义2.7[7]：设S连续作用在紧致度量空间X上，如满足以下条件，则称该半群作用是混沌的:

(1)拓扑传递性：对X中任意两个非空开集U,V,∃s∈S使得s(U)∩V≠Ø;

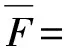
该定义可以看作是Devaney混沌在半群作用下的推广。文献[7]通过圆周上的两个连续映射，构造了作用在圆周上的半群作用，同时证明了该半群作用是混沌的。但是定义的第二个条件要求“周期点稠”过于苛刻[13]，所以笔者在此定义的基础上，给出了半群作用的混沌的另一个定义。首先给出半群作用在空间X上“对初值敏感依赖”的概念，然后通过拓扑传递性和对初值敏感依赖性定义半群作用的Devaney混沌，同时证明了半群作用的拓扑强混合蕴含了半群作用的Devaney混沌。

定义2.8：设半群S连续作用在紧致度量空间X上，如果存在δ>0，使得∀x∈X及x的任意开邻域N，∃s∈S，y∈N，使得d(sx，sy)>δ，则称S在X上的作用对初值有敏感依赖性，且敏感系数为δ。

定义2.9：设半群S连续作用在紧致度量空间X上，如果满足：

(1)拓扑传递；

(2)对初值有敏感依赖性；

则称该半群作用是Devaney混沌的。

定理2.3：半群作用的拓扑强混合蕴含了半群作用的Devaney混沌。

证:设 作用是拓扑强混合的，拓扑强混合蕴含着拓扑传递，显然S作用是拓扑传递的。下面主要证明半群S的连续作用对初值具有敏感依赖性：

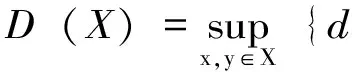
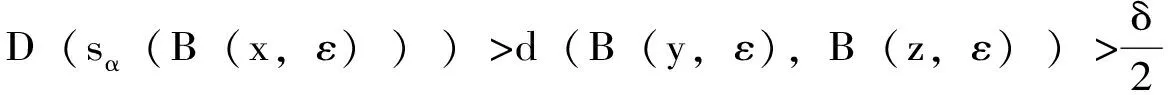
FMSchneider等利用Devaney混沌的性质，给出了半群作用混沌的另外一个概念,并给出了半群作用混沌的具体例子，φ[0,∞):[0,∞)×C([0,∞))→C([0,∞))。

定义2.10[14]：设半群S作用在拓扑空间X上，半群S的连续作用φ是混沌的，如果满足以下条件：

(1)φ是拓扑传递的;

(2)φ作用下的周期点集在X上是稠密的;

(3)φ不是极小的。

另外，FMSchneider证明了如下定理。

定理2.4[14]:任何半群S在一致Hausdorff空间X上的连续作用φ如果是混沌的，则φ必定会对初值敏感。

阎欣华等将ST混沌的相关概念推广到半群作用的动力系统中，研究了关于半群作用是Spatiotemporal混沌(ST混沌)的条件，并且讨论了拓扑强混合与ST混沌的关系。

定义2.11[9]：若(X,S)是拓扑遍历的，且∀x∈X及x的任一邻域U，∃y∈U，s.t.(x,y)是Li-Yorke点对，则称(X,S)是ST混沌的。

定理2.5[9]：设(X,S)是拓扑强混合的，若S是拓扑半群，则(X,S)是ST混沌的。

FHGhane[15]等研究了半群作用在拓扑空间上的一些随机属性，并分析了半群作用为混沌的条件。

从以上半群作用的混沌定义来看，目前关于半群作用的混沌概念主要有两种形式，一种是从系统微观结构视角，基于Li-Yorke点对寻找动力系统(X,S)的无限Scrambled集.若系统存在无限Scrambled集，则系统表现出混沌性；另一种是从系统宏观结构视角，判断系统是否具有对初值的敏感依赖性以及遍历性。

关于几种经典混沌定义之间的关系，在紧致度量空间上的连续自映射已经有了比较成熟的研究，如Devaney混沌强于Li-Yorke混沌[16]；拓扑强混合一定蕴含Devaney混沌，反之不一定成立；拓扑强混合蕴含Li-Yorke混沌，反之不一定成立[17]。但是半群作用的混沌定义之间的关系探讨目前还比较欠缺，仅知道的结论是半群作用的Devaney混沌(定义2.7、定义2.9、定义2.10)蕴含半群作用的Li-Yorke混沌、半群作用的拓扑强混合蕴含半群作用的Devaney混沌和半群作用的Li-Yorke混沌、半群作用的拓扑强混合蕴含ST混沌[9]，而半群作用的Devaney混沌和半群作用的ST混沌之间是否等价还没有确切的研究结论。

3.半群作用的拓扑熵及其性质

现有的判定半群混沌作用的条件倾向于从混沌概念和性质出发(例如：在判定半群作用是否是Li-Yorke混沌时需要研究所作用的空间是否含有Li-Yorke点对)判定半群作用的混沌性，而涉及到具体的度量空间时，这种判定方法操作起来并不容易。而拓扑熵是重要的拓扑共轭不变量，每一个紧致系统都有一个确定的拓扑熵，同时拓扑熵也是度量混沌的有效指数，所以估计和计算紧致系统的拓扑熵是拓扑动力系统研究的热点。在紧致度量空间上的一般动力系统中，正拓扑熵与混沌之间具有紧密的联系，所以半群作用下的拓扑熵研究，无论是从基本概念方法还是从熵与混沌的关系讨论方面都逐渐被学者们关注。

3.1 一般动力系统中的拓扑熵及主要结论

关于拓扑熵的研究是动力系统的一个热点，近些年来，由于拓扑熵在度量混沌程度方面的应用越来越广泛，因此也引起了许多专家学者的广泛关注。80年代，刘旺金[18]对动力系统中的拓扑熵已经取得的研究成果进行了详细的总结，对熵的Adler和Bowen定义、熵与映射的周期点数的渐近性、熵与同调的关系以及熵的连续性进行了讨论和分析，并对暂未解决的问题进行了梳理。一般拓扑动力系统中拓扑熵的基本概念如下。

设X是紧致度量空间，d是其度量，f是作用在X上的连续自映射。

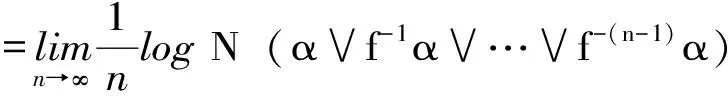
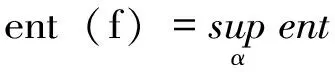
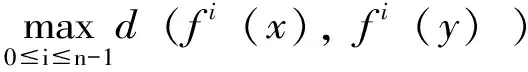
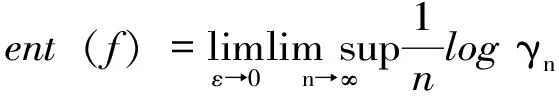
定理3.1[18]:拓扑熵的Adler定义(定义3.1)和Bowen定义(定义3.2)是等价的。

关于拓扑熵的研究主要围绕熵值的估计以及拓扑熵与混沌之间的关系展开，特别是正熵系统是否表现出混沌形态，以及0熵系统的一些性质，已有下列结论：

(1)小熵猜测

Bowen和Franks首先研究了线段上连续自映射的拓扑熵问题，提出了著名的Bowen-Franks定理：

定理3.2[21]：设f为闭区间I上的连续映射。若f有周期点的周期为n=2dm (其中m>1为奇数)(即f有非2方幂的周期点)，则f的拓扑熵大于ln2/n．

Block猜测定理3.2的逆命题也为真(即小熵猜测)，并证明了该猜测。

定理3.3[22]：闭区间I上的连续映射f的拓扑熵为0的充分必要条件为f的每个周期点的周期都是2的方幂。

事实上，以上拓扑熵在一维自映射上的性质在二维的可降映射中也是成立的，金渝光将定理3.3进行了推广。

定理3.4[23]：设f∈C0(I×I,I×I)是可降映射，则有

ent(f)=0⟸⟹PP(f)⊂{2″|n≥0} .

(2)正拓扑熵与Li-Yorke混沌

已有的拓扑熵与混沌关系的研究显示，正拓扑熵与第二节介绍的几种混沌之间虽然不是严格意义上的等价，但与混沌之间却有非常密切的联系。周作领证明了线段上连续自映射的非游荡点集上的混沌与正拓扑熵的等价性,即有

定理3.5[24]：设f∈C0(I)，则f在其非游荡点集Ω(f)上是Li-Yorke混沌的充要条件是ent(f)>0.

已有很多研究显示线段上的连续自映射存在混沌点集的本质是存在正拓扑熵，对于系统拓扑熵的计算逐渐成为研究焦点。在圆周上的单调自映射存在如下定理：

定理3.6[25]：设f:S1→S1是单调的连续映射，则f的拓扑熵h(f)=log|deg(f)|。

在线段上，针对有常斜率λ>1的连续自映射f有如下结论：

定理3.7[26]：设f∈C0(I)，且f有常斜率λ>1，则ent(f)=log(λ)，同时f有混沌点集I-Per(f)。

虽然在一些特定的系统中，正拓扑熵意味着Li-Yorke混沌，但是在一般的拓扑动力系统中，正拓扑熵与Li-Yorke并不等价，很多学者找到了反例，如文献[28]研究了线段上连续自映射拓扑熵为0的条件、文献[29]构造了拓扑熵为0的系统存在Li-Yorke混沌的条件。

定理3.8[28]：设f∈C0(I)，若f的周期点的周期存在上界，则ent(f)=0。

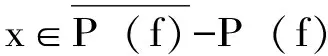
3.2 半群作用的拓扑熵及性质

随着半群作用在紧致度量空间中的研究越来越受到重视，半群作用的拓扑熵概念也被提出来，这些概念大多基于Adler和Bowen的拓扑熵定义在半群作用上的推广。

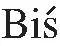
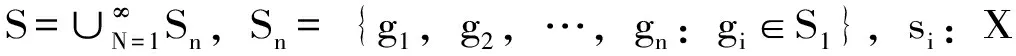
令s(n,ε,Z)为Z的(n,ε)-分离集的最大基数，γ(n,ε,Z)为Z的(n,ε)生成集的最小基数，则半群S作用在Z上的熵定义为：

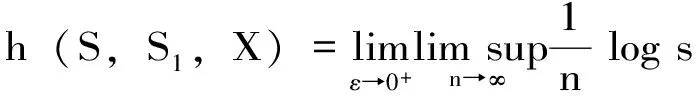
定理3.10[29]：任何由有限集S1={s1,s2,…,sk}生成的半群S，都有以下等式成立：

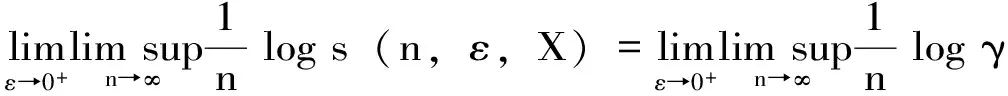
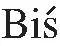
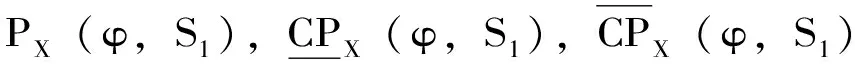
分别称为半群S作用在X上的拓扑熵、下拓扑熵和上拓扑熵。

定理3.11[30]:对任何由有限集S1={s1,s2,…,sk}生成的半群S，都有以下等式成立：

hz(S1)≥max(hz(si):si∈S1),∀Z⊂X.

定理3.12[30]:对任何由有限集S1={s1,s2,…,sk}生成的半群S，都有以下等式成立：

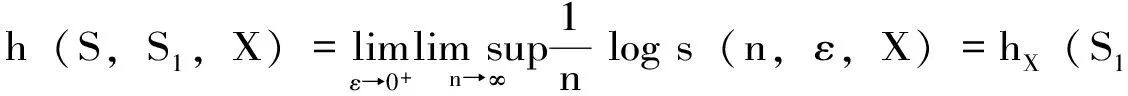
高晓燕为了研究半群作用的拓扑熵以及重分形，将Bowen拓扑熵定义推广到了半群作用在紧致度量空间上的情形，并讨论了半群作用的Bowen拓扑熵的性质。

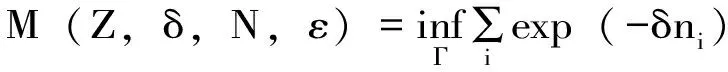
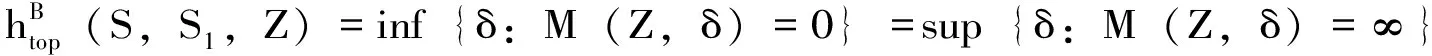
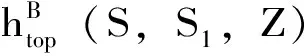
定理3.13[31]:设(X,d)是紧致度量空间，S是由有限集S1={s1,s2,…,sk}生成的半群，si:X→X是连续映射，且s1=idX。则以下结论成立：

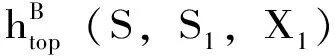
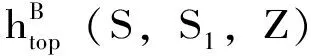
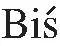
定义3.6[32]：设(X,B,m)是概率空间，fi:X→X是紧致度量空间X上的连续自映射，且fi为保测变换，i=0,1,2,…,m-1,ξ={A1,A2,…,Ak}是X上的有限可测分解，则定义分解ξ的测度熵为：

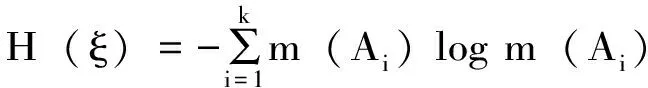
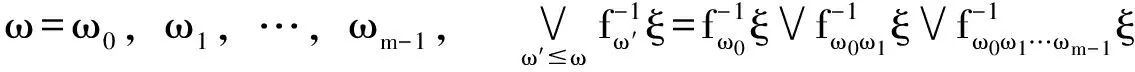
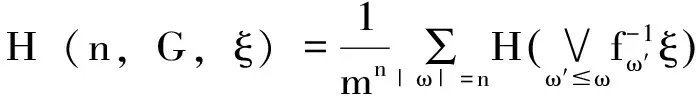
则定义自由半群G1的测度熵为：

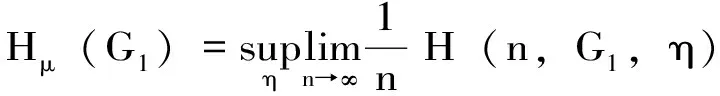
文献[32]还证明了在紧致度量空间中拓扑熵与测度熵之间有以下关系成立：

定理3.14[32]: Hμ(G1)≤h(G1)+log2,其中hμ(G1)为自由半群G1的测度熵，h(G1)为自由半群G1的拓扑熵。

同时证明了拓扑熵在等度拓扑共轭下具有不变性。

定理3.15[32]：设X,Y均为紧致度量空间，fi:K→X与gi:Y→Y是等度拓扑共轭的，i=0,1,2,…,m-1，G1={f0,f1,…,fm-1},G2=(g0,g1,…,gm-1)，则有

h(G1)=h(G2) .

从以上研究结果来看，目前关于半群作用的拓扑熵的研究还处于概念和性质研究阶段。半群作用的拓扑熵概念还不统一，目前存在的定义至少有Adler拓扑熵、Bowen拓扑熵、测度熵等，这些拓扑熵之间存在怎样的关系还需要进一步的研究和讨论。目前关于半群作用的拓扑熵值的计算还比较少，仅停留在概念层面，对熵值的估计(上界、下界)等还需要进一步的研究。另外，半群作用的拓扑熵与半群作用的Devaney混沌、Li-Yorke混沌以及ST混沌之间的关系还缺少系统性的研究，如半群作用的正熵是否与半群作用的混沌等价、是否存在0熵的混沌系统等等。

[1]LiT．Y．andYorke.．J．A．Periodthreeimplieschaos[J]．Amer．Math．Monthly，1975，(82)：985―992．

[2]DevanneyR．AnIntroductiontoChaoticDynamicalSystems[M].ReadingMA：AddisonWesley，1989．

[3]BlanchardF,GlasnerE,KolyadaS,etal.OnLi-Yorkepairs[J].JournalFürDieReineUndAngewandteMathematik, 2002, 547(547):51―68.

[4]CairnsG，DavisG，EltonD，etal．ChaoticGroupActions[J]．Enseign．Math．1995，41：123―133．

[5]HuoyunWang,XiongwuLong,HemanFu．Sensitivityandchaosofsemigroupactions[J].SemigroupForum，2012，84:81―90.

[6] 苏郇立. 半群作用Li-Yorke对的存在性[J]．纯粹数学与应用数学，2010，26(4)：608―613.

[7] 苏郇立，周友成．半群的混沌作用[J]．高校应用数学学报A辑，2004，19(3)：292―296.

[8] 关鹏, 张荣. 半群作用的Devaney混沌[J]. 江西师范大学学报:自然科学版, 2008, 32(1):32―35.

[9] 阎欣华, 任蕴丽. 关于半群作用是spatiotemporal混沌的几点注记[J]. 北京石油化工学院学报, 2011, 19(1):58―60.

[10]PengGuan,YunQian.SensitiveDependenceonInitialofChaoticsemi-groupactions[J]. 2012 8thInternationalConferenceonNaturalComputation, 2012, 3:957-959.

[11]EllisDB,NerurkarM.Thetopologicaldynamicsofsemigroupactions[J].CriticalReviewsinOncology/hematology, 2001, 60(4):268.

[12]BlanchardF,GlasnerE,KolyadaS,etal.OnLi-Yorkepairs[J].JournalFürDieReineUndAngewandteMathematik, 2002, 547:51-68.

[13] 周作领．一维动力系统[J]．数学季刊，1988，3(1)：1―23.

[14]SchneiderFM,KerkhoffS,BehrischM,etal.Chaoticactionsoftopologicalsemigroups[J].SemigroupForum, 2013, 87(3):590―598.

[15]GhaneFH,SarizadehA.Somestochasticpropertiesoftopologicaldynamicsofsemigroupactions[J].Topology&ItsApplications, 2016, 204:112―120.

[16]WenH,YeX.Devaney'schaosor2-scatteringimpliesLi-Yorke'schaos[J].Topology&ItsApplications, 2002, 117(3):259―272.

[17] 范钦杰. 混沌与拓扑强混合[J]. 大学数学, 2004, 20(6):68―72.

[18] 刘旺金. 动力系统中拓扑熵的研究[J]. 数学进展, 1982, 11(2):89―100.

[19]AdlerRL,McandrewMH.Topologicalentropy[J].TransactionsoftheAmericanMathematicalSociety, 1965, 114(2):309―319.

[20]BowenR.Entropyforgroupendomorphismsandhomogeneousspaces[J].TransactionsoftheAmericanMathematicalSociety, 1971, 153:401―401.

[21]BowenR,FranksJ.Theperiodicpointsofmapsofthediskandtheinterval[J].Topology, 1976, 15(4):337―342.

[22]BlockL.HomoclinicPointsofMappingsoftheInterval[J].ProceedingsoftheAmericanMathematicalSociety, 1978, 72(3):576―576.

[23] 金渝光. 关于一类自映射的拓扑熵[J]. 重庆师范大学学报(自然科学版), 1995(1):22―25.

[24] 周作领. 符号动力系统[M]. 上海科技教育出版社, 1997.

[25] 何连法, 王在洪. 圆周上单调映射的拓扑熵[J].JournalofMathematicalResearchwithApplications, 1996(3):379―382.

[26] 陈建威. 线段自映射f∈C～0(I)的周期点与拓扑熵[J]. 云南师范大学学报(自然科学版), 2001, 21(3):11―16.

[27] 周作领, 刘旺金. 线段自映射拓扑熵为零的一个充分条件[J]. 数学进展, 1982, 11(3):216―219.

[28]YangJ.SufficientConditionsofaChaoticMapwithTopologicalEntropy0[J].JournalofMathematicalResearch&Exposition, 1990, 10(1)：56―58.

[30]Ma,Dongkui,Wu,etal.Topologicalpressureandtopologicalentropyofasemigroupofmaps[J].Discrete&ContinuousDynamicalSystems, 2011, 31(2):545―557.

[31] 高晓燕. 半群作用的拓扑熵及其重分形分析[D]. 南京:南京师范大学硕士学位论文, 2014.

[32] 薛丽翠. 自由半群作用的熵及原像熵[D]. 石家庄：河北师范大学硕士学位论文, 2012.

(责任编辑 李艳梅)

AStudyonChaosandTopologicalEntropyBasedonSemigroupAction

GUANPeng

(Department of Applied Mathematics, Chaohu University, Hefei, 238000, Anhui Province)

Inthispaperthebasicconceptsandpropertiesoftopologicaldynamicalsystemandchaosarediscussed,thenbasedontheDevaneyChaosadefinitionofchaosinthecompactmetricspaceofsemigroupactionispresented,whichprovedthetopologicalstrongmixingcontainingDevaneychaos.Then,thepaperanalyzesandsummarizesthedefinitionoftopologicalentropybasedontheexistedsemigroupaction.Furthermore,thethesisproposesthatthefutureresearchwillbefocusedontherelationshipbetweendifferentdefinitionsoftopologicalentropy,calculationandestimationofentropyvalue,propertiesofpositiveentropysystem,andtherelationshipbetweenpositiveentropyandchaos.

semigroup;topologicalentropy;chaos

安徽省教育厅自然科学研究项目“基于半群作用的Li-Yorke混沌和拓扑熵之间关系的研究”，项目编号：KJ2013B165。

2017 - 03 - 14

关 鹏(1983―)，男，巢湖学院应用数学学院讲师，硕士研究生，研究方向：拓扑动力系统。

O

A

1671 - 7406(2017)03 - 0005 - 08