一种新颖的LTE-A上行频域资源调度算法
崔建明, 王昕, 巢志俊
(1. 复旦大学 信息科学与工程学院, 上海 200433; 2. 上海华为技术有限公司, 上海 200135)
一种新颖的LTE-A上行频域资源调度算法
崔建明1, 王昕1, 巢志俊2
(1. 复旦大学 信息科学与工程学院, 上海 200433; 2. 上海华为技术有限公司, 上海 200135)
LTE-A上行多址接入技术采用的clustered DFT-s-OFDMA方式允许用户获得频域资源上最多两段不连续的资源块(Resource Block, RB);该项技术增加了资源分配的灵活性,同时也增加了资源分配的难度。特别是,在前述松弛的连续性限制条件下,上行资源调度还需要进一步考虑LTE-A协议对RB分配附加的其它约束,包括离散傅里叶变换(Discrete Fourier Transform, DFT)实现带来的质因数分解限制和下行控制信息(Downlink Control Information, DCI)格式限制带来的RBG(RB Group)粒度限制。针对这些难点,设计了一种基于两轮分配的新颖的LTE-A上行资源调度算法——选址扩张算法。该算法有极低的计算时间复杂度,同时在性能和最优算法给出的上界差距很小,比其他一些现有的典型调度算法在性能和/或计算时间复杂度上有明显的优势,很适用于实际LTE-A系统。
LTE-A; 上行; 资源分配; NP-hard; 次优算法; 低复杂度
0 引言
随着移动互联的发展,人们对移动数据的需求越来越大。根据现有的统计,自2012年以来,全球的移动数据流量的年复合增长率达到了66%;而预计在2017年,全球每个月的移动数据流量将会超过10×260字节[1]。为了满足用户对移动数据的需求,3GPP也在积极推进现有移动互联网的演进。目前,LTE网络已经全面商用,并且正向LTE-A网络演进。作为LTE的演进网络,LTE-A起到了承前启后的作为,同时也在逐步商用,帮助全球度过LTE到5G的过渡阶段。为了提高网络吞吐能力,多点协作、载波聚合等技术在LTE-A中被运用。在上行多址接入技术方面,更灵活的clustered DFT-s-OFDMA取代了LTE的集中映射式的DFT-s-OFDMA,打破了用户只能获取频域上一段连续资源块(RB)的限制,允许用户在上行资源分配过程中可以获得多段不连续的RB,增加了调度灵活性;而好的上行资源调度算法可以充分发挥出新的多址接入技术带来的增益。
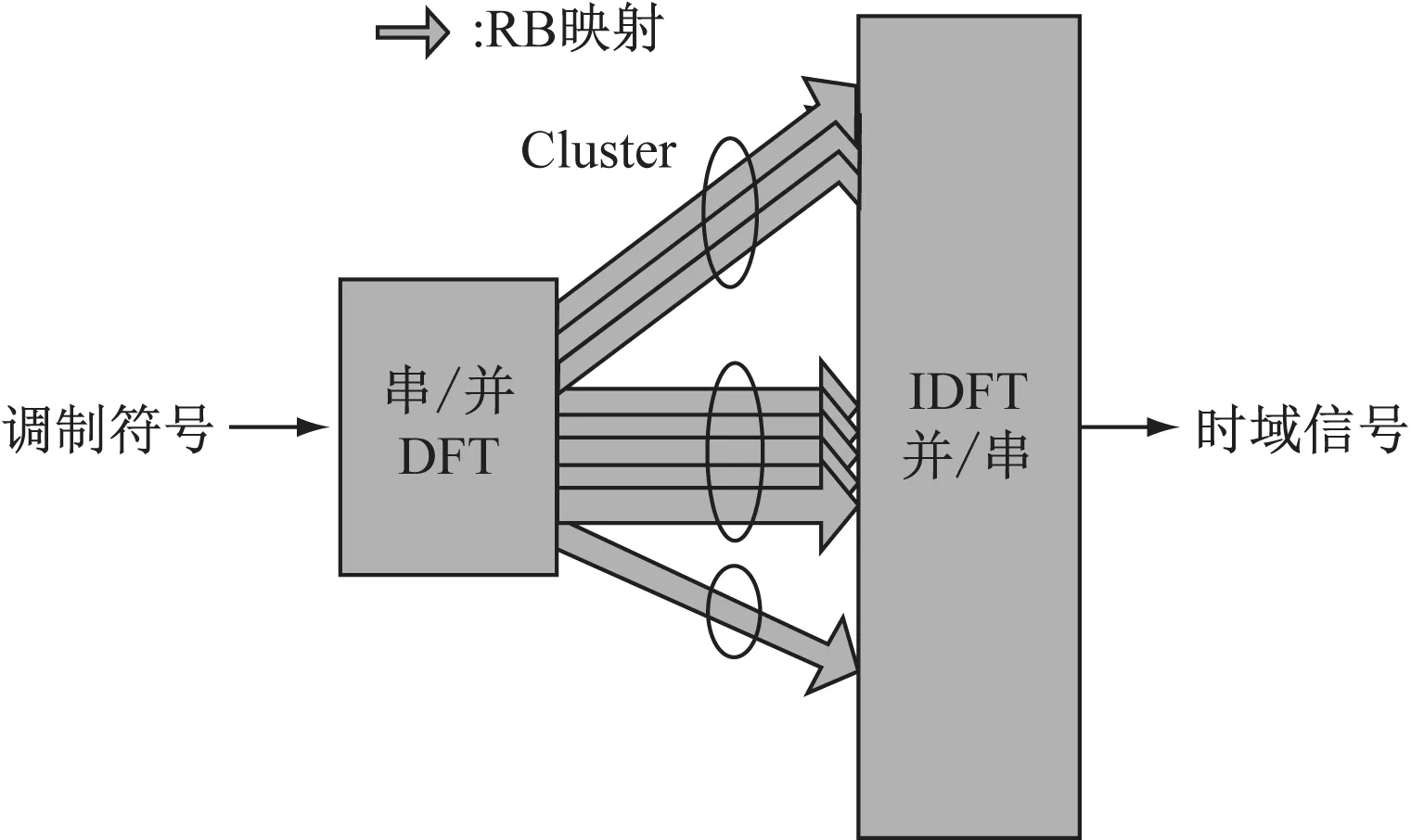
图1 Clustered DFT-s-OFMA的RB映射关系图
在实际的LTE-A上行链路中,为了减少传输控制信息所需的比特数从而与LTE中的下行控制信息(Downlink Control Information, DCI)格式兼容,协议规定在每个TTI(Transmit Time Interval)内,每个用户最多可以获得两段不连续的频域资源,且当一个用户获得两段不连续的频域资源时,每一段频域资源必须以RBG(RB Group)为粒度[2](RBG由频域上若干个RB组成);而当用户仅获得一段连续的频域资源时,其分配粒度是RB(按协议规定一个RB包含12个连续子载波,持续时间长度为1ms[3];因为本文聚焦在子载波资源分配,所以忽略RB在时间上的定义)。同时考虑到离散傅里叶变换(Discrete Fourier Transform, DFT)应用的复杂度问题,DFT变换矩阵大小须以2,3,5作为基数[4],所以协议规定每个用户获得的RB数目必须满足NRB=2a·3b·5c,其中a,b,c为非负整数[4]。
作为LTE-A上行资源调度的子问题,LTE上行资源调度问题被广泛研究:文献[5]提出利用分支定界算法获得LTE上行资源分配问题的最优解,但是最优算法计算复杂度极高。文献[6]-[7]针对相邻限制条件约束的LTE上行资源调度问题,提出了3种近似算法。文献[8]证明了在仅考虑相邻限制条件下,LTE上行链路分配问题为NP-hard问题,同时给出了4个次优的贪婪算法。对于LTE-A上行资源调度问题也有少量研究:文献[9]中作者根据文献[6]的收益倍增思想,提出了适用于LTE-A上行资源调度问题的收益倍增算法。文献[10]中作者利用拉格朗日对偶法对LTE-A上行资源调度问题进行求解,然而该算法复杂度较高,且对效益函数的凸性有严格要求。事实上,上述工作均没有考虑协议对于上行资源调度问题的具体约束。为此,本文考虑了上述所有限制条件,提出了一种基于两轮分配的新颖的调度算法——选址扩张算法,通过先进行粗颗粒分配再进行细颗粒分配的方式,为算法提供了对抗信道突变的鲁棒性,同时保证了调度的灵活性,保证了良好的仿真性能。此外,本文提出的选址扩张算法还具有极低的计算时间复杂度,很适用于实际系统。
2 系统模型
考虑采用clustered DFT-s-OFMDA的LTE-A非协作多小区上行网络,假设每个小区内共有K个单天线用户,标识为集合Ψ={1,…,k,…,K},传输带宽B被正交地划分为M个RB,标识为集合Ω={1,…,m,…,M}。假设基站端采用MMSE接收机且配有两根天线,基站n中用户k在子载波j上的信干噪比SINR可以表示为式(1)。
(1)
其中R(RB(j))表示子载波j所在RB上的各个子载波平均干扰协方差矩阵,hk,j,n表示信道增益,pk,j,n表示用户k在子载波j上的发送功率。根据协议规定[11],用户采用平均分配策略进行功率分配pk,j=pk,i,∀i,j,总发送功率Pk采用开环控制,由式(2)决定,
Pk=min{Pmax-MPR,P0+αPL+10log10Nk}
(2)
其中Pmax表示最大发送功率,PL表示传播路径损耗,P0表示开环发射功率,α表示路径损耗补偿系数,Nk表示用户k所获得的RB数。MPR (Maximum Power Reduction)表示最大功率回退,其设计初衷是为了抑制多个cluster(不连续的RB)传输产生的交调乘积(Inter-Modulation Products, IMP)。协议规定[11],对于多个cluster在单个CC (Component Carrier)同时传输的情况,最大输出功率允许的MPR表示如式(3)。
MPR=CEIL{MA,0.5}
(3)
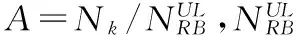
根据MMSE接收机的性质,用户k在调度带宽上整体的SINR可以表示为式(4)[12]。
(4)
Mk代表用户k获得的子载波数。
3 LTE-A上行资源调度问题
我们假定基站已知本小区用户所有信道状态信息(Channel State Information, CSI)。定义分配给用户k的RB集合为ak,则用户k的容量可以表示为式(5)。
(5)

s.t.
(6)
式(6)中的第一个限制条件表示排他性限制,即每个RB最多只能被一个用户占用;而A表示所有可行方案ak的集合。针对LTE-A上行链路,考虑LTE-A协议对于上行资源调度的约束,ak需要满足以下限制条件:
1) 松弛的相邻性限制:ak最多包含两段不连续的RB,每段中的所有RB必须是相邻的;
2) 质因数分解限制:ak所包含的RB数的质因数分解必须是{2,3,5}的子集,即Nak=2a·3b·5c,Nak表示ak所含RB数,a,b,c为非负整数;
3) RBG粒度限制:对于包含两段不连续RB的ak,其每段RB必须以RBG为粒度。假设RBG大小为P,则第i个RBG所包含的RB编号为(i-1)P+1~min(iP,M)。
原有LTE上行资源调度问题和式(6)相比,限制条件有所变化:没有限制条件3),同时限制条件1)变成仅允许包含一段连续的RB,因此其可看成是式(6)的子问题。LTE上行资源调度问题已经被证明是NP-hard问题[8],因此式(6)同样也是NP-hard问题,无法在多项式时间内计算得到该问题的最优解。对此,本文提出了一种新颖的基于两轮分配的选址扩张算法;该算法能以极低的计算时间复杂度获得近似最优的LTE-A上行资源调度方案。
选址扩张算法分为3个阶段:选址、扩张和调整。在选址阶段,算法利用粗颗粒的chunk(若干个连续RB)作为最小调度单位,可以充分利用信道的相关性,提高算法对抗信道突变的鲁棒性,在扩张阶段,算法在选址阶段的基础上利用小颗粒的RB作为调度单元,从而保证调度的灵活性。由于式(6)中的限制条件2)和3)使得该问题很难解决,所以在前两个阶段暂时不考虑这两个限制条件。在完成这两个阶段后,通过调整阶段使得最后分配结果满足限制条件2)和3)。以下是算法的具体步骤:
步骤1:初始化阶段:基站获得所有用户最新的信道状态和其余小区4个TTI前的分配结果(对于多小区的非协作调度,基站利用其他小区4个TTI前的分配结果作为干扰进行考虑),同时调用前期资源分配得到的用户平均传输速率R={R1,…,Rk,…,RK}用来后续计算加权速率。
步骤2:选址(Nesting)阶段:基站按照RBG大小将所有RB划分为资源大块chunk,作为该阶段分配的最小单元。基站每次从所有可行的chunk-用户对中选取加权速率增益最大的chunk-用户对进行分配,同时更新该用户在其余备选chunk的加权速率增益以及各个用户的可行chunk集。重复分配过程直至没有可行的chunk或最大加权速率增益小于等于0。具体为:
假设RBG大小P,第i个chunk(记为Ci)包含编号为i到min(i+P,M)的RB。与RBG不同,相邻若干个chunk之间会有重叠。计算所有用户在各个chunk上的加权速率w,并存储在O(M)×K矩阵Vc内。
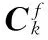
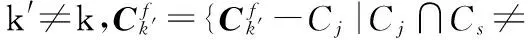
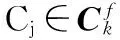
更新各个用户在各自备选chunk上的加权速率增益为式(7)。
(7)
对于非备选chunk上的加权速率增益,置0,即为式(8)。
(8)
步骤3:扩张(Expanding)阶段:该阶段分配以RB为粒度进行。基站根据Ωk更新各个用户的备选RB,每次从所有备选的RB-用户对中选取加权速率增益最大的RB-用户对进行分配,同时更新该用户的备选RB集合以及在备选RB上的加权速率增益。重复步骤3的分配过程直至没有可行的RB或总加权速率不再增加。
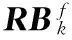
(9)
在非备选的RB上,用户加权速率增益置0:为式(10)。
(10)
步骤4:调整阶段:由于前两个阶段没有考虑质因数分解限制和RBG粒度限制,所以该阶段需要对Ωk, ∀k进行调整,以保证所有Ωk均符合限制条件1)~3)以及排他性限制条件。基站采用一种贪婪的调整策略进行调整,调整策略如下:
基站根据Ωk为所有用户进行优先级排序,2-cluster(包含两段不连续RB)的Ωk优先级高于1-cluster(只包含一段连续RB)的优先级;而针对拥有相同cluster数的Ωk,RB数量多的优先级高于RB数量少的优先级。调整次序按照优先级大小来进行,某个用户调整一旦完成,其分配结果就被固定,即优先级小的用户调整过程中不能改变优先级高的用户方案。调整过程当中,尽可能的保证RB的变动最小化,以达到最小化性能损失的目的。
最小化RB变化数通过以下方式实现,对于2-cluster的方案,由于RBG的位置是固定的,所以可以通过方案中每段的最大和最小的RB编号来确定应该调整的位置。而对于1-cluster的方案,可以通过该方案所包含的RB数和与该RB数相差最小可行方案RB数比较,来确定可行的调整方向和策略(向左添加RB或者向右添加RB或者左端删除RB或者右端删除RB)。如果存在多种可选的情况,则对比多种调整情况带来的性能损失,挑选性能损失最小的作为最终调整方式。例如Ωk有7个RB,则可以通过共4种方案将其扩成8个RB或者缩减成6个RB,以满足质因数分解限制,最终方案的确定只需要比较这4种方案带来的性能损失即可。由于用户的方案调整可能会对其相邻用户方案产生影响,所以每完成一个用户方案的调整,需要更新剩余未调整用户的分配结果。
总体算法如下表所示:
算法:选址扩张算法
1: Initialize: 初始化用户集Ψ{1,…,k,…,K},RB集Ω{1,…,m,…,M}和RBG 大小P; 获取各用户的长期平均速率R={R1,…,Rk,…,RK}和CSI;初始化各用户所获得的RB集Ωk=Ø,∀k;
2: Nesting: 初始化总的chunk集C{Ci|1≤i≤M-P+1},其中Ci={RBi,…,RBmin{i+P,M}}; 初始化各用户备选chunk集,∀k并计算chunk-用户对加权速率矩阵Vc;
3: Repeat:
4:ws,k=max{Vc};
5: ifws,k<0
6: break;
7:Ωk=Ωk+Cs;
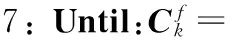
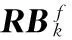
9: Repeat:
10:Δs,k=max{VRB};
11: ifΔs,k<0
12: break;
13:Ωk=Ωk+RBs;

16: 设置调整优先级并调整Ωk;
17:Output:{Ωk,∀k}
算法复杂度分析:选址扩张算法的总体计算时间复杂度为O(M(K+M))。由于算法的复杂度主要来源于对加权速率的计算,因此本文利用对加权速率计算的次数来衡量计算时间复杂度。选址阶段的计算时间复杂度是O(M(K+M)):计算chunk-用户对加权速率矩阵Vc计算时间复杂度是O(MK)。在分配chunk的过程中,根据(7)每次最多需要更新其中一行的加权速率值,每次更新的复杂度为O(M),循环次数为O(M),所以选址阶段的计算时间复杂度为O(MK)+O(M2)=O(M(M+K))。扩张阶段的计算时间复杂度是O(MK):在最坏情况下(大多数用户在第一轮没有获得RB)计算加权速率矩阵VRB的计算时间复杂度为O(MK)。而在循环过程中,由于该阶段只能在相邻的RB附近进行扩张,所以每次只需要更新O(1)的加权速率值,循环持续O(K),所以扩张阶段计算时间复杂度为O(MK)。调整阶段的计算时间复杂度为O(MK):对于未调整的Ωk,只有存在多个备选替换方案时才需要计算加权速率。对于2-cluster的Ωk,由于RBG位置固定的特性,备选方案可以通过Ωk中的2个cluster位置唯一确定。对于1-cluster的Ωk,由于只需要通过简单的调整使得把Ωk内的RB数往其最相邻的符合质因数限制的数字上靠,备选方案不会超过O(M),所以该阶段在最坏情况下需要O(MK)的计算时间复杂度。因此算法整体的计算时间复杂度为O(M(K+M))。
4 仿真结果
仿真环境描述如下:LTE-A上行带宽设置为10 MHz,RB数目为50个,载波频率2 GHz。小区拓扑包含17个3扇区站点,站点间距500米。每个扇区活跃用户数为6人,用户均匀分布,且移动速度为3 km/h。小区路径损耗补偿系数和开环发射功率设置为[α,P0]=[0.8,-95 dBm],大尺度路径损耗模型为PL=128.1+37.6×log10(x),x单位为km;阴影衰落服从对数正态分布,标准差为8 dB;信号穿透损耗20 dB。同时,我们假定噪声功率谱密度为-174 dBm/Hz,仿真采用20径典型城市信道模型。
本节从用户速率的经验分布函数(empirical CDF)、小区吞吐量和归一化的CPU时间等方面,将选址扩张算法和LTE-A下的基于分支定界思想的最优算法、局部比(Local Ratio)算法、收益倍增(Double Benefit)算法和经典的轮叫(Round Robin)算法进行比较。值得一提的是,由于算法特性,LTE中的最优算法、局部比算法和收益倍增算法可以直接应用于在协议约束下的LTE-A上行资源调度问题,其计算时间复杂度,如表1所示。

表1 算法数据比较
从CDF曲线可以看出,如图2所示。
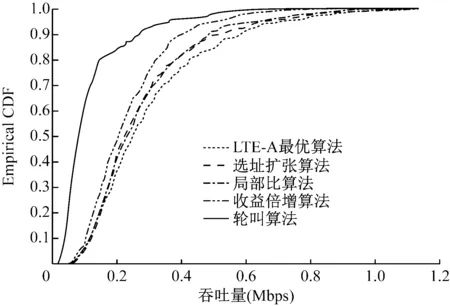
图2 用户速率的经验CDF曲线
选址扩张算法和最优算法相比性能差距很小,从表1可以发现,二者的小区平均吞吐量性能仅相差大约8%。而从算法的计算时间复杂度和归一化CPU时间来看,选址扩张算法要远优于最优算法(例如,前者所需CPU时间仅为后者的0.6%)。同时,和近似比为3的局部比算法相比,选址扩张算法的性能略优于局部比算法,而CPU时间和计算复杂度上要8倍低于局部比算法。同收益倍增算法相比,本文提出的算法在系统性能和计算复杂度上均要优于收益倍增算法,性能增益约为20%,且所需CPU时间节省约7倍。同轮叫算法相比,虽然所提出的算法计算时间复杂度大于轮叫算法,但是选址扩张算法在系统性能上要远远优于轮叫算法,小区吞吐量增益超过130%。所以本文提出的选址扩张算法在仿真性能和计算复杂度上均有很优秀的表现,考虑到其仅有平方量级的计算复杂度以及和最优算法之间极小的性能差距,选址扩张算法很适用于实际LTE-A系统。
5 总结
在考虑LTE-A协议约束的情况下,本文设计了一种基于两轮分配的新颖的LTE-A上行资源调度算法——选址扩张算法。该算法只有平方量级的计算时间复杂度,远小于最优算法,同时在算法性能和最优算法给出的上界差距很小,比其他一些现有的典型调度算法在性能和/或计算时间复杂度上有明显的优势,很适用于实际LTE-A系统。
[1] Index CVN. Cisco visual networking index: global mobile data traffic forecast update, 2014-2019[R]. Tech. Rep., 2015.
[2] 3rd Generation Partnership Project (3GPP) Technical Specification Group Radio Access network; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical layer procedures(Release 11)[S]. 3GPP TS 36.213, V11.11.0, Jun. 2015.
[3] 3rd Generation Partnership Project (3GPP) Technical Specification Group Radio Access network; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical channels and modulation (Release 11)[S]. 3GPP TS 36.211, V11.6.0, Sept. 2014.
[4] Ericsson. DFT size for uplink transmissions[C]. 3GPP TSG RAN WG1 Meeting 46, Seoul, R1-062859, 2006,10.
[5] Wong I C, Oteri O, Mccoy W. Optimal resource allocation in uplink SC-FDMA systems[J]. IEEE Transactions on Wireless Communications, 2009, 8(5):2161-2165.
[6] Ren F, Xu Y, Yang H, et al. Frequency Domain Packet Scheduling with Stability Analysis for 3GPP LTE Uplink[J]. IEEE Transactions on Mobile Computing, 2013, 12(12):2412 - 2426.
[7] Andrews M, Zhang L. Multiserver scheduling with contiguity constraints[C].INFOCOM 2009, IEEE. IEEE, 2009: 1278-1286.
[8] Lee S, Pefkianakis I, Meyerson A, et al. Proportional Fair Frequency-Domain Packet Scheduling for 3GPP LTE Uplink[C].INFOCOM 2009, IEEE. IEEE, 2009:2611-2615.
[9] Prasad N, Zhang H, Jiang M, et al. Resource Allocation in 4G MIMO Cellular Uplink[C].Global Telecommunications Conference (GLOBECOM 2011), 2011 IEEE. IEEE, 2011:1-5.
[10] Balasubramanya N M, Lampe L. Near-optimal resource block and power allocation mechanisms in uplink for LTE and LTE-Advanced[C].GLOBECOM Workshops. IEEE, 2014:1014-1019.
[11] 3rd Generation Partnership Project (3GPP) Technical Specification Group Radio Access network; Evolved Universal Terrestrial Radio Access (E-UTRA); User Equipment (UE) radio transmission and reception (Release 10)[S], 3GPP TS 36.101, V10.21.0., Jan. 2016.
[12] Assaad M, Ben-Ameur W, Hamid F. Resource optimization of non-additive utility functions in localized SC-FDMA systems[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4896-4910.
A Novel Resource Allocation Algorithm for the LTE-A Uplink
Cui Jianming1, Wang Xin1, Chao Zhijun2
(1. Department of Communication Science and Engineering, Fudan university, Shanghai 200433, China;2. Shanghai Huawei Technology Co., Ltd. Shanghai 200135, China)
In this paper, we address the resource allocation problem for the clustered DFT-s-OFDM A based LTE-A uplink,where each user can be allocated up to two nonconsecutive clusters of resource blocks (RBs). To accommodate the flexibility brought by the clustered DFT-s-OFDM, LTE-A standard imposes additional constraints on the RB allocation, such as the discrete-Fourier-transform implementation constraint, andmultiple granularity constraint. These considerations make the relevant resource allocation problem very difficult to be tackled. To this end, an efficient resource allocation algorithm called “nesting and expanding” is proposed. Simulation results show that the proposed low-complexity algorithm can achieve a near-optimal performance, and significantly outperform the existing alternatives.
LTE-auplink; Resource allocation; NP-hard; Suboptimal algorithm; Low-complexity
崔建明(1991-),硕士研究生,研究方向:无线通信。 王 昕(1971-),教授,研究方向:无线通信,信号处理。 巢志俊(1973-),工程师,研究方向:无线通信。
1007-757X(2017)08-0057-04
TP311
A
2017.04.12)

