铅芯橡胶隔震支座大变形硬化模型及隔震结构弹塑性分析研究
吴倩芸, 何文福, 刘文光, 于维欣, 秦 川
(上海大学 土木工程系,上海 200072)
铅芯橡胶隔震支座大变形硬化模型及隔震结构弹塑性分析研究
吴倩芸, 何文福, 刘文光, 于维欣, 秦 川
(上海大学 土木工程系,上海 200072)
对直径为600 mm和1100 mm的铅芯橡胶支座进行了剪切变形400%的水平大变形剪切试验,试验结果表明支座在240%剪切变形后发生屈服后刚度增大现象,且硬化刚度随剪切变形的增大而增大,400%剪切变形时刚度硬化增加到1.5倍。根据试验结果进一步提出了一种考虑硬化效应的铅芯橡胶支座多线性大变形硬化恢复力模型,并将此模型用于Perform-3D软件中。对8层隔震结构进行不同地震烈度下的弹塑性分析,支座分别采用传统双线性模型与多线性大变形硬化模型,对比分析结构的地震动响应、弹塑性反应谱以及塑性耗能情况。结果表明在大震下隔震支座硬化隔震效果减弱,上部结构加速度增加30%~50%,结构塑形耗能增加,上部结构进入塑性变形状态。研究结果表明隔震设计中大震验算不考虑支座硬化效应会低估结构地震反应。
支座硬化;地震动响应;反应谱;能量
美国Northridge地震、日本阪神地震及我国汶川地震的强震中采用隔震技术的建筑物和桥梁具有良好抗震性能的表现,极大地推动了这一技术的进一步应用,同时国际上也由此兴起了一股隔震应用热潮。因此,对于不同于传统抗震理念的基础隔震结构领域的研究有着重大意义。新抗规[1](GB-50011—2010)中引入了建筑抗震性能化设计的理念,使结构在未来的地震灾害下能够维持所要求的性能水平,而不仅仅是大震不倒,从而避免结构在中小地震灾害下丧失正常使用功能导致巨大的经济损失。传统抗震结构基于弹塑性分析的性能化抗震设计已在国内外开展研究并取得众多成果,1995 年,美国的加州工程师协会(SEAOC)在采用新地震动参数区划图和吸取 Northridge、 Kobe 等震害教训的基础上,提出来基于性能化设计的概念[2]。1996 年,美国 ATC颁布了专门用于混凝土结构抗震性能评估和修复的文件(ATC-4),对结构性能评估采用能力谱法来确定目标位移[3]。随后的1997 年,美国 FEMA颁布了 FEMA 273和 FEMA 274,两个文件分别对延性构件和非延性构件在性能评估上给出了详细的可接受准则参数[4-5]。2006 年,在 FEMA356 基础上ASCE颁布了正式的法规性规范 ASCE41[6]。2010 年,美国太平洋地震工程研究中心于 11 月颁布了高层抗震设计导则作为太平洋地震工程研究中心的高层建筑推进计划的主导成果,目前已在若干工程中参考使用[7]。由此,美国开始步入基于性能的高层建筑抗震设计阶段。国内建筑的性能化设计最早运用在超限建筑中。目前国内的超高层建筑越来越多,经过多年的工程经验积累和国内外研究界的进展,在 2011 年新执行的《建筑抗震设计规范》和《高层建筑混凝土结构技术规程》[8]都将抗震性能化设计引入其中,国内的新建超限建筑基本上已采用性能化设计,《高层建筑混凝土结构技术规程》把结构抗震性能目标分为四个等级,结构性能分为五个水准,地震作用分为多遇、设防、罕遇三水准。
传统观点认为采用隔震技术的建筑物和桥梁在地震中处于弹性状态,但最近地震表明隔震结构在超设计作用下,上部结构地震响应明显进入弹塑性状态,如2005年福冈县西方海域地震中,福冈市东区某隔震结构最大加速度达到112.1 cm/s2[9];仙台市宫城野区某事务所是地下 2 层、地上 18 层的钢筋混凝土结构,隔震层位于地下 1 层,该结构在 2011 年日本东北太平洋海域地震中,该结构隔震层观测到的最大位移为 230 mm,地表的最大加速度为 317 cm/s2,地上第18 层的加速度为 188.6 cm/s2[10]。上述的强震观测同时也表明隔震支座在大变形状态下会支座的第二刚度(屈服后刚度)会进入强化阶段。但目前常用的隔震支座分析模型为并未考虑其大变形强化效应。在大震作用下,支座发生大变形会出现屈服刚度硬化的现象,从而导致上部结构加速度以及隔震层剪力剧增,因此在分析隔震结构地震响应的过程中考虑支座硬化的影响是十分有必要的。
本文针对大震下隔震结构的支座刚度强化效应和上部结构弹塑性特性研究隔震结构整体弹塑性地震响应。进行铅芯橡胶隔震支座大变形力学性能试验,建立考虑隔震支座硬化效应的大变形硬化模型,并通过Perform-3D软件建立8层隔震结构模型研究隔震结构整体弹塑性地震响应。
1 铅芯橡胶支座大变形试验
1.1 试验装置及试验体
试验加载装置为竖向20 000 kN千斤顶,水平±3 000 kN电液伺服压剪试验机a,以及竖向20 000 kN千斤顶,水平±5 000 kN电液伺服压剪试验机b。图1为试验装置示意图。
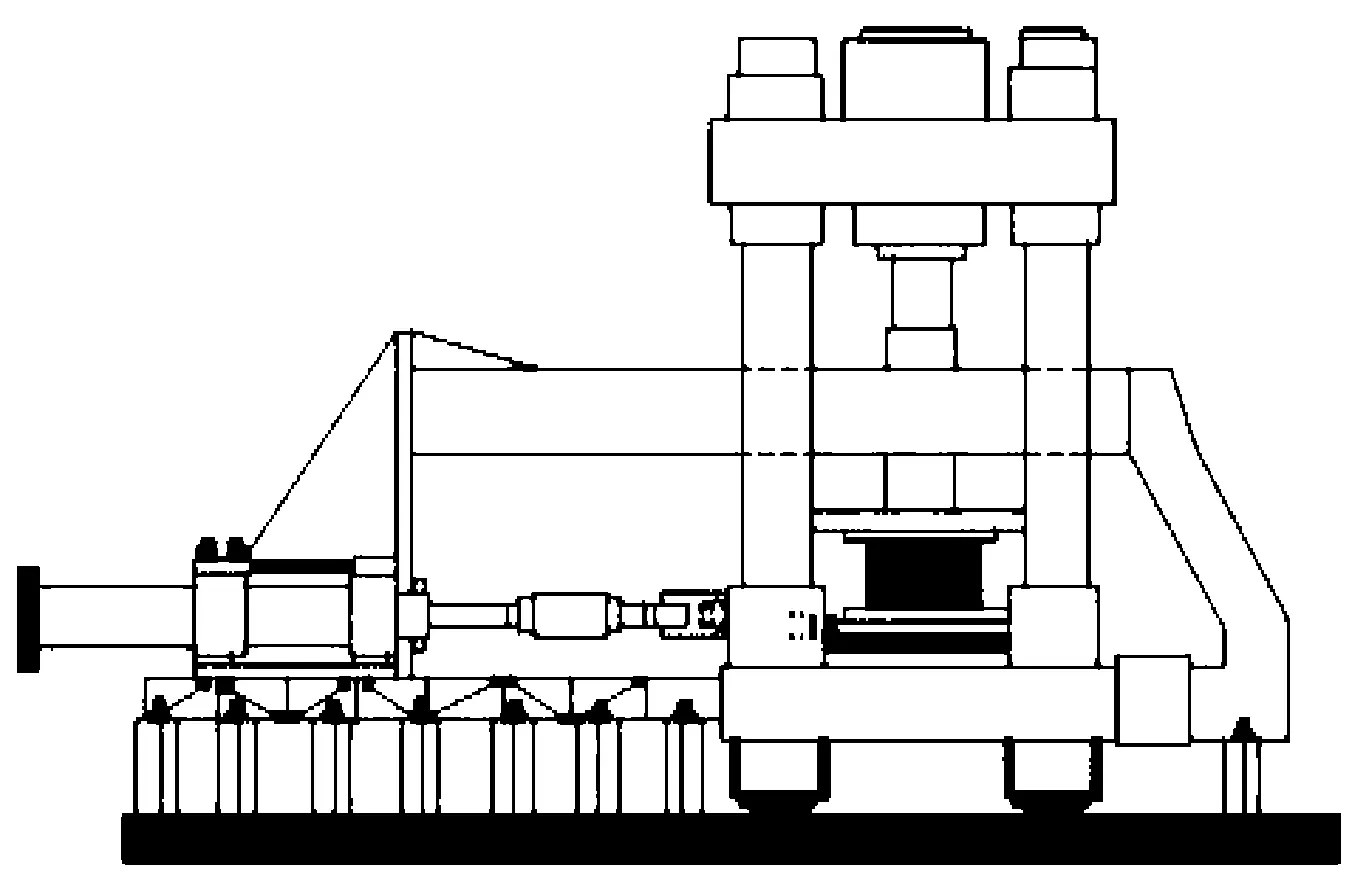
图1 压剪试验装置机构示意图
试验体由LRB600与LRB1100两组试件组成,试件的规格及参数如表1所示,为支座直径,铅芯直径,为橡胶总厚度,为第一形状系数,为第二形状系数。图2(a)为试验机a上LRB600试件γ=400%时压剪试验照片,图2(b)为试验机b上LRB1100试件在γ=300%时压剪试验照片。

表1 支座试件详细规格

(a)LRB600试件(b)LRB1100试件
图2 铅芯橡胶支座大变形压剪试验照片
Fig.2 Photos oflarge deformation experiment
试验时竖向压缩应力为5 MPa,γ(剪切应变)为水平剪切位移与橡胶总厚度比值。对于LRB600试件,进行水平剪切应变分别为γ=200%、300%和400%时的压缩剪切试验,记录隔震支座水平力和位移之间的关系。其中,γ=200%和300%时的剪切压缩试验有4次反复加载循环数据,γ=400%时,考虑到大变形试验对支座损伤的影响,因此试验做1次循环加载。试验由试验机a与试验机b各自进行,分别为试验A和试验B。对于LRB1100试件,受国内加载设备性能的限制,进行剪切应变分别为γ=100%、200%和300%时的压缩剪切试验,由试验机b进行,记为试验C。
1.2 试验结果
三组试验结果如图3所示。对于LRB600试件,γ=200%和300%时的剪切压缩试验结果取4次反复加载循环的第3次循环数据,γ=400%时取第一次循环加载数据,由于试验机b的性能限制,试验B的滞回环仅半圈。对于LRB1100试件,γ=100%、200%和300%时的剪切压缩试验结果均取4次反复加载循环的第3次循环数据。由试验结果可以看出,当铅芯橡胶支座的水平剪切变形达到约240%时,支座水平刚度明显增大,出现硬化现象,硬化刚度(三阶刚度)约为有效刚度(二阶刚度)的1.5倍。


图3 铅芯橡胶支座压剪试验结果
2 铅芯橡胶支座大变形恢复力模型
铅芯橡胶支座具有较大的阻尼,从而具有较大的滞回耗能能力。目前用于分析的铅芯橡胶支座模型主要有双线性滞回模型[11](图4(a))及Bouc-wen模型[12](图4(b)),这些模型普遍适用于低-中应变情况,对于大应变下的某些效率无法考虑,因此本文基于试验数据提出了考虑支座硬化的大变形硬化模型。
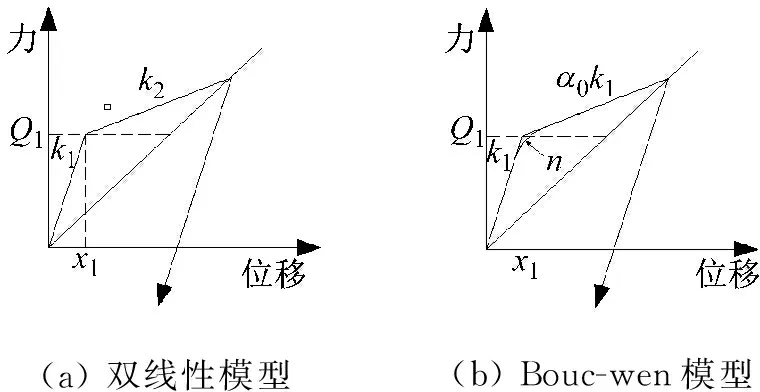
(a)双线性模型(b)Bouc-wen模型
图4 铅芯橡胶支座恢复力模型
Fig.4 Bilinear model and bouc-wen model of LRB
图4(a)中双线性模型恢复力表达式如下,式中k1为铅芯橡胶支座初始刚度,k2为屈服后刚度,Q1为屈服力:
第一阶段:
F=k1x(x≤x1)
(1)
第二阶段:
F=k2x-k2x1+Q1(x>x1)
(2)
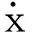
Q(t)=α0k1x(t)+(1-α0)k1x1z(t)
(3)

γ]|z(t)|n}
(4)
2.1 考虑强化效应的多线型模型
基于现有铅芯橡胶支座的双线性模型,根据LRB600与LRB1100试件水平剪切试验结果,提出一种铅芯橡胶支座考虑剪切大变形硬化效应的大变形硬化恢复力模型,如图5所示。
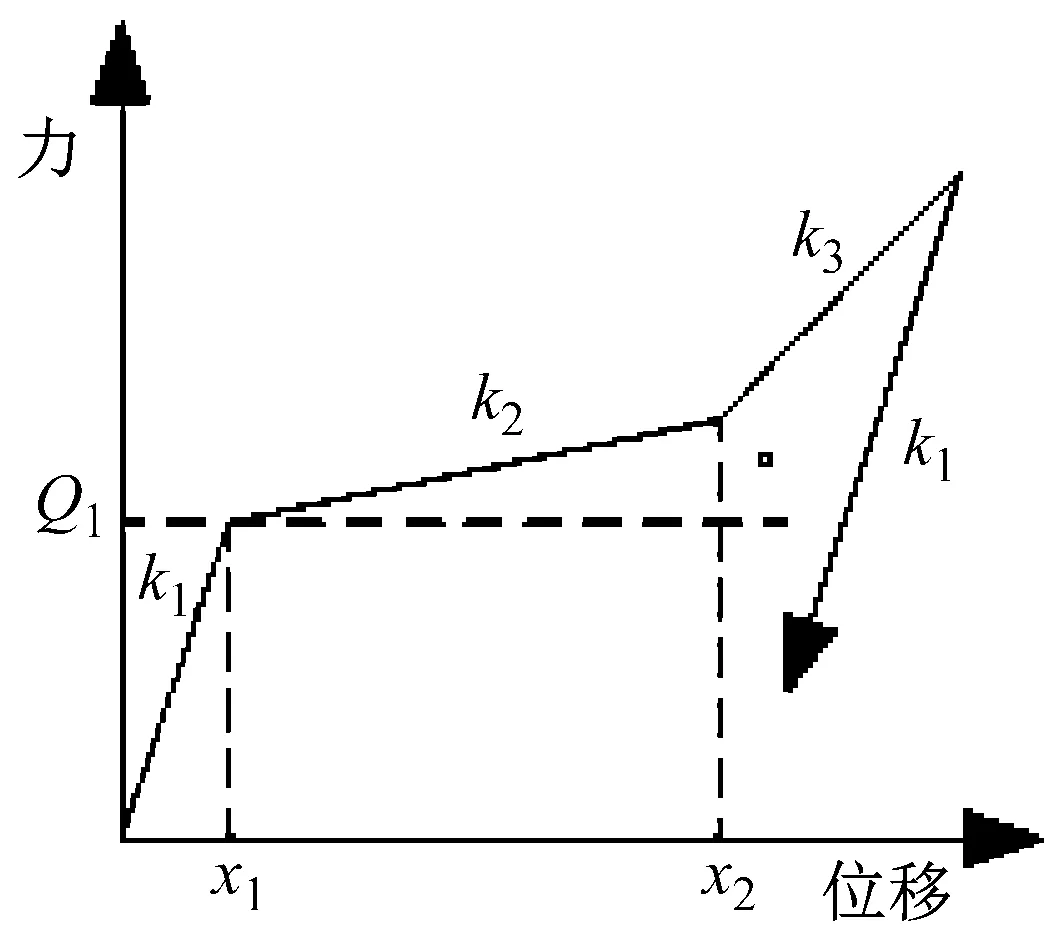
图5 铅芯橡胶支座大变形硬化模型
第一阶段:
F=k1x(x≤x1)
(5)
第二阶段:
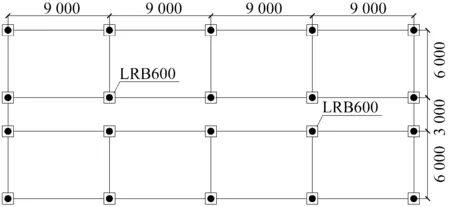
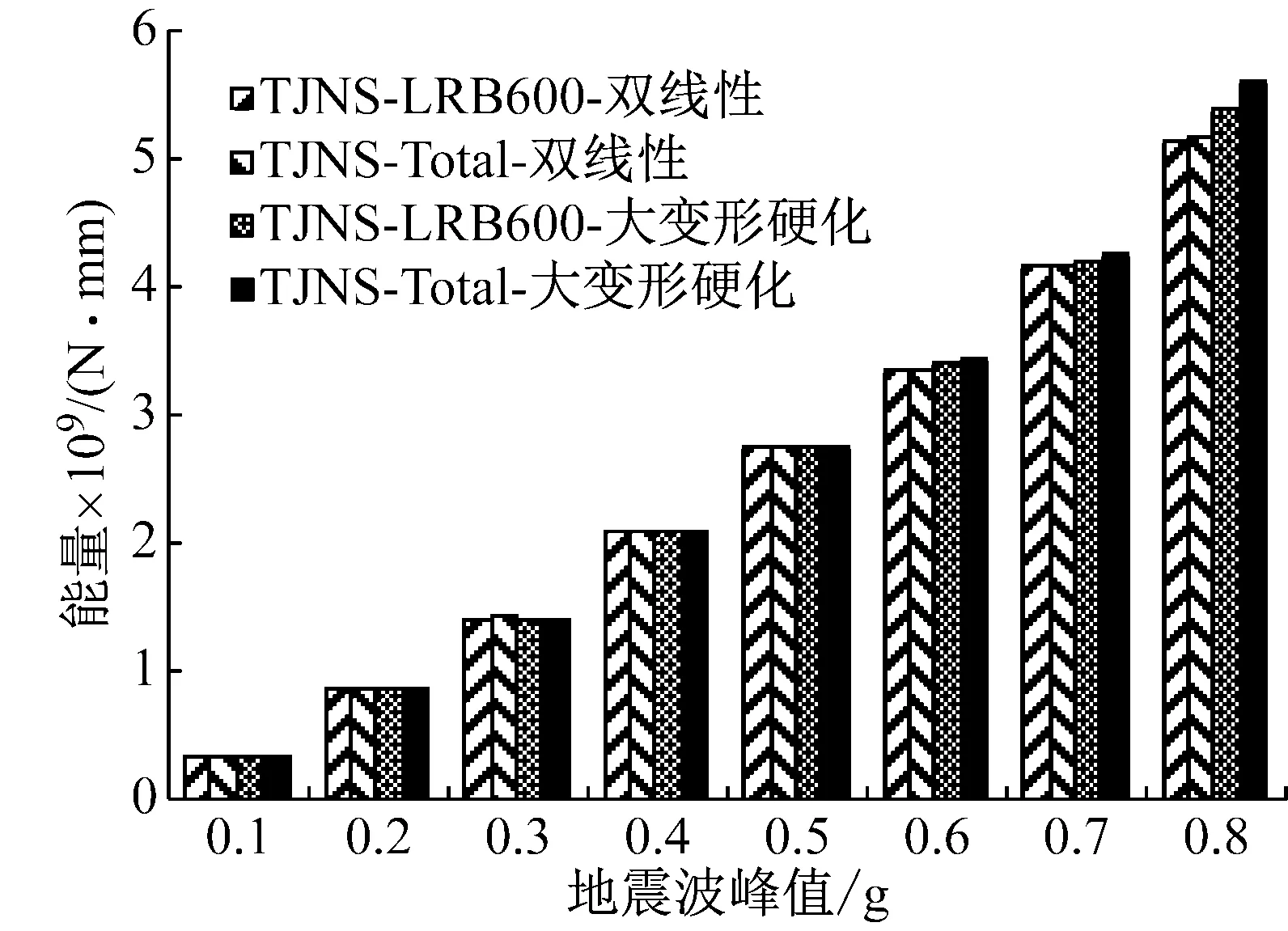
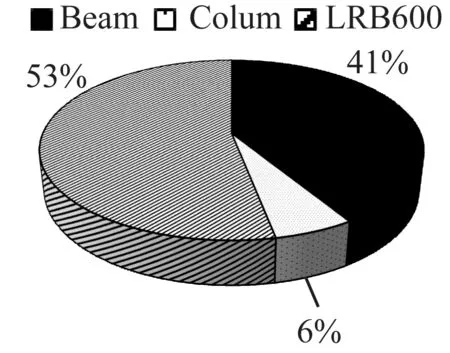
F=k2x-k2x1+Q1(x1 (6) 第三阶段: F=k3x-(k3-k2)x2-k2x1+Q1(x>x2) (7) 式中:k1为铅芯橡胶支座初始刚度;k2为屈服后刚度;k3为支座硬化后刚度;Q1为屈服力;x1为铅芯橡胶支座发生屈服时位移;x2为铅芯橡胶支座发生硬化时位移。 2.2 试验结果对比 表2为根据试验结果提出的大变形硬化模型在加载阶段各力学参数数值,支座在γ=240%时开始硬化。 图6为大变形硬化模型与试验结果对比图。铅芯橡胶试件在反复加载过程中会出现刚度退化现象,故正向加载与反向加载时会出现刚度不对称的现象,但理论值能大致吻合多组试验结果。由于LRB600试件在γ=400%时仅有一次加载数据,第一次循环时支座性能较不稳定,故试验值与理论值偏差较大,但反向加载数据仍与拟合曲线较为吻合。 表2 支座力学参数 图6 试验数据与理论公式对比 3.1 分析模型概况 为了进一步研究支座大变形强化效应对隔震结构的影响,在试验研究的基础上进一步进行通过Perform-3D软件建立8层钢筋混凝土框架隔震结构模型进行弹塑性时程分析,对隔震结构在铅芯橡胶支座发生大变形的情况下所产生的响应进行分析。隔震结构总质量为5 400 t,层高3.3 m,地面以上高度26.4 m,每层建筑面积为540 m2。隔震装置选用20个铅芯橡胶支座LRB600,支座的力学参数与试验支座一致,见表2。结构隔震前周期为0.68 s,隔震后周期为2.37 s,单个支座的实际面压为8 MPa。上部结构的梁柱采用弹塑性纤维模型,如图7所示。为了进一步研究大变形硬化效应的影响,支座模型分别采用传统的双线性模型和大变形硬化模型,后文图表对比中均简称为双线性与大变形硬化模型,支座布置图见图8。 (a) 集中纤维塑形模型 (b)梁纤维截面(c)柱纤维截面 图7 Perform-3D纤维截面示意图 Fig.7 Fiber cross section in Perform-3D 图8 隔震支座布置图(mm) 3.2 地震波及工况分析 分析采用3条实际地震波,分别为1940的El Centro-lmpValllrr地区的El Centro-180#成分波(EL Centro)、1995年神户地震时的八户波(Hachinohe)、1976年唐山地震余震天津医院记录(TJNS)。地震波峰值从0.1 g开始逐次递增至0.8 g,由此分别模拟支座采用双线性模型与大变形硬化模型的结构在不同等级地震下的响应,并进行结构的弹塑性分析研究。 3.3 地震响应结果 图9为隔震结构在不同峰值的TJNS、El-Centro、Hachinohe波作用下隔震层位移,由图可以看出当支座硬化后,大变形硬化模型由于刚度增大其层间位移小于双线性模型。对于TJNS波,支座硬化后隔震位移减小范围在10%以内;对于El-Centro波两种模型隔震层位移偏差为10%~42%,随着地震波峰值的增加,偏差越大;对于Hachinohe波,两模型偏差在50%以内。 图9 结构隔震层位移响应 图10、图11分别为隔震结构在TJNS、El-Centro、Hachinohe波作用下结构顶层的加速度与位移响应。从图中可以看出,当地震波峰值较小时,两模型计算结果一致。当TJNS、El-Centro、Hachinohe波峰值分别为0.6 g、0.5 g和0.4 g时,两种模型的计算结果开始出现偏差,说明此时支座已出现了硬化现象,且支座硬化会增大上部结构的地震响应。当地震波峰值为0.6 g时,两种模型的偏差约为28%~35%,当地震波峰值为0.7 g时,两种模型的偏差约为40%~50%,当地震波峰值为0.8 g时,两种模型的偏差约为50%~60%。由此可以看出且随着地震波峰值的增大,支座硬化后上部结构地震动响应会增大地越明显。 图10 结构顶层加速度响应 图11 结构顶层层间位移响应 上述分析表明,当地震波峰值为0.6 g时,铅芯橡胶支座已开始硬化。图12为8层隔震结构在峰值为0.6 g的TJNS、El Centro、Hachinohe波作用下上部结构层间位移。由图可以看出当地震波峰值为0.6 g时,支座硬化结构的层间位移约为支座未硬化结构的1.5倍~2倍。 图12 地震波峰值0.6 g下两种模型层间位移对比 表3为在TJNS、El Centro、Hachinohe波作用下上部结构底层的层间位移角θ。当TJNS波峰值为0.8 g时,隔震支座采用双线性模型计算的结构处于中等破坏状态,而支座采用大变形硬化模型计算的结构已进入接近倒塌状态。在El Centro波作用下,当地震波峰值为0.6 g时,双线性模型结构处于中等破坏状态,大变形硬化模型结构进入了接近倒塌状态;当地震波峰值为0.8 g时,双线性模型结构进入了接近倒塌状态,而大变形硬化模型结构已经倒塌。在Hachinohe波作用下,大变形硬化模型在地震波峰值为0.5 g时进入接近倒塌状态,双线性模型结构在地震波峰值为0.7 g时进入接近倒塌状态。以上结果表明,如果在隔震设计时不考虑支座的硬化的效应,当隔震结构遭遇中震或大震时,将存在很大的安全隐患。结构的破坏状态会比预期严重许多。图13为采用两种模型的结构在地震波峰值为0.6 g的Hachinohe波作用下,结构的塑性发展趋势图,构件的破坏程度由弱到强分别由不同符号表示。 3.4 反应谱分析 目前已有学者基于Bouc-Wen恢复力模型给出了隔震结构的弹塑性反应谱[13]。图14为当TJNS、El Centro、Hachinohe波地震波峰值为0.6 g和0.8 g时,结构分别采用大变形硬化模型与双线性模型计算得到的加速度弹塑性反应谱。由图可以看出,双线性模型的反应谱曲线值比大变形硬化模型反应谱曲线值小。当地震波峰值为0.6 g时,大变形硬化模型的反应谱峰值约为双线性模型的1倍~1.5倍;当地震波峰值为0.8 g时,大变形硬化模型的反应谱峰值约为双线性模型的2倍~3倍。以上结果表明地震波峰值为0.8 g时两种模型反应谱曲线的差异要明显大于地震波峰值为0.6 g时。在Hachinohe波作用下,加速度弹塑性反应谱曲线出现了两个峰值,在小峰值时两种模型的计算结果基本可以吻合,但在大峰值时两种模型计算结果的偏差特别大。若按照双线性模型的反应谱曲线取值会导致计算结果偏小,设计偏不安全。 表3 结构底层层间位移角θ 图13 结构塑性发展过程 (a) (b) 3.5 能量分析 图15为隔震结构的铅芯橡胶支座在TJNS、El Centro波作用下的能量柱状图。从图中可以看出,在TJNS波作用下,当地震波峰值在0.6 g以内时,铅芯橡胶支座几乎承担了结构所有的塑形耗能;当地震波峰值为0.8 g时,支座采用大变形硬化模型计算的结构大部分塑形耗能由铅芯橡胶支座承担,小部分由上部结构的塑性变形承担,而支座采用双线性模型计算的结构大部分塑形耗能仍由铅芯橡胶支座承担。在El-Centro波作用下,在地震波峰值为0.4 g时,两种模型的计算结果基本一致,铅芯橡胶支座承担结构所有的塑形能,上部结构处于弹性状态;当地震波峰值为0.6 g时,支座采用大变形硬化模型计算的结构已有小部分塑性变形由上部结构承担,当地震波峰值为0.8 g时此部分塑性变形明显增多,而支座采用双线性模型计算的结构还是大部分处于弹性状态,上部结构塑性变形非常少。 图15 两种模型支座塑性耗能对比柱状图 图16为在地震波峰值为0.6 g的Hachinohe波作用下,结构各构件塑性耗能所占百分比。由图可以看出,采用双线性模型的铅芯橡胶支座塑性耗能占整个结构塑性耗能的99%,结构其他构件塑性耗能仅占1%,表明上部结构大部分仍处于弹性状态。采用大变形硬化模型的支座塑性耗能所占比列为53%,结构的梁构件塑性耗能所占比列为41%,柱构件塑性耗能所占比列为6%,约一半的地震能量由上部结构的塑性变形承担。表明此时上部结构已经大部分进入塑性状态,结构处于非常不稳定状态。 上述分析结果表明,随着地震波能量的增大,支座硬化对上部结构的影响越明显,硬化后支座消耗的能量占整个结构塑性耗能的比重也越少。支座采用双线性模型计算的结构在小震、中震下保持着弹性状态,在大震下部分构件进入弹塑形状态。支座采用大变形硬化模型计算的结构在中震下已经部分进入弹塑性,在大震下上部结构的塑性耗能甚至超过铅芯橡胶支座,结构处于不稳定状态。如果在隔震设计时不考虑支座的硬化效应,则隔震结构会存在很大的安全隐患。 本文对铅芯橡胶隔震支座大变形硬化模型及隔震结构弹塑性地震响应进行分析研究,对比了铅芯橡胶支座采用双线性模型和大变形硬化模型时上部结构的地震响应、弹塑性反应谱以及支座耗能,主要结论如下: (1) 铅芯橡胶支座大变形试验结果表明支座水平剪切变形达到240%时,支座发生硬化,硬化刚度约为屈服刚度的1.5倍。 (2) 铅芯橡胶支座发生硬化后,隔震层水平位移减小,隔震效果减弱,上部结构的加速度与层间位移响应均明显增大。当地震波峰值为0.6 g时支座采用双线性模型与大变形硬化模型后上部结构响应偏差约为32%,当地震波峰值为0.7 g时,两模型偏差约为41%,当地震波峰值为0.8 g时,两模型偏差约为50%,随着地震波峰值的增大,两种模型的偏差会越明显。 (3) 在中震或大震情况下,支座硬化会使结构的破坏加速。支座采用大变形硬化模型的结构总是会比支座采用双线性模型的结构先一步进入下一级的破坏状态。支座硬化后,结构加速度弹塑性反应谱谱值增大,若按照双线性模型的反应谱曲线取值会导致计算结果偏小,设计偏不安全。 (4) 当地震波能量较小时,整个结构90%以上的塑性耗能由铅芯橡胶支座承担;当地震波能量较大时,硬化后铅芯橡胶支座的塑性耗能在整个结构塑性耗能中所占比重减少,上部结构构件塑性耗能所占比重增加至50%以上。相比于不考虑支座硬化的结构,支座硬化后上部结构中进入弹塑性状态的构件明显增多,结构更容易进入失稳状态。 (5) 在隔震设计时,应将铅芯橡胶支座的硬化效应考虑进去,可用本文2.1节提出的铅芯橡胶支座多线性大变形硬化模型进行隔震设计,即支座硬化点为240%,硬化后刚度为屈服刚度1.5倍。由于支座硬化后上部结构更容易进入塑形状态,因此隔震设计在考虑支座硬化的同时还应考虑上部结构弹塑性,结构中所用混凝土、钢筋等材料均采用弹塑性模型,梁柱等构件的弹塑性则可体现为在构件两端使用塑性铰或纤维截面。 [1] 建筑抗震设计规范:GB50011—2010[S].北京:中国建筑工业出版社, 2010. [2] Seismic Performance Objectives for Tall Buildings[Z]. PEER,2008. [3] ATC-40.Seismic evaluation and retrofit of concretebuildings[S]. Applied Technology Council, 1996. [4] FEMA 273.NEHRP guidelines for seismic rehabilitation of buildings[S]. Federal Emergency Management Agency, 1997. [5] FEMA 274.NEHRP commentary on the guidelines for seismic rehabilitation of buildings[S]. Federal Emergency Management Agency, 1997. [6] ASCE 41-06.Seismic Rehabilitation of Existing Buildings[S].American Society of Civil Engineers(ASCE), Reston, VA, 2006. [7] Guidelines for seismic design of tall buildings[Z]. PEER, 2010. [8] 高层建筑混凝土结构技术规程:JGJ3—2010[S]. 北京:中国建筑工业出版社, 2010. [9] MORIMOTO H. The analysis of earthquake response of isolated structure in 2005 earthquake off the west Fukuoko[C]. Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan,2005:665-666. [10] Japan National Institute for Land and Infrastructure Management[R]. The earthquake damage survey of isolated structures in Miyagi and Yamagata, 2011. [11] ROBINSON W H, TUCKER A G. Test results for lead-Rubber bearing for the William M Clayton building, Toe bridge and Waiotukupuna bridge[J]. Bull. New Zealand Nad. Soe Eng, 1983, 14(1): 21-33. [12] PARK Y J, WEN Y K, ANG H S. Random vibration of hysteretic systems under bi-directional ground motions[J]. Earthquake Engineering and Structural Dynamics, 1986, 14(4): 543-557. [13] 何文福,刘文光,杨骁. 隔震结构弹塑性反应谱分析研究[J]. 振动与冲击, 2010, 29(1):30-42. HE Wenfu, LIU Wenguang, YANG Xiao. The elastic-plastic response spectrum analysis of isolation structure[J]. Journal of Vibration and Shock, 2010, 29(1):30-42. [14] 皆川佳祐. 積層ゴムの非線形特性を考慮した免震構造の地震時挙動に関する解析的研究[M].日本機械学会論文集, 2013,79(804):2684-2693. [16] 史庆轩,王秋维,雷健. 型钢混凝土框架结构基于位移的抗震设计方法研究[J]. 建筑结构, 2009,39(7):66-70. SHI Qingxuan, WANG Qiuwei, LEI Jian. Research on displacement-based design method of steel reinforced concrete frame structures[J]. Journal of Building Structure, 2009,39(7):66-70. [17] 日本建筑协会.隔震结构设计[M].刘文光,译.北京:地震出版社,2006. Large deformation hardening model of lead rubber bearings and elastic-plastic analysis for a structure with seismic isolation WU Qianyun, HE Wenfu, LIU Wenguang, YU Weixin, QIN Chuan (Department of Civil Engineering, Shanghai University, Shanghai 200072, China) The horizontal large deformation shear tests with shear deformation 400% were conducted on LRB600 and LRB1100. It was shown that the bearings’ stiffness after yielding increases when their shear deformation reaches 240%, the hardening stiffness increases with increase in shear deformation, the hardened stiffness increases by 1.5-fold when shear deformation reaches 400%. According to the test results, a new multi-linear large deformation hardening restoring force model considering the hardening effect of LRB was proposed. This model was used in the software Perform-3D. The elastic-plastic analysis was performed on an 8-storey structure under different earthquake intensities, the traditional bilinear model and the proposed multi-linear one were adopted, respectively for LRBs to comparatively analyze the structure’s seismic responses, elastic-plastic response spectra and plastic energy-dissipation states. The results indicated that the bearing hardening can weaken the seismic isolation effect of LRBs under the major earthquake, the acceleration of the upper structure increases by 30%~50%, the structure’s plastic energy-dissipation increases, the upper structure enters the plastic deformation status; so, the seismic response of the structure may be underestimated without considering the bearing hardening effect in the seismic isolation design. lead rubber bearing (LRB); bearing hardening; seismic response; response spectrum; energy 国家自然科学基金(51308331;51278291) 2015-12-24 修改稿收到日期:2016-06-16 吴倩芸 女,硕士,1993年9月生 何文福 男,博士,讲师,1979年生 TH212;TH213.3 A 10.13465/j.cnki.jvs.2017.15.014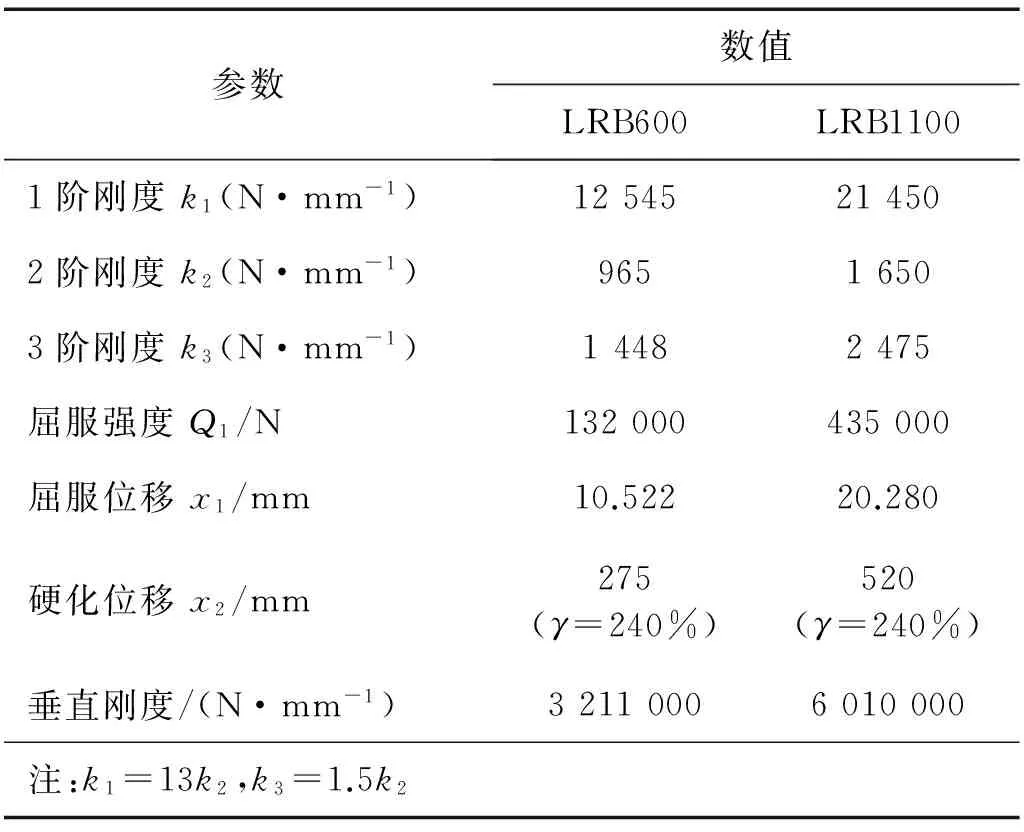


3 考虑上部结构弹塑性和支座强化效应地震响应分析











4 结 论


