多快递员的电商物流“最后一公里”配送研究
袁雨果
多快递员的电商物流“最后一公里”配送研究
袁雨果
(集美大学 诚毅学院 商船系, 福建 厦门 361021)
物流配送是支撑电子商务发展的关键环节和重要基础。作为电商物流的最后环节——“最后一公里”配送,更是直接影响客户对电商的满意度。以电商物流“最后一公里”配送为对象,研究多快递员任务分配和线路优化。将其抽象为一个考虑任务均衡的多旅行商问题,并设计改进遗传算法进行求解。为验证算法性能,通过构建算例对比改进遗传算法和一般遗传算法的效果差异。独立样本t检验结果表明,改进遗传算法能够获得更好效果。
“最后一公里”配送;任务均衡;多旅行商;遗传算法
一、引言
随着互联网技术的发展和普及,近年来我国电子商务得到了迅猛发展,特别是B2C和C2C型电子商务更是呈现井喷式发展,占据了电子商务交易的主要份额,涌现了一批如淘宝网、京东商城等一批代表性企业。电子商务的发展也带动了物流配送需求的快速增长[1]。根据《2015年度快递市场监管报告》,全国快递服务企业业务量累积完成206.7亿件,其中6成来自于电子商务业务,电子商务已经成为我国快递业持续快速发展的重要推动力量。另一方面,物流配送也是支撑电子商务发展的关键环节和重要基础[2,3],物流配送质量的高低直接影响客户对电商企业的满意程度[4,5]。
物流配送的基本流程包括仓储阶段、主干网运输阶段和“最后一公里”配送阶段。与一般物流配送不同,电子商务物流“最后一公里”配送具有对配送方式要求苛刻、对配送时效要求很高、个性化差异化配送需求多、订单数量大规模小等特点,因此面临众多问题或挑战[6]。《2015年度快递市场监管报告》指出,2015年我国快递服务满意度仅为74分,72小时准时率仅为73.85%,有效申诉率为13.3件/百万件(27.56万),其中因投递服务和延误导致的申诉分别有10.37万件和8.62万件,分别占比37.6%和31.3%。因此,作为物流配送终端环节的“最后一公里”成为制约配送效率、影响服务质量的关键[7,8]。
本文正是在这样的背景下,以物流配送“最后一公里”为研究对象,研究多快递员任务分配和线路优化问题。在该问题中可以分为两个阶段:第一个阶段是将快递配送任务分配给不同快递员;第二阶段是根据任务配送的位置,为快递员规划线路。这个问题可以抽象为一个多旅行商问题(Multiple TravelingSalesman Problem)。过去有很多研究对这个问题展开研究,然而却往往忽略了任务分配均衡性的问题,从而会导致有些快递员超负荷运行,而有些快递员却处于空闲状态。因此,在优化多快递员任务分配和线路优化时需要将快递员间的任务均衡性纳入考虑范畴。多旅行商问题已经被证明是一个NP难问题,很难通过精确算法对大规模多旅行商问题进行精确求解。因此本文提出了一个改进遗传算法,包括了染色体编码等4个步骤。为了验证该算法的性能,本文构建了一个算例,并引入一般遗传算法为对比。通过独立样本t检验的结果表明,把问题提出的改进遗传算法比一般遗传算法具有更好的优化效果。
二、文献综述
(一)“最后一公里”配送
电子商务物流是指电子商务物流服务提供者采用网络化的计算机技术和现代化的硬件设备、软件系统以及先进的管理手段,针对客户的需求、根据客户的订货要求,进行一系列的分类、编码、整理配货等理货工作,按照约定的时间和地点将指定数量和规格要求的商品传递到用户的活动和过程。它的基本流程包括仓储、主干网运输和“最后一公里”配送等3个阶段[6]。其中,“最后一公里”配送是电子商务物品从物流仓储中心发送至目的地的过程,它是完成电子商务交易的最后一个环节[9]。与一般物流配送不同,电子商务物流“最后一公里”配送具有对配送方式要求苛刻、对配送时效要求很高、个性化差异化配送需求多、订单数量大规模小等特点,因此面临众多问题或挑战[6]。
现阶段电子商务物流“最后一公里”配送的模式不断丰富,包括送货上门、自助收发箱和顾客自提站等模式[10]。针对送货上门的研究主要集中于优化配送线路、降低配送成本和提升顾客满意度等方面。而对于自助收发箱,Mikko等人等人通过仿真研究表明采用自主收发箱模式可以比标准的送货上门的模式节约60%的成本[11]。而客户自提站模式也是解决最后一公里配送的有效方法,选择什么样的机构作为自提点的合作伙伴将对“最后一公里”配送的成本、效率产生很大的影响[12]。方玺和耿艳探讨了我国“最后一公里”各种配送方式的优劣,并提出了创新派送模式的建议[13]。
不管“最后一公里”配送采用哪种方式,都需要解决由哪个快递员配送、按什么样的顺序配送等问题。可以将该问题抽象为一个具有多个旅行商的配送问题。
(二)多旅行商问题
多旅行商问题 (Multiple Traveling Salesman Problem,MTSP)是旅行商问题的更为一般化的形式,它需要为多个旅行商规划线路。相比旅行商问题,对于多旅行商问题的研究还相对较少,但多旅行商问题却具有更加重要的实践意义,很多实际的问题都常常为转换为多旅行商问题并加以求解[14],比如人力资源规划[15-18]、交通规划[19,20]、任务分配[21]、生产调度[22]、出版印刷调度[23,24]等。
关于MTSP问题的求解,有学者尝试从运用精确算法进行求解,比如:Ali和Kennington提出了一个基于分支定界的方法来解决不对称MTSP问题,但是他们研究的问题规模相对较小[25];而Gavish and Srikanth则尝试用该方法解决一个更大规模的对称性MTSP问题[26],相比过去研究,他们的算法得到明显提升。
Gromicho等人则基于准分配算法 (quasiassignment) 的精确算法去解决不对称的MTSP[27]。然而,Tang和Denardo指出MTSP是一个典型NP难问题[28],很难在有限的时间内对大规模问题进行精确求解。因此,越来越多的学者致力于设计出各种启发式算法对多旅行商问题进行求解,比如神经网络[29,30]、遗传算法[22,31,32]、禁忌搜索算法[33]、蚁群算法[34]、模拟退火方法[35],Sofge等人则比较了多种解决MTSP的进化算法,包括粒子群算法、蒙特卡洛优化算法等[36]。
通常情况下,多旅行商问题的主要目标是所有旅行商旅行距离/成本/时间的最小化,然而这往往会导致旅行商之间任务的不均衡[37]。因此,有学者指出限制单个旅行商的路程具有一定的实际意义,因此他们将目标函数定义为所有旅行商路程最大值的最小化[38,39]。本文基于这样的背景下,在构建多旅行问题模型时充分考虑了快递员之间的任务均衡。
三、数学模型构建
对于电子商务“最后一公里”配送问题,可以将其抽象为具有单个物流仓储中心,M个快递员和N个配送地址的多旅行商问题。配送地址可以是客户的地址,也可以是自助收发箱或顾客自提站。本文将相同配送地址的所有快递均视为同一任务。每个快递员都从物流仓储中心出发,完成所有配送任务以后又回到仓储中心。问题的目标是使得所有快递员的配送时间最短。在传统的多旅行商问题求解中,由于过分追求最配送时间最短,会出现快递员之间配送任务不均衡的情况[37]。因此,本文为了确保快递员的工作量相对均衡,引入了均衡系数δ。具体建模过程如下:
设物流仓储中心为v0,每个任务的配送地址标记为v1,v2,…,vN。快递员的个数为M。变量,当快递员k经过弧段(vi,vj) (即配送完任务vi后又相继配送订单v)j,则否则yki也为0-1变量,当位于vi的任务分配给第k个快递员时,则有yki=1,否则yki=0。cij表示快递员经过对应弧段(vi,vj) 的时间距离。则目标函数如式(1)所示,表示所有快递员配送时长之和最小。其中zk表示第k个快递员的配送时长。式(3)-(7)表示问题的约束条件:式(3)表示从物流配送中心出发,所有订单只有一个快递员配送;式(4)表示任一条弧的终点位置仅有一个起点位置与之相连;式(5)表示任一条弧的起点位置仅有一个终点位置与之相连;式(6)表示任务均衡要求;式(7)表示消去构成不完整线路的解,其中S为支路消去约束,即消去构成不完整路线的解[40]。

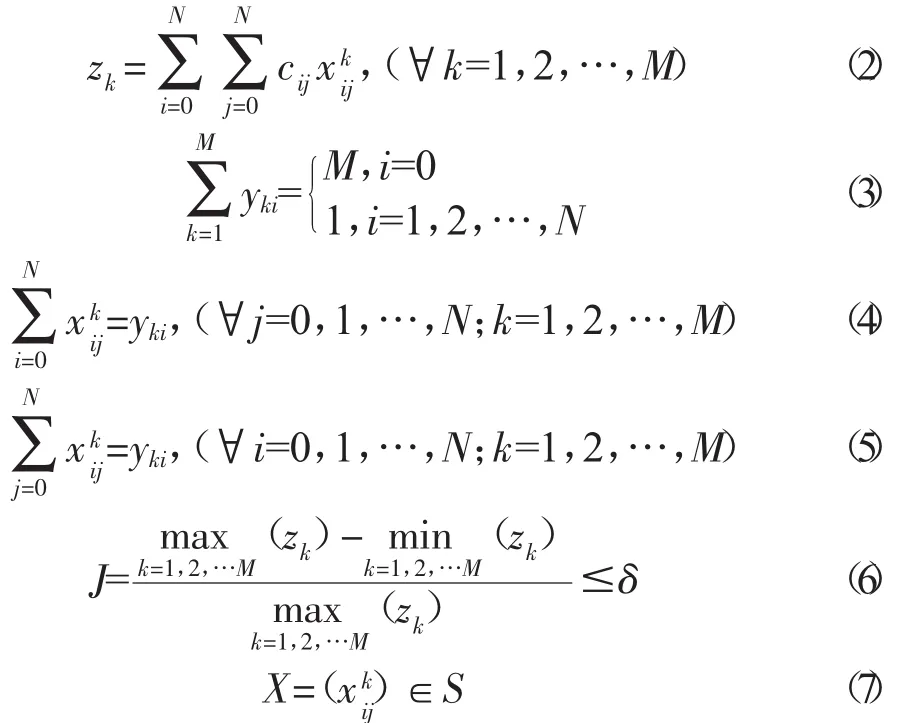
四、改进遗传算法
MTSP问题是一个NP难问题,很难在有限的时间内通过一个多项式算法求解其精确值。因此,本文通过设计一个改进遗传算法对上述算法进行求解,其算法流程图如图1所示,包括了染色体编码、初始解集合构造、解集合进化和解集合评估等4个主要步骤。
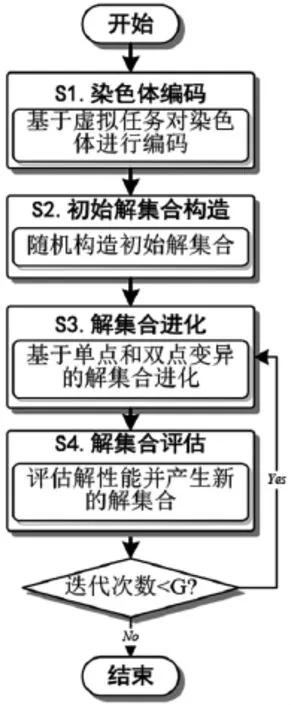
图1 算法流程图
(一)染色体编码
沿用上面变量定义,即快递员数量为M,需配送的任务地址数量为N。本文通过引入虚拟任务地址来进行染色体编码,具体处理如下:引入M-1个虚拟任务地址,则该问题可以转换为单旅行商问题,即一个快递员从仓储中心v0出发,完成所有任务的配送后,又回到v0。则只需要对{v1,…,vN,vN+1,…,vN+M-1}进行随机排列,即可得到其中一条染色体。为了说明编码的过程,以具有10个任务,3名快递员的情况为例。需要引入2个虚拟任务,分别标记为v11和v12。则对{v1,v2,…,v10,v11,v12}这12个任务随机排序,假定得到其中的一条染色体为0-1-5-7-9-11-10-8-2-12-3-4-6-0。将染色体中的虚拟位置替换为仓储中心 v0,即可得到0-1-5-7-9-0-10-8-2-0-3-4-6-0。以“0”为标记将该染色体进行拆分,得到{0-1-5-7-9-0},{0-10-8-2-0}和{0-3-4-6-0}等3条子染色体,即表示3名快递员所分配的配送任务及任务配送线路。
(二)初始解集合构造
根据上述方式,对{v1,…,vN,vN+1,…,vN+M-1}进行随机排列,理论上可以有!种排列方式。但是并不是所有的解都是可行解。需要根据上述的约束条件对随机产生的解进行甄别,只有满足所有约束条件的染色体才可以视为可行解,并进入初始解集合。初始解产生的流程如下:
(1)引入M-1个虚拟任务,构建任务集合{v1,…,vN,vN+1,…,vN+M-1};
(2)根据任务集合,随机产生一条染色体;
(3)拆分染色体以确定每名快递员的配送任务及任务配送线路;
(4)计算每名快递员完成所有配送任务需要的时长zk;
(5)如果满足均衡度要求,即符合式(6)的任务均衡约束,则该染色体记为可行解,将其插入到初始解集合IS中,否则重新返回步骤(2);
(6)如果初始解集合IS所包括的可行解数量达到种群规模Q,则结束初始解集合构造过程,否则返回步骤(2)。
(三)解集合进化
传统的遗传算法通常会采用交叉互换、变异和复制等算子。考虑到本文染色体的特殊性,本文在进行解进化时,只采用了单点变异和双点变异两种算子。为了更好地说明这两种算子,分别以图2和图3来说明变异的过程。
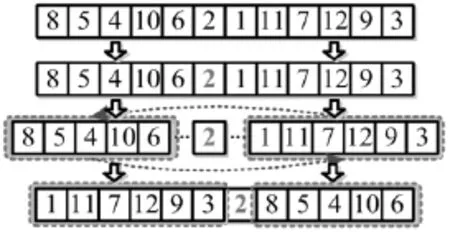
图2 单点交叉变异
对于单点变异,首先从解集合中任意选择一个解(如8-5-4-10-6-2-1-11-7-12-9-3),并从中任意选择一个基因(如图2标红的“2”)。以该变异点为 节 点 , 将 染 色 体 截 取 为 8-5-4-10-6和1-11-7-12-9-3两个染色体片段,并将这两个染色体片段互换位置,进而得到新的染色体,即:1-11-7-12-9-3-2-8-5-4-10-6。
同样地,以图3为例说明染色体双点变异的过程。同样从解集合中随机选择一条染色体(如1-11-7-12-9-3-2-8-5-4-10-6),并在选取的染色体中随机选择两个基因(如图3的“7”和“5”)。以两个变异基金为节点,可以将染色体截取为1-11,12-9-3-2-8和4-10-6等3个子染色体片段。将两个变异基因之间的染色体片段进行倒序排序,得到新的染色体,即1-11-7-8-2-3-9-12-5-4-10 -6.
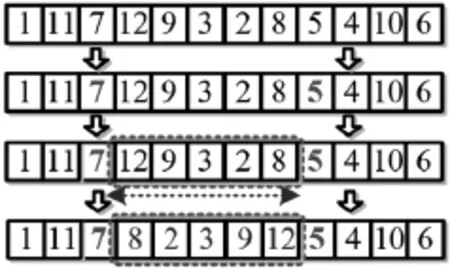
图3 两点交叉变异
(四)解集合评估
将进化后的所有解进行评估,首先还是删除掉不可行解,包括具有重复配送和没有配送到的解,以及删除掉不满足任务均衡条件的解。之后根据目标函数Eq.(1)进行评价。得到最好的Q条染色体再进入新的一次迭代,直至达到最大迭代次数。将最后的解集合中性能最好的染色体即为最满意解,作为算法的输出。
五、算例分析及讨论
为了说明本算法的性能,通过构建一个算例来对比改进遗传算法 (Improved Genetic Algorithm,IGA)的效果。绿色方块为唯一的仓储物流中心,并随机产生50个订单,其位置随机分布在仓储物流中心的四周(如图4红色圆圈所示),另外产生4名快递员。此外,本文引入了标准遗传算法(Standard Genetic Algorithm,SGA)作为对比。分别用IGA和SGA对该算例运行100次,并运用独立样本t检验对两种方法运行的结果进行比较分析。在算法运行前,需要对输入参数进行设定,将均衡度δ设定为0.5,种群规模为200。
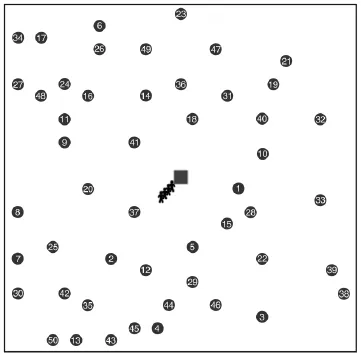
图4
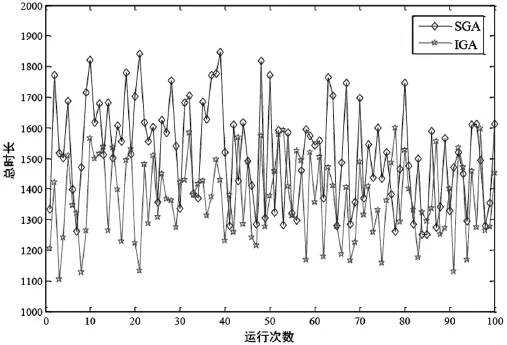
图5 SGA和IGA优化效果对比(100次)
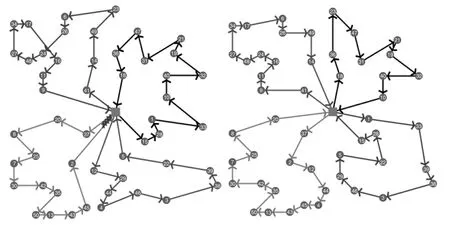
图6 SGA和IGA优化效果对比图

表1 两种方法优化结果的描述统计
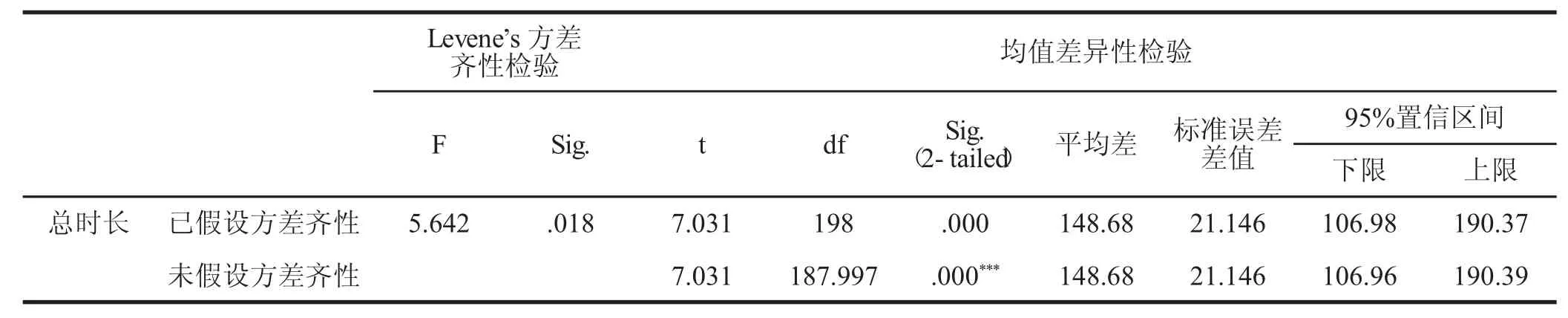
表2 两种方法优化结果的独立样本T检验结果
两种方法运行的结果如图5所示,其中蓝色曲线表示SGA所优化的结果,而红色曲线表示IGA所优化的结果。图6(左)展示了运行SGA100次中效果最优方案,在这个优化方案中,每个快递员的线路分别为:[15 28 1 33 10 40 32 19 21 31 47 36 18]、 [41 14 49 23 6 26 24 48 27 34 17 16 11 9]、[37 20 8 25 7 30 42 35 50 13 43 45 2]和[12 29 44 4 46 3 38 39 22 5];而图6(右)则展示了运行IGA100次中效果最优的方案,在这种优化方案中,每个快递员的线路分别为:[18 36 23 47 31 21 19 32 40 10]、[1 33 39 38 3 46 29 5 22 28 15]、[37 2 12 44 4 45 43 13 50 35 42 30 7 25 8 20]和[41 9 11 16 24 48 27 34 17 6 26 49 14]。
为了进一步比较两种方法的差异,本文运用独立样本t检验的方法对两种方法得到的结果进行进一步的分析对比。两种方法优化的结果如表1所示,而通过独立样本t检验发现IGA得到的结果(均值=1371.04,标准差=131.15)显著优于(均值=1519. 72,标准差=165.87) (t(100)=7.031,P<0.05),如表2所示,此外,IGA的稳定性也要高于SGA(131.15<165.87)。
六、研究总结与展望
近年来,我国电子商务的迅猛发展带动了物流配送需求的快速增长。而另一方面,物流配送也是支撑电子商务发展的关键环节和重要基础。特别是作为“最后一公里”的物流配送,更是直接影响客户对电商的满意度。与一般物流配送不同,电子商务物流的“最后一公里”配送具有对配送方式要求苛刻、对配送时效要求很高、个性化差异化配送需求多、订单数量大规模小等特点,因此面临众多问题或挑战。
本文以电子商务物流“最后一公里”配送为研究对象,研究多快递员任务分配和线路优化。将该问题抽象为一个考虑任务均衡的多旅行商问题,并设计了一个改进遗传算法对其进行求解。该算法包括染色体编码、初始解集合构造、解集合进化和解集合评估等4个步骤。其中在染色体编码中,本文引入了虚拟任务,从而优化了染色体的编码方式;在解集合进化中,与一般遗传算法通过交叉互换、变异和复制等算子进行进化不同,本文主要采用单点和双点变异的算子。为了验证算法的性能,构建了一个算例来比较改进遗传算法和一般遗传算法的效果。独立样本t检验的结果表明,改进遗传算法确实能够获得更好的优化方案。
本文所提出的改进遗传算法尽管能够较好地解决考虑任务均衡的多旅行商问题,但是随着任务规模的增加,算法的效率还有待提升。此外,在电子商务物流“最后一公里”配送中,特别是对于送货上门这种配送方式,经常会出现客户具有严格的配送时间窗口的问题,同时在配送过程中也会出现等待客户、运输时间不确定等随机问题。因此,在今后的研究中需要考虑配送时间窗口和随机性的问题。
[1]符瑛,彭银香.电子商务环境下物流配送模式选择[J].中国管理信息化,2009,12(19):115-117.
[2]杨朋珏,胡昊,王俊嘉,等.电子商务环境下城市配送末端网点选址模型研究[J].工业工程与管理,2014,19(1):35-40.
[3]张成志,赵亮.电子商务下的物流配送模式选择研究[J].物流技术,2012,31(19):66-68.
[4]崔珊珊,陈宏,俆加胜.电商促销井喷需求下的应急商品配送研究[J].中国管理科学,2013,(s1):141-147.
[5]Holdorf S,Haasis H-D.Last mile delivery concepts in E-Commerce an empirical approach[A].,2014 8th IEEE International Conference on Software,Knowledge,Information Management and Applications(SKIMA)[C].2014:1-6.
[6]杨聚平.以客户为中心“最后一公里”配送模式研究[D].北京:对外经济贸易大学,2014.
[7]詹斌,谷孜琪,李阳.“互联网+”背景下电商物流“最后一公里”配送模式优化研究[J].物流技术,2016,35(1):1-4.
[8]张锦,陈义友.物流“最后一公里”问题研究综述[J].中国流通经济,2015,(4):23-32.
[9]Lee HL,Whang S.Winning the last mile of e-commerce[J].MIT Sloan Management Review,2001,42(4):54-62.
[10]詹林敏.电子商务物流最后一公里配送模式研究[D].大连:大连理工大学,2015.
[11]Punakivi M,Holmstr.m J,Yrj.l.H.Solving the last mile issue:reception box or delivery box?[J].International Journal of Physical Distribution &Logistics Management,2001,31(6):427-439.
[12]Song L,Cherrett T,Mcleod F,等.Addressing the last mile problemthe transport impacts of collection/delivery points[J].Transportation Research Record Journal of the Transportation Research Board,2009,2097(2097):9-18.
[13]方玺,耿艳.我国快递“最后一公里”收派模式创新探讨[C].中国论坛论文集,2012,5-5.
[14]Bektas T.The multiple traveling salesman problem:an overview of formulations and solution procedures[J].Omega,2006,34(3):209-219.
[15]Svestka JA,Huckfeldt VE.Computational experience with an msalesman traveling salesman algorithm [J].ManagementScience,1973,19(7):790-799.
[16]Gilbert KC,Hofstra RB.A new multiperiod multiple traveling salesman problem with heuristic and application to a scheduling problem[J]. Decision Sciences,1992,23(1):250-259.
[17]Okonjo-Adigwe C.An effective method of balancing the workload amongst salesmen[J].Omega,1988,16(2):159-163.
[18]Calvo RW,Cordone R.A heuristic approach to the overnight security service problem[J].Computers&Operations Research,2003,30(9):1269-1287.
[19]Angel R,Caudle W,Noonan R,等.Computer-assisted school bus scheduling[J].Management Science,1972,18(6):279-288.
[20]Kim KH,Park Y-M.A crane scheduling method for port container terminals[J].European Journal of operational research,2004,156(3):752-768.
[21]Basu A,ElnagarA,Al-HajjR.Efficientcoordinated motion[J]. Mathematical and computer modelling,2000,31(2-3):39-53.
[22]Tang L,Liu J,Rong A,等.A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron&Steel Complex☆ [J].European Journal of Operational Research,2000,124(2):267-282.
[23]Gorenstein S.Printing press scheduling for multi-edition periodicals[J]. Management Science,1970,16(6):373-383.
[24]Carter AE, Ragsdale CT.Scheduling pre-printed newspaper advertising inserts using genetic algorithms[J].Omega,2002,30(6):415-421.
[25]Ali AI,Kennington JL.The asymmetric M-travelling salesmen problem:A duality based branch-and-bound algorithm[J].Discrete Applied Mathematics,1986,13(2-3):259-276.
[26]Gavish B,Srikanth K.An optimal solution method for large-scale multiple traveling salesmen problems[J].Operations Research,1986,34(5):698-717.
[27]Gromicho J,Paix.o J,Bronco I.Exact solution of multiple traveling salesman problems.Combinatorial Optimization:Springer,1992:291-292.
[28]Tang CS,Denardo EV.Models arising from a flexible manufacturing machine,part I:minimization of the number of tool switches[J]. Operations research,1988,36(5):767-777.
[29]Somhom S,Modares A,Enkawa T.Competition-based neural network for the multiple travelling salesmen problem with minmax objective[J]. Computers&Operations Research,1999,26(4):395-407.
[30]Torki A,Somhon S,Enkawa T.A competitive neural network algorithm for solving vehicle routing problem [J].Computers& Industrial Engineering,1997,33(3):473-476.
[31]Carter AE,Ragsdale CT.A new approach to solving the multiple traveling salesperson problem using genetic algorithms[J].European Journal of Operational Research,2006,175(1):246-257.
[32]Yuan S,Skinner B,Huang S,等.A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms[J]. European Journal of Operational Research,2013,228(1):72-82.
[33]Ryan JL,Bailey TG,Moore JT,等.Reactive tabu search in unmanned aerialreconnaissance simulations [A].Proceedings ofthe 30th conference on Winter simulation[C].IEEE Computer Society Press,1998:873-880.
[34]Pan J,Wang D.An Ant Colony Optimization Algorithm for Multiple Travelling Salesman Problem [A].InternationalConference on Innovative Computing,Information and Control[C].2006:210-213.
[35]Song C-H,Lee K,Lee WD.Extended simulated annealing for augmented TSP and multi-salesmen TSP[A].2003 IEEE Proceedings of the International Joint Conference on Neural Networks[C].2003:2340-2343.
[36]Sofge D,Schultz A,De Jong K.Evolutionary computational approaches to solving the multiple traveling salesman problem using a neighborhood attractor schema [A].Workshops on Applications of Evolutionary Computation[C]:Springer,2002:153-162.
[37]Alves RM,Lopes CR.Using genetic algorithmstominimizethe distance and balance the routes for the multiple traveling salesman problem[A].2015 IEEE Congress on Evolutionary Computation(CEC)[C].2015:3171-3178.
[38]周辉仁,唐万生,王海龙.基于差分进化算法的多旅行商问题优化[J].系统工程理论与实践,2010,30(8):1471-1476.
[39]周辉仁,唐万生,魏颖辉.基于GA的最小旅行时间的多旅行商问题研究[J].计算机应用研究,2009,26(7):2526-2529.
[40]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.
Study on Last Mile Delivery of Multi-Couriers E-logistics
YUAN Yu-guo
(Chengyi University College,Jimei University,Xiamen,Fujian 361021)
The logistics is the important back-up and basis for the development of E-commerce.Especially,the Last Mile Delivery,which serves as the last part of the E-logistics,is directly affect the customer satisfaction.This paper focuses on the Last Mile Delivery,and studies the task assignment and route optimization for the multiple couriers.This issue can be abstracted as a multiple travelling problem with consideration of task balancing.An improved genetic algorithm is proposed to solve the MTSP.In order to evaluate the performance of the proposed algorithm,an instance is constructed,and the basic genetic algorithm is used as baseline.The results of an independent samples t-test indicate that the proposed method indeed performs significantly better than the basic genetic algorithm.
last mile delivery;task balancing;MTSP;genetic algorithm
C931
A
1671-9743(2017)07-0039-06
2017-05-21
袁雨果,1989年生,女,陕西汉中人,助教,研究方向:物流管理、旅游供应链管理。

